Cours MIT "Sécurité des systèmes informatiques". Conférence 16: «Side Channel Attacks», partie 3

Institut de technologie du Massachusetts. Cours magistral # 6.858. "Sécurité des systèmes informatiques." Nikolai Zeldovich, James Mickens. 2014 année

Computer Systems Security est un cours sur le développement et la mise en œuvre de systèmes informatiques sécurisés. Les conférences couvrent les modèles de menace, les attaques qui compromettent la sécurité et les techniques de sécurité basées sur des travaux scientifiques récents. Les sujets incluent la sécurité du système d'exploitation (OS), les fonctionnalités, la gestion du flux d'informations, la sécurité des langues, les protocoles réseau, la sécurité matérielle et la sécurité des applications Web.

Cours 1: «Introduction: modèles de menace» Partie 1 / Partie 2 / Partie 3
Conférence 2: «Contrôle des attaques de pirates» Partie 1 / Partie 2 / Partie 3
Conférence 3: «Débordements de tampon: exploits et protection» Partie 1 / Partie 2 / Partie 3
Conférence 4: «Séparation des privilèges» Partie 1 / Partie 2 / Partie 3
Conférence 5: «D'où viennent les systèmes de sécurité?» Partie 1 / Partie 2
Conférence 6: «Opportunités» Partie 1 / Partie 2 / Partie 3
Conférence 7: «Native Client Sandbox» Partie 1 / Partie 2 / Partie 3
Conférence 8: «Modèle de sécurité réseau» Partie 1 / Partie 2 / Partie 3
Conférence 9: «Sécurité des applications Web», partie 1 / partie 2 / partie 3
Conférence 10: «Exécution symbolique» Partie 1 / Partie 2 / Partie 3
Conférence 11: «Ur / Web Programming Language» Partie 1 / Partie 2 / Partie 3
Conférence 12: Sécurité du réseau, partie 1 / partie 2 / partie 3
Conférence 13: «Protocoles réseau», partie 1 / partie 2 / partie 3
Conférence 14: «SSL et HTTPS» Partie 1 / Partie 2 / Partie 3
Conférence 15: «Logiciel médical» Partie 1 / Partie 2 / Partie 3
Conférence 16: «Side Channel Attacks» Partie 1 / Partie 2 / Partie 3

Public: Utilisez-vous la méthode Karatsuba?

Professeur: oui, c'est une méthode de multiplication intelligente qui ne nécessite pas quatre étapes de calcul. La méthode Karatsuba est enseignée dans le cours .601, ou comment est-elle désignée aujourd'hui?

Audience: 042.

Professeur: 042, excellent. Oui, c'est une très bonne méthode. Presque toutes les bibliothèques cryptographiques l'utilisent. Pour ceux d'entre vous qui ne sont pas diplômés de notre institut - je dis cela parce que nous avons des étudiants diplômés ici - j'écrirai sur la méthode Karatsuba au tableau. Ici, vous devez calculer trois valeurs:

a ₁ b ₁
(a ₁ - a ₀ ) (b ₁ - b ₀ )
a ₀ b ₀

Ainsi, vous effectuez 3 multiplications au lieu de quatre, et il s'avère que vous pouvez restaurer cette valeur a ₁ b ₀ + a ₀ b _{1 à} partir de ces trois résultats de multiplication.



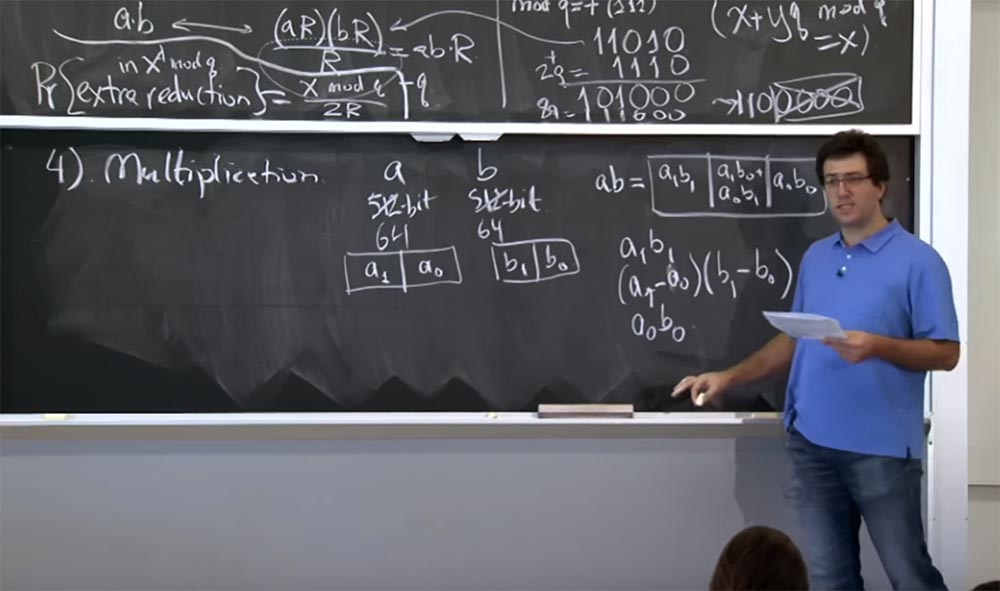
La façon spéciale de le faire est la suivante ... laissez-moi le mettre sous une forme différente.

Nous aurons donc:

(2 ⁶⁴ + 2 ³² ) (a ₁ b ₁ ) +
(2 ³² ) (- (a ₁ - a ₀ ) (b ₁ - b ₀ )
(2 ³² + 1) (a ₀ b ₀ )

Ce n'est pas très clair, mais si vous travaillez sur les détails, finissez par vous convaincre que cette valeur dans ces 3 lignes est équivalente à la valeur de ab, mais en même temps réduit le calcul par une multiplication. Et la façon dont nous appliquons cela à des multiplications plus volumineuses est que vous continuez à descendre récursivement. Donc, si vous avez des valeurs de 512 bits, vous pouvez les diviser en multiplication de 256 bits. Vous effectuez trois multiplications de 256 bits, à chaque fois récursivement en utilisant la méthode Karatsuba. Au final, vos calculs se résument à la taille de la machine et peuvent être traités par une seule instruction machine.



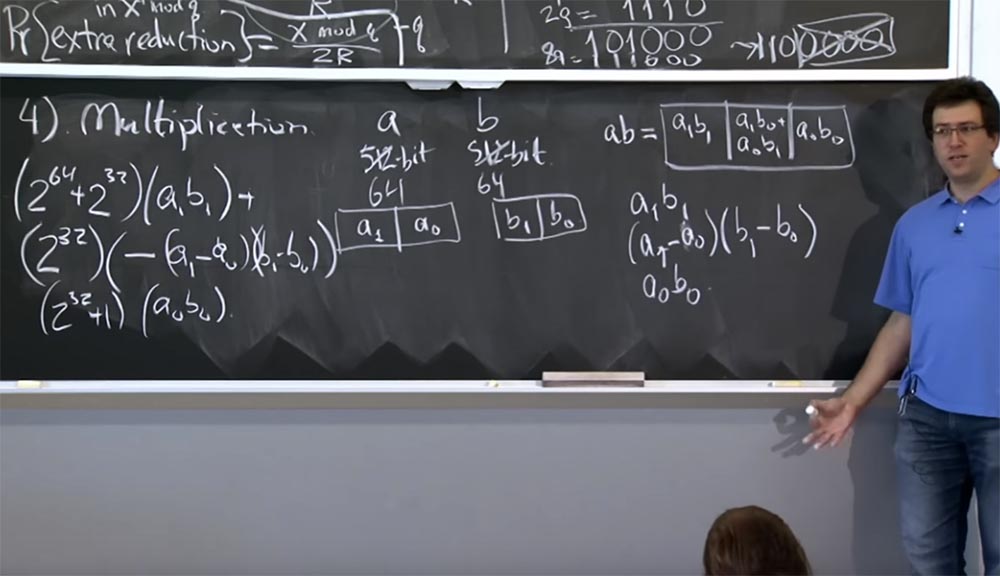
Alors, où est l'attaque temporelle? Comment ces gars utilisent-ils la multiplication de Karatsuba? Il s'avère qu'OpenSSL s'inquiète de deux types de multiplication que vous pourriez avoir à faire.
Le premier est la multiplication de deux grands nombres approximativement de la même taille. Cela se produit plusieurs fois lorsque nous effectuons une exponentiation modulaire, car toutes les valeurs que nous multiplierons auront une taille d'environ 512 bits. Par conséquent, lorsque nous multiplions c par y ou carré, nous multiplions deux choses d'environ la même taille. Dans ce cas, la méthode Karatsuba a beaucoup de sens, car elle réduit la taille des nombres au carré d'environ 1,58 fois, ce qui accélère considérablement le processus de calcul.
Le deuxième type de multiplication est lorsque OpenSSL multiplie deux nombres dont la taille diffère considérablement l'un de l'autre: l'un est très grand et l'autre est très petit. Dans ce cas, vous pouvez également utiliser la méthode Karatsuba, mais cela fonctionnera plus lentement que la multiplication primitive. Supposons que vous multipliez un nombre de 512 bits par un nombre de 64 bits, vous devrez augmenter chaque bit du premier nombre à une puissance de 64, entraînant un ralentissement du processus de 2n au lieu d'une accélération de n / 1,58. Par conséquent, ces gars qui utilisent OpenSSL ont essayé de faire plus intelligemment, et c'est là que les problèmes ont commencé.

Ils ont décidé qu'ils basculeraient dynamiquement entre la méthode efficace de Karatsuba et la méthode de multiplication des écoles élémentaires. Leur heuristique était la suivante. Si les deux nombres que vous multipliez sont constitués du même nombre de mots machine, ou ont au moins le même nombre de bits que les unités 32 bits, alors la méthode Karatsuba est utilisée. Si deux nombres diffèrent considérablement en taille l'un de l'autre, au carré ou directement simple, une multiplication normale est effectuée.

Dans ce cas, vous pouvez suivre la façon dont le passage à une autre méthode de multiplication se produit. Étant donné que le moment de la commutation ne passe pas sans laisser de trace, il sera visible après cela qu'il faut maintenant beaucoup plus de temps pour la multiplication ou beaucoup moins qu'auparavant. Les chercheurs ont profité de cette circonstance pour organiser une attaque en utilisant la méthode du chronométrage.

Je pense que j'ai fini de vous parler de toutes les astuces étranges que les gens utilisent lors de la mise en œuvre de RSA dans la pratique. Essayons maintenant de les assembler et de les utiliser par rapport à l'ensemble du serveur Web pour savoir comment vous pouvez "pincer" les bits qui nous intéressent dans le paquet réseau d'entrée.

Si vous vous souvenez de la conférence sur HTTPS, le serveur Web a une clé secrète. Il utilise cette clé secrète pour prouver qu'il est le propriétaire correct de tous les certificats via HTTPS ou TLS. Cela est dû au fait que les clients envoient des bits sélectionnés au hasard, ces bits sont chiffrés à l'aide de la clé publique du serveur et le serveur déchiffre ce message à l'aide du protocole TLS. Et si le message est vérifié, ces bits aléatoires sont utilisés pour établir une session de communication.

Mais dans notre cas, ce message ne sera pas vérifié, car il sera créé de manière spéciale, et lorsqu'il s'avérera que les bits supplémentaires ne correspondent pas, le serveur renverra une erreur dès qu'il aura fini de décrypter notre message.

Voici ce que nous allons faire ici. Le serveur - vous pouvez supposer qu'il s'agit d'Apache avec SSL ouvert - recevra un message du client qu'il considère comme du texte crypté avec ou du texte crypté hypothétique que le client a créé. La première chose que nous faisons avec le texte chiffré c est de le déchiffrer en utilisant la formule avec → (c ^d mod n) = m.

Si vous vous souvenez de la première optimisation, nous allons appliquer le théorème du reste chinois et diviser notre texte en deux parties: l'une pour calculer par mod p, l'autre par mod q, puis combiner les résultats. Tout d'abord, prenez c et représentez-le en deux quantités: la première est appelée c ₀ , elle sera égale à mod q, et la seconde est c ₁ , et elle sera égale à c mod p. Ensuite, nous ferons de même pour calculer c pour d mod p et c pour d mod q.



Ensuite, nous allons passer à la vue Montgomery car cela rendra nos multiplications très rapides. Donc, la prochaine chose que SSL va faire avec votre numéro est de calculer c ₀ ', qui sera égal à c ₀ R mod q et faire la même chose ci-dessous pour c1, je ne l'écrirai pas car il a la même apparence .

Maintenant que nous sommes passés à la forme Montgomery, nous pouvons enfin effectuer nos multiplications, et ici nous allons utiliser la technique de la «fenêtre coulissante». Dès que nous obtenons c ₀ ', nous faisons cette simple élévation de c ₀ ' à la puissance de d dans le mod q. Et ici, puisque nous calculons cette valeur pour d, nous utiliserons des «fenêtres coulissantes» pour des bits d'exposant d, et nous utiliserons également la méthode de Karatsuba ou la multiplication habituelle, selon la taille de nos opérandes.



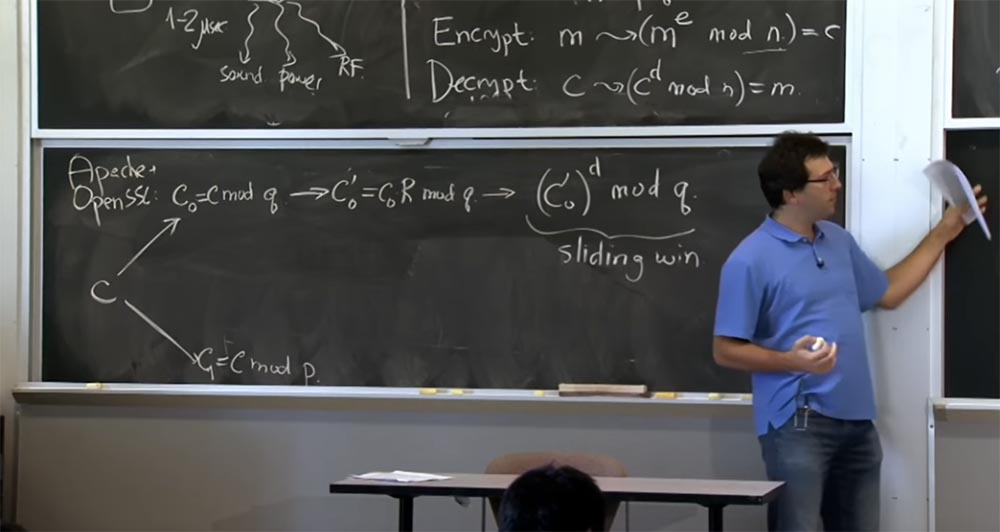
Donc, s'il s'avère que cette valeur c ₀ 'et le résultat de la quadrature précédemment obtenu sont de la même taille, nous utilisons la méthode de Karatsuba. Si c ₀ 'est très petit et que le résultat précédent de la multiplication est grand, alors nous allons quadriller et multiplier de la manière habituelle. Ici, nous utilisons des «fenêtres coulissantes» et la méthode Karatsuba au lieu d'une multiplication normale.



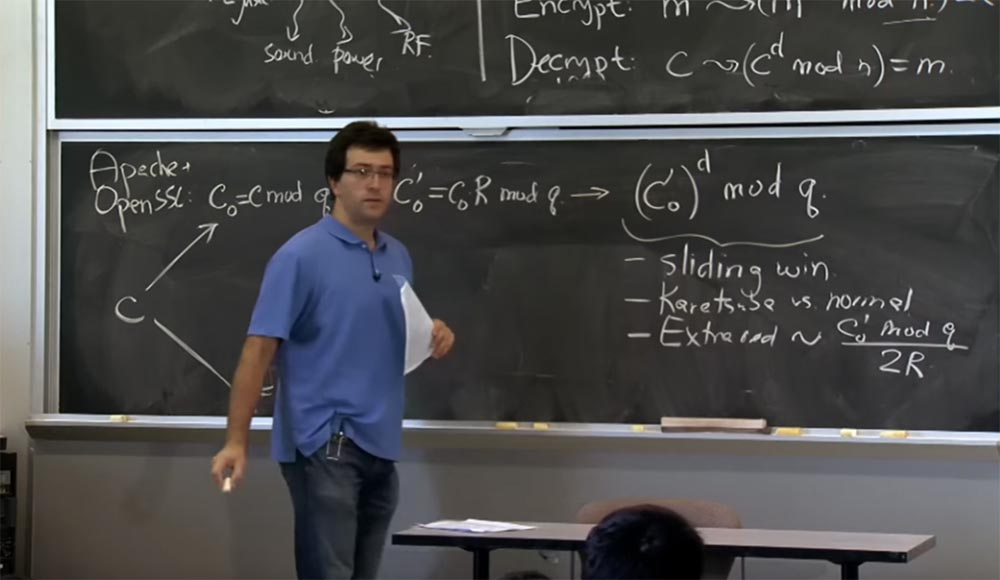
Toujours à ce stade, des réductions supplémentaires apparaissent. Parce qu'à chaque multiplication, les réductions supplémentaires seront proportionnelles à ce que nous élevons à la puissance du mod q, c'est-à-dire la valeur de (c ₀ ') ^d . Ici, avec une simple connexion de la formule, la probabilité de réductions supplémentaires sera proportionnelle à la valeur c ₀ 'mod q divisée par 2R. C'est à cet endroit qu'un peu apparaît qui affecte le timing.

En fait, il y a deux effets possibles: utiliser la méthode Karatsuba au lieu de la multiplication normale et l'apparition d'abréviations supplémentaires que vous allez faire.

Dans une seconde, vous verrez comment il peut être utilisé. Maintenant, lorsque vous obtenez ce résultat pour le mod q et que vous allez obtenir un résultat similaire pour le mod p, vous pouvez enfin recombiner ces deux parties en haut et en bas et utiliser CRT, le théorème du reste chinois.

Et ce que vous obtenez de CRT en conséquence ... désolé, je pense que nous devons d'abord le convertir à partir du formulaire Montgomery. Par conséquent, avant la recombinaison, nous convertissons la partie supérieure en l'expression (c ₀ ') ^d / R mod q et retournons notre valeur cd mod q. En partie basse, on obtient donc cd mod p.

Vous pouvez maintenant utiliser CRT pour obtenir la valeur de c ^d mod n. Désolé pour la petite police, je n'avais pas assez de tableau noir. À propos de la même chose que nous obtenons ici ci-dessous avec ₁ , et nous pouvons enfin obtenir notre résultat, c'est-à-dire le message m.



Ainsi, le serveur prend un paquet entrant qu'il reçoit, l'exécute à travers tout ce pipeline, exécute deux parties de ce pipeline et se termine par un message déchiffré m égal à cd mod m. Ensuite, il va vérifier le rembourrage de ce post. Dans le cas de notre attaque spécifique, nous avons créé de telle manière qu'en fait cet ajout ne correspondra pas. Nous avons choisi la valeur c pour les heuristiques qui ne chiffrent pas le message réel avec l'ajout de remplissage correct.

Ainsi, le module complémentaire ne réussit pas le test, le serveur devra enregistrer une erreur, envoyer un message d'erreur au client et se déconnecter. Nous allons donc mesurer le temps qu'il faudra au serveur pour transmettre notre message via ce pipeline. Vous avez des questions sur le processus de traitement d'un message par le serveur et la combinaison de toutes ces optimisations?

Public: à mon avis, il y a une erreur avec un indice de grandeur c.

Professeur: oui, vous avez raison, j'ajoute l'index 0, ici devrait être c ₀ ^d mod q.



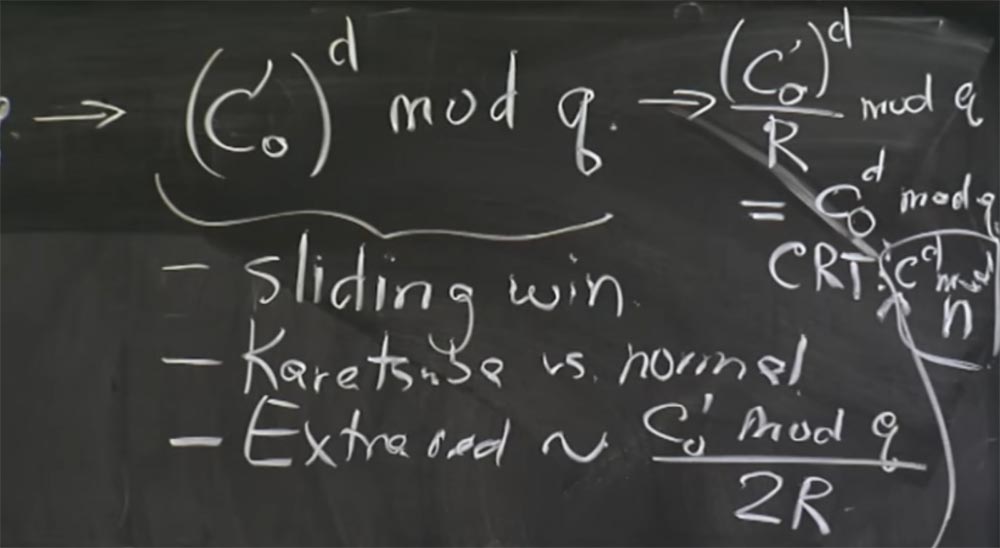Public: lorsque vous divisez par R mod q, n'y a-t-il aucune hypothèse sur la quantité q que vous devez ajouter pour réduire davantage les bits faibles en zéros?

Professeur: oui, vous avez raison, à ce stade final (c ₀ ') ^d / R mod q il peut y avoir des réductions supplémentaires. Nous devons donc faire cette division par R de la bonne manière, et probablement faire la même chose que de faire la réduction de Montgomery ici, lorsque nous divisons par R, pour reconvertir la valeur. Puisqu'au début des calculs, on ne sait pas exactement combien de q nous devons ajouter, nous utilisons la méthode de sélection, détruisons les zéros faibles, puis faisons de nouveau le mod q et, éventuellement, une réduction supplémentaire. Vous avez absolument raison, dans ce cas c'est exactement la même division par R mod q que pour chaque étape de multiplication de Montgomery.

Alors, comment profitez-vous de cela? Comment un attaquant peut-il résoudre la clé secrète d'un serveur en mesurant le temps nécessaire pour terminer les opérations? Ces gars-là ont un plan basé sur la supposition d'un bit de clé privée à la fois. Nous pouvons supposer que la clé secrète est l'exposant chiffré d, car vous connaissez e et connaissez n, il s'agit de la clé publique. La seule chose que vous ne savez pas est d.



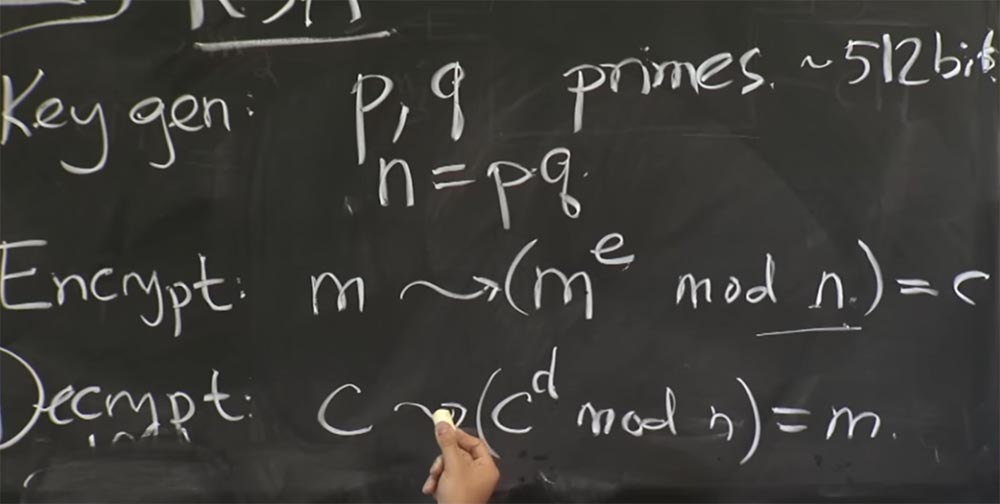
En fait, dans cette attaque, ils ne devinent pas directement la valeur de d, car c'est assez compliqué. Au lieu de cela, ils considèrent q ou p, peu importe laquelle de ces deux quantités. Une fois que vous avez deviné ce qui compte p ou q, vous pouvez calculer n = pq. Ensuite, si vous connaissez les valeurs de p et q, vous pouvez calculer la fonction φ dont nous avons parlé précédemment. Cela vous permet d'obtenir la valeur de d à partir de la valeur de e. Ainsi, cette factorisation de la valeur de n est extrêmement importante, elle doit être gardée secrète afin d'assurer la sécurité RSA.

Donc en fait, ces gars-là avaient l'intention de deviner la valeur q en analysant les timings de ce pipeline. Que font-ils pour ça? Ils sélectionnent soigneusement la valeur initiale de la valeur de c et mesurent le temps de son passage à travers le pipeline du serveur.

En particulier, cette attaque comporte deux parties, et vous devez prendre certaines mesures initiales pour deviner les premiers bits. Ensuite, dès que vous avez les premiers bits, vous pouvez deviner le bit suivant. Par conséquent, permettez-moi de ne pas vous dire en détail comment ils devinent les deux premiers bits, car en fait, il est beaucoup plus intéressant de considérer comment ils devinent le bit suivant. Si nous avons le temps, nous reviendrons sur la façon dont la devinette de plusieurs bits initiaux est décrite dans un article de conférence.

Supposons donc que vous ayez l'hypothèse g sur les bits de la valeur de ce q. Soit cette valeur composée de ces bits: g = g ₀ g ₁ g ₂ ... et ainsi de suite. Au contraire, ce n'est même pas g, mais les vrais bits de q, alors permettez-moi de le réécrire comme ceci: g = q ₀ q ₁ q ₂ .... Nous pensons que ces q sont des bits hauts, et nous essayons de deviner les bits de plus en plus bas. Supposons que nous connaissions la valeur de q jusqu'au bit qj, puis tous les zéros suivent. Vous n'avez aucune idée de ce que sont les autres bits.



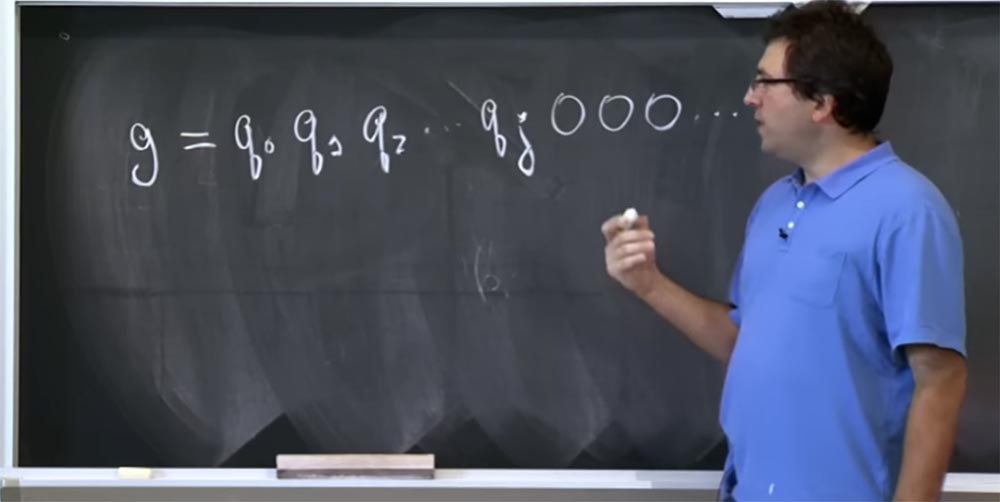
Ces gars-là ont essayé d'injecter cette conjecture g à cet endroit de notre pipeline: (c0 ') d mod q. Parce que c'est l'endroit où deux types d'optimisation sont utilisés: la méthode Karatsub au lieu de la multiplication habituelle et un nombre différent d'abréviations supplémentaires en fonction de la valeur de c ₀ '. En fait, ils ont essayé d'introduire deux suppositions différentes à cet endroit du pipeline: le premier, qui ressemble à g = q ₀ q ₁ q ₂ ... qj 000 ... 0000, et le second, qu'ils ont appelé g _high , qui se compose des mêmes bits hauts, mais à la place de tous les zéros à la fin, il y a une unité désignant un bit élevé, suivie à nouveau par des zéros:

g = q ₀ q ₁ q ₂ ... qj 100 ... 0000.

Comment cela aide-t-il ces gars à comprendre ce qui se passe? Il y a deux façons de procéder. Supposons que notre supposition g soit égale à la valeur c ₀ '. On peut supposer que ces g et g _high correspondent à la valeur c ₀ 'donnée sur le tableau de gauche. En fait, il est assez simple de le faire, car c ₀ 'est assez facile à calculer à l'envers à partir de la valeur d'entrée chiffrée c ₀ , il suffit de le multiplier par R.



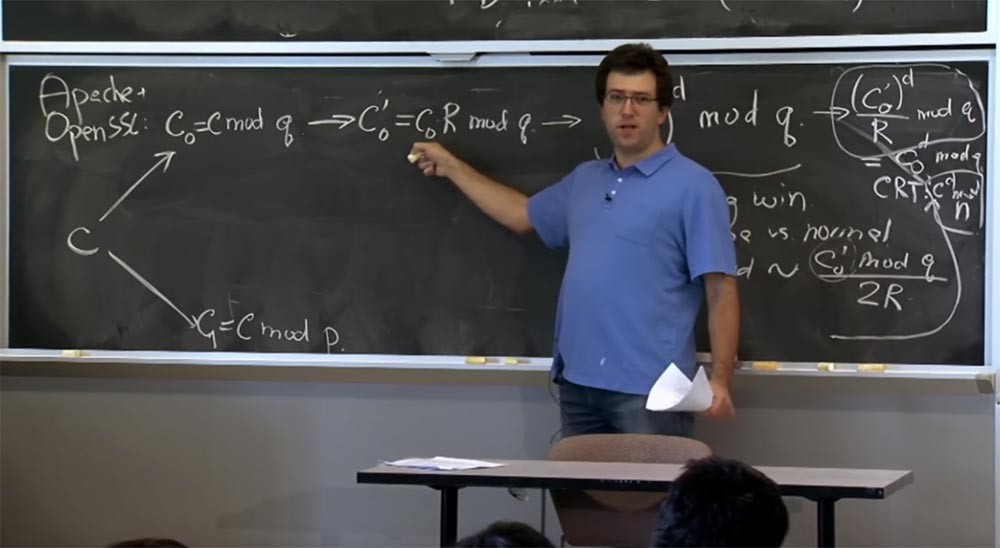
Par conséquent, pour deviner la valeur (c ₀ ') ^d , il leur suffit de prendre leur supposition, leur supposition g, et de la diviser d'abord par R, c'est-à-dire de diviser par 512 quelque chose de mod. Ensuite, ils vont le réintroduire, le serveur le multipliera par R et poursuivra le processus décrit dans notre schéma de pipeline.

Supposons donc que nous ayons pu mettre notre valeur entière sélectionnée au bon endroit. Alors, quel sera le temps de calcul c ₀ 'à d mod q?



Il y a deux options possibles où q s'inscrit dans cette image. Il se peut que q soit entre ces deux valeurs de g et g _high , car le bit suivant de q est 0. Ainsi, cette valeur - le premier 0 après qj - sera inférieure à q, mais cette valeur - 1 après q - sera supérieure à q. Cela se produit si le bit suivant de q est 0, ou il est possible que q soit au-dessus de ces deux valeurs si le bit suivant de q est 1.



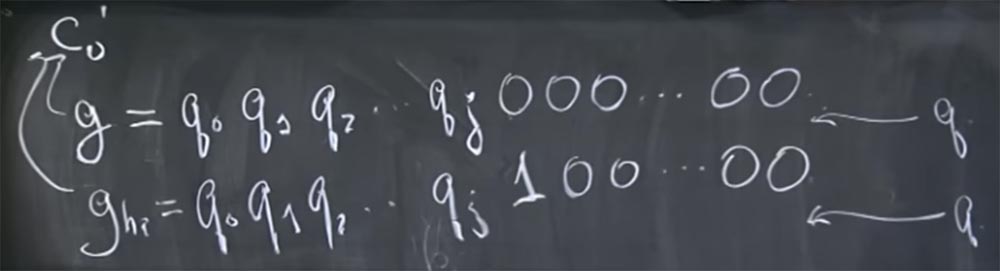
Nous pouvons maintenant dire quel sera le temps de déchiffrement de ces deux valeurs si q se situe entre elles, ou si q est situé au-dessus des deux.

Regardons la situation où q est situé au-dessus. Dans ce cas, tout est à peu près le même. Puisque ces deux valeurs sont inférieures à q, la valeur de ces choses dans le mod q sera approximativement la même. Ils sont légèrement différents en raison de ce bit supplémentaire, mais toujours plus ou moins la même taille. Et le nombre de réductions supplémentaires, réduction supplémentaire, ne différera probablement pas beaucoup non plus, car il est proportionnel à la valeur de c0 'mod q. Et pour g et g _des valeurs _élevées inférieures à q, elles sont toutes à peu près les mêmes. Aucun d'eux ne dépassera q et n'entraînera pas un grand nombre de réductions supplémentaires, car pour q supérieur à ces deux suppositions, le nombre de calculs par la méthode de Karatsuba par rapport au nombre de calculs ordinaires restera le même. En termes de cette relation, le serveur gérera g et g _high également. Par conséquent, le serveur est sur le point de créer à peu près la même quantité d'abréviations supplémentaires pour ces deux valeurs. Ainsi, si vous voyez que le serveur passe le même temps à répondre à ces conjectures, alors vous devriez probablement supposer qu'il y a vraiment 1 dans la valeur _élevée g à ce stade.



D'un autre côté, si q est situé entre ces deux valeurs, alors il y a deux choses possibles qui peuvent provoquer des changements de commutation et de synchronisation. L'une des choses est que, puisque g _{élevé est} légèrement supérieur à q, le nombre de coupes supplémentaires sera proportionnel à c ₀ 'mod q, qui est très petit, car c ₀ ' est q plus quelques bits dans cette séquence de bits supplémentaires de 100 ... 00. Ainsi, le nombre de réductions supplémentaires sera plus visible et tout commencera à se produire plus rapidement.
, , , , , : «, !». , g c ₀ ' , q, , g _high q, g _high mod q . , . – , , .

c ₀ ' mod q. c ₀ g _high , q, , g q. , . , , . , 32- , .

, 32- , , , . , . 32 , , - . , , 32, , , , .

, , , . , q 1, , q 0, , g _high q , , .

. , . , . , , 1-2 . , , Ethernet.
, . . , 7 . , , -, , ?

: ?

: , , , , , . , .

, , 7 , , 7 . 7 g, 7 g + 1, g + 2 7 g + 400. g, g, , 7 400, ?



: , , ?

: , , , — (c ₀ ') ^d . . , , , mod p. , , . , g, 1, 2, 3, , .

, , – 100…00. , mod p, , mod p . « », , (c ₀ ') ^d , . ?

: , ?

: - , q. , q, , , .

: c ₀ '?

: c ₀ ', c, c ₀ ' R mod n.



, «» , c ₀ = mod q, c ₀ = ((c ₀ ' R ^-1 ) mod n) mod q. R, R. c ₀ ', (c ₀ ') ^d mod q. , , , , R. , R = 2 ⁵¹² . , .

: mod p ?

: , , ? , ! , .


.

Merci de rester avec nous. Aimez-vous nos articles? Vous voulez voir des matériaux plus intéressants? Soutenez-nous en passant une commande ou en le recommandant à vos amis, une réduction de 30% pour les utilisateurs Habr sur un analogue unique de serveurs d'entrée de gamme que nous avons inventés pour vous: Toute la vérité sur VPS (KVM) E5-2650 v4 (6 cœurs) 10 Go DDR4 240 Go SSD 1 Gbps à partir de 20 $ ou comment diviser le serveur? (les options sont disponibles avec RAID1 et RAID10, jusqu'à 24 cœurs et jusqu'à 40 Go de DDR4).

VPS (KVM) E5-2650 v4 (6 Cores) 10GB DDR4 240GB SSD 1Gbps , .

Dell R730xd 2 fois moins cher? Nous avons seulement 2 x Intel Dodeca-Core Xeon E5-2650v4 128 Go DDR4 6x480 Go SSD 1 Gbps 100 TV à partir de 249 $ aux Pays-Bas et aux États-Unis! Pour en savoir plus sur la création d'un bâtiment d'infrastructure. classe utilisant des serveurs Dell R730xd E5-2650 v4 coûtant 9 000 euros pour un sou?