👩🏽‍🏫 🈴 👨🏻‍⚕️ Julia et le mouvement d'une particule chargée dans un champ électromagnétique 🙋🏾 👨🏾‍🌾 👬

Nous renforçons les compétences de résolution et de visualisation d'équations différentielles en utilisant l'une des équations évolutives les plus courantes à titre d'exemple, rappelez-vous le bon vieux Scilab et essayez de comprendre si nous en avons besoin ... Sous la coupe (kilo-octets pour sept cents)

Assurez-vous que le logiciel est récent

julia>] (v1.0) pkg>update #   (v1.0) pkg> status Status `C:\Users\\.julia\environments\v1.0\Project.toml` [537997a7] AbstractPlotting v0.9.0 [ad839575] Blink v0.8.1 [159f3aea] Cairo v0.5.6 [5ae59095] Colors v0.9.5 [8f4d0f93] Conda v1.1.1 [0c46a032] DifferentialEquations v5.3.1 [a1bb12fb] Electron v0.3.0 [5789e2e9] FileIO v1.0.2 [5752ebe1] GMT v0.5.0 [28b8d3ca] GR v0.35.0 [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git) [4c0ca9eb] Gtk v0.16.4 [a1b4810d] Hexagons v0.2.0 [7073ff75] IJulia v1.14.1+ [`C:\Users\\.julia\dev\IJulia`] [6218d12a] ImageMagick v0.7.1 [c601a237] Interact v0.9.0 [b964fa9f] LaTeXStrings v1.0.3 [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git) [7269a6da] MeshIO v0.3.1 [47be7bcc] ORCA v0.2.0 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git) [91a5bcdd] Plots v0.21.0 [438e738f] PyCall v1.18.5 [d330b81b] PyPlot v2.6.3 [c4c386cf] Rsvg v0.2.2 [60ddc479] StatPlots v0.8.1 [b8865327] UnicodePlots v0.3.1 [0f1e0344] WebIO v0.4.2 [c2297ded] ZMQ v1.0.0

Passons en revue les anciens guides

et passez à l'énoncé du problème

Le mouvement des particules chargées dans un champ électromagnétique

Sur une particule chargée avec une charge $q$ se déplacer dans EMF avec vitesse $u$ la force de Lorentz agit: $\ vec {F} _L = q \ left (\ vec {E} + \ left [\ vec {u} \ times \ vec {B} \ right] \ right)$ . Cette formule est valable avec un certain nombre de simplifications. En négligeant les corrections à la théorie de la relativité, nous considérons que la masse des particules est constante, donc l'équation du mouvement a la forme: $\ frac {d} {dt} (m \ vec {u}) = q \ left (\ vec {E} + \ left [\ vec {u} \ times \ vec {B} \ right] \ right)$

Dirigeons l'axe Y le long du champ électrique, l'axe Z le long du champ magnétique et supposons pour simplifier que la vitesse initiale des particules se situe dans le plan XY. Dans ce cas, toute la trajectoire de la particule se situera également dans ce plan. Les équations du mouvement prendront la forme:

\ left \ {\ begin {matrix} m \ ddot {x} = qB \ dot {y} \\ m \ ddot {y} = qE-qB \ dot {x} \ end {matrix} \ right.

$\ left \ {\ begin {matrix} m \ ddot {x} = qB \ dot {y} \\ m \ ddot {y} = qE-qB \ dot {x} \ end {matrix} \ right.$

Incommensurable: $x ^ * = \ frac {x} {\ lambda}, \, y ^ * = \ frac {y} {\ lambda}, \, \ tau = \ frac {ct} {\ lambda}, \, B ^ * = \ frac {Bmc} {q \ lambda}, \, E ^ * = \ frac {Emc ^ 2} {q \ lambda}$ . Les astérisques indiquent les quantités dimensionnelles, et $\ lambda$ - la taille caractéristique du système physique considéré. Nous obtenons un système sans dimension d'équations de mouvement d'une particule chargée dans un champ magnétique:

\ left \ {\ begin {matrix} \ frac {d ^ 2x} {d \ tau ^ 2} = B \ frac {dy} {d \ tau} \\ \ frac {d ^ 2y} {d \ tau ^ 2} = EB \ frac {dx} {d \ tau} \ end {matrix} \ droite.

$\ left \ {\ begin {matrix} \ frac {d ^ 2x} {d \ tau ^ 2} = B \ frac {dy} {d \ tau} \\ \ frac {d ^ 2y} {d \ tau ^ 2} = EB \ frac {dx} {d \ tau} \ end {matrix} \ droite.$

Abaissons l'ordre:

\ left \ {\ begin {matrix} \ frac {dx} {d \ tau} = U_x \\ \ frac {dy} {d \ tau} = U_y \\ \ frac {dU_x} {d \ tau} = BU_y \\ \ frac {dU_y} {d \ tau} = E-BU_x \ end {matrix} \ droite.

$\ left \ {\ begin {matrix} \ frac {dx} {d \ tau} = U_x \\ \ frac {dy} {d \ tau} = U_y \\ \ frac {dU_x} {d \ tau} = BU_y \\ \ frac {dU_y} {d \ tau} = E-BU_x \ end {matrix} \ droite.$

Comme configuration initiale du modèle, nous choisissons: $B = 2$ T $E = 5 \ cdot 10 ^ 4$ V / m $v_0 = 7 \ cdot 10 ^ 4$ m / s Pour une solution numérique, nous utilisons le package DifferentialEquations :

Code et graphiques

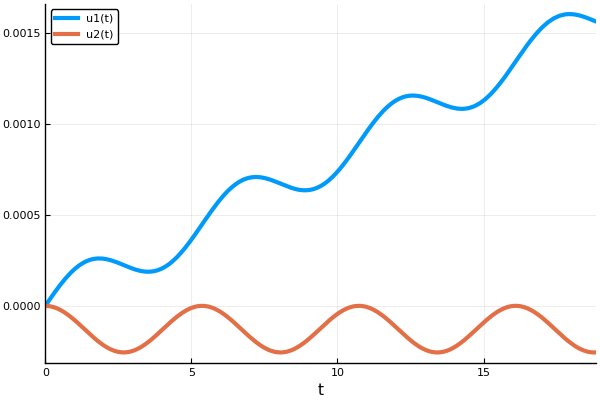
 using DifferentialEquations, Plots pyplot() M = 9.11e-31 # kg q = 1.6e-19 # C C = 3e8 # m/s λ = 1e-3 # m function modelsolver(Bo = 2., Eo = 5e4, vel = 7e4) B = Bo*q*λ / (M*C) E = Eo*q*λ / (M*C*C) vel /= C A = [0. 0. 1. 0.; 0. 0. 0. 1.; 0. 0. 0. B; 0. 0. -B 0.] syst(u,p,t) = A * u + [0.; 0.; 0.; E] # ODE system u0 = [0.0; 0.0; vel; 0.0] # start cond-ns tspan = (0.0, 6pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, Euler(), dt = 1e-4, save_idxs = [1, 2], timeseries_steps = 1000) end Solut = modelsolver() plot(Solut)

Ici, nous utilisons la méthode Euler, pour laquelle le nombre d'étapes est spécifié. De plus, la solution entière du système n'est pas enregistrée dans la matrice de réponse, mais seulement 1 et 2 indices, c'est-à-dire les coordonnées du X et du joueur (nous n'avons pas besoin de vitesses).

 X = [Solut.u[i][1] for i in eachindex(Solut.u)] Y = [Solut.u[i][2] for i in eachindex(Solut.u)] plot(X, Y, xaxis=("X"), background_color=RGB(0.1, 0.1, 0.1)) title!(" ") yaxis!("Y") savefig("XY1.png")#

Vérifiez le résultat. Nous introduisons une nouvelle variable au lieu de x $\ tilde {x} = x-ut$ . Ainsi, une transition est effectuée vers un nouveau système de coordonnées se déplaçant par rapport à l'original avec une vitesse u en direction de l'axe X :

\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = qB \ dot {y} / m \\ \ ddot {y} = qE / m-qB \ dot {x} / m -qBu / m \ end {matrice} \ droite.

$\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = qB \ dot {y} / m \\ \ ddot {y} = qE / m-qB \ dot {x} / m -qBu / m \ end {matrice} \ droite.$

Si vous choisissez $u = E / B$ et dénote $\ omega = qB / m$ , alors le système sera simplifié:

\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = \ omega \ dot {y} \\ \ ddot {y} = - \ omega \ dot {\ tilde {x}} \ end { matrice} \ droite.

$\ left \ {\ begin {matrix} \ ddot {\ tilde {x}} = \ omega \ dot {y} \\ \ ddot {y} = - \ omega \ dot {\ tilde {x}} \ end { matrice} \ droite.$

Le champ électrique a disparu des dernières égalités, et ce sont les équations de mouvement d'une particule sous l'influence d'un champ magnétique uniforme. Ainsi, la particule dans le nouveau système de coordonnées (x, y) doit se déplacer dans un cercle. Étant donné que ce nouveau système de coordonnées se déplace par rapport à l'original avec la vitesse $u = E / B$ , le mouvement des particules résultant consistera en un mouvement uniforme le long de l'axe X et une rotation autour du cercle dans le plan XY . Comme vous le savez, la trajectoire qui se produit lorsque ces deux mouvements sont additionnés est généralement un trochoïde . En particulier, si la vitesse initiale est nulle, le cas le plus simple de mouvement de ce type est réalisé - le long de la cycloïde .
Assurons-nous que la vitesse de dérive est vraiment égale à E / V. Pour ce faire:

nous gâcherons la matrice de réponse en définissant une valeur délibérément inférieure au lieu du premier élément (maximum)
nous trouvons le numéro de l'élément maximum dans la deuxième colonne de la matrice de réponse, qui est retardé en ordonnée
nous calculons la vitesse de dérive sans dimension en divisant la valeur maximale des abscisses par la valeur de temps correspondante

 Y[1] = -0.1 numax = argmax( Y ) X[numax] / Solut.t[numax]

Sortie: 8.334546850446588e-5

 B = 2*q*λ / (M*C) E = 5e4*q*λ / (M*C*C) E/B

Sortie: 8.33333333333333332e-5
Jusqu'au septième ordre!
Pour plus de commodité, nous définissons une fonction qui prend les paramètres du modèle et la signature du graphique, qui servira également de nom au fichier png créé dans le dossier du projet (fonctionne dans Juno / Atom et Jupyter). Contrairement à Gadfly , où les graphiques ont été créés en couches , puis affichés par la fonction plot () , dans Plots, afin de créer différents graphiques dans une seule image, le premier d'entre eux est créé par la fonction plot () et les suivants sont ajoutés à l'aide de plot! () . Les noms des fonctions qui modifient les objets acceptés dans Julia sont habituels pour se terminer par un point d'exclamation.

 function plotter(ttle = "qwerty", Bo = 2, Eo = 4e4, vel = 7e4) Ans = modelsolver(Bo, Eo, vel) X = [Ans.u[i][1] for i in eachindex(Ans.u)] Y = [Ans.u[i][2] for i in eachindex(Ans.u)] plot!(X, Y) p = title!(ttle) savefig( p, ttle * ".png" ) end

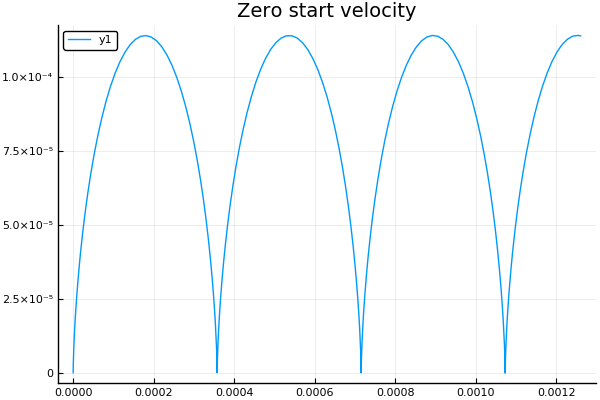
A vitesse initiale nulle, comme prévu, on obtient une cycloïde :

 plot() plotter("Zero start velocity", 2, 4e4, 7e4)

Nous obtenons la trajectoire de la particule lorsque l'induction, l'intensité et le changement de signe de charge. Permettez-moi de vous rappeler qu'un point signifie l'exécution séquentielle d'une fonction avec tous les éléments du tableau

Niché

 plot() plotter.("B   ", 0, [3e4 4e4 5e4 6e4] )

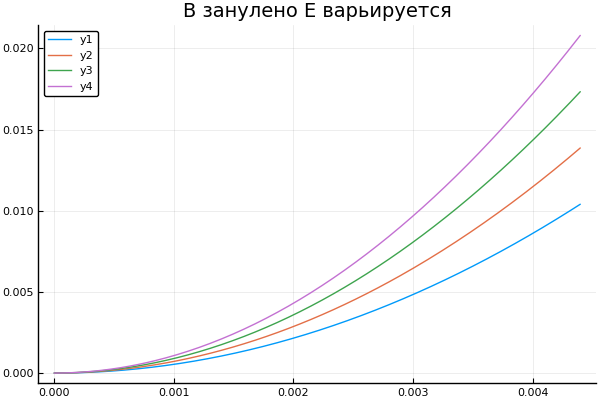
 plot() plotter.("E  B ", [1 2 3 4], 0 )

 q = -1.6e-19 # C plot() plotter.(" ")

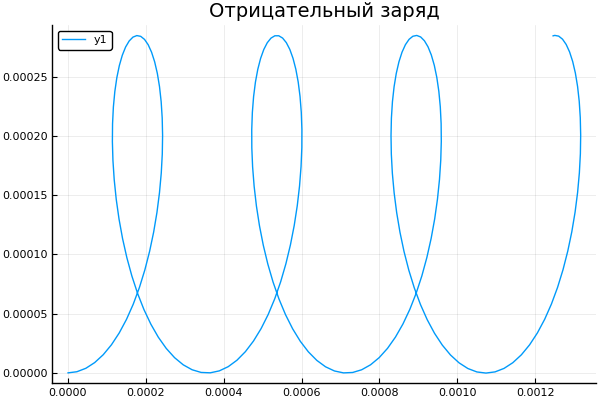
Et voyons comment le changement de la vitesse initiale affecte la trajectoire de la particule:

 plot() plotter.(" ", 2, 5e4, [2e4 4e4 6e4 8e4] )

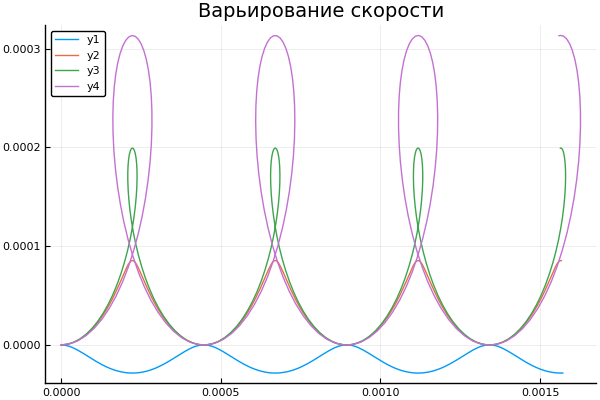
Un peu sur Scilab

Sur Habré, il y a déjà suffisamment d'informations sur Silab, par exemple 1 , 2 , et ici sur Octave, nous nous limiterons donc aux liens vers Wikipédia et vers la page d'accueil .

Pour ma part, j'ajouterai la présence d'une interface pratique avec des cases à cocher, des boutons et des graphiques, et un outil de modélisation visuelle Xcos assez intéressant. Ce dernier peut être utilisé, par exemple, pour simuler un signal en électrotechnique:

Spoiler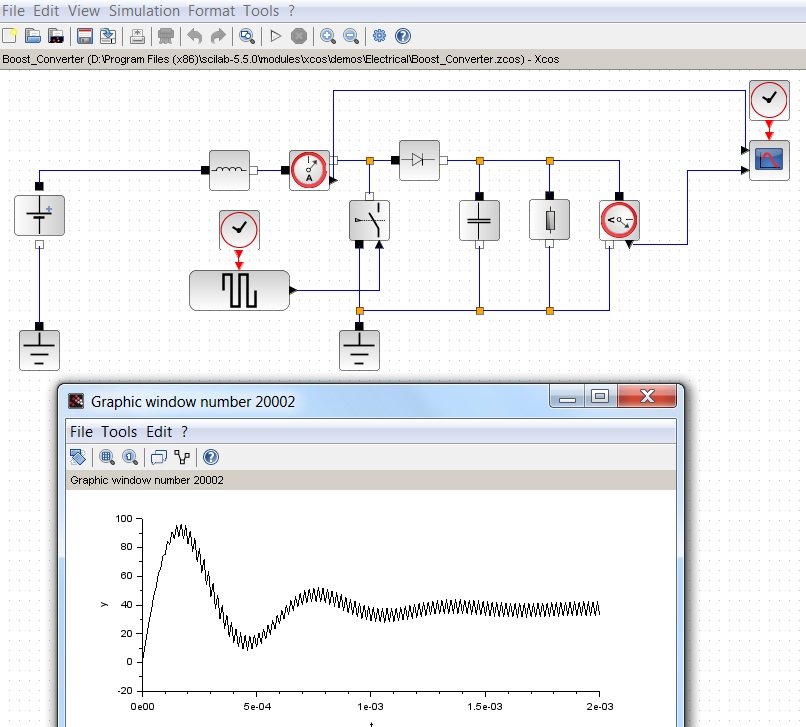

Et voici un guide très pratique:

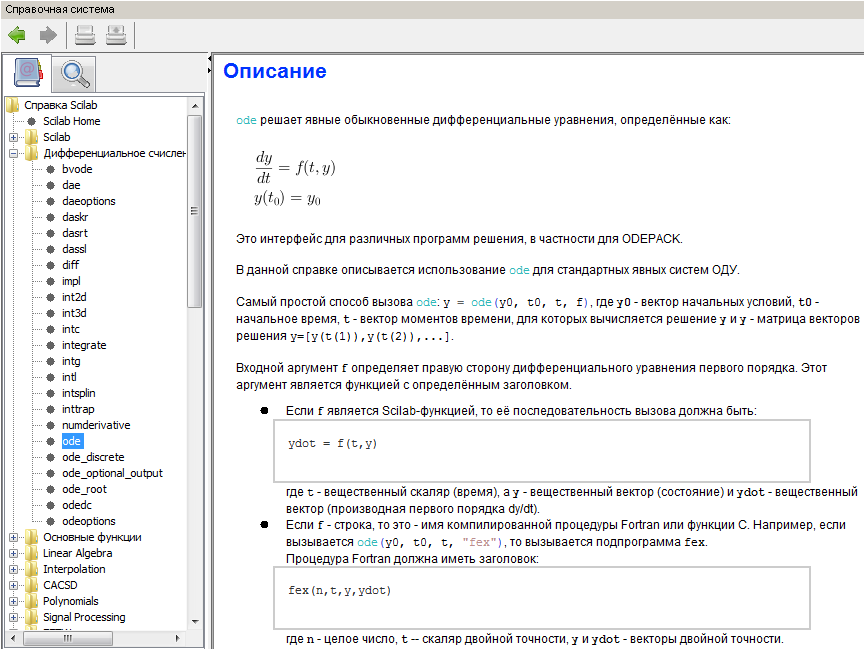
En fait, notre tâche peut également être résolue dans Scilab:

Code et photos

 clear function du = syst(t, u, A, E) du = A * u + [0; 0; 0; E] // ODE system endfunction function [tspan, U] = modelsolver(Bo, Eo, vel) B = Bo*q*lambda / (M*C) E = Eo*q*lambda / (M*C*C) vel = vel / C u0 = [0; 0; vel; 0] // start cond-ns t0 = 0.0 tspan = t0:0.1:6*%pi // time period A = [0 0 1 0; 0 0 0 1; 0 0 0 B; 0 0 -B 0] U = ode("rk", u0, t0, tspan, list(syst, A, E) ) endfunction M = 9.11e-31 // kg q = 1.6e-19 // C C = 3e8 // m/s lambda = 1e-3 // m [cron, Ans1] = modelsolver( 2, 5e4, 7e4 ) plot(cron, Ans1 ) xtitle ("   ","t","x, y, dx/dt, dy/dt"); legend ("x", "y", "Ux", "Uy"); scf(1)//    plot(Ans1(1, :), Ans1(2, :) ) xtitle (" ","x","y"); xs2png(0,'graf1');//       xs2jpg(1,'graf2');// ,  -

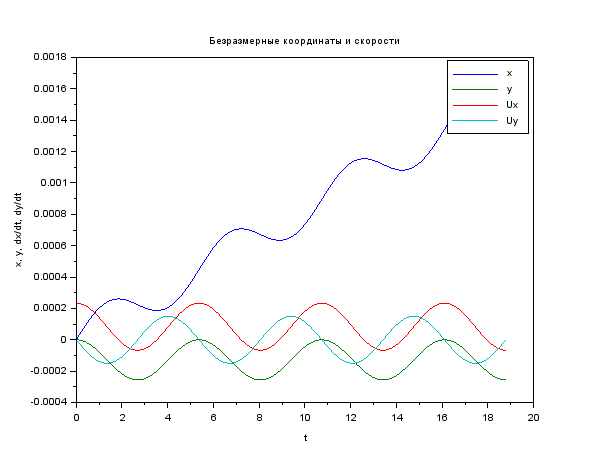
Voici des informations sur la fonction de résolution des différences d'ode. En principe, la question se pose

Pourquoi avons-nous besoin de Julia?

... s'il y a des choses merveilleuses comme Scilab, Octave et Numpy, Scipy?
À propos des deux derniers, je ne dirai pas - je ne l'ai pas essayé. Et en général, la question est compliquée, alors jetons un coup d'œil:

Scilab
Sur un disque dur, cela prendra un peu plus de 500 Mo, il démarre rapidement et immédiatement, il y a le calcul différentiel, les graphiques et tout le reste. Bon pour les débutants: un excellent guide (principalement localisé), il existe de nombreux livres en russe. Des erreurs internes ont déjà été dites ici et ici , et comme le produit est très niche, la communauté est lente, et les modules supplémentaires sont très rares.

Julia
Au fur et à mesure que des packages sont ajoutés (en particulier tout python-à la Jupyter et Mathplotlib), il passe de 376 Mo à un peu plus de six gigaoctets. Elle n'épargne pas non plus de RAM: au début de 132 Mo et après avoir tracé des plannings sur Jupiter, elle atteindra sereinement 1 Go. Si vous travaillez dans Juno , alors tout est presque comme dans Scilab : vous pouvez exécuter le code immédiatement dans l'interpréteur, vous pouvez imprimer dans le bloc-notes intégré et l'enregistrer sous forme de fichier, il existe un navigateur de variables, un journal des commandes et une aide en ligne. Personnellement, je suis indigné du manque de clear () , c'est-à-dire que j'ai exécuté le code, puis j'ai commencé à le corriger et à le renommer, et les anciennes variables sont restées (il n'y a pas de navigateur de variables dans Jupiter).

Mais tout cela n'est pas critique. Scilab est tout à fait approprié pour le premier couple, faire un front, un curseur ou calculer quelque chose entre les deux est un outil très improvisé. Bien qu'il existe également un support pour le calcul parallèle et l'appel de fonctions sishn / Fortran, pour lesquelles il ne peut pas être utilisé sérieusement. Les grands tableaux le terrifient, pour en définir des multidimensionnels, vous devez faire face à toutes sortes d'obscurantisme , et les calculs au-delà de la portée des tâches classiques peuvent tout laisser tomber avec le système d'exploitation.

Et après toutes ces douleurs et déceptions, vous pouvez également passer en toute sécurité à Julia pour ratisser ici aussi. Nous continuerons à étudier, le bénéfice de la communauté est très réactif, les problèmes se règlent rapidement et Julia a de nombreuses autres fonctionnalités intéressantes qui transformeront le processus d'apprentissage en un voyage passionnant!

Julia et le mouvement d'une particule chargée dans un champ électromagnétique

Le mouvement des particules chargées dans un champ électromagnétique

Un peu sur Scilab

Pourquoi avons-nous besoin de Julia?

More articles: