• Programme éducatif sur la théorie des probabilités (article introductif, facultatif)
  
• Introduction aux systèmes linéaires d'équations
  
• Méthodes par éléments finis
  
• Minimisation des formes quadratiques et exemples de problèmes OLS
  
• Des moindres carrés aux réseaux de neurones
  

Donc, un autre article du cycle des «maths sur les doigts ». Aujourd'hui, nous continuons la discussion sur les méthodes des moindres carrés, mais cette fois du point de vue du programmeur. Il s'agit d'un autre article de la série, mais il se distingue, car il ne nécessite généralement aucune connaissance des mathématiques. L'article a été conçu comme une introduction à la théorie, donc à partir des compétences de base, il nécessite la capacité d'allumer un ordinateur et d'écrire cinq lignes de code. Bien sûr, je ne m'attarderai pas sur cet article, et dans un proche avenir, je publierai une suite. Si je peux trouver assez de temps, alors j'écrirai un livre à partir de ce matériel. Le public cible est les programmeurs, donc Habr est le bon endroit pour intervenir. En général, je n'aime pas écrire des formules, et j'aime vraiment apprendre des exemples, il me semble que c'est très important - pas seulement regarder les gribouillis sur la commission scolaire, mais tout essayer sur la dent.

Commençons donc. Imaginons que j'ai une surface triangulée avec un scan de mon visage (dans l'image de gauche). Que dois-je faire pour améliorer les fonctionnalités, transformer cette surface en un masque grotesque?



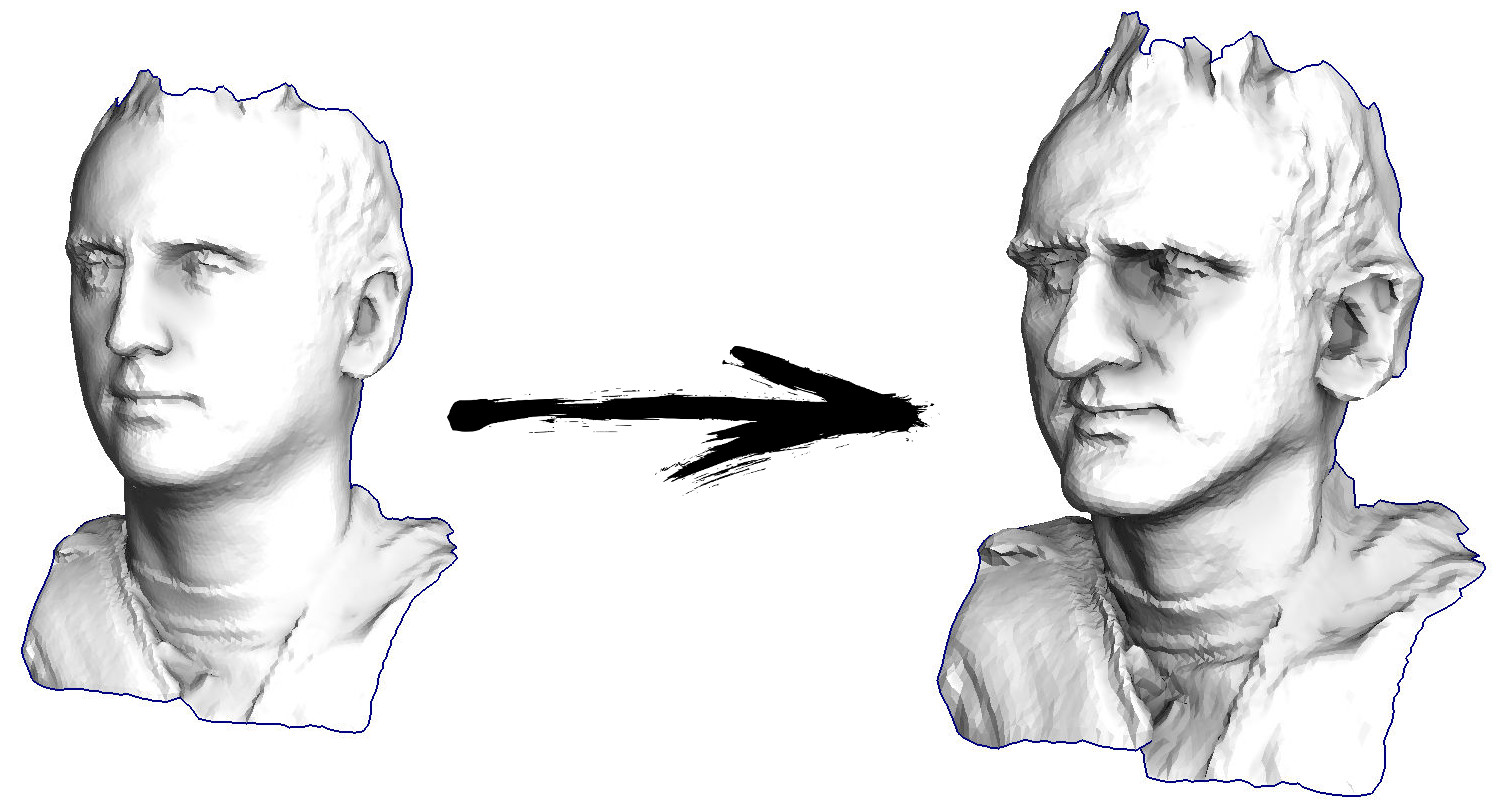
Dans ce cas particulier, je résous une équation différentielle elliptique nommée Simeon Demi Poisson . Chers programmeurs, jouons à un jeu: devinez combien de lignes il y a dans le code C ++ qui le décide? Les bibliothèques tierces ne peuvent pas être appelées, nous n'avons qu'un compilateur nu à notre disposition. La réponse est sous la coupe.

En fait, vingt lignes de code suffisent pour un solveur. Si vous comptez avec tout, tout, y compris l'analyseur du fichier de modèle 3D, restez dans les deux cents lignes - crachez.

Exemple 1: lissage des données

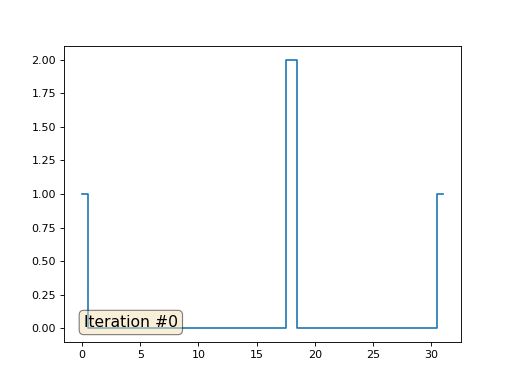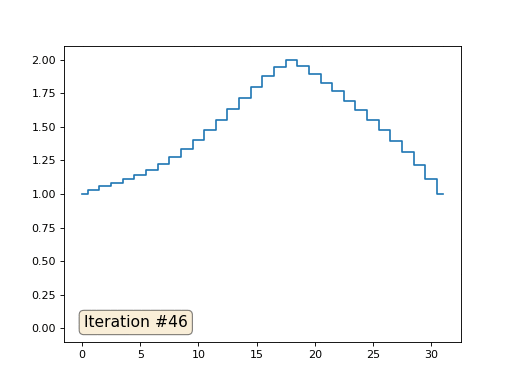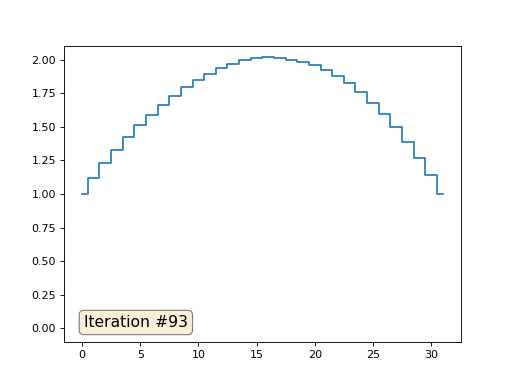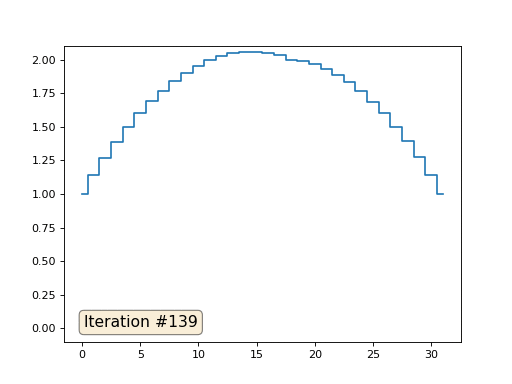
Parlons de son fonctionnement. Partons de loin, imaginons que nous ayons un tableau régulier f, par exemple, de 32 éléments, initialisé comme suit:



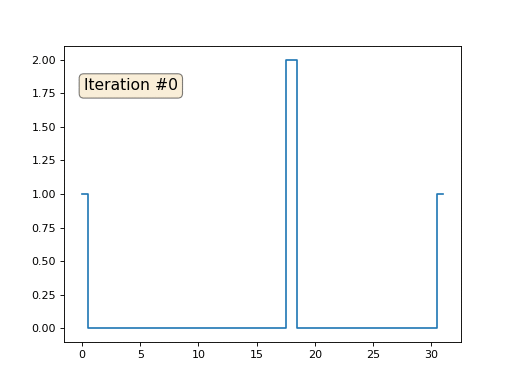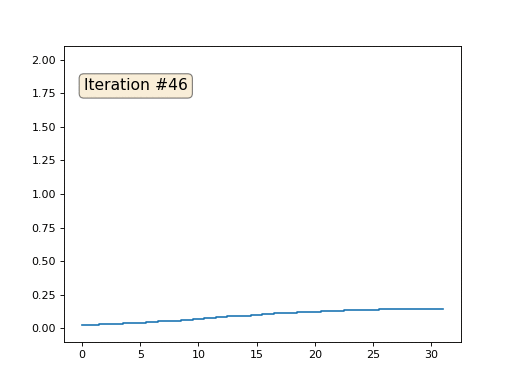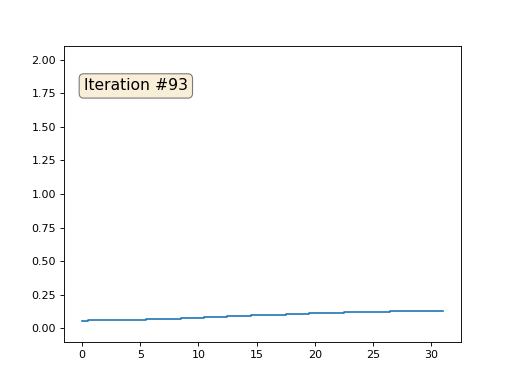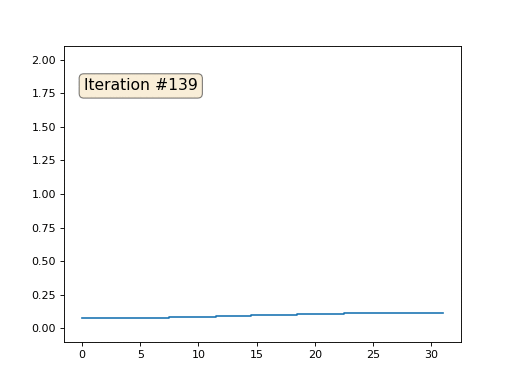
Et puis nous effectuerons mille fois la procédure suivante: pour chaque cellule f [i] nous y écrivons la valeur moyenne des cellules voisines: f [i] = (f [i-1] + f [i + 1]) / 2. Pour le rendre plus clair, voici le code complet:

import matplotlib.pyplot as plt f = [0.] * 32 f[0] = f[-1] = 1. f[18] = 2. plt.plot(f, drawstyle='steps-mid') for iter in range(1000): f[0] = f[1] for i in range(1, len(f)-1): f[i] = (f[i-1]+f[i+1])/2. f[-1] = f[-2] plt.plot(f, drawstyle='steps-mid') plt.show() 

Chaque itération lissera les données de notre tableau, et après mille itérations, nous obtiendrons une valeur constante dans toutes les cellules. Voici une animation des cent cinquante premières itérations:



Si vous ne comprenez pas pourquoi l'anti-aliasing se produit, arrêtez-vous maintenant, prenez un stylo et essayez de dessiner des exemples, sinon cela n'a aucun sens de continuer à lire. La surface triangulée est essentiellement la même que celle de cet exemple. Imaginez que pour chaque sommet, nous trouvons ses voisins, calculons leur centre de masse et déplacions notre sommet vers ce centre de masse, et ainsi dix fois. Le résultat sera comme ceci:



Bien sûr, si vous ne vous arrêtez pas à dix itérations, après un certain temps, toute la surface sera compressée en un point exactement de la même manière que dans l'exemple précédent, tout le tableau est rempli avec la même valeur.

Exemple 2: amélioration / atténuation des fonctionnalités

Le code complet est disponible sur le github , mais ici je vais donner la partie la plus importante, en omettant uniquement la lecture et l'écriture des modèles 3D. Ainsi, le modèle triangulé pour moi est représenté par deux tableaux: verts et faces. Le tableau des verts n'est qu'un ensemble de points tridimensionnels, ce sont les sommets du maillage polygonal. Le tableau de faces est un ensemble de triangles (le nombre de triangles est égal à faces.size ()), pour chaque triangle les indices du tableau de sommets sont stockés dans le tableau. Le format des données et le travail que j'ai décrit en détail dans mon cours de conférences sur l'infographie. Il y a aussi un troisième tableau, que je raconte à partir des deux premiers (plus précisément, uniquement à partir du tableau des visages) - vvadj. Il s'agit d'un tableau qui pour chaque sommet (le premier index d'un tableau à deux dimensions) stocke les indices de ses voisins (deuxième index).

 std::vector<Vec3f> verts; std::vector<std::vector<int> > faces; std::vector<std::vector<int> > vvadj; 

La première chose que je fais est que pour chaque sommet de ma surface, je considère le vecteur de courbure. Illustrons: pour le sommet actuel v, j'itère sur tous ses voisins n1-n4; puis je compte leur centre de masse b = (n1 + n2 + n3 + n4) / 4. Eh bien, le vecteur de courbure final peut être calculé comme c = vb, il ne ressemble en rien aux différences finies ordinaires pour la dérivée seconde .



Directement dans le code, cela ressemble à ceci:

  std::vector<Vec3f> curvature(verts.size(), Vec3f(0,0,0)); for (int i=0; i<(int)verts.size(); i++) { for (int j=0; j<(int)vvadj[i].size(); j++) { curvature[i] = curvature[i] - verts[vvadj[i][j]]; } curvature[i] = verts[i] + curvature[i] / (float)vvadj[i].size(); } 

Eh bien, nous faisons la chose suivante plusieurs fois (voir l'image précédente): nous déplaçons le sommet v à v: = b + const * c. Veuillez noter que si la constante est égale à un, alors notre sommet ne se déplacera nulle part! Si la constante est nulle, le sommet est remplacé par le centre de masse des sommets voisins, ce qui lissera notre surface. Si la constante est supérieure à l'unité (l'image du titre a été créée en utilisant const = 2.1), le sommet se déplacera dans la direction du vecteur de courbure de surface, renforçant les détails. Voici à quoi cela ressemble dans le code:

  for (int it=0; it<100; it++) { for (int i=0; i<(int)verts.size(); i++) { Vec3f bary(0,0,0); for (int j=0; j<(int)vvadj[i].size(); j++) { bary = bary + verts[vvadj[i][j]]; } bary = bary / (float)vvadj[i].size(); verts[i] = bary + curvature[i]*2.1; // play with the coeff here } } 

Soit dit en passant, si elle est inférieure à l'unité, les détails s'affaibliront au contraire (const = 0,5), mais cela ne sera pas équivalent au simple lissage, le "contraste de l'image" restera:



Veuillez noter que mon code génère un fichier de modèle 3D au format Wavefront .obj , que j'ai rendu dans un programme tiers. Vous pouvez voir le modèle résultant, par exemple, dans la visionneuse en ligne . Si vous êtes intéressé par les méthodes de rendu, plutôt que de générer le modèle, alors lisez mon cours sur l'infographie .

Exemple 3: ajout de contraintes

Revenons au tout premier exemple, et faisons exactement la même chose, mais ne réécrirons simplement pas les éléments du tableau sous les nombres 0, 18 et 31:

 import matplotlib.pyplot as plt x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. plt.plot(x, drawstyle='steps-mid') for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1])/2. plt.plot(x, drawstyle='steps-mid') plt.show() 

J'ai initialisé le reste, les éléments «libres» du tableau avec des zéros, et je les remplace toujours de manière itérative par la valeur moyenne des éléments voisins. Voici à quoi ressemble l'évolution du tableau dans les cent cinquante premières itérations:



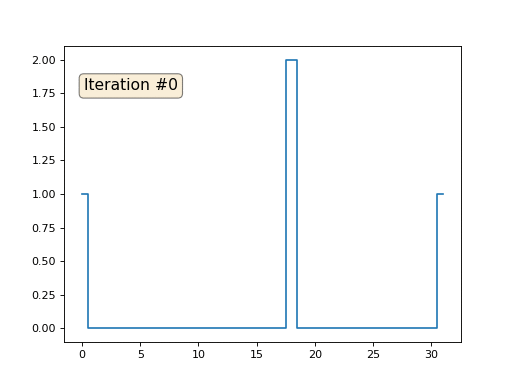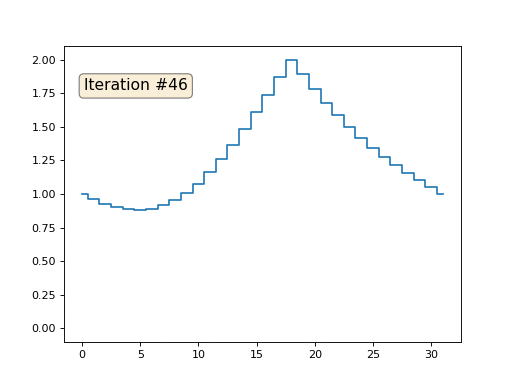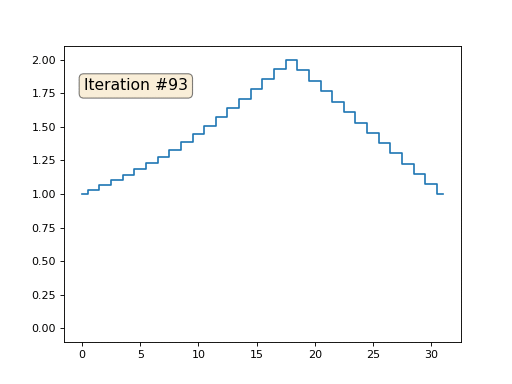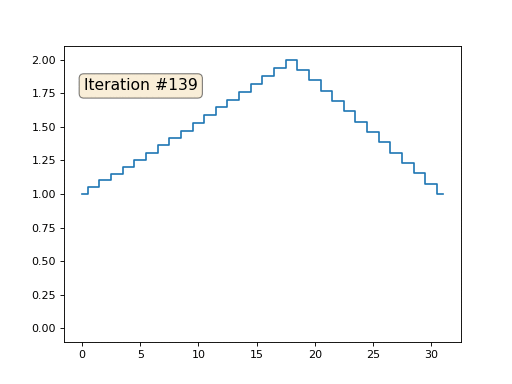
Il est bien évident que cette fois la solution convergera non pas vers un élément constant remplissant le réseau, mais vers deux rampes linéaires. Au fait, est-ce vraiment évident pour tout le monde? Sinon, expérimentez ce code, je donne spécifiquement des exemples avec un code très court afin que vous puissiez bien comprendre ce qui se passe.

Digression lyrique: solution numérique de systèmes d'équations linéaires.

Soit donné le système habituel d'équations linéaires:



Il peut être réécrit, en laissant dans chacune des équations d'un côté du signe égal x_i:



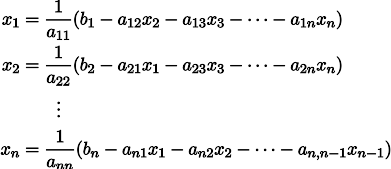
Soit un vecteur arbitraire approximation de la solution d'un système d'équations (par exemple, zéro).

Ensuite, en le collant dans le côté droit de notre système, nous pouvons obtenir un vecteur d'approximation de solution mis à jour .

Pour le rendre plus clair, x1 est obtenu à partir de x0 comme suit:



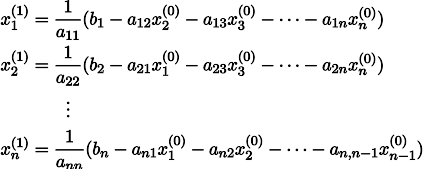
En répétant le processus k fois, la solution sera approximée par le vecteur

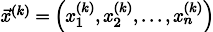
Soit au cas où, écrivez une formule de récursivité:



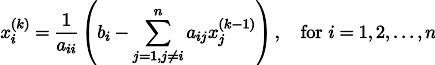
Sous certaines hypothèses sur les coefficients du système (par exemple, il est évident que les éléments diagonaux ne doivent pas être nuls, car nous les divisons), cette procédure converge vers la vraie solution. Cette gymnastique est connue dans la littérature sous le nom de méthode Jacobi . Bien sûr, il existe d'autres méthodes pour résoudre numériquement des systèmes d'équations linéaires, et des méthodes beaucoup plus puissantes, par exemple, la méthode du gradient conjugué , mais la méthode Jacobi est peut-être l'une des plus simples.

Exemple 3 à nouveau, mais d'autre part

Et maintenant, regardons de plus près la boucle principale de l'exemple 3:

 for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1])/2. 

J'ai commencé avec un vecteur x initial, et je le mets à jour mille fois, et la procédure de mise à jour est étrangement similaire à la méthode Jacobi! Écrivons ce système d'équations explicitement:



Prenez un peu de temps, assurez-vous que chaque itération dans mon code Python est strictement une mise à jour de la méthode Jacobi pour ce système d'équations. Les valeurs x [0], x [18] et x [31] sont fixes pour moi, respectivement, elles ne sont pas incluses dans l'ensemble de variables, elles sont donc transférées vers le côté droit.

Au total, toutes les équations de notre système ressemblent à - x [i-1] + 2 x [i] - x [i + 1] = 0. Cette expression n'est rien de plus que des différences finies ordinaires pour la dérivée seconde . Autrement dit, notre système d'équations prescrit simplement que la dérivée seconde doit être nulle partout (enfin, sauf au point x [18]). Rappelez-vous, j'ai dit qu'il est évident que les itérations doivent converger vers des rampes linéaires? C'est précisément pourquoi la dérivée linéaire de la dérivée seconde est nulle.

Savez-vous que nous venons de résoudre le problème de Dirichlet pour l'équation de Laplace ?

Soit dit en passant, un lecteur attentif aurait dû remarquer que, strictement parlant, dans mon code, les systèmes d'équations linéaires sont résolus non pas par la méthode Jacobi, mais par la méthode Gauss-Seidel , qui est une sorte d'optimisation de la méthode Jacobi:

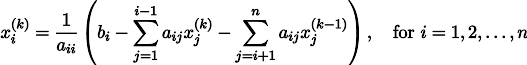
Exemple 4: équation de Poisson

Et changeons un peu le troisième exemple: chaque cellule est placée non seulement au centre de masse des cellules voisines, mais au centre de masse plus une constante (arbitraire):

 import matplotlib.pyplot as plt x = [0.] * 32 x[0] = x[31] = 1. x[18] = 2. plt.plot(x, drawstyle='steps-mid') for iter in range(1000): for i in range(len(x)): if i in [0,18,31]: continue x[i] = (x[i-1]+x[i+1] +11./32**2 )/2. plt.plot(x, drawstyle='steps-mid') plt.show() 

Dans l'exemple précédent, nous avons constaté que le placement au centre de masse est la discrétisation de l'opérateur de Laplace (dans notre cas, la dérivée seconde). Autrement dit, nous résolvons maintenant un système d'équations qui dit que notre signal doit avoir une dérivée seconde constante. La deuxième dérivée est la courbure de la surface; ainsi, une fonction quadratique par morceaux devrait être la solution à notre système. Vérifions l'échantillonnage dans 32 échantillons:



Avec une longueur de tableau de 32 éléments, notre système converge vers une solution en quelques centaines d'itérations. Mais que faire si nous essayons un tableau de 128 éléments? Tout est beaucoup plus triste ici, le nombre d'itérations doit déjà être calculé en milliers:



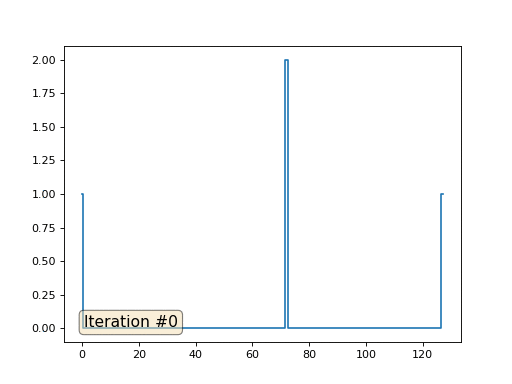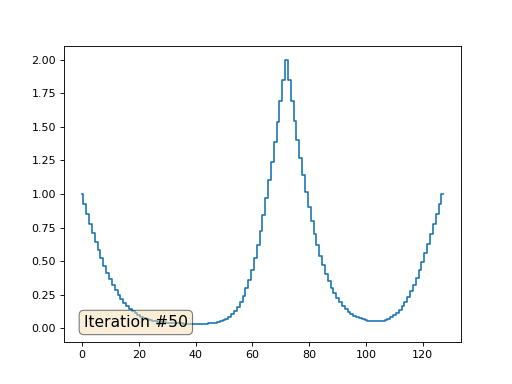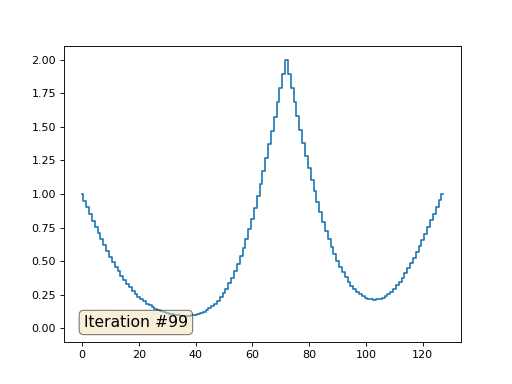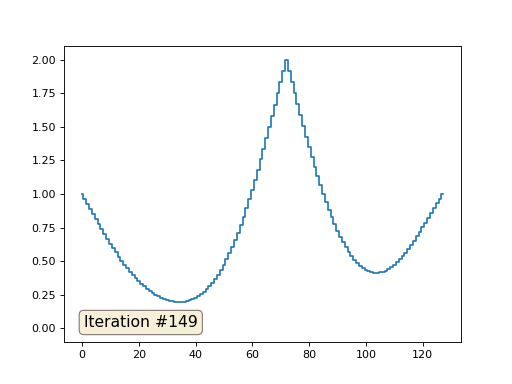
La méthode de Gauss-Seidel est extrêmement simple à programmer, mais ne s'applique pas aux grands systèmes d'équations. Vous pouvez essayer de l'accélérer, en utilisant, par exemple, des méthodes multigrilles . En mots, cela peut sembler lourd, mais l'idée est extrêmement primitive: si nous voulons une solution avec une résolution de mille éléments, nous pouvons d'abord résoudre avec dix éléments, obtenir une approximation approximative, puis doubler la résolution, la résoudre à nouveau, et ainsi de suite, jusqu'à ce que nous atteignions résultat souhaité. En pratique, cela ressemble à ceci:



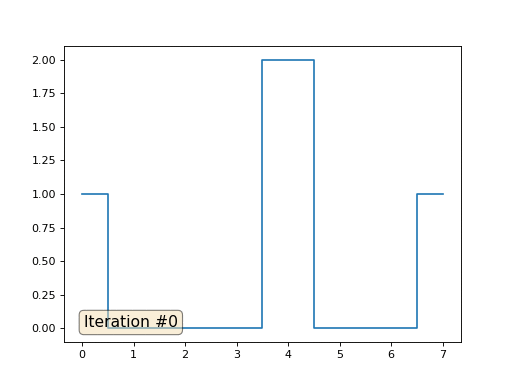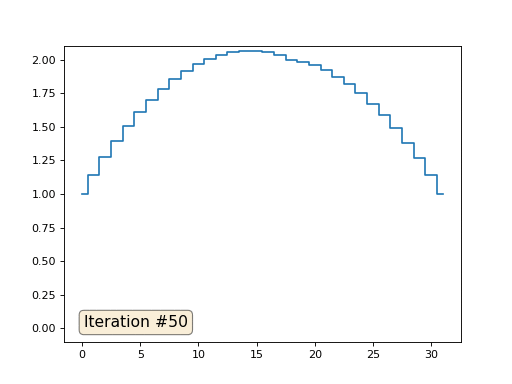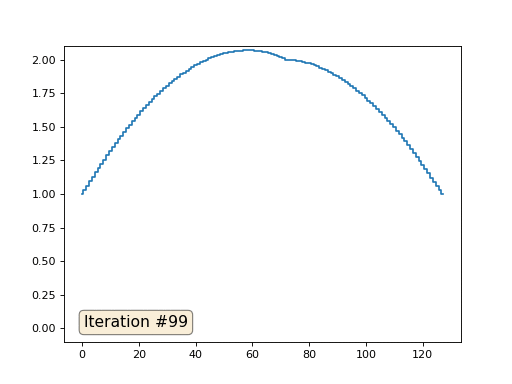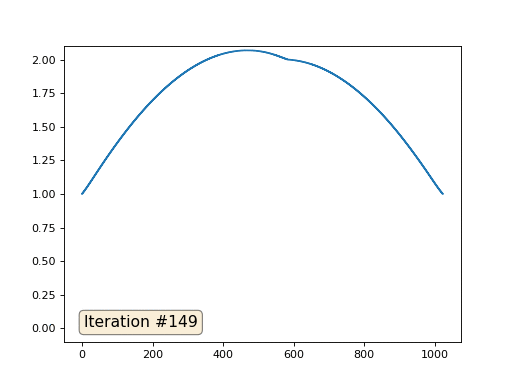
Et vous ne pouvez pas vous montrer et utiliser de vrais solveurs de systèmes d'équations. Je résous donc le même exemple en construisant la matrice A et la colonne b, puis en résolvant l'équation matricielle Ax = b:

 import numpy as np import matplotlib.pyplot as plt n=1000 x = [0.] * n x[0] = x[-1] = 1. m = n*57//100 x[m] = 2. A = np.matrix(np.zeros((n, n))) for i in range(1,n-2): A[i, i-1] = -1. A[i, i] = 2. A[i, i+1] = -1. A = A[1:-2,1:-2] A[m-2,m-1] = 0 A[m-1,m-2] = 0 b = np.matrix(np.zeros((n-3, 1))) b[0,0] = x[0] b[m-2,0] = x[m] b[m-1,0] = x[m] b[-1,0] = x[-1] for i in range(n-3): b[i,0] += 11./n**2 x2 = ((np.linalg.inv(A)*b).transpose().tolist()[0]) x2.insert(0, x[0]) x2.insert(m, x[m]) x2.append(x[-1]) plt.plot(x2, drawstyle='steps-mid') plt.show() 

Et voici le résultat du travail de ce programme, notez que la solution s'est avérée instantanément:



Ainsi, en effet, notre fonction est quadratique par morceaux (la dérivée seconde est constante). Dans le premier exemple, nous mettons la deuxième dérivée seconde à zéro, la troisième non nulle, mais la même partout. Et quel était le deuxième exemple? Nous avons résolu l' équation de Poisson discrète en spécifiant la courbure de la surface. Permettez-moi de vous rappeler ce qui s'est passé: nous avons calculé la courbure de la surface entrante. Si nous résolvons le problème de Poisson en fixant la courbure de la surface à la sortie égale à la courbure de la surface à l'entrée (const = 1), alors rien ne changera. Le renforcement des traits du visage se produit lorsque nous augmentons simplement la courbure (const = 2,1). Et si const <1, alors la courbure de la surface résultante diminue.

Mise à jour: un autre jouet comme devoirs

En développant l'idée suggérée par SquareRootOfZero , jouez avec ce code:



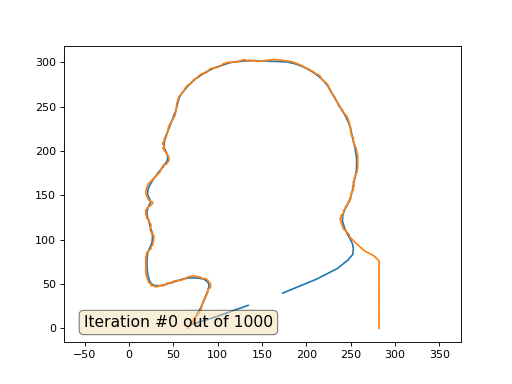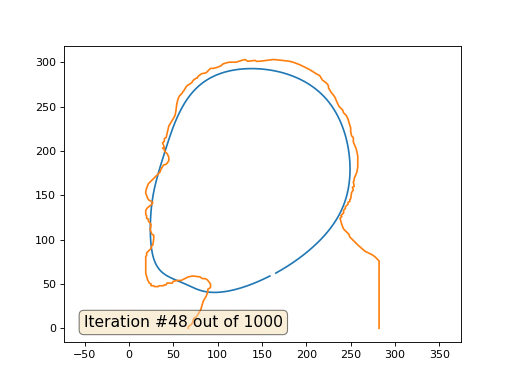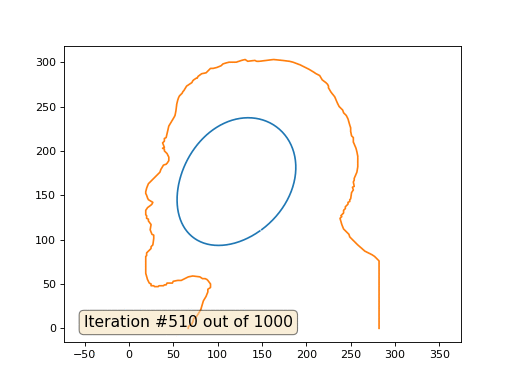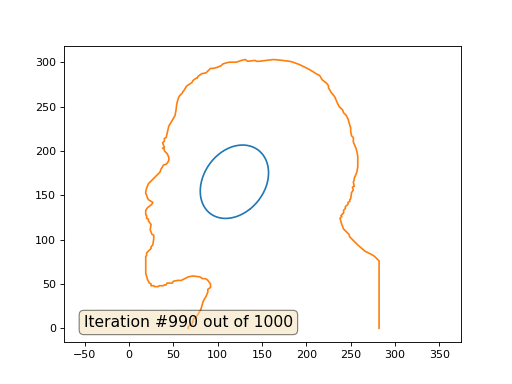
C'est le résultat par défaut, Lénine rouge est les données initiales, la courbe bleue est leur évolution, à l'infini le résultat converge en un point:



Et voici le résultat avec le coefficient 2:



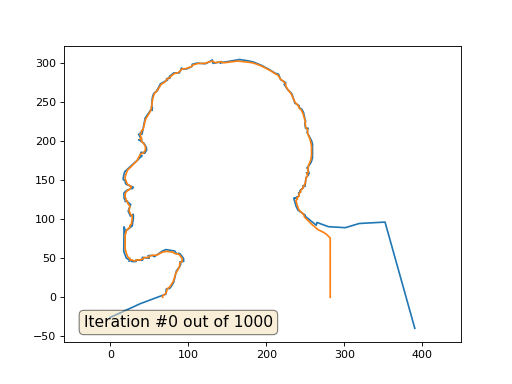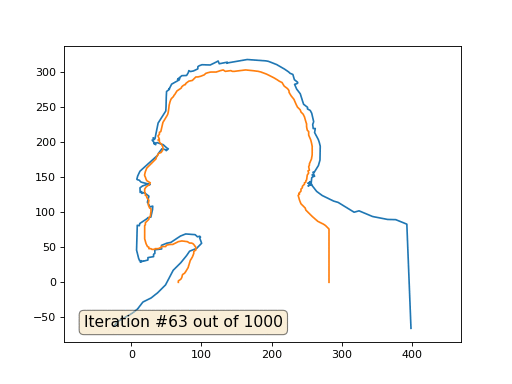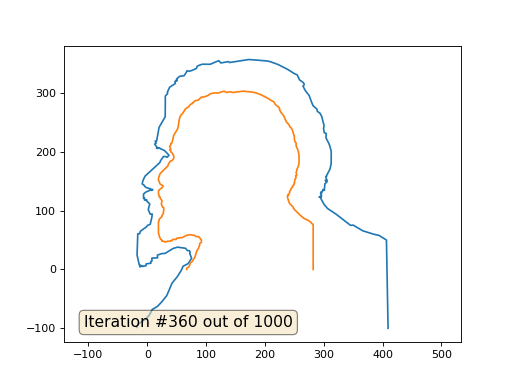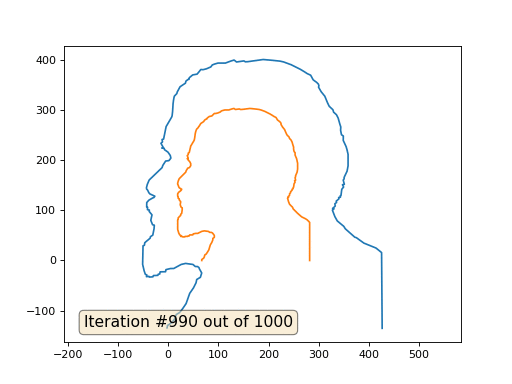
Devoirs: pourquoi dans le deuxième cas, Lénine se transforme d'abord en Dzerjinski, puis converge à nouveau vers Lénine, mais de plus grande taille?

Conclusion

De nombreuses tâches de traitement de données, en particulier la géométrie, peuvent être formulées comme une solution à un système d'équations linéaires. Dans cet article, je n'ai pas dit comment construire ces systèmes, mon objectif était seulement de montrer que c'est possible. Le sujet du prochain article ne sera plus «pourquoi», mais «comment» et quels solveurs utiliser plus tard.

Soit dit en passant, et après tout, dans le titre de l'article, il y a le moins de carrés. Les avez-vous vus dans le texte? Sinon, ce n'est absolument pas effrayant, c'est exactement la réponse à la question «comment?». Restez en ligne, dans le prochain article, je montrerai exactement où ils se cachent et comment les modifier pour accéder à un outil de traitement des données extrêmement puissant. Par exemple, en dix lignes de code, vous pouvez obtenir ceci:



Restez à l'écoute pour plus!