Il existe un certain nombre de tâches dans lesquelles un signal à long terme est divisé en segments, chacun étant traité séparément. En particulier, cette approche est utilisée pour analyser le signal en utilisant la transformée de Fourier de fenêtre, ou vice versa, dans la synthèse; ainsi que dans le traitement spectral tel que la suppression du bruit, le changement de tempo, le filtrage non linéaire, la compression des données audio et autres.

Le processus de partitionnement lui-même est représenté mathématiquement par la multiplication par une fonction de poids ( fenêtre ) avec un décalage. Pour la fenêtre la plus simple - rectangulaire - cela pourrait ressembler à ceci:

Signal source:



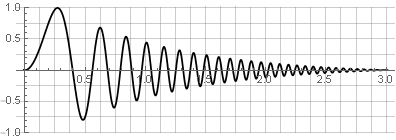
Cloisons:







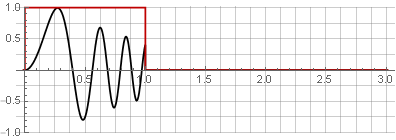
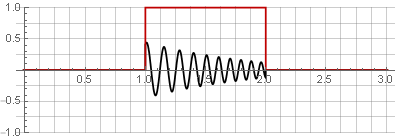
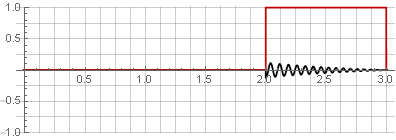
Vous pouvez restaurer le signal d'origine en les ajoutant simplement.

Plus de détails

Cependant par Pour un certain nombre de raisons, une fonction rectangulaire n'est pas la meilleure fonction de fenêtre. En analyse spectrale, à travers la transformée de Fourier discrète (généralement rapide), le bloc de données analysé semble "boucler", ce qui conduit à un écart aux bords et à une distorsion du spectre:



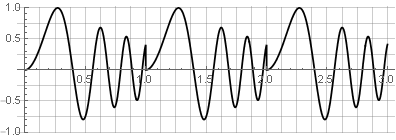
Il ne convient pas non plus à la synthèse inverse - car tout changement entraînera également des ruptures - par exemple, si nous essayons d'inverser l'une des parties:



Pour éliminer ces inconvénients, un chevauchement est utilisé - lorsque chaque fenêtre suivante capture une partie des données de la précédente; et la fenêtre de poids, respectivement, tombe progressivement sur les bords.

Chevauchement à 50%

Le plus souvent, ils utilisent la fenêtre Hannah (également appelée «cosinus surélevé») avec un chevauchement de 50%:








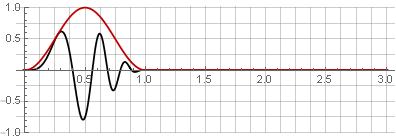
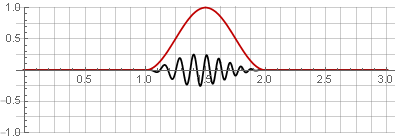
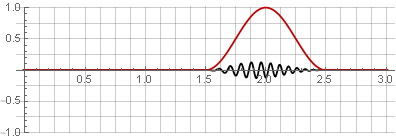
En raison de la symétrie de la fonction cosinus lors de l'addition, elles se résument à l'unité:



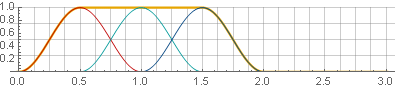
Maintenant, avec la synthèse inverse, nous n'obtiendrons pas de lacunes - mais seulement à condition qu'aux frontières de la fenêtre les valeurs iront toujours à zéro. Par exemple, lors de l'inversion d'une des pièces, le lissage ne sera pas violé:

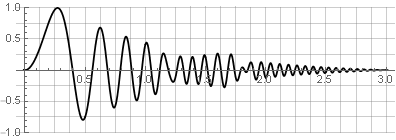
Traitement de double superposition

Considérons plus en détail l'algorithme de traitement d'un signal utilisant la transformée de Fourier rapide (FFT):

1. diviser le signal en segments avec une superposition de fenêtre;
2. FFT directe;
3. traitement du spectre;
4. FFT inverse;
5. superposition de fenêtres répétée (car après la FFT inversée, les bordures ne seront pas nécessairement ancrées à zéro sans se casser);
6. sommation des segments résultants.

De plus, si le traitement du spectre n'est pas effectué, le signal de sortie doit être identique au signal d'entrée (uniquement avec un retard inévitable).

Lorsque vous utilisez la fenêtre Hann, un chevauchement de 50% ne suffit plus, car des creux se produiront:



Étant donné que le double chevauchement équivaut à la quadrature, la solution évidente serait d'utiliser la racine de la fenêtre de Hann pour compenser la quadrature:



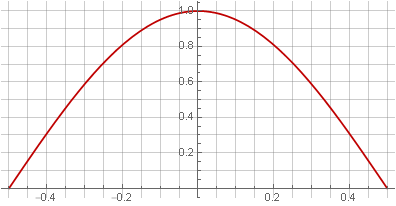
Dans ce cas, cependant, la fenêtre a cessé d'être lisse sur les bords - un écart est apparu dans la première dérivée.


Vous pouvez aller dans l'autre sens - utilisez le chevauchement de 75%, puis les fenêtres seront également additionnées en une constante - mais pas dans $$$1$ et $$$\ frac {3} {2}$ :



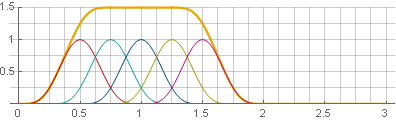
Dans ce cas, nous avons juste eu de la chance. Si nous développons le carré dans la somme, nous pouvons voir que c'est une composition de deux fenêtres Hannah, mais à des échelles différentes, ce qui nous permet de répondre aux exigences dont nous avons besoin:

$$

$$\ left (\ frac {\ cos (2 \ pi x) +1} {2} \ right) ^ 2 = \ frac {\ cos (2 \ pi x) +1} {2} + \ frac {\ cos (4 \ pi x) -1} {8}$$

Avec d'autres fonctions de fenêtre, une telle astuce ne fonctionnera pas; De plus, toutes les fonctions de fenêtre standard ne peuvent pas fournir une sommation dans une constante même avec un chevauchement de 50%.

Idée

Nous pouvons considérer la fenêtre de Hann non pas comme une fonction indépendante, mais comme la différence entre deux fonctions continues par morceaux (un article séparé a été consacré à une discussion détaillée à leur sujet) avec un décalage. Par exemple, en utilisant la fonction suivante

$$

$$\ left \ {\ begin {array} {ll} -1 & x \ leqslant -1 \\ 1 & x \ geqslant 1 \\ \ sin \ left (\ frac {\ pi x} {2} \ right) & -1 <x <1 \\ \ end {array} \ right.$$

peut écrire

$$

$$f (x + 1) -f (x-1)$$

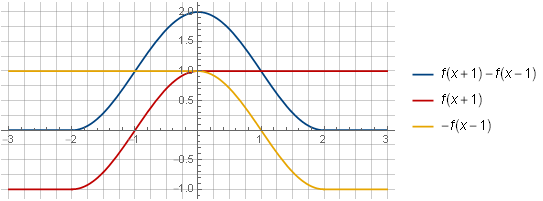
Après avoir considéré les composants de la somme de deux de ces fenêtres, leur capacité à résumer en une constante deviendra plus visuelle:



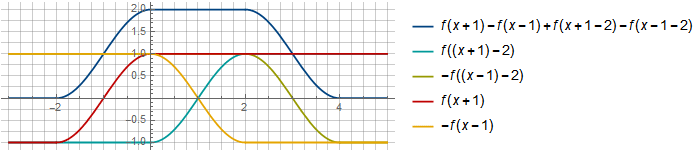
Sur le segment $$$[0,2]$ nous avons reçu une compensation mutuelle en plus des fonctions $$$-f (x-1)$ et $$$f ((x + 1) -2)$ depuis $$$f ((x + 1) -2) = f (x-1)$

Vous pouvez choisir un autre décalage, avec plus de chevauchement, par exemple:

$$

$$f \ left (x + \ frac {1} {2} \ right) -f \ left (x- \ frac {1} {2} \ right)$$

Et puis, lors du passage par étapes $$$\ frac {1} {2}$ , ils seront également résumés en une constante:



On peut voir que si vous réorganisez les composants de la fonction fenêtre, vous obtenez les mêmes fenêtres Hann.

Ainsi, en utilisant différentes fonctions de restriction, il est possible de former des fenêtres de la forme requise.

Formule finale

Maintenant, il ne reste plus qu'à définir l'échelle de sorte que les zones de définition et les valeurs ne dépendent pas de la quantité de chevauchement. Définition d'une fenêtre sur un intervalle $$$[0,1]$ nous obtenons

$$

$$\ frac {f \ left (\ frac {2 tx} {t-1} -1 \ right) -f \ left (\ frac {2 t (x-1)} {t-1} +1 \ right) } {2}$$

où $$$f$ - fonction continue par morceaux de la forme

$$

$$\ left \ {\ begin {array} {ll} -1 & x \ leqslant -1 \\ 1 & x \ geqslant 1 \\ g (x) & -1 <x <1 \\ \ end {array} \ à droite.$$

mais $$$g$ - une fonction d'interpolation entre les points $$$(- 1, -1)$ et $$$(1,1)$ .

Paramètre $$$t$ détermine le niveau de chevauchement - un diviseur qui détermine l'étape par laquelle chaque fenêtre suivante doit être décalée, $$$x_ {n + 1} = x_n + \ frac {1} {t}$ et doit être supérieur à un, $$$t> 1$ .

Pourcentage de chevauchement $$$p$ peut être calculé par la formule

$$

$$p = \ frac {100 (t-1)} {t}$$

et vice versa

$$

$$t = \ frac {100} {100-p}$$

L'aspect final de la fenêtre dépendra à la fois du choix du niveau de chevauchement et du choix de la fonction de limitation.

Quelques exemples intéressants

Nous allons voir ici quelques solutions toutes faites, pour lesquelles tout a commencé. Pour simplifier, nous considérons une fonction simplement interpolante $$$g (x)$ , sans autre cerclage.

Fenêtres polynomiales

Ils sont les moins chers en termes de calcul. Utilisation de la formule précédemment dérivée

$$

$$\ frac {2 x \ Gamma \ left (n + \ frac {1} {2} \ right) \, _2F_1 \ left (\ frac {1} {2}, 1-n; \ frac {3} {2} ; x ^ 2 \ droite)} {\ sqrt {\ pi} \ Gamma (n)}$$

on obtient un polynôme avec un nombre donné de zéros sur des dérivées supérieures qui assurent la douceur nécessaire de la fenêtre aux bords.


Avec un chevauchement de 75% de la fenêtre avec différentes valeurs de n, les fenêtres ressembleront à ceci:



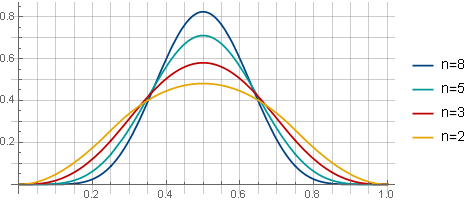
Et dans le cas de l'extraction de racine - comme ceci (lors de l'utilisation d'un chevauchement de 75%):



ou ainsi (lorsque vous utilisez un chevauchement de 50%):

La fenêtre la plus lisse

Fonction

$$

$$\ tanh \ left (\ frac {k x} {\ sqrt {1-x ^ 2}} \ right)$$

Il est intéressant en ce qu'il est infiniment différentiable et toutes ses dérivées aux bords sont 0 (ce qui peut être prouvé en considérant ses dérivées sur la base de règles de différenciation - dans chaque terme, il y aura un facteur de mise à zéro). Cela nous permet de construire des fenêtres sur sa base, dont toutes les dérivées n'ont pas de lacunes:

Vue de la fenêtre "jupe"

Le besoin de ce type de fenêtre est dû à l'augmentation de la résolution FFT, mais à la réduction de l'effet de «l'incertitude temps-fréquence» aux hautes fréquences en augmentant leur concentration au centre.

Tout d'abord, nous déterminons le type de fonction de fenêtre souhaité - par exemple, comme suit:

$$

$$- \ log \ left (k ^ 2 x ^ 2 + 1 \ right) + \ log \ left (k ^ 2 + 1 \ right) - \ frac {k ^ 2 \ left (1-x ^ 2 \ right) } {k ^ 2 + 1}$$

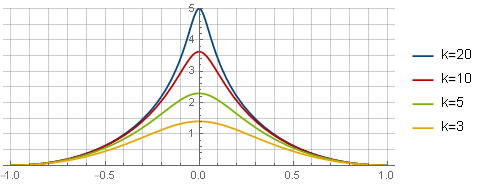
Ici, le premier terme détermine la forme de la fonction elle-même, le second - fournit l'intersection avec l'axe des abscisses, le troisième (parabole) réinitialise la dérivée sur les bords pour un ancrage en douceur; et le paramètre $$$k$ définit la "netteté" du pic. Sous cette forme, il n'est pas encore utilisable - vous devez d'abord en obtenir la fonction de restriction via l'intégration et la mise à l'échelle:

$$

$$\ frac {kx \ left (k ^ 2 \ left (x ^ 2 + 3 \ right) +6 \ right) +3 \ left (k ^ 2 + 1 \ right) \ left (kx \ left (\ log \ gauche (k ^ 2 + 1 \ droite) - \ log \ gauche (k ^ 2 x ^ 2 + 1 \ droite) \ droite) -2 \ tan ^ {- 1} (kx) \ droite)} {4 k ^ 3-6 \ gauche (k ^ 2 + 1 \ droite) \ tan ^ {- 1} (k) +6 k}$$

Pour plus de commodité, vous pouvez lier le paramètre $$$k$ au niveau du chevauchement $$$t$ - par exemple, de sorte que la 4ème dérivée au centre de la fenêtre soit 0 - puis $$$k$ sera considéré comme $$$\ sqrt {3} (t-1)$ :



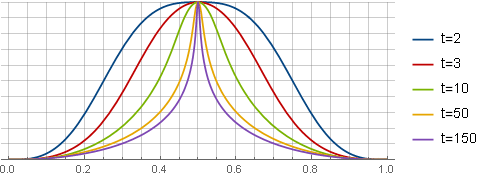
Ici, pour plus de clarté, toutes les fenêtres sont réduites à la même échelle.

Fenêtre de vue d'aiguille

Il s'agit d'une version plus «agressive» de la fenêtre précédente. Une hyperbole a été choisie comme base, à partir de laquelle, par des transformations successives

$$

$$\ frac {1} {x} \ to \ frac {1} {\ sqrt {x ^ 2}} \ to \ frac {1} {\ sqrt {x ^ 2 + 1}} \ to \ frac {1} {\ sqrt {k ^ 2 x ^ 2 + 1}} \ to \ frac {\ left (1-x ^ 2 \ right) ^ 2} {\ sqrt {k ^ 2 x ^ 2 + 1}}$$

et en utilisant les mêmes étapes sous forme d'intégration et de mise à l'échelle a obtenu la formule

$$

$$\ frac {kx \ left (2 k ^ 2 \ left (x ^ 2-4 \ right) -3 \ right) \ sqrt {k ^ 2 x ^ 2 + 1} + \ left (8 \ left (k ^ 4 + k ^ 2 \ droite) +3 \ droite) \ sinh ^ {- 1} (kx)} {\ gauche (8 \ gauche (k ^ 4 + k ^ 2 \ droite) +3 \ droite) \ sinh ^ {-1} (k) -3 k \ sqrt {k ^ 2 + 1} \ gauche (2 k ^ 2 + 1 \ droite)}$$

Ici, vous pouvez également lier le paramètre $$$k$ au niveau du chevauchement. La solution directe de l'équation de la dérivée 4 donne un résultat encombrant, il suffit donc de faire l'image de la fenêtre précédente dans l'image et la ressemblance en définissant $$$k$ comment $$$k (t-1)$ assurant ainsi le rôle du paramètre $$$k$ comme "réglage fin". À $$$k = 2,22$ les fenêtres ressembleront à ceci:

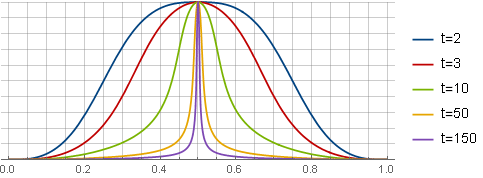
Fenêtre asymétrique

La fonction de fenêtre ne doit pas du tout être symétrique. Disons que nous avons besoin d'une fenêtre avec une attaque nette et une atténuation douce. Nous pouvons l'obtenir selon un schéma déjà familier - déterminer d'abord la forme souhaitée de la fonction, puis par intégration, nous obtenons la fonction de restriction. Ici, la tâche est légèrement plus compliquée du fait que, en raison de l'asymétrie, le centre ne passera plus par l'origine, donc une étape de calcul supplémentaire est ajoutée. Cela conduit également au fait que les formules en conséquence sont plutôt lourdes. Par exemple, considérons l'option la plus simple - une parabole multipliée par une fenêtre de poids polynomial:

$$

$$(1-x) ^ 2 \ gauche (1-x ^ {10} \ droite) ^ 2$$

Ici, le degré de x dans la fenêtre pondérée (à savoir 10) détermine la «netteté» de l'attaque. Nous avons utilisé une valeur spécifique, plutôt qu'un paramètre symbolique, pour simplifier les formules pour plus de clarté - si vous le souhaitez, vous pouvez le recalculer plus tard.

Après l'intégration, la simple mise à l'échelle ne suffit plus - vous devez toujours aligner les bords:



Pour ce faire, nous décalons d'abord la fonction vers le haut pour aligner le bord gauche, puis la redimensionnons aux deux sur le bord droit et soustrayons un. Ensuite, nous obtenons la formule suivante:

$$

$$\ frac {8775 \ left (\ frac {x ^ {27}} {27} - \ frac {2 x ^ {26}} {26} + \ frac {x ^ {25}} {25} - \ frac {2 x ^ {15}} {15} + \ frac {4 x ^ {14}} {14} - \ frac {2 x ^ {13}} {13} + \ frac {x ^ 3} {3} -x ^ 2 + x + \ frac {117592} {61425} \ droite)} {9856} -1$$

Pour que la fenêtre finale ait l'apparence souhaitée, il est également nécessaire de prévoir un niveau de chevauchement suffisamment important:

Conclusion

De même, vous pouvez créer des fenêtres à partir de toutes les autres fonctions en forme de cloche - par exemple, les gaussiens; et vous pouvez également modifier ceux déjà considérés pour fournir une plus grande fluidité ou changer la forme de la courbe.

Par considération, la composition spectrale de ces fonctions de fenêtre est restée - des études distinctes devraient y être consacrées.

Une version légèrement plus avancée de l'article (avec la possibilité de modifier dynamiquement les paramètres dans les fenêtres considérées et les formules cachées) sous la forme d'un document Wolfram Mathematica peut être téléchargée ici .