De combien de programmeurs avez-vous besoin pour prendre en charge du code précédemment écrit?

Il y a quelque temps, une conversation a eu lieu entre moi et mon bon ami, dans laquelle les phrases suivantes sonnaient:

- Le nombre de programmeurs augmentera constamment - car la quantité de code augmente, et de plus en plus de développeurs sont constamment tenus de le prendre en charge.
- Mais le code vieillit, une partie quitte le support. La présence d'une sorte d'équilibre n'est pas exclue.

En les rappelant quelques jours plus tard, je me demandais si le support du code, nécessitant de plus en plus de ressources au fil du temps, pourrait finalement paralyser le développement de nouvelles fonctionnalités, ou nécessiterait une augmentation illimitée du nombre de programmeurs? L'analyse mathématique et les équations différentielles ont aidé à évaluer qualitativement la dépendance du volume de soutien au développement et à trouver des réponses aux questions.

La première question. Le soutien peut-il «manger» toutes les ressources de développement?

Considérons une équipe de programmeurs dans laquelle le nombre de participants est constant. Part de leur temps de travail $$$\ mu (t)$ ( $$$0 <\ mu (t) <1$ ) expliquée par l’élaboration d’un nouveau code et le reste du temps $$$1- \ mu (t)$ va au support. Selon les hypothèses du modèle, supposons que le premier type d'activité vise à augmenter la quantité de code, et le second - à le changer (correction des erreurs) et n'affecte pas de manière significative la quantité de code.

Nous dénotons $$$y (t)$ tout le code écrit par le temps $$$t$ . Considérant que la vitesse d'écriture du code est proportionnelle $$$\ mu (t)$ nous obtenons:

$$

$$\ frac {dy (t)} {dt} = a_0 \ mu (t); a_0 \ in \ mathbb {R}, a_0> 0.$$

Il est naturel de supposer que le travail impliqué dans le maintien du code est proportionnel à son volume:

$$

$$1- \ mu (t) = a_1 y (t); a_1 \ in \ mathbb {R}, a_1> 0$$

ou

$$

$$\ mu (t) = 1-a_1y (t)$$

D'où

$$

$$\ frac {dy (t)} {dt} = a_0 (1-a_1y (t))).$$

Nous obtenons une équation différentielle qui s'intègre facilement. Si au moment initial la quantité de code est nulle, alors

$$

$$y (t) = \ frac {1} {a_1} (1-e ^ {- a_0a_1t}).$$

À $$$t \ à + \ infty$ fonction $$$y (t) \ to1 / a_1$ et $$$\ mu (t) \ à 0$ . Et cela signifie une réduction progressive au fil du temps du développement de nouvelles fonctionnalités à zéro et la transition de toutes les ressources vers le support.

Cependant, si à temps $$$h> 0$ Étant donné que le code devient obsolète et cesse d'être pris en charge, la quantité de code nécessitant une prise en charge à la fois $$$t$ égal à $$$y (t) - y (t-h).$ Alors

$$

$$1- \ mu (t) = a_1 (y (t) - y (t-h)),$$

$$

$$\ mu (t) = 1-a_1 (y (t) - y (t-h)),$$

mais $$$y (t)$ est une solution d'une équation différentielle avec un argument retardé [1]:

$$

$$\ frac {dy (t)} {dt} = a_0 (1-a_1 (y (t) - y (t-h))).$$

La solution de cette équation est uniquement déterminée en définissant les valeurs $$$y (t)$ "Avant le commencement des temps", avec $$$t \ in [-h, 0]$ . Puisqu'aucun code n'a été écrit avant l'heure initiale, dans notre cas $$$y (t) = 0$ à $$$t \ in [-h, 0]$ .

Regardons quelques exemples. Nous mesurerons le temps en années et la quantité de code en milliers de lignes. Alors pour $$$a_0$ Des valeurs de l'ordre de dizaines sont acceptables, nous prenons 50 et 100. C'est-à-dire que dans un an, l'équipe de développement écrira respectivement cinquante et cent mille lignes de code. Pour $$$a_1$ les valeurs acceptables peuvent être: $$ , $$ , $$ . Cela signifie que l'équipe de développement est en mesure de maintenir la quantité de code qu'elle a écrite pour l'année, avec un quart, la moitié ou la charge de travail complète. Comme durée de vie moyenne du code, définissons les valeurs: 1, 2 et 4 ans. En résolvant l'équation numériquement, nous obtenons des exemples du comportement de la fonction $$$\ mu (t)$ pour certaines combinaisons de paramètres $$$h, a_0, a_1$ .

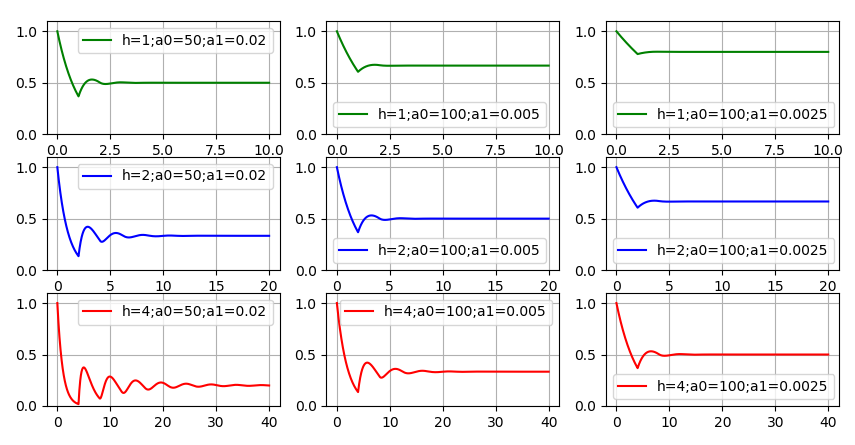
Comportement des fonctions $$$\ mu (t)$ face au vieillissement du code a changé. La fonction a cessé d'être monotone, mais les fluctuations «se calment» avec le temps, il y a une tendance à $$$\ mu (t)$ à une valeur constante. Les graphiques montrent: plus $$$h$ , $$$a_0$ et $$$a_1$ , c'est-à-dire que plus le code vieillit lentement, plus le développement de nouveau code se produit rapidement et plus la qualité du code est faible, moins il restera de ressources pour le développement de nouvelles fonctionnalités. Il y avait un désir de donner au moins un exemple dans lequel $$$\ mu (t)$ "Blotti" près de zéro. Mais cela a nécessité la sélection d'indicateurs de qualité du développement très médiocres et d'un code vieillissant. Même dans le graphique inférieur gauche, une quantité importante de ressources reste pour la nouvelle fonctionnalité. Par conséquent, la bonne réponse à la première question est plus probable: théoriquement - oui, c'est possible; pratiquement - à peine.

Questions sans réponse:

1. Est-il vrai que $$$\ mu (t)$ tend à une certaine limite pour $$$t \ à + \ infty$ pour tous $$$a_0, a_1> 0$ ? Si ce n'est pas pour tout le monde, alors pour qui?
2. Si la limite existe, alors comment sa valeur dépend $$$a_0, a_1$ ?

La deuxième question. La prise en charge du code peut-elle entraîner une croissance illimitée du nombre de programmeurs?

Nous dénotons $$$q (t)$ nombre de programmeurs impliqués dans le développement d'un nouveau code. Comme ci-dessus $$$y (t)$ - la quantité de code écrit par le temps $$$t$ . Alors

$$

$$\ frac {dy (t)} {dt} = a_2 q (t); a_2 \ in \ mathbb {R}, a_2> 0.$$

Laissez le support du code occupé $$$p (t)$ programmeurs. Vieillissement du code C

$$

$$p (t) = a_3 (y (t) -y (t-h)); a_3 \ in \ mathbb {R}, a_3> 0.$$

D'où

$$

$$p (t) = a_3 \ int_ {t-h} ^ {t} \ frac {dy (s)} {ds} ds = a_2a_3 \ int_ {t-h} ^ tq (s) ds.$$

Si $$$q (t) \ leq C_1$ alors

$$

$$p (t) \ leq a_1a_2C_1h.$$

Ainsi, la réponse à la deuxième question est négative: si le nombre de développeurs de nouveau code est limité, alors dans le contexte du vieillissement du code, le support ne peut pas provoquer une augmentation illimitée du nombre de programmeurs.

Conclusion

Les modèles considérés sont des modèles mathématiques «mous» [2]. Ils sont très simples. Néanmoins, la dépendance des résultats de simulation sur les valeurs des paramètres correspond à celle attendue pour les systèmes réels, ce qui plaide en faveur de l'adéquation des modèles et d'une précision suffisante pour obtenir des estimations qualitatives.

Les références

1. Elsgolts L.E., Norkin S.B. Introduction à la théorie des équations différentielles avec argument déviant. Moscou Maison d'édition "Science". 1971.
2. Arnold V.I. Modèles mathématiques "durs" et "mous". Moscou Maison d'édition du Centre. 2004.