Le nouveau modèle statistique semble saper les hypothèses acceptées depuis longtemps par la théorie des nombres. Jusqu'à quel point pouvez-vous lui faire confiance si seules des preuves rigoureuses comptent vraiment?
Récemment, quatre chercheurs ont mis au point un modèle qui bouleverse tout le bon sens de leur domaine de recherche. Ils ont utilisé des données informatiques pour suggérer que la vision dominante de plusieurs décennies d'un des concepts fondamentaux était erronée.
Et ce ne sont pas des biologistes, des climatologues ou des physiciens. Dans leur domaine scientifique, les modèles empiriques n'ont pas leur mot à dire sur la vérité. Ce sont des mathématiciens, représentants de la discipline, dont la monnaie courante - une preuve logique indéniable - les sauve généralement des débats qui touchent d'autres domaines. Et pourtant, ils sont là, avec leur modèle disant qu'il est probablement temps de réviser certaines des idées de longue date.
Un modèle
publié en ligne en 2016 et prêt à paraître dans le Journal of the European Mathematical Society appartient à un concept mathématique aussi vénérable que le rang d'une équation algébrique. Le rang est une mesure correspondant au nombre de solutions de l'équation liées à des nombres rationnels et à celles irrationnelles. Les équations de haut rang ont des solutions plus rationnelles et sont plus compliquées.
Depuis le début du XXe siècle, les mathématiciens se sont intéressés à la question de savoir s'il existe des restrictions sur la hauteur du rang de l'équation. Au début, presque tout le monde pensait que la restriction devait exister. Mais dans les années 1970, l'opinion dominante avait changé - la plupart des mathématiciens ont commencé à croire que le rang était illimité, ce qui signifie qu'il est possible de détecter des courbes avec des rangs infiniment grands. C'est ce qui s'est passé, même si certains mathématiciens pensaient qu'il n'y avait pas d'arguments solides à l'appui de cette opinion.
«Les gens sont très autoritaires quant à l'absence de restrictions. Cependant, lorsque vous commencez à comprendre, il s'avère que les preuves en sont extrêmement faibles », a déclaré
Andrew Granville , mathématicien à l'Université de Montréal et à l'University College London.
Aujourd'hui, les preuves suggèrent le contraire. Deux ans après l'apparition du modèle, elle a convaincu de nombreux mathématiciens que le rang des équations algébriques d'un certain type était vraiment limité. Cependant, tout le monde ne pense pas que ce modèle soit convaincant. Le manque d'accord soulève des questions qui ne sont pas souvent liées aux résultats mathématiques - quel poids les preuves empiriques peuvent-elles avoir dans un domaine où seule une preuve rigoureuse compte?
"Il n'y a aucune justification mathématique que ce modèle est exactement ce dont nous avons besoin", a déclaré
Jennifer Park , mathématicienne à l'Université de l'Ohio, co-auteur de l'ouvrage. «De plus, d'un point de vue expérimental, beaucoup de choses fonctionnent.»
Point à point
Si vous obtenez une équation, vous pouvez tracer une courbe de ses solutions sur le graphique. Les mathématiciens veulent savoir combien de ces solutions sont rationnelles - elles appartiennent au type de nombres, qui peut être exprimé comme le rapport de deux entiers (1/2, -3 ou 4483/929).
Les solutions rationnelles sont difficiles à trouver systématiquement, mais les mathématiciens ont des techniques qui fonctionnent dans certaines conditions. Prenez l'équation x
2 + y
2 = 1. Le graphique des solutions à cette équation est un cercle. Pour trouver tous les points rationnels du cercle, nous commençons par une solution définie - disons, à partir du point où x = 1 et y = 0. Tracez ensuite une ligne passant par ce point qui coupe le cercle à un autre point. Si la pente de notre droite est rationnelle, le deuxième point d'intersection sera également une solution rationnelle. En traçant une ligne, nous avons augmenté le nombre de décisions rationnelles de une à deux.
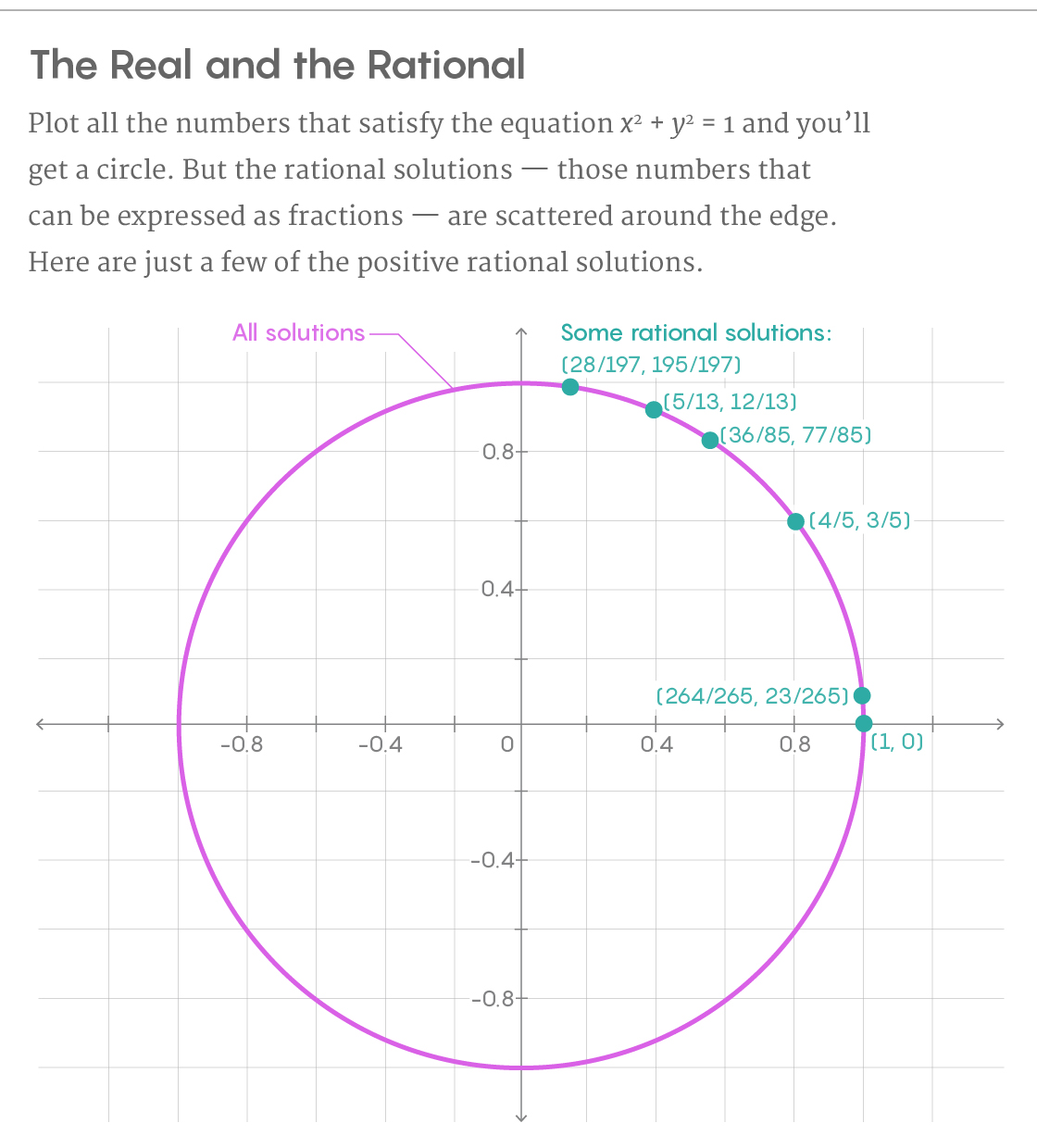
Et il n'est pas nécessaire de s'arrêter là. Nous répétons la procédure en traçant une ligne droite avec une autre pente rationnelle à travers le deuxième point rationnel - elle coupe le cercle au troisième point rationnel. En poursuivant vers l'infini, nous trouverons éventuellement tous les points rationnels du cercle, dont il existe un nombre infini.
Et dans le cas d'un cercle, vous devez partir d'un seul point, et vous pouvez tous les trouver. Le nombre de décisions rationnelles que vous devez connaître au début afin de trouver toutes les autres est connu comme le rang de la courbe. Le rang est une manière ordonnée de décrire un ensemble infini de décisions rationnelles en un seul nombre. "C'est un peu comme la meilleure façon de décrire les solutions rationnelles à ces courbes", a déclaré
Bjorn Puunen , mathématicien au MIT, co-auteur du modèle, avec Park,
John Voight du Dartmouth College et
Melanie Matchet Wood de l'Université du Wisconsin.
Un cercle est une équation quadratique ou une équation du deuxième degré («degré» signifie la grandeur du plus grand des degrés des termes de l'équation). Depuis plus de cent ans, les mathématiciens savent trouver des solutions rationnelles aux équations du deuxième degré.
Les équations de type suivant sont les courbes elliptiques, dans lesquelles il y a des variables élevées au troisième degré. Les courbes elliptiques existent dans le domaine le plus attractif de la recherche mathématique. Ils sont plus compliqués que les équations du second ordre, ils sont donc intéressants à étudier, mais ils ne sont pas trop compliqués. La procédure modifiée pour tracer des lignes droites est toujours applicable aux courbes elliptiques, mais cesse de fonctionner avec des équations du quatrième ordre et plus.
Les courbes elliptiques sont de rangs différents. Avec certaines courbes elliptiques, vous pouvez partir d'un point rationnel, appliquer la procédure de tracé de lignes et ne pas trouver toutes les solutions rationnelles. Vous devrez peut-être ajouter un deuxième point rationnel qui n'est pas lié au premier. Avec lui, vous commencerez une nouvelle procédure pour tracer des lignes, et vous trouverez un équilibre de points rationnels. Une courbe, pour trouver tous les points rationnels dont vous devez d'abord connaître deux points rationnels, a un rang égal à deux.
Il n'y a aucune restriction prouvée sur la hauteur du rang d'une courbe elliptique. Plus le rang de l'équation est élevé, plus l'ensemble des solutions rationnelles de la courbe est large et complexe. "Le classement mesure en quelque sorte la complexité de l'ensemble des décisions", a déclaré Puunen.
Néanmoins, le rang échappe aux tentatives des mathématiciens de le décrire en théorie. Si vous obtenez une courbe elliptique, elle n'aura pas de relation évidente entre son apparence et son rang. "Si j'ai une courbe elliptique et que j'ajuste un peu les coefficients, alors son rang change radicalement", a déclaré Park. - Vous pouvez changer le coefficient d'un, et le rang passera à un million. Personne ne sait comment se comportent les rangs. »
L'absence d'une théorie générale a conduit les mathématiciens à se replier sur le petit ensemble de preuves dont ils disposent pour spéculer sur l'existence d'une restriction de rang. "Le point de vue est qu'il n'y a pas de restrictions sur le grade, car les gens ont toujours trouvé des rangs de plus en plus élevés", a expliqué Granville. Le détenteur du record actuel est une courbe elliptique de rang 28, découverte en 2006 par Noam Elkis, mathématicien à l'Université de Harvard.
Mais alors ce nouveau modèle est apparu, et a déclaré que c'était presque certainement la fin de la route.
Surprise vers 21 ans
Pour étudier des phénomènes trop complexes ou inaccessibles à la recherche directe, les scientifiques utilisent des modèles. Ayant créé un analogue d'un trou noir dans le laboratoire, ils peuvent être en mesure d'apprendre quelque chose sur le comportement des vrais trous noirs, sans avoir à marcher le long de l'horizon des événements.
Les mathématiciens font de même. Un bon exemple est l'étude des nombres premiers. Les mathématiciens veulent connaître la réponse à la question
des nombres premiers jumeaux - existe-t-il un nombre infini de paires de nombres premiers qui diffèrent de 2 (3 et 5, 11 et 13). Une réponse exhaustive va au-delà de leurs connaissances, mais ils ont créé des modèles qui prédisent la fréquence des nombres jumeaux - et la réponse semble être qu'ils se produisent un nombre infini de fois.
Le nouveau modèle n'étudie pas directement les courbes elliptiques elles-mêmes. Elle explore un objet mathématique tel que
le noyau de la matrice . Les noyaux se réfèrent à des courbes elliptiques, comme les souris pour les gens ne sont pas la même chose, mais ils sont plus faciles à étudier, et on espère qu'ils sont suffisamment proches pour tirer des conclusions sur certains sur la base d'expériences sur d'autres. En particulier, les noyaux ont leur propre version du
rang . Après avoir étudié la distribution du rang des noyaux - combien de noyaux ont un rang de 1, combien de noyaux ont un rang de 2, et ainsi de suite - quatre mathématiciens espéraient avoir une idée de la distribution des rangs des courbes elliptiques. En fait, ils parient que la distribution des rangs des noyaux et des courbes elliptiques est similaire.
 Jennifer Park, Bjorn Puunen et Melanie Wood
Jennifer Park, Bjorn Puunen et Melanie Wood"L'acte de foi entre en jeu", a déclaré Park. "Nous espérons qu'il existe peut-être un autre ensemble d'objets mathématiques qui est beaucoup plus compréhensible et a la même distribution de rang que les courbes elliptiques."
Lorsque les quatre chercheurs ont fait ce travail, la plupart des mathématiciens considéraient le rang comme illimité. Cependant, le modèle a raconté une histoire différente. Elle dit qu'il n'y a qu'un nombre fini de courbes elliptiques avec un rang supérieur à 21. Et s'il y en a un nombre fini, alors l'une d'entre elles aura le rang le plus élevé - ce qui signifie que le rang a toujours une limite supérieure. Lorsque les quatre mathématiciens ont vu cela, ils ont réalisé qu'ils avaient un résultat vivant entre leurs mains.
"Cette prédiction ne correspondait pas à ce que tout le monde croyait, du moins ce qu'ils ont publiquement admis", a déclaré Wood. "Personne ne croyait que les rangs pouvaient avoir une limitation."
Si la foi dans le modèle nécessite une étape assez sérieuse, alors lorsque le modèle signale que le bon sens était faux, une étape encore plus grande est requise. Cependant, de nombreuses preuves plaident en faveur de ce résultat. Ce modèle est basé sur des modèles précédents créés par d'autres mathématiciens qui ont étudié diverses propriétés des courbes elliptiques. Ces modèles ont résisté à l'épreuve du temps; certaines de ces prédictions ont même été prouvées.
"Personne n'a suggéré de partir de zéro et de créer un nouveau modèle", a déclaré Wood. «La question était de savoir comment enrichir les modèles existants auxquels les gens croient déjà.»
Une autre raison de croire au modèle était qu'une valeur de rang de 21 ne semble pas être une frontière arbitraire. Dix ans plus tôt, Granville a créé un autre modèle, dont il s'ensuit également qu'il ne devrait y avoir qu'un nombre limité de courbes elliptiques avec un rang supérieur à 21. Le modèle de Granville n'était pas du tout similaire au modèle actuel - et le fait que tous deux aient donné le rang 21 comme significatif était contrairement à une simple coïncidence du point de vue de nombreux mathématiciens.
"Nous avons deux modèles heuristiques complètement différents et les deux ont donné le même nombre, 21 - cela a surpris les gens", a déclaré Park.
La raison la plus convaincante pour laquelle le modèle semble crédible est peut-être le fait que ses autres prédictions correspondent presque exactement aux propriétés prouvées des courbes elliptiques. La conclusion généralisée du modèle - l'existence d'un nombre fini de courbes elliptiques avec un rang supérieur à 21 - s'applique à toutes les courbes elliptiques. Cependant, ils ont certaines familles, pour beaucoup desquelles les mathématiciens ont déjà déterminé les limites des rangs. Le modèle a également prédit des valeurs de rang pour bon nombre de ces familles, et ses prédictions étaient similaires, voire coïncidaient exactement avec les limites que les mathématiciens ont déjà déterminées.
"Nos frontières ont prédit avec précision tous ces cas qui ont été étudiés par d'autres personnes", a déclaré Park. "Les gens sont sceptiques quant à mes rapports, mais quand je mentionne d'autres coïncidences, ils en sont très surpris."
Entre preuve et preuve
Le modèle a beaucoup de soutien, mais tout le monde ne le croit pas et il peut s'avérer faux. Le sceptique le plus important est Noam Elkis, un mathématicien de Harvard qui a établi un record de classement pour une courbe elliptique. Depuis qu'il est devenu le plus jeune professeur à temps plein à Harvard, il a reçu plusieurs résultats indiquant l'absence de limite de rang. "Mon opinion n'a pas changé depuis longtemps - je ne pense pas que nous connaissions bien cette question pour soutenir telle ou telle hypothèse", m'a écrit Elkis par mail.
Elkis estime que le modèle peut ne pas fonctionner correctement à bien des égards. Il prend en compte les courbes sélectionnées au hasard, ou les courbes dans un certain sens sont moyennes. Cependant, il existe des preuves, y compris des recherches par Elkis lui-même, sur la possibilité de l'existence de familles de courbes elliptiques, chacune comprenant un nombre infini de telles courbes, dont le comportement diffère considérablement du comportement des courbes typiques. «Les modèles heuristiques basés sur le comportement attendu des courbes aléatoires peuvent ne pas raconter toute l'histoire d'un comportement extrême», écrit Elkis.
Même l'un des auteurs du modèle n'en est pas complètement sûr. "Je dirais que je suis limité dans les rangs comme un agnostique", a déclaré Wood. Elle admet que le modèle peut être incorrect pour des raisons exprimées par Elkis. Mais si le modèle ne fait pas face à la tâche, alors parce qu'il n'a pas pris en compte certaines propriétés cachées et inattendues des courbes elliptiques. "La question est: si vous ne croyez pas aux rangs limités, à quel endroit le modèle cesse-t-il de fonctionner?" - dit Wood.
«Très probablement, ils auront raison si quelqu'un ne trouve pas une raison ingénieuse pour laquelle ils ont tort. Je ne sais pas si une telle raison existe ou non », a déclaré Alexander Smith, un étudiant diplômé de Harvard travaillant avec Elkis et étudiant les rangs des courbes elliptiques.
Les auteurs du modèle n'élèvent pas sa signification au dogme. Ils connaissent la différence entre l'évidence et l'évidence, et ils comprennent qu'aucune montagne de la première ne mènera à la seconde. Mais ils estiment que leur travail, à tout le moins, fournit une base raisonnable de réflexion sur les concepts mathématiques de base après un siècle de raisonnement simple.
"Peut-être que trouver des courbes elliptiques d'ordre supérieur est un défi pour les mathématiciens", a déclaré Park. Ou, peut-être, les mathématiciens "devraient reconsidérer leur opinion sur ce en quoi nous croyions, comme hypothèse populaire".