Les travaux d'Alexander Smith sur l'hypothèse de Goldfeld ont révélé les propriétés fondamentales des courbes elliptiques
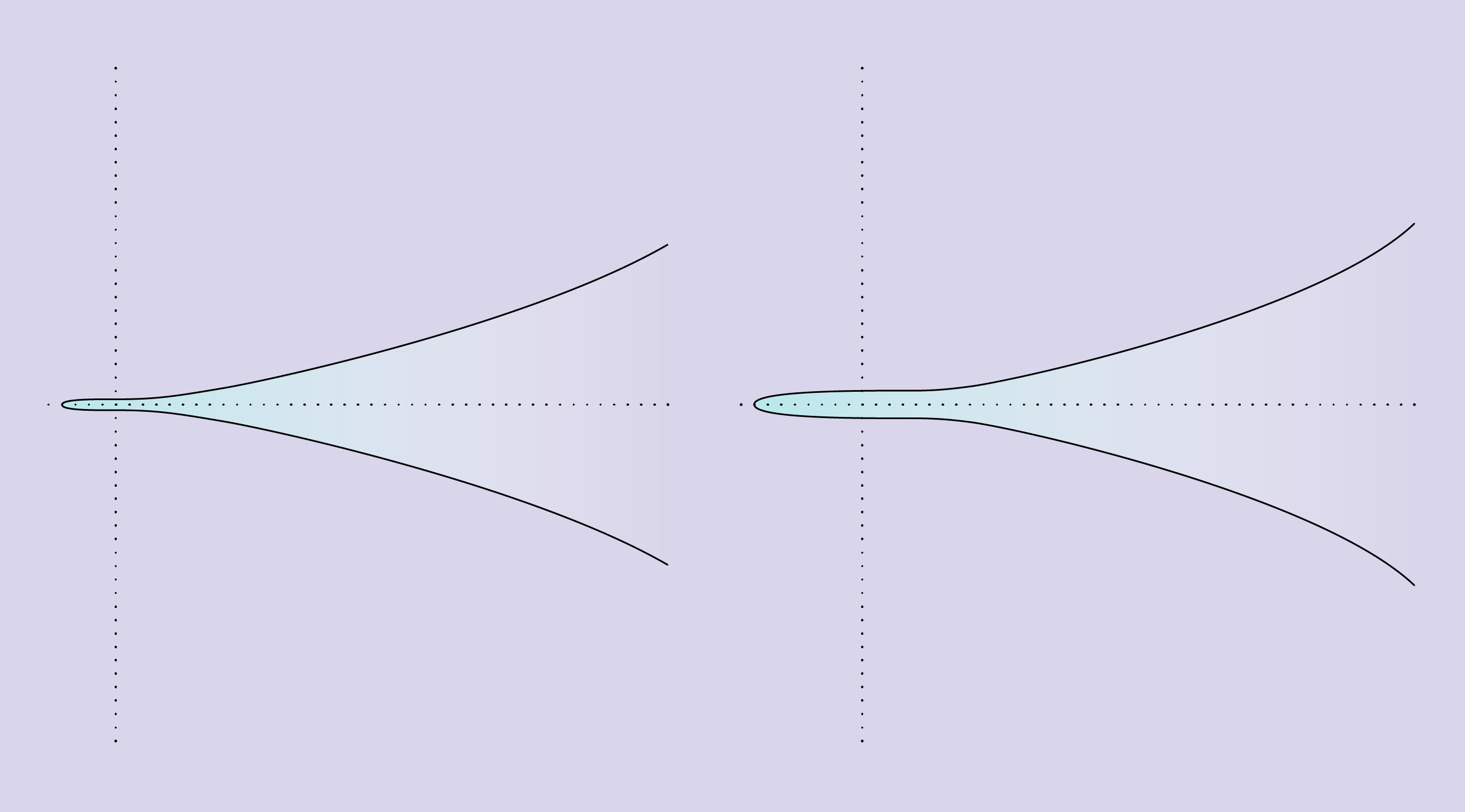Deux courbes elliptiques démontrent l'étrangeté du concept de rang. La courbe de gauche est décrite par l'équation y 2 = x 3 + 1, ne passe que par cinq points rationnels et a le rang 0. La courbe de droite est décrite par l'équation y 2 = x 3 + 8, passe par un nombre infini de points rationnels et a le rang 1.Il peut y avoir de nombreuses variantes de courbes elliptiques, mais il n'y a que deux de leurs variétés réelles. Ceci est le résultat des nouvelles preuves reçues par un étudiant diplômé de l'Université Harvard.
Les courbes elliptiques semblent exotiques, mais ce sont des objets géométriques banals, pas plus compliqués que les lignes droites, les paraboles ou les ellipses. Dans son
travail publié en ligne l'année dernière,
Alexadr Smith a prouvé l'hypothèse d'il y a quarante ans concernant la caractéristique fondamentale des courbes elliptiques de rang. Smith a prouvé que d'une famille donnée de courbes ayant une caractéristique, la moitié a un rang de 0 et l'autre moitié a un rang de 1.
Ce résultat établit une caractéristique de soutien des objets qui ont occupé les mathématiciens pendant de nombreux siècles, dont l'importance a surtout augmenté au cours des dernières décennies.
«Nous y réfléchissons depuis plus de 1000 ans, et nous avons maintenant une compréhension probabiliste des courbes elliptiques. C'est extrêmement important », a déclaré
Shaw-Wu Zhang , mathématicien à l'Université de Princeton qui a donné à Smith des recommandations sur son travail alors qu'il était encore étudiant à Princeton.
Les courbes elliptiques sont des équations avec des variables élevées à la troisième puissance, par exemple, y
2 = x
3 + 1. Elles sont apparues dans de nombreuses preuves mathématiques significatives au cours des dernières décennies, y compris la preuve la plus importante
du grand théorème de
Fermat de 1994. Une partie de leur signification réside dans le fait qu'ils appartiennent au type d'équations polynomiales le plus complexe, sur lequel les mathématiciens ont une sorte d'idées systémiques.
"Les courbes elliptiques sont un cas intéressant", a déclaré
Dorian Goldfeld , mathématicien à l'Université Columbia, qui a proposé en 1979 une hypothèse qui a obtenu son nom.
L'hypothèse de Goldfeld fait des prédictions sur le rang des courbes elliptiques. Comme nous l'avons déjà décrit dans un article récent, «
Quelles preuves les mathématiciens peuvent-ils convaincre s'il n'y a pas de preuve rigoureuse? » Le rang est une mesure de la complexité d'un ensemble de solutions rationnelles d'une courbe (solutions qui peuvent être représentées sous forme de fractions). Et bien qu'il n'y ait aucune restriction prouvée sur le rang de la courbe - jusqu'ici le 28 le plus élevé est considéré comme le rang le plus élevé - l'hypothèse de Goldfeld prédit qu'en moyenne la moitié des courbes elliptiques ont un rang de 0, et l'autre moitié en a 1.
Il peut ne pas vous sembler clair comment des courbes elliptiques avec un rang supérieur à 1 peuvent exister si la moitié des courbes elliptiques ont un rang 0 et l'autre moitié a 1. Si vous avez une boîte de balles de ping-pong, et si vous savez que exactement la moitié de ils sont noirs et la moitié sont blancs, alors il ne peut pas y en avoir de rouges.
Encore plus déroutant est le fait que les courbes elliptiques avec un rang de 2 ou plus existent non seulement quelques-unes, mais un nombre infini. Le résultat apparemment absurde est le résultat de statistiques astucieuses travaillant à l'infini. Même s'il y a beaucoup de courbes de rang 2 et plus, il y a tellement de courbes de rangs 0 et 1 que les courbes de rang 2 et plus ne sont pas statistiquement significatives. Si vous mettez toutes les courbes dans une boîte et que vous les en retirez au hasard, les chances de tirer une courbe avec un rang supérieur à 1 sont officiellement égales à zéro.
Qu'est-ce que cela signifie que le rang de la courbe est 0? De telles courbes ont un nombre fini de points rationnels - et pas plus de 16, comme
Barry Mazur l'a prouvé dans les années 1970.
Dorian GoldfeldIl y a des raisons de croire qu'un très grand nombre de courbes elliptiques auront un rang de 0. Si vous imaginez comment une courbe parcourt un plan, on verra que la plupart des points par lesquels elle passe ne seront pas rationnels. Ces points ne peuvent pas être exprimés en fractions, même s'ils sont arbitrairement complexes. Les chances qu'une courbe aléatoire croise de nombreux points rationnels - un ensemble infini - sont faibles.
"Je le prends de cette façon: si vous prenez une courbe elliptique aléatoire, alors il aura des raisons d'avoir un rang de 0. Il ne veut pas avoir de points rationnels", a déclaré Smith.
La prévalence des courbes de rang 1 est expliquée de manière similaire. Les courbes de rang 1 ont une infinité de points rationnels, mais tous sont parfaitement alignés, de sorte que vous pouvez les connecter les uns aux autres dans un processus assez simple.
Pour les courbes de rang 2 et plus, les ensembles de points rationnels sont plus compliqués. Ils contiennent plusieurs sous-ensembles infinis de points rationnels qui ne sont pas connectés les uns aux autres.
«Quelles sont les chances d'apparition de deux points indépendants? - dit Goldfeld. "Très faible." Mon hypothèse dit que cela devrait arriver rarement. »
Lorsque Goldfeld a présenté pour la première fois son hypothèse, la plupart des mathématiciens l'ont jugée incorrecte. Ils ont souligné les résultats d'expériences de calcul, dont il s'ensuit que les courbes de rang 2 ou plus se produisent beaucoup plus souvent que dans 0% des cas.
Goldfeld a répondu qu'ils prenaient simplement la gamme trop petite. Il a souligné que si vous étudiez uniquement les 10 premiers nombres entiers, vous pouvez obtenir une estimation extrêmement inexacte que 40% des nombres sont premiers. De même, ces expériences de calcul ont extrapolé de petits sous-ensembles de courbes elliptiques à des familles de courbes infiniment grandes.
«J'ai dit regardez les nombres premiers! C'était ma réponse. Nous devons monter beaucoup plus haut, car au début, beaucoup de plaisir peut apparaître », a déclaré Goldfeld.
L'hypothèse de Goldfeld ne s'applique pas à toutes les courbes elliptiques. Il décrit une famille spéciale de courbes elliptiques, de torsions quadratiques. Exemple: courbe elliptique cy
2 = x
3 - x, où c est une constante. En modifiant la valeur de c, vous courbez une courbe elliptique. L'hypothèse de Goldfeld se réfère à toute la variété infinie de courbes qui peuvent être obtenues en changeant la valeur de c.
Alexander Smith a témoigné que Goldfeld avait raison. Dans un nouvel article, il prouve que 100% des courbes elliptiques (d'un type spécial) ont un rang de 0 ou 1. Il a également prouvé que ces courbes sont également réparties entre les deux rangs, bien qu'il y ait un hic. Sa preuve de la division 50–50 est basée sur la validité
de l'hypothèse Birch - Swinnerton-Dyer (BJD). L'hypothèse BSD est l'un des problèmes ouverts les plus connus en mathématiques. Les mathématiciens ne sont pas encore proches de sa preuve, mais dans l'ensemble ils la considèrent comme vraie.
Même avec cette mise en garde, le résultat de Smith est considéré comme significatif. Les mathématiciens disent qu'il montre un moyen de prouver pleinement l'hypothèse de Goldfeld sans bricoler l'hypothèse décourageante de BSD. Cette méthode donne une nouvelle compréhension de la nature des courbes elliptiques.
"Le travail d'Alex Smith est extrêmement intéressant, et je pense qu'il doit encore être étudié et vu ce qu'il mérite", a déclaré
Melanie Wood , mathématicienne à l'Université du Wisconsin. «Le fait que cela puisse être prouvé est très important et révolutionnaire.»