Une implémentation pratique du générateur de commutation à l'aide de Verilog HDL

Résumé

Les registres à décalage à rétroaction linéaire sont un excellent outil pour implémenter un générateur de bits pseudo-aléatoires dans le matériel; ils inhibent une structure électronique simple et efficace. De plus, ils sont capables de produire des séquences de sortie avec de grandes périodes et de bonnes propriétés statistiques. Cependant, les LFSR standard ne sont pas sécurisés cryptographiquement, car la séquence de sortie peut être prédite de manière unique étant donné un petit nombre de bits de flux de clés en utilisant l'algorithme Berlekamp-Massey. Plusieurs méthodes ont été proposées pour détruire la linéarité inhérente à la conception LFSR. Ces méthodes comprennent des générateurs de combinaison non linéaires, des générateurs de filtres non linéaires et des générateurs contrôlés par horloge. Néanmoins, ils restent vulnérables à de nombreuses attaques telles que les attaques par canal latéral et les attaques algébriques. En 2015, un nouveau générateur commandé par horloge, appelé générateur à découpage, a été proposé. Ce nouveau générateur s'est avéré résistant aux attaques algébriques et aux attaques par canal latéral, tout en préservant les exigences d'efficacité et de sécurité. Dans ce projet, nous présentons une conception du générateur de commutation utilisant Verilog HDL.

Introduction et historique

L'histoire de la génération de nombres pseudo aléatoires dans le matériel est fortement liée au développement des chiffrements de flux. Les chiffrements de flux sont des chiffrements qui chiffrent les caractères de texte brut individuellement (généralement bit par bit), contrairement aux chiffrements par blocs, qui chiffrent le texte brut en gros blocs (64 bits ou plus). De nombreuses architectures de chiffrement de flux nécessitent un générateur de flux de clés, qui est un générateur de bits pseudo-aléatoires dont la graine est la clé de chiffrement. Pour chaque bit de texte brut, le bit de texte chiffré correspondant est calculé comme une fonction réversible (généralement une porte xor) du bit de texte brut et du bit de flux de clé correspondant. Par conséquent, la conception de générateurs de flux de clés sûrs et efficaces est essentielle pour le fonctionnement du chiffrement de flux.


Un outil utile pour construire des générateurs de flux clés est les registres à décalage à rétroaction linéaire. Ils peuvent être facilement transformés à l'aide de composants électroniques élémentaires et peuvent être programmés simplement sur des dispositifs logiques programmables. De plus, en raison de leur structure simple, les LFSR peuvent être modélisés et analysés mathématiquement, ce qui a conduit à un vaste ensemble de connaissances et de résultats les concernant. La séquence de sortie d'un LFSR correctement construit a une longueur exponentielle et de bonnes propriétés statistiques telles qu'une grande complexité linéaire.


Malgré les bonnes propriétés statistiques du LFSR, il ne peut pas être utilisé comme générateur de flux de clés sous sa forme standard en raison de sa nature linéaire. Si un attaquant a réussi à savoir $$$2L$ bits de flux de clés consécutifs, alors la séquence de sortie peut être prédite de manière unique et efficace en utilisant l'algorithme de Berlekamp-Massey, où $$$L$ est le nombre de registres. De nombreuses façons différentes de détruire la linéarité inhérente à la séquence de sortie LFSR ont été proposées:

• Utilisation de plusieurs LFSR et d'une fonction de combinaison non linéaire de leurs sorties (générateurs de combinaison non linéaire).
• Génération de la séquence de sortie en tant que fonction non linéaire de l'état LFSR (générateurs de filtres non linéaires).
• Synchronisation irrégulière des LFSR (générateurs commandés par horloge).

Pourtant, toutes ces conceptions sont restées vulnérables aux attaques telles que les attaques algébriques et latérales. Après l'an 2000, ce n'était plus un problème critique, car le chiffrement par blocs Rijndael a été proposé et élu comme Advanced Encryption Standard (AES). AES était capable de fonctionner en mode de chiffrement de flux et de répondre à toutes les normes industrielles pour un chiffrement de flux. De plus, avec l'augmentation des pouvoirs de calcul, AES pourrait être déployé sur diverses plates-formes. Cela a conduit à une diminution significative des applications de chiffrement de flux.


Adi Shamir a présenté une conférence invitée dans State of the Art dans Stream Ciphers 2004 et Asiacrypt 2004 intitulée "Stream Ciphers: Dead or Alive?". Dans sa présentation, il a suggéré que les chiffrements de flux peuvent survivre dans les applications suivantes:

• Applications orientées logiciel avec des vitesses exceptionnellement élevées (par exemple des routeurs).
• Applications orientées matériel avec un encombrement exceptionnellement faible (par exemple les cartes à puce).

L'une des dernières propositions de générateurs de flux clés est le générateur de commutation. Il est censé être résistant aux attaques algébriques et des canaux latéraux, tout en préservant l'efficacité et les vitesses de fonctionnement.


Dans ce projet, nous présenterons une conception du générateur de commutation en matériel, en utilisant Verilog HDL. Tout d'abord, nous présentons les deux formes courantes de LFSR, les LFSR de Fibonacci et les LFSR de Galois. Ensuite, nous présentons une présentation mathématique des LFSR. Nous présenterons ensuite le générateur de commutation tel qu'introduit par. Enfin, nous présentons notre conception Verilog du générateur de commutation.

Registres à décalage à rétroaction linéaire

Les registres à décalage à rétroaction linéaire sont des circuits constitués d'une liste linéaire de registres (également appelés éléments à retard) et d'un ensemble prédéfini de connexion entre eux. Un signal d'horloge global (unique) contrôle le flux de données à l'intérieur du LFSR. Les deux types de LFSR les plus couramment utilisés sont les LFSR de Fibonacci et les LFSR de Galois; ne différer que sous forme de connexions. Comme nous le verrons plus loin dans la section sur les modèles mathématiques, il existe de nombreuses similitudes entre les architectures de Fibonacci et de Galois, la préférence l'une par rapport à l'autre étant spécifique à l'application.


Tout au long de cet article, nous supposons un compteur de temps global hypothétique commençant à $$$0$ et augmentant de $$$1$ après chaque front positif du cycle d'horloge global.

Registres

Un registre est un élément logique capable de stocker un bit de données, appelé l'état. Il a deux lignes d'entrée: une ligne de données à un bit et une ligne de signal d'horloge. Il a une sortie d'un bit qui est toujours égale à l'état interne. À chaque front positif de l'entrée d'horloge, l'entrée de données est affectée à l'état, sinon l'état reste inchangé. Notons l'état d'un registre $$$S$ au moment $$$t$ comme $$$\ mathop S \ nolimits ^ t$ .

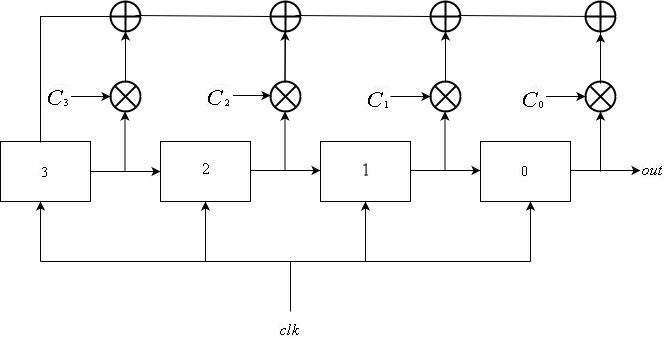
Fibonacci lfsrs

Un LFSR de Fibonacci se compose de $$$L$ registres énumérés à partir de $$$0$ à $$$L-1$ , tous connectés au même signal d'horloge. L'entrée du registre $$$i$ est la sortie du registre $$$i + 1$ pour $$$0 \ le i \ le L-2$ . L'entrée de rétroaction pour le registre $$$L-1$ est la somme xor des sorties d'un sous-ensemble de registres. La mise à jour du registre peut être décrite mathématiquement comme suit:

$$

$$\ mathop S \ nolimits_i ^ t = \ left \ {\ begin {array} {l} \ mathop S \ nolimits_ {i + 1} ^ {t-1} {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ rm {if} \ \} 0 \ le i \ le L-2 \\ \ mathop \ bigoplus \ limits_ {j = 1} ^ k \ mathop S \ nolimits_j ^ {t-1} \ otimes \ mathop C \ nolimits_j {\ \ \ \ \ rm {if} \ \} i = L-1 \ end {array} \ right.$$

où $$$C_j = 1$ si vous vous inscrivez $$$j$ est inclus dans les commentaires et $$$0$ sinon.

La séquence de sortie est obtenue à partir du registre $$$0$ . Autrement dit, la séquence de sortie est $$$\ mathop {\ left \ {{\ mathop S \ nolimits_0 ^ i} \ right \}} \ nolimits_ {i \ ge 0}$ .

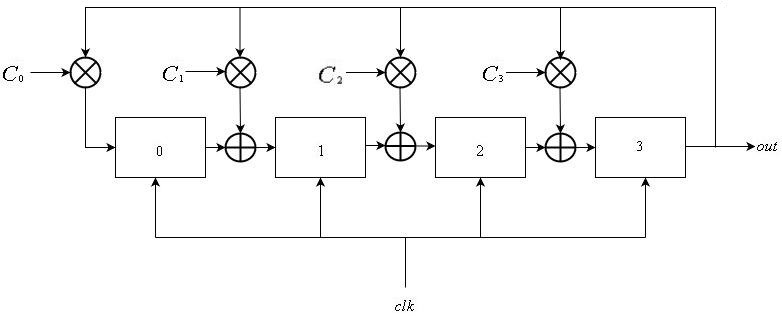
LFSR de Galois

Les LFSR de Galois consistent également en une liste linéaire de $$$L$ registres énumérés à partir de $$$0$ à $$$L-1$ , partageant tous le signal d'horloge global. L'entrée du registre $$$i$ est la sortie du registre $$$i-1$ pour $$$1 \ le i \ le L-1$ . Pour certains sous-ensembles de registres, leur entrée est xorée avec la sortie du registre $$$L-1$ . Cela peut s'exprimer comme suit:

$$

$$\ mathop S \ nolimits_i ^ t = \ left \ {\ begin {array} {l} \ mathop S \ nolimits_ {i-1} ^ {t-1} \ oplus \ mathop S \ nolimits_ {L-1} ^ {t-1} \ otimes \ mathop C \ nolimits_i {\ rm {\ \ \ \ if \ \}} 1 \ le i \ le L-1 \\ \ mathop S \ nolimits_ {L-1} ^ {t- 1} \ otimes \ mathop C \ nolimits_0 {\ rm {\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ if \ \}} i = 0 \ end {array} \ right.$$

où $$$C_i = 1$ si l'entrée du registre $$$i$ est xored avec la sortie du registre $$$L-1$ .


D'une manière similaire à celle des LFSR de Fibonacci, la séquence de sortie est définie comme $$$\ mathop {\ left \ {{\ mathop S \ nolimits_ {L-1} ^ i} \ right \}} \ nolimits_ {i \ ge 0}$ .

Comparaison entre Fibonacci et Galois Designs

Il existe une correspondance directe entre les LFSR de Fibonacci et de Galois au sens mathématique, comme nous le verrons dans la section suivante. Cependant, l'utilisation de la conception de Galois présente deux avantages notables:

• Dans la mise en œuvre logicielle, il ne nécessite pas de $$$L$ vérification de la parité des bits, qui ajoute un facteur logarithmique de complexité.
• Dans l'implémentation matérielle, il ne nécessite que des portes xor à deux entrées, dont le retard de propagation est nettement inférieur à celui des portes xor à entrées multiples utilisées dans la conception de Fibonacci.

Dans notre projet, nous considérons la formulation matricielle du LFSR, donc les deux architectures sont interchangeables.

Modèle mathématique des LFSR

Dans les sections suivantes, sauf indication contraire, nous supposons que tous les calculs sont effectués sous champ de Galois $$$Gf \ gauche (2 \ droite)$ . Autrement dit, toutes les opérations sont calculées modulo $$$2$ . Une autre implémentation de cette convention est que toute multiplication est une porte logique et que toute sommation est une porte xor.


Considérez les états de tous $$$L$ registres d'un LFSR à un moment donné $$$t$ ; cela peut être représenté comme un vecteur de $$${\ left \ {{0,1} \ right \} ^ L}$ :

$$

$${S ^ t} = \ left ({\ mathop S \ nolimits_0 ^ t; \ mathop S \ nolimits_1 ^ t; \ ldots; \ mathop S \ nolimits_ {L-1} ^ t} \ right)$$

Nous désignons ce vecteur comme l'état du LFSR. Notez qu'il y a tout au plus $$${2 ^ L}$ états possibles pour un $$$L$ enregistrer LFSR. Notez également que si un LFSR devait atteindre l'état zéro, il ne pourrait atteindre aucun autre état. Par conséquent, nous disons qu'il y a $$ non trivial d'un LFSR.


Considérez la transformation linéaire suivante:

$$

$$F = \ left ({\ begin {array} {* {20} {c}} 0 & 1 & \ cdots & 0 \\ \ vdots & \ vdots & \ ddots & \ vdots \\ 0 & 0 & \ cdots & 1 \\ {\ mathop C \ nolimits_0} & {\ mathop C \ nolimits_1} & \ cdots & {\ mathop C \ nolimits_ {L-1}} \ end {array}} \ right)$$

Étant donné que $$$\ mathop S \ nolimits ^ t$ est l'état d'un LFSR de Fibonacci, on peut observer que

$$

$$F \ cdot \ mathop S \ nolimits ^ t = \ mathop S \ nolimits ^ {t + 1}$$

Si $$$\ mathop S \ nolimits ^ t$ était un état d'un LFSR de Galois, alors considérons la transformation $$$G$ :

$$

$$G = \ left ({\ begin {array} {* {20} {c}} 0 & \ cdots & 0 & {\ mathop C \ nolimits_0} \\ 1 & \ cdots & 0 & {\ mathop C \ nolimits_1} \\ \ vdots & \ ddots & \ vdots & \ vdots \\ 0 & \ cdots & 1 & {\ mathop C \ nolimits_ {L-1}} \ end {array}} \ right)$$

Dans ce cas, nous avons

$$

$$G \ cdot \ mathop S \ nolimits ^ t = \ mathop S \ nolimits ^ {t + 1}$$

Les représentations matricielles des LFSR peuvent être flexibles lorsqu'il s'agit de mises à jour répétées, car elles peuvent être interprétées comme un simple produit matriciel. On constate que $$$F = {G ^ T}$ . Ce fait indique les nombreuses similitudes entre les plans de Fibonacci et de Galois s'ils étaient considérés comme des transformations linéaires $$${\ left \ {{0,1} \ right \} ^ N}$ à $$${\ left \ {{0,1} \ right \} ^ N}$ .


La multiplication du vecteur d'état de certains LFSR par une matrice (de type Fiboancci ou Galois) est connue sous le nom d'horloge ou de mise à jour du LFSR.

Le générateur de commutation

Le générateur de commutation est un générateur commandé par horloge proposé en 2015. Il est prouvé qu'il résiste aux attaques algébriques et à canaux latéraux. Dans cette section, nous présenterons la conception du générateur de commutation, telle que spécifiée par ses inventeurs.

Structure de base

Le générateur de commutation se compose de deux LFSR: un LFSR de commande $$$A$ de longueur $$$N$ et un LFSR de données $$$B$ de longueur $$$M$ . Le contrôle LFSR est mis à jour comme décrit précédemment. Cependant, le LFSR de données est mis à jour à l'aide de l'une des deux matrices possibles, $$$\ mathop M \ nolimits_1 ^ i$ ou $$$\ mathop M \ nolimits_2 ^ j$ , où $$${M_1}, {M_2}$ sont des matrices compagnes de certains polynômes primitifs. Le choix d'une matrice par rapport à l'autre est déterminé par la sortie du signal du LFSR de commande. Ce processus peut être décrit comme suit:

$$

$$\ mathop B \ nolimits ^ t = \ left \ {\ begin {array} {l} \ mathop M \ nolimits_1 ^ i \ cdot \ mathop B \ nolimits ^ {t-1} {\ rm {\ \ \ \ if \ \}} \ mathop A \ nolimits_ {M-1} ^ t = 0 \\ \ mathop M \ nolimits_2 ^ j \ cdot \ mathop B \ nolimits ^ {t-1} {\ rm {\ \ \ \ if \ \}} \ mathop A \ nolimits_ {M-1} ^ t = 1 \ end {array} \ right.$$

La sortie du générateur de commutation est la sortie de LFSR $$$B$ . Notez que nous avons supposé que $$$A$ est un LFSR de Galois. Il peut tout aussi bien s'agir d'un LFSR de Fibonacci.


Entiers $$$i, j$ Sont appelés les indices de commutation.

La graine

Rappelons qu'un LFSR peut parcourir au plus $$${2 ^ L} -1$ états non triviaux avant de revenir sur les états précédents. Depuis les matrices $$${M_1}, {M_2}$ sont des matrices de transformation de LFSR, on peut en déduire que les entiers $$$i, j$ peut être au maximum $$ avant que les matrices commencent à se répéter.


Le germe du générateur de commutation est $$$N + 3M$ bits, représentant les états initiaux des LFSR $$$A$ et $$$B$ et les puissances entières $$$i, j$ . Notez que les matrices $$${M_1}, {M_2}$ sont fixés tout au long de la mise en œuvre et ne sont pas inclus dans la graine.

Conception Verilog

Dans cette section, nous présenterons notre conception du générateur de commutation utilisant Verilog HDL. Nous présenterons chaque conception de module de façon ascendante. À la toute fin, nous présentons le module générateur de commutation.


Dans notre conception, nous avons essayé de réduire au minimum les composants synchrones. Les seuls composants contrôlés par horloge sont les LFSR $$$A, B$ .


Les opérations matricielles et vectorielles peuvent être mises en œuvre dans un certain nombre de méthodes différentes, variant en termes de consommation d'unités logiques, d'unités de mémoire et de complexité procédurale. Dans notre conception, nous éliminons le besoin de blocs procéduraux et utilisons les éléments logiques au maximum.


Toutes les matrices des modules suivants sont indexées à partir de $$$0$ de gauche à droite, puis de haut en bas.


Notez également que tous les modules ont des tailles paramétrées; c'est à des fins de débogage. Dans une implémentation réelle, toutes les tailles sont fixes.

Multiplexeur

Ceci est un module implémentant un 2 à 1 $$$N$ multiplexeur de bits. Le module a deux $$$N$ lignes d'entrée à 1 bit, une ligne de sélection à 1 bit et $$$N$ ligne de sortie -bit. Si l'entrée du sélecteur est $$$0$ alors la sortie est définie sur la première ligne d'entrée, sinon elle est définie sur la seconde.


Module multiplexeur

Transformation vectorielle

Ce module implémente une transformation linéaire sur un vecteur. Il accepte en entrée un $$$N \ fois N$ matrice de transformation et un $$$N$ -bit vecteur. Il produit le produit matrice-vecteur de son entrée.


Chaque bit du vecteur de sortie est le résultat d'un $$$N$ -bit xor gate, prenant en entrée le résultat de la $$$N$ -bit au niveau du bit et du vecteur d'entrée et de la ligne de matrice correspondante. Autrement dit, chaque bit de sortie est câblé à l'entrée et aucun bloc de procédure n'est nécessaire.


Exactement $$$N ^ 2$ deux entrées et portes sont utilisées, ainsi que $$$N$$$$N$ - portes xor d'entrée.


Module de transformation vectorielle

Identité

Ce module n'accepte aucune entrée. Son $$$N \ fois N$ la sortie -bit est initialisée à la $$$N$ matrice d'identité. Un tel module est déclaré par souci de commodité, de sorte que nous n'avons pas à initialiser un vecteur de registre global pour chaque taille différente.


Module de matrice d'identité

Transposer

Ce module accepte un $$$N \ fois N$ matrice et sortie sa transposition. Aucun élément logique ni élément mémoire n'est utilisé dans ce module, sa sortie n'est qu'une permutation de son entrée
.

Module de transposition matricielle

Multiplication de matrice

Il s'agit d'un module implémentant la multiplication matrice-matrice. Il accepte deux $$$N \ fois N$ matrices en entrée, et sort leur produit matrice-matrice.


Ce module contient une instance du module de transposition matricielle. Cela permet d'affecter des indices consécutifs aux colonnes de la deuxième matrice d'entrée. Chaque entrée de la matrice de sortie est ensuite affectée à la sortie d'un $$$N$ -entrée xor gate, dont l'entrée est au niveau du bit et de la ligne correspondante de la première matrice et de la colonne de la seconde.


Exactement $$$N ^ 3$ deux entrées et portes et $$$N ^ 2$$$$N$ Les xor d'entrée sont utilisés dans cette implémentation.


Module de multiplication de matrice

Exponentiation matricielle

Ce module élève une matrice à une puissance entière. Il accepte en entrée un $$$N \ fois N$ matrice et un $$$K$ -bit entier. Sa sortie est la matrice élevée à la puissance entière spécifiée.


Module d'exponentiation matricielle

Unité de contrôle

Ce module implémente le $$$N$ -bit control LFSR. Il s'agit de l'un des deux modules contrôlés par horloge de notre conception.


Il comprend un statique $$$N \ fois N$ Matrice de transformation LFSR et une variable $$$N$ état -bit. Son entrée comprend une horloge, un $$$N$ réinitialisation de l'état des bits et un signal de réinitialisation. Sa sortie est un seul bit, qui est le dernier bit du LFSR.


Après chaque front positif du signal d'horloge, l'état est mis à jour en fonction de la matrice de transformation à l'aide d'un module de multiplication matrice-vecteur. La réinitialisation d'état est affectée à l'état interne après chaque front positif du signal de réinitialisation.





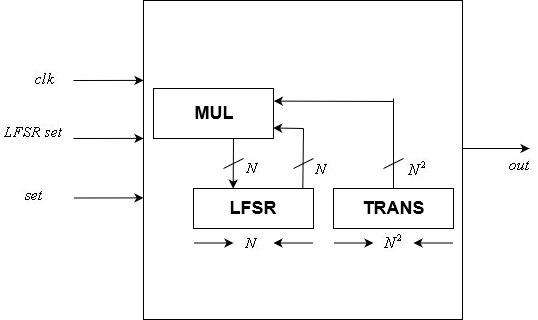Module d'unité de commande

Unité de données

Le $$$N$ LFSR de données est implémenté à l'aide de ce module. Comme le module de l'unité de contrôle, il est commandé par horloge


Le module comprend deux $$$N \ fois N$ matrices de transformation et un $$$N$ état LFSR -bit. Il accepte en entrée un signal d'horloge, un signal de commande, un $$$N$ réinitialisation de l'état LFSR à 2 bits, deux $$$N \ fois N$ la transformation de matrice est réinitialisée et un signal de réinitialisation. Il a une sortie d'un bit, le dernier bit du LFSR interne.


Notez que puisque la graine peut être modifiée, les matrices de transformation peuvent également être modifiées, contrairement à l'unité de contrôle dont la matrice de transformation est fixe.




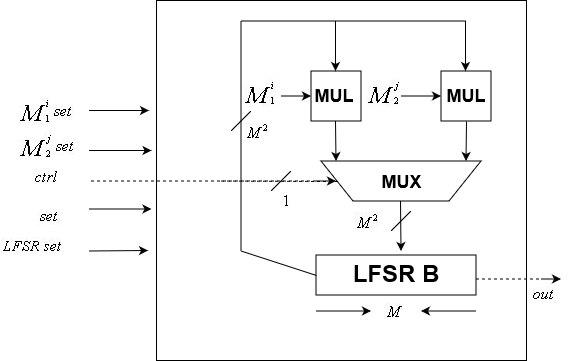\ Unité de données

Le générateur de commutation

Ceci est le module principal de notre conception. Il est paramétré par des entiers $$$N, M$ , qui sont les tailles des unités de contrôle et de données, respectivement.


L'entrée de ce module est un signal d'horloge, un $$$N + 3M$ -bit seed, et un signal défini. Le germe est simplement une concaténation de la réinitialisation du LFSR de contrôle, de la réinitialisation du LFSR de données et des nombres entiers $$$i, j$ Sa sortie est un bit, le bit pseudo aléatoire généré par le générateur de commutation.


Ce module comprend deux $$$M \ fois M$ matrices $$$\ mathop M \ nolimits_1, \ mathop M \ nolimits_2$ . Ces matrices sont fixées tout au long de l'implémentation.


Deux instances de modules d'exponentiation de matrice sont utilisées pour calculer les matrices d'entrée pour l'unité de données, où leurs entrées sont les matrices de transformation fixes et les entiers $$$i, j$ , extrait de la graine.


Le module générateur de commutation

Conclusions et recommandations

Dans ce projet, nous avons présenté une conception du générateur de commutation utilisant Verilog HDL. Cette conception est entièrement axée sur le matériel et élimine l'utilisation de blocs procéduraux. Une telle approche permet des performances maximales au détriment des éléments logiques et mémoire. Pour certaines applications avec des contraintes d'éléments logiques et de mémoire, il peut être avantageux de sacrifier les performances et d'augmenter l'utilisation de blocs procéduraux pour réduire l'utilisation des éléments électroniques.


Un inconvénient du projet est qu'il confie la responsabilité de choisir de bons indices de commutation à l'utilisateur. Un progrès possible consiste à ajouter un composant matériel pour vérifier la validité de l'index de commutation utilisé. Cela nécessite une implémentation matérielle d'algorithmes complexes tels que la recherche des caractéristiques polynomiales d'une matrice donnée et la vérification de la primitivité.


Un progrès possible consiste à ajouter un véritable générateur de nombres aléatoires pour vérifier les indices de commutation aléatoires et à sortir une paire valide une fois qu'il est trouvé. Il peut être prouvé que ce processus s'arrête après un court laps de temps avec une forte probabilité.

Les références

1. Katz, Jonathan et al. Manuel de cryptographie appliquée. Presse CRC, 1996.
2. Choi, Jun et al. "Le générateur de commutation: Nouveau générateur commandé par horloge avec une résistance contre les attaques algébriques et latérales." Entropie 17,6 (2015): 3692-3709.
3. Shamir, Adi. "Chiffres de flux: morts ou vivants?." ASIACRYPT. 2004.
4. LFSR pour les non-initiés