Les nouvelles preuves, rédigées par l'écrivain australien de science-fiction Greg Egan, et la preuve de 2011, publiée anonymement sur le net, ont été reconnues comme des percées importantes dans l'étude du mystère que les mathématiciens recherchent depuis 25 ans.

Le 16 septembre 2011, un fan d'anime a posté une question mathématique de 4chan sur la série culte "The
Melancholy of Haruhi Suzumiya " sur le forum. La première saison de l'émission, où il y avait des voyages dans le temps, a été diffusée dans un ordre différent de celui chronologique, et lors de l'émission et de la sortie ultérieures sur DVD, l'ordre des épisodes a de nouveau changé. Sur Internet, les fans ont discuté dans quel ordre il était préférable de regarder la série, et l'auteur de la question a demandé: si le public voulait voir la série dans tous les ordres possibles, combien d'épisodes figureraient sur leur liste la plus courte? [se
réfère à une liste dans laquelle vous pouvez trouver n'importe quelle séquence d'épisodes / env. perev. ]
En moins d'une heure, un auteur anonyme a
répondu à la question - pas une solution complète, mais une limite inférieure du nombre requis d'épisodes. De son raisonnement, applicable à n'importe quel nombre d'épisodes, il s'ensuit que pour la première saison de Haruhi, composée de 14 épisodes, le public devra regarder au moins 93884131311 épisodes d'affilée pour étudier toutes les permutations possibles. "Examinez les preuves des défauts que j'aurais pu manquer", a écrit l'auteur de la réponse.
Pendant sept ans, la preuve est passée inaperçue dans la communauté mathématique - il s'est avéré qu'à ce moment-là, seul un mathématicien professionnel l'a remarqué, et il ne l'a pas suffisamment étudié. Cependant, le mois dernier, l'écrivain australien de science-fiction
Greg Egan a prouvé une nouvelle
limite supérieure du nombre d'épisodes nécessaires. La découverte d'Egan a ravivé l'intérêt pour la tâche et a attiré l'attention sur le dossier concernant la limite inférieure de 2011. Ces deux preuves sont maintenant considérées comme des percées importantes dans l'étude du mystère que les mathématiciens étudient depuis au moins 25 ans.
Les mathématiciens ont rapidement vérifié la borne supérieure d'Egan, qui, comme la borne inférieure, est applicable aux séquences de n'importe quelle longueur. Ensuite, Robin Houston, mathématicien en visualisation de données à Kiln, et
Jay Panton de l'Université Marquette à Milwaukee ont confirmé indépendamment le travail d'un auteur anonyme avec 4chan. "Beaucoup d'efforts ont été consacrés à la vérification de la validité de cette hypothèse", a déclaré Panton, car les idées clés de la preuve n'étaient pas exprimées suffisamment clairement.
Et maintenant, Houston et Panton, avec
Vince Vater de l'Université de Floride, ont écrit un
ouvrage officiel . Dans ce document, ils ont indiqué le premier auteur comme «une affiche anonyme de 4chan».
"La chose étrange est que cette preuve très élégante d'un fait jusque-là inconnu est apparue dans un endroit aussi improbable", a déclaré Houston.
Villes de permutations
Si la série ne comporte que trois épisodes, il existe six façons de les regarder: 123, 132, 213, 231, 312 et 321. Ils peuvent être collés ensemble et faire une liste de 18 épisodes, y compris chaque version de la commande. Cependant, il existe également une méthode de collage plus efficace: 123121321. Une telle séquence contenant toutes les permutations d'un ensemble de n caractères est appelée super-permutation.
En 1993, Daniel Ashlock et Janet Tilotson ont découvert qu'en étudiant les super permutations les plus courtes pour diverses valeurs de n, les factorielles commencent rapidement à apparaître - les mêmes valeurs écrites sous la forme n!, C'est-à-dire en multipliant tous les nombres de 1 à n (par exemple, 4 ! = 4 * 3 * 2 * 1).
S'il n'y a qu'un seul épisode dans votre série, la durée de la super-permutation la plus courte sera de 1! (également connu sous le nom de la bonne vieille unité). Pour une série de deux épisodes, la super-permutation la plus courte (121) a une longueur de 2! + 1! .. Pour trois épisodes (exemple ci-dessus), la durée est de 3! + 2! + 1!, Et pour quatre épisodes (123412314231243121342132413214321) ce sera 4! + 3! + 2! + 1! .. La règle factorielle est devenue généralement acceptée (bien que personne ne puisse prouver qu'elle est vraie pour tout n), et les mathématiciens ultérieurs l'ont confirmée pour n = 5.
Puis en 2014, Houston a impressionné les mathématiciens,
montrant que pour n = 6, la règle a cessé de fonctionner. La règle prédit qu'il faudrait 873 épisodes pour regarder six épisodes de toutes les manières possibles, mais Houston a trouvé un moyen de le faire en 872. Et puisqu'il existe un moyen simple de transformer une super permutation courte pour n caractères en une super permutation courte pour n + 1 caractères, l'exemple de Houston signifie que la règle les factorielles ne fonctionnent pas pour tous n> 6.
La construction de Houston transforme la tâche de super-permutation en le célèbre problème des vendeurs ambulants, qui cherche le chemin le plus court à travers plusieurs villes. Plus précisément, les super permutations sont associées au problème du vendeur «asymétrique», dans lequel chaque trajet entre deux villes a son propre prix (pas nécessairement le même dans les deux sens), et l'objectif est de trouver le moyen le moins cher à travers toutes les villes.
Cette transformation est facile à comprendre: imaginez que chaque permutation est une ville, et imaginez le chemin de chaque permutation à chaque autre permutation. Dans le problème de la super-permutation, nous avons besoin de la séquence de chiffres la plus courte dans laquelle toutes les permutations sont présentes, notre objectif est donc de parcourir toutes les permutations afin d'ajouter le moins de nombres possible à la permutation initiale. Nous annonçons que le coût de chaque chemin est simplement le nombre de chiffres que nous devons attacher à la fin de la première permutation pour obtenir le second. Dans l'exemple avec n = 3, le chemin de 231 à 312 coûte 1 $, car nous devons ajouter seulement 2 à la fin de 231 pour obtenir 312, et le chemin de 231 à 132 coûte 2 $, car nous devons ajouter 32. Dans une telle formulation, le chemin le moins cher passe par toutes les villes correspondent directement à la super-permutation la plus courte.
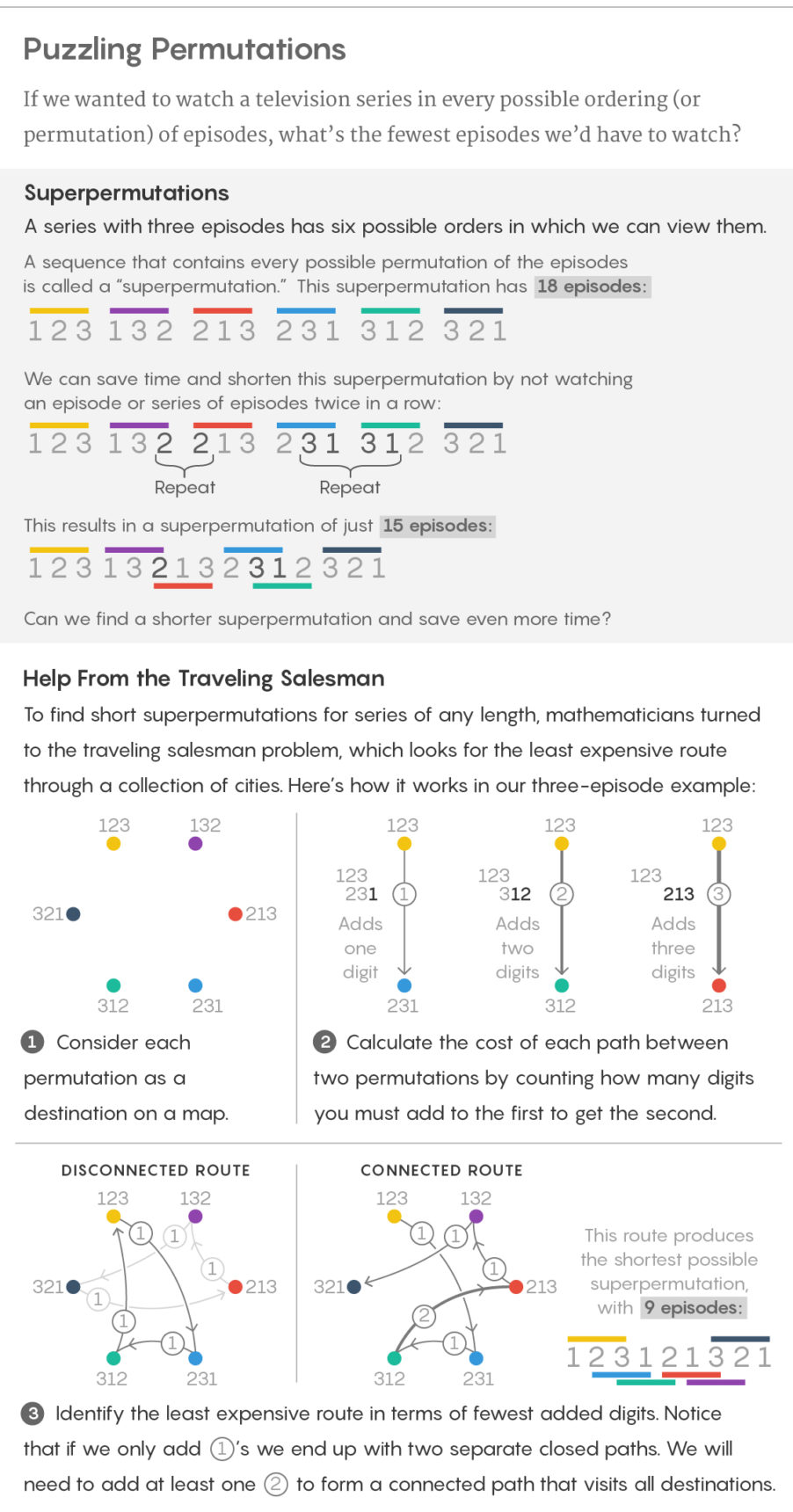
Une telle transformation signifiait que Houston pouvait diriger toutes les capacités des algorithmes pour résoudre le problème du voyageur de commerce vers le problème de la super-permutation. Ce problème est connu pour son appartenance à la classe des complexes NP, ce qui signifie l'absence d'un algorithme efficace pouvant le résoudre dans le cas général. Cependant, il existe des algorithmes qui peuvent résoudre efficacement certaines variétés du problème, et d'autres algorithmes peuvent produire de bonnes solutions approximatives. Houston a utilisé l'un de ces derniers pour émettre une super-permutation de 872 chiffres.
Puisqu'il n'a donné qu'une solution approximative, ce n'est peut-être même pas la super-permutation la plus idéale. Les mathématiciens effectuent actuellement une recherche informatique volumineuse pour la permutation à 6 caractères la plus courte, a déclaré Panton. "Nous savons que nos recherches se termineront dans un temps limité, mais nous ne savons pas si cela prendra une semaine ou un million d'années", a-t-il déclaré. "Il n'y a pas de barre de progression."
Mauvaise commande
Au moment où le travail de Houston est apparu, un poste anonyme sur 4chan était dans son coin Internet depuis près de trois ans. Un mathématicien,
Nathaniel Johnston de l'Université Mount Ellison, a remarqué une copie de ce message sur un autre site quelques jours après sa publication - et non pas parce qu'il était un amateur d'anime, mais parce qu'il a saisi diverses demandes dans Google, associée à des super-permutations.
Johnston a lu la preuve et elle lui a semblé fiable, mais il n'a pas perdu son énergie lors d'un examen approfondi. À cette époque, les mathématiciens pensaient que la formule factorielle pour les super-permutations était très probablement correcte, et lorsque vous pensez connaître la réponse exacte à une question, vous n'êtes pas intéressé par la limite inférieure de l'estimation. En d'autres termes, les épisodes de la série sur les super-permutations sont allés dans le mauvais ordre.
Après cela, Johnston a mentionné la limite inférieure sur une
paire de sites Web , mais "je ne pense pas que quiconque y ait prêté une attention particulière", a-t-il déclaré.
Puis, le 26 septembre 2018, le mathématicien
John Baez de l'Université de Californie à Riverside a tweeté un
article sur la découverte de Houston en 2014, dans le cadre d'une série de tweets sur des modèles mathématiques évidents qui ne fonctionnent plus.
Remarque perev.: il n'y avait pas une si grande série de tweets, seulement trois. Les deux autres sont également intéressants en eux-mêmes, bien qu'ils ne soient pas liés à cet article. On dit que 6 est la distance la plus populaire entre deux nombres premiers adjacents pour tous les nombres premiers inférieurs à 17 427 000 000 000 000 000 000 000 000 000 000. Et puis ce modèle cesse soudainement de fonctionner! La seconde montre la connexion suivante des intégrales, des fonctions trigonométriques et du nombre π

Mais seulement pour n <9,8 × 10 42 !Son tweet a attiré l'attention d'Egan, qui a étudié les mathématiques il y a plusieurs décennies, avant le début de sa carrière d'écrivain reconnu de science-fiction (sa première histoire à succès, par chance, s'appelait «La ville des permutations»). «Je n'ai jamais cessé de m'intéresser aux mathématiques», a écrit Egan dans l'e-mail.
Egan s'est demandé s'il était possible de créer une super-permutation encore plus courte que celle de Houston. Il s'est plongé dans l'étude de la littérature sur la façon de créer des raccourcis dans les réseaux de permutations, et après quelques semaines a trouvé ce dont il avait besoin. En quelques jours, il a déduit une nouvelle borne supérieure sur la longueur de la super-permutation la plus courte de n caractères: n! + (n - 1)! + (n - 2)! + (n - 3)! + n - 3. Elle est similaire à la formule factorielle, dont de nombreux membres ont été exclus.
"Il a complètement brisé la limite supérieure précédente", a déclaré Houston.
La borne inférieure de l'auteur de l'article sur 4chan était séduisante proche de la nouvelle borne supérieure: n! + (n - 1)! + (n - 2)! + n - 3. Après la publication du résultat, Egan Johnston a rappelé aux mathématiciens la preuve d'un auteur anonyme, et Houston et Panton ont rapidement prouvé son exactitude. Comme dans le travail de Houston, les nouvelles limites inférieures et supérieures sont adaptées aux super-permutations du point de vue du problème du voyageur de commerce: la limite inférieure montre que le chemin à travers toutes les villes doit passer par un nombre minimum de chemins valant plus de 1 $, et la limite supérieure crée un chemin spécial pour chaque n, en utilisant uniquement des composés d'une valeur de 1 $ et 2 $.
Maintenant, les chercheurs tentent de rapprocher les limites supérieure et inférieure et de trouver une formule unique qui résout le problème de la super-permutation. "Probablement, à la fin, les gens résoudront toujours cette énigme", a prédit Baez. "Maintenant, tout va bien."
Pour les fans de Haruhi, la solution d'Egan donne des instructions précises sur la façon de voir toutes les options possibles pour la première saison en utilisant un total de 93 924 230 411. Vous pouvez commencer à regarder aujourd'hui, ou vous pouvez attendre que les mathématiciens puissent réduire ce nombre. La borne inférieure d'un auteur anonyme prouve que cette réduction ne leur permettra pas de sauver plus de 40 millions d'épisodes - cependant, cela suffit pour commencer à préparer la deuxième saison.