Apprentissage de la latence: théorie de la file d'attente

Le thème de la latence dans le temps devient intéressant dans différents systèmes de Yandex et pas seulement. Cela se produit lorsque toute garantie de service apparaît dans ces systèmes. Évidemment, le fait est qu'il est important non seulement de promettre une opportunité aux utilisateurs, mais aussi de garantir sa réception avec un temps de réponse raisonnable. La «rationalité» du temps de réponse, bien sûr, varie considérablement selon les systèmes, mais les principes de base selon lesquels la latence se manifeste dans tous les systèmes sont communs et peuvent être considérés indépendamment des spécificités.

Je m'appelle Sergey Trifonov, je travaille dans l'équipe de Real-Time Map Reduce de Yandex. Nous développons une plate-forme pour le traitement des flux de données en temps réel avec des temps de réponse en seconde et sous-seconde. La plate-forme est disponible pour les utilisateurs internes et leur permet d'exécuter du code d'application sur des flux de données entrants en permanence. Je vais essayer de donner un bref aperçu des concepts de base de l'humanité sur le sujet de l'analyse de la latence au cours des cent dix dernières années, et maintenant nous allons essayer de comprendre ce qui peut être appris exactement sur la latence en utilisant la théorie des files d'attente.

Le phénomène de latence a commencé à être systématiquement étudié, à ma connaissance, dans le cadre de l'avènement des systèmes de files d'attente - les réseaux de communication téléphonique. La théorie de la file d'attente a commencé avec les travaux de A.K. Erlang en 1909, dans lesquels il a montré que la distribution de Poisson est applicable au trafic téléphonique aléatoire. Erlang a développé une théorie qui a été utilisée pendant des décennies pour concevoir des réseaux téléphoniques. La théorie nous permet de déterminer la probabilité d'un déni de service. Pour les réseaux téléphoniques avec des canaux à commutation de circuits, une défaillance s'est produite si tous les canaux sont occupés et que l'appel ne peut pas être effectué. La probabilité de cet événement devait être contrôlée. Je voulais avoir la garantie que, par exemple, 95% de tous les appels seraient traités. Les formules d'Erlang permettent de déterminer le nombre de serveurs nécessaires pour remplir cette garantie si la durée et le nombre d'appels sont connus. En fait, cette tâche ne concerne que les garanties de qualité, et aujourd'hui, les gens résolvent encore des problèmes similaires. Mais les systèmes sont devenus beaucoup plus complexes. Le principal problème de la théorie des files d'attente est qu'elle n'est pas enseignée dans la plupart des institutions, et peu de gens comprennent la question en dehors de la file d'attente M / M / 1 habituelle (voir la notation ci-dessous ), mais il est bien connu que la vie est beaucoup plus compliquée que ce système. Je vous propose donc, en contournant M / M / 1, de passer immédiatement au plus intéressant.

Valeurs moyennes

Si vous n'essayez pas d'acquérir une connaissance complète de la distribution de probabilité dans le système, mais que vous vous concentrez sur des questions plus simples, vous pouvez obtenir des résultats intéressants et utiles. Le plus célèbre d'entre eux est bien sûr le théorème de Little . Il est applicable à un système avec n'importe quel flux d'entrée, un périphérique interne de toute complexité et un ordonnanceur arbitraire à l'intérieur. La seule exigence est que le système doit être stable: des temps de réponse moyens et des longueurs de file d'attente doivent exister, puis ils sont connectés par une simple expression

$$

$$L = \ lambda W$$

où $$$L$ - le nombre moyen de demandes dans la partie considérée du système [pcs], $$$W$ - le temps moyen pendant lequel les demandes transitent par cette partie du ou des systèmes, $$$\ lambda$ - la vitesse de réception des demandes au système [pcs / s]. La force du théorème est qu'il peut être appliqué à n'importe quelle partie du système: file d'attente, exécuteur, file d'attente + exécuteur ou l'ensemble du réseau. Souvent, ce théorème est utilisé approximativement comme ceci: "Un flux de 1 Gbit / s se déverse vers nous, et nous avons mesuré le temps de réponse moyen, et il est de 10 ms, donc, en moyenne, nous avons 1,25 Mo en vol." Donc, ce calcul n'est pas vrai. Plus précisément, cela n'est vrai que si toutes les demandes ont la même taille en octets. Le théorème de Little compte les requêtes en morceaux, pas en octets.

Comment utiliser le théorème de Little

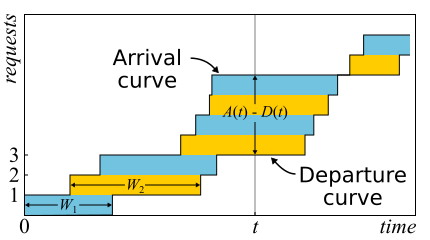
En mathématiques, il est souvent nécessaire d'étudier des données probantes pour avoir une réelle idée. C'est juste le cas. Le théorème de Little est si bon que je donne ici un croquis de la preuve. Le trafic entrant est décrit par la fonction $$$A (t)$ - le nombre de demandes connectées à l'époque $$$t$ . De même $$$D (t)$ - le nombre de demandes déconnectées à ce moment $$$t$ . Le moment d'entrée (sortie) de la demande est considéré comme le moment de réception (transmission) de son dernier octet. Les limites du système ne sont déterminées que par ces points dans le temps, par conséquent, le théorème est largement applicable. Si vous dessinez des graphiques de ces fonctions dans les mêmes axes, il est facile de voir que $$$A (t) - D (t)$ Est le nombre de demandes dans le système au temps t, et $$$W_n$ - temps de réponse de la nième requête.

Le théorème n'a été formellement prouvé qu'en 1961, bien que la relation elle-même était connue bien avant cela.

En fait, si les demandes peuvent être réorganisées dans le système, alors tout est un peu plus compliqué, donc pour simplifier, nous supposerons que cela ne se produit pas. Bien que le théorème soit également vrai dans ce cas. Calculons maintenant la zone entre les graphiques. Il y a deux façons de procéder. Tout d'abord, selon les colonnes - comme le pensent généralement les intégrales. Dans ce cas, il s'avère que l'intégrande est la taille de la file d'attente en morceaux. Deuxièmement, ligne par ligne - en ajoutant simplement la latence de toutes les demandes. Il est clair que les deux calculs donnent la même zone, ils sont donc égaux. Si les deux parties de cette égalité sont divisées par le temps Δt, pour lequel nous avons calculé l'aire, alors à gauche nous aurons la longueur moyenne de la file d'attente $$$L$ (par définition de la moyenne). À droite, c'est un peu plus délicat. Nous devons ajouter un autre nombre de requêtes N au numérateur et au dénominateur, puis nous réussirons

$$

$$\ frac {\ sum W_i} {\ Delta t} = \ frac {\ sum W_i} {N} \ frac {N} {\ Delta t} = W \ lambda$$

Si nous considérons suffisamment grand Δt ou une période d'emploi, les questions aux bords sont supprimées et le théorème peut être considéré comme prouvé.

Il est important de dire que dans la preuve, nous n'avons utilisé aucune distribution de probabilités. En fait, le théorème de Little est une loi déterministe! De telles lois sont appelées dans la théorie des files d'attente du droit opérationnel. Ils peuvent être appliqués à toutes les parties du système et à toutes les distributions de diverses variables aléatoires. Ces lois forment un constructeur qui peut être utilisé avec succès pour analyser les valeurs moyennes dans les réseaux. L'inconvénient est qu'ils s'appliquent tous uniquement aux moyennes et ne fournissent aucune connaissance sur les distributions.

Revenant à la question de savoir pourquoi le théorème de Little ne peut pas être appliqué aux octets, supposons que $$$A (t)$ et $$$D (t)$ maintenant, ils sont mesurés non pas en morceaux, mais en octets. Ensuite, en conduisant un argument similaire, nous obtenons à la place $$$W$ ce qui est étrange, c'est la surface divisée par le nombre total d'octets. C'est encore quelques secondes, mais c'est un peu une latence moyenne pondérée où les demandes plus importantes obtiennent plus de poids. Cette valeur peut être appelée la latence moyenne de l'octet - qui, en général, est logique, car nous avons remplacé les morceaux par des octets - mais pas la latence de la demande.

Le théorème de Little dit qu'avec un certain flux de demandes, le temps de réponse et le nombre de demandes dans le système sont proportionnels. Si toutes les demandes se ressemblent, le temps de réponse moyen ne peut pas être réduit sans augmenter la puissance. Si nous connaissons la taille des requêtes à l'avance, nous pouvons essayer de les réorganiser à l'intérieur pour réduire la zone entre $$$A (t)$ et $$$D (t)$ et donc le temps de réponse moyen du système. Poursuivant cette idée, nous pouvons prouver que les algorithmes de temps de traitement le plus court et de temps de traitement restant le plus court donnent un temps de réponse moyen minimum pour un serveur sans possibilité d'éviction, respectivement. Mais il y a un effet secondaire - les demandes importantes peuvent ne pas être traitées indéfiniment. Le phénomène est appelé «famine» et est étroitement lié au concept d'équité de la planification, qui peut être tiré d'un précédent article sur la planification: mythes et réalité .

Il existe un autre piège commun associé à la compréhension de la loi de Little. Il existe un serveur à thread unique qui répond aux demandes des utilisateurs. Supposons que nous mesurions en quelque sorte L - le nombre moyen de demandes dans la file d'attente pour ce serveur, et S - la durée moyenne pendant laquelle le serveur a traité une demande. Considérons maintenant une nouvelle demande entrante. En moyenne, il voit L requêtes devant lui. Servir chacun d'eux prend en moyenne S secondes. Il s'avère que le temps d'attente moyen $$$W = L S$ . Mais par le théorème, il s'avère que $$$W = L / \ lambda$ . Si nous égalisons les expressions, alors nous voyons le non-sens: $$$S = 1 / \ lambda$ . Quel est le problème avec ce raisonnement?

1. La première chose qui attire votre attention: le temps de réponse par le théorème ne dépend pas de S. En fait, bien sûr, il le fait. Seule la longueur moyenne de la file d'attente en tient déjà compte: plus le serveur est rapide, plus la longueur de la file d'attente est courte et plus le temps de réponse est court.
2. Nous considérons un système dans lequel les files d'attente ne s'accumulent pas indéfiniment, mais sont régulièrement réinitialisées. Cela signifie que l'utilisation du serveur est inférieure à 100% et nous ignorons toutes les demandes entrantes, et à la même vitesse moyenne avec laquelle ces demandes sont arrivées, ce qui signifie qu'en moyenne, il ne faut pas S secondes, mais plus, pour traiter une demande $$$1 / \ lambda$ secondes, simplement parce que parfois nous ne traitons aucune demande. Le fait est que dans tout système ouvert stable sans perte, le débit ne dépend pas de la vitesse des serveurs, il est déterminé uniquement par le flux d'entrée.
3. L'hypothèse qu'une demande entrante voit dans le système un nombre moyen de demandes dans le temps n'est pas toujours vraie. Contre-exemple: les demandes entrantes arrivent périodiquement et nous parvenons à traiter chaque demande avant l'arrivée de la suivante. Une image typique pour les systèmes en temps réel. Une demande entrante voit toujours zéro demande dans le système, mais en moyenne, le système a évidemment plus de zéro demande. Si les demandes arrivent à des moments complètement aléatoires, alors elles "voient vraiment le nombre moyen de demandes" .
   
   
   
4. Nous n'avons pas tenu compte du fait qu'avec une certaine probabilité, il peut déjà y avoir une demande dans le serveur qui doit être «étendue». Dans le cas général, la durée moyenne de «l'après-service» diffère de la durée initiale du service, et parfois, paradoxalement , elle peut s'avérer beaucoup plus longue. Nous reviendrons sur ce problème à la fin lorsque nous discuterons des microrafales, restez à l'écoute.

Ainsi, le théorème de Little peut être appliqué aux grands et petits systèmes, aux files d'attente, aux serveurs et aux threads de traitement uniques. Mais dans tous ces cas, les demandes sont généralement classées d'une manière ou d'une autre. Demandes d'utilisateurs différents, demandes de priorités différentes, demandes provenant de différents emplacements ou demandes de types différents. Dans ce cas, les informations agrégées par classes ne sont pas intéressantes. Oui, le nombre moyen de demandes mixtes et le temps de réponse moyen pour toutes sont à nouveau proportionnels. Mais que se passe-t-il si nous voulons connaître le temps de réponse moyen pour une certaine classe de demandes? Étonnamment, le théorème de Little peut être appliqué à une classe spécifique de requêtes. Dans ce cas, vous devez prendre $$$\ lambda$ Le taux auquel cette classe demande, pas tous. En tant que $$$L$ et $$$W$ - valeurs moyennes du nombre et du temps de séjour des demandes de cette classe dans la partie enquêtée du système.

Systèmes ouverts et fermés

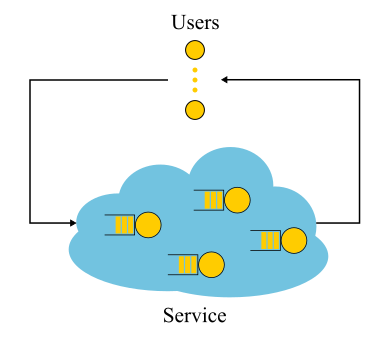
Il convient de noter que pour les systèmes fermés, le «mauvais» raisonnement menant à la conclusion $$$S = 1 / \ lambda$ se révèle être vrai. Les systèmes fermés sont les systèmes dans lesquels les demandes ne viennent pas de l'extérieur et ne vont pas à l'extérieur, mais circulent à l'intérieur. Ou, sinon, les systèmes de rétroaction: dès que la demande quitte le système, une nouvelle demande prend sa place. Ces systèmes sont également importants car tout système ouvert peut être considéré comme immergé dans un système fermé. Par exemple, vous pouvez considérer le site comme un système ouvert, dans lequel les demandes sont constamment versées, traitées et retirées, ou, au contraire, comme un système fermé avec l'ensemble de l'audience du site. Ensuite, ils disent généralement que le nombre d'utilisateurs est fixe, et ils attendent une réponse à la demande ou «réfléchissent»: ils ont reçu leur page et n'ont pas encore cliqué sur le lien. Dans le cas où le temps de réflexion est toujours nul, le système est également appelé système batch.

La loi de Little pour les systèmes fermés est valable si la vitesse des arrivées extérieures $$$\ lambda$ (ils ne sont pas dans un système fermé) remplacer par la bande passante du système. Si nous enveloppons le serveur monothread discuté ci-dessus dans un système batch, nous obtenons $$$S = 1 / \ lambda$ et 100% de recyclage. Souvent, un tel regard sur le système donne des résultats inattendus. Dans les années 90, c'est précisément cette vision de l'Internet avec les utilisateurs en tant que système unique qui a donné une impulsion à l'étude de distributions autres qu'exponentielles. Nous discuterons des distributions plus loin, mais ici, nous notons qu'à cette époque, presque tout et partout était considéré comme exponentiel, et cela a même été trouvé une justification, et pas seulement une excuse dans l'esprit de "sinon trop compliqué". Cependant, il s'est avéré que toutes les distributions pratiquement importantes n'ont pas la même queue, et la connaissance des queues de distribution peut être essayée. Mais pour l'instant, revenons aux valeurs moyennes.

Effets relativistes

Supposons que nous ayons un système ouvert: un réseau complexe ou un simple serveur à thread unique - cela n'a pas d'importance. Qu'est-ce qui changera si nous doublons l'arrivée des demandes et accélérons leur traitement de moitié - par exemple, en doublant la capacité de tous les composants du système? Comment l'utilisation, le débit, le nombre moyen de demandes dans le système et le temps de réponse moyen changeront-ils? Pour un serveur à thread unique, vous pouvez essayer de prendre les formules, les appliquer "sur le front" et obtenir les résultats, mais que faire avec un réseau arbitraire? La solution intuitive est la suivante. Supposons que le temps soit doublé, alors dans notre «référentiel accéléré» la vitesse des serveurs et le flux des requêtes ne semblent pas changer; en conséquence, tous les paramètres en temps accéléré ont les mêmes valeurs qu'auparavant. En d'autres termes, l'accélération de toutes les "pièces mobiles" de tout système équivaut à l'accélération de l'horloge. Nous allons maintenant convertir les valeurs en un système avec un temps normal. Les quantités sans dimension (utilisation et nombre moyen de demandes) ne changeront pas. Les valeurs dont la dimension comprend des facteurs temporels du premier degré varient proportionnellement. Le débit de [requêtes / s] sera doublé, et les temps de réponse et d'attente [s] seront divisés par deux.

Ce résultat peut être interprété de deux manières:

1. Un système accéléré par k fois peut digérer le flux de tâches k fois plus, et avec un temps de réponse moyen k fois moins.
2. On peut dire que la puissance n'a pas changé, mais simplement que la taille des tâches a diminué k fois. Il s'avère que nous envoyons la même charge au système, mais sciée en plus petits morceaux. Et ... oh, un miracle! Le temps de réponse moyen est réduit!

Encore une fois, je note que cela est vrai pour une large classe de systèmes, et pas seulement pour un simple serveur. D'un point de vue pratique, il n'y a que deux problèmes:

1. Toutes les parties du système ne peuvent pas être facilement accélérées. Nous ne pouvons pas en influencer du tout. Par exemple, la vitesse de la lumière.
2. Toutes les tâches ne peuvent pas être divisées à l'infini en plus petites et plus petites, car aucune information n'a été apprise pour être transférée par portions de moins d'un bit.

Considérez le passage à la limite. Supposons, dans le même système ouvert, l'interprétation n ° 2. Nous divisons chaque demande entrante en deux. Le temps de réponse est également divisé par deux. Répétez la division plusieurs fois. Et nous n'avons même pas besoin de changer quoi que ce soit dans le système. Il s'avère que vous pouvez réduire arbitrairement le temps de réponse en sciant simplement les demandes entrantes en un nombre suffisamment important de pièces. À la limite, nous pouvons dire qu'au lieu de requêtes, nous obtenons un «fluide de requête», que nous filtrons par nos serveurs. Il s'agit du modèle dit fluide, un outil très pratique pour une analyse simplifiée. Mais pourquoi le temps de réponse est-il nul? Qu'est-ce qui a mal tourné? Où n'avons-nous pas considéré la latence? Il s'avère que nous n'avons pas pris en compte uniquement la vitesse de la lumière, elle ne peut pas être doublée. Le temps de propagation dans le canal réseau ne peut pas être modifié, vous ne pouvez que le supporter. En fait, la transmission sur un réseau comprend deux composantes: le temps de transmission et le temps de propagation. Le premier peut être accéléré en augmentant la puissance (largeur du canal) ou en réduisant la taille des paquets, et le second est très difficile à influencer. Dans notre «modèle liquide», il n'y avait tout simplement pas de réservoirs pour l'accumulation de liquides - des canaux de réseau avec des temps de propagation non nuls et constants. Soit dit en passant, si nous les ajoutons à notre «modèle liquide», la latence sera déterminée par la somme des temps de propagation, et les files d'attente dans les nœuds seront toujours vides. Les files d'attente dépendent uniquement de la taille des paquets et de la variabilité (lecture en rafale) du flux d'entrée.

Il s'ensuit qu'en matière de latence, vous ne pouvez pas vous débrouiller avec le calcul des flux, et même le recyclage des appareils ne résout pas tout. Il est nécessaire de prendre en compte la taille des demandes et de ne pas oublier le temps de distribution, qui est souvent ignoré dans la théorie des files d'attente, bien que l'ajouter aux calculs ne soit pas du tout difficile.

Distributions

Quelle est la raison de la mise en file d'attente? De toute évidence, le système n'a pas assez de capacité, et l'excès de demandes s'accumule? Pas vrai! Des files d'attente surviennent également dans les systèmes où les ressources sont suffisantes. S'il n'y a pas assez de capacité, alors le système, comme disent les théoriciens, n'est pas stable. Il y a deux raisons principales à la mise en file d'attente: l'irrégularité des demandes et la variabilité de la taille des demandes. Nous avons déjà examiné un exemple dans lequel ces deux raisons ont été éliminées: un système en temps réel où les demandes de même taille arrivent strictement périodiquement. Une file d'attente ne se forme jamais. Le temps d'attente moyen dans la file d'attente est nul. , , , . , .

A/S/k/K, A — , S — , k — , K — (, ). , M/M/1 : M (Markovian Memoryless) , . : $$$\lambda$ — — , : . M , μ . , , . , 4- . , , : G — (, , ), D — deterministic. C — D/D/1. , 1909 ., — M/D/1. — M/G/k k>1, M/G/1 1930-.

?

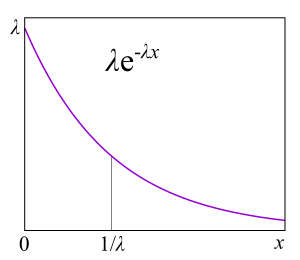
, , , , , . , . , failure rate . , , : , . failure rate function, . , «» , . , : , . , failure rate — , , - , — . , , , , , . « ».

Failure rate . — . Failure rate , , , . failure rate, , , . failure rate, , , . , , , software hardware? : ? . , , - . ? , — . ( failure rate) . « » .

, , failure rate, , , unix- . , .

RTMR , . LWTrace - . . , . , $$$\mathbf{P}\{S>x\}$ . , failure rate , , : .



$$$\mathbf{P}\{S>x\} = x^{-a}$ , — . , « », 80/20: , . . , . , RTMR -, , . Paramètre $$$a=1.16$ , 80/20: 20% 80% .

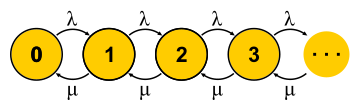
, . . , , , - . , — . « » , « » — . : , ? , ( , ), . , 0 . , , $$$\mu N_1$ $$$\lambda N_0$ . , , — . . , . M/M/1 $$$\mathbf{P}\{Q=i\} = (1 - \rho) \rho^i$ où $$$\rho = \lambda / \mu$ - C'est l'utilisation du serveur. La fin de l'histoire. Au cours de la présentation, j'ai raté une quantité décente d'hypothèses et j'ai fait quelques substitutions de concepts, mais l'essence, je l'espère, n'a pas souffert.

Il est important de comprendre que cette approche ne fonctionne que si l'état actuel de la machine détermine pleinement son comportement ultérieur, et l'histoire de la façon dont elle est entrée dans cet état n'est pas importante. Pour la compréhension quotidienne d'une machine à états finis, cela va de soi - après tout, c'est une condition pour cela. Mais pour un processus stochastique, il en résulte que toutes les distributions doivent être exponentielles, car seules elles n'ont pas de mémoire - elles ont un taux d'échec constant.

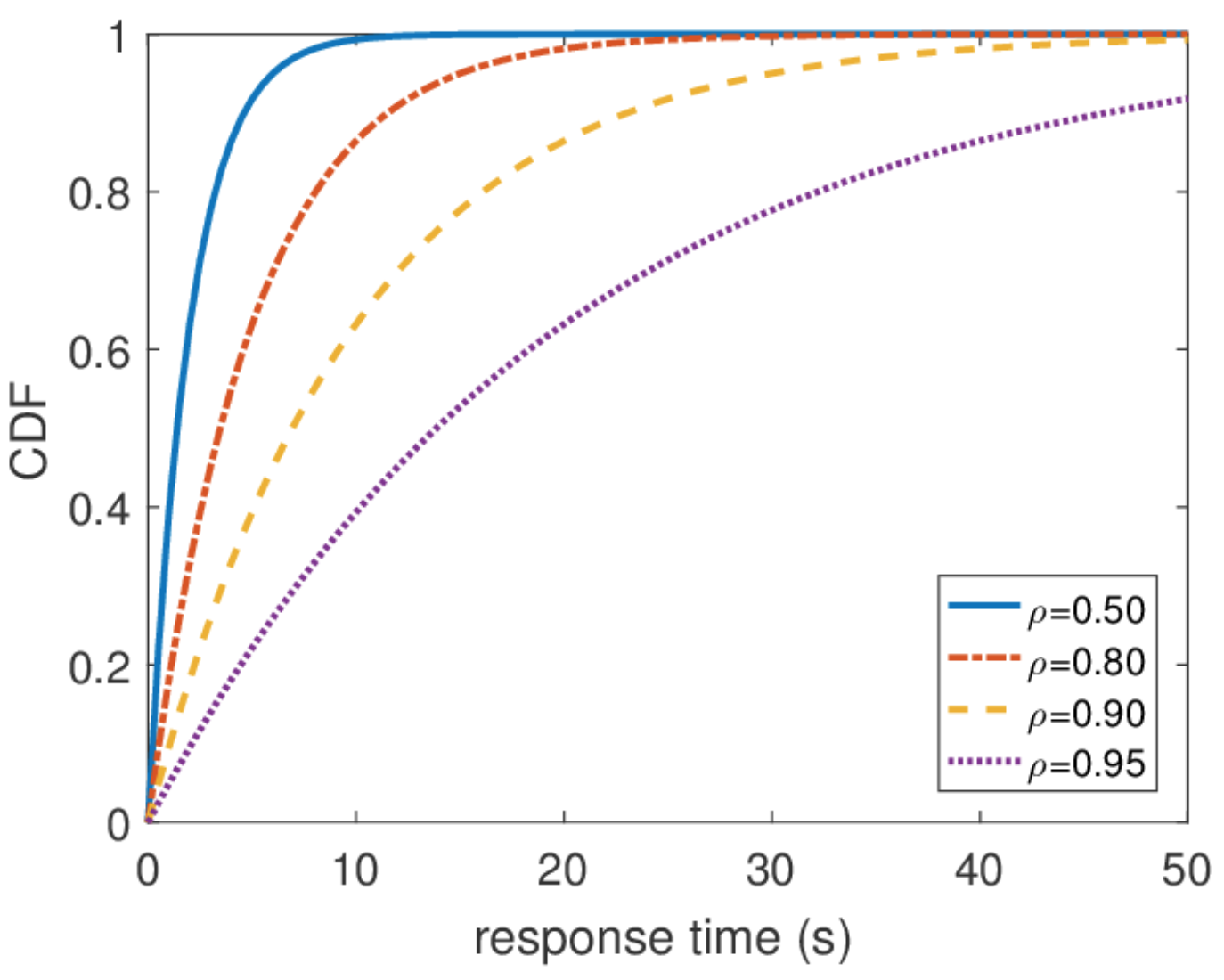
Il est également important de dire que toutes les autres informations sur le système sont faciles à obtenir si nous connaissons la distribution d'équilibre. Le nombre moyen de requêtes dans le système est la moyenne de cette distribution. Pour connaître le temps de réponse moyen, nous appliquons le théorème de Little au nombre de requêtes. La distribution du temps de réponse est un peu plus difficile à trouver, mais aussi en quelques actions vous pouvez découvrir que $$$\ mathbf {P} \ {response \ _time> t \} = e ^ {- (\ mu- \ lambda) t}$ et quel est le temps de réponse moyen $$$1 / (\ mu- \ lambda)$ .

Temps de réponse illimité

À partir de cette distribution, vous pouvez trouver n'importe quel centile du temps de réponse, et il s'avère que le centième centile est égal à l'infini. En d'autres termes, le pire temps de réponse n'est pas limité par le haut. Ce qui, en général, n'est pas surprenant, puisque nous avons utilisé le flux de Poisson. Mais en pratique, un tel comportement ne peut jamais être rencontré. De toute évidence, le flux d'entrée de requêtes vers le serveur est limité, au moins par la largeur du canal réseau vers ce serveur, et la longueur de la file d'attente est limitée par la mémoire sur ce serveur. Le flux de Poisson, au contraire, avec une probabilité non nulle garantit l'occurrence de salves arbitrairement grandes. Par conséquent, je ne recommanderais pas de partir de l'hypothèse d'un flux d'entrée de Poisson lors de la conception d'un système si vous êtes intéressé par des centiles élevés et que la charge du système est très élevée. Il vaut mieux utiliser d'autres modèles de trafic, dont je parlerai une autre fois lorsque je parlerai du calcul du réseau.

Mise à l'échelle et garanties

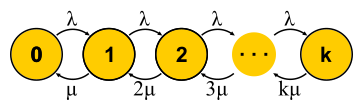
Maintenant que nous avons un moyen suffisamment puissant pour analyser les systèmes, nous pouvons essayer de l'appliquer à différentes tâches et en récolter les fruits. C'est ainsi que la théorie du service de masse s'est développée dans la seconde moitié du 20e siècle. Essayons de comprendre ce qui a été réalisé. Pour commencer, revenons aux tâches qu'Erlang a résolues. Ce sont les tâches M / M / k / k et M / M / k, dans lesquelles nous voudrions limiter la probabilité d'échec. Il s'avère qu'il n'est pas difficile pour eux de construire des chaînes de Markov. La différence est que lorsque des tâches sont ajoutées, la probabilité d'une transition inverse augmente, car les tâches commencent à être traitées en parallèle, mais lorsque le nombre de tâches devient égal au nombre de serveurs, la saturation se produit. De plus, pour M / M / k / k, le réseau se termine, l'automate se révèle vraiment fini et toutes les requêtes qui arrivent au dernier état sont refusées. La probabilité de cet événement est simplement égale à la probabilité que nous soyons dans le dernier état.

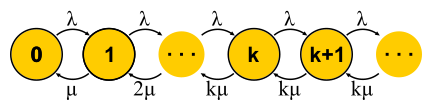
Pour M / M / k, la situation est plus compliquée, les demandes sont mises en file d'attente, de nouveaux états apparaissent, mais la probabilité d'une transition inverse n'augmente pas - tous les serveurs fonctionnent déjà. Le réseau devient infini, comme pour M / M / 1. Soit dit en passant, si le nombre de demandes dans le système est limité, la chaîne aura toujours un nombre fini d'états et d'une manière ou d'une autre, elle sera résolue, ce qui ne peut pas être dit des chaînes sans fin. Dans les systèmes fermés, les chaînes sont toujours finies. En résolvant les circuits décrits pour M / M / k / k et M / M / k, nous arrivons à la formule B et à la formule d' Erlang C, respectivement. Ils sont plutôt volumineux, je ne les donnerai pas, mais avec leur aide, vous pouvez obtenir un résultat intéressant pour le développement de l'intuition, qui s'appelle la règle de dotation en racine carrée. Supposons qu'il existe un système M / M / k avec un flux d'entrée donné λ de requêtes par seconde. Supposons que la charge double d'ici demain. La question est: comment augmenter le nombre de serveurs pour que le temps de réponse reste le même? Le nombre de serveurs doit être doublé, non? Il s'avère que ce n'est pas du tout. Rappelons que nous l'avons déjà vu: si vous accélérez de moitié (serveurs et connexion), le temps de réponse moyen diminue de moitié. Plusieurs serveurs lents et un serveur rapide ne sont pas la même chose, mais néanmoins la puissance de calcul est la même. En particulier, pour M / M / 1, par exemple, le temps de réponse est inversement proportionnel au volume de «capacité libre» $$$\ mu - \ lambda$ et est déterminé uniquement par ce volume. En doublant à la fois le débit et la puissance de traitement, la capacité libre du système double: $$$2 \ mu - 2 \ lambda$ . Il peut sembler que pour résoudre le problème, il vous suffit d'économiser la capacité libre, mais le temps de réponse en M / M / k est déjà déterminé par la formule Erlang plus complexe. Il s'avère que la capacité libre doit être maintenue proportionnellement à la racine carrée du nombre de «serveurs occupés» afin de maintenir le même temps de réponse. Par le nombre de «serveurs occupés», on entend le nombre total de serveurs multiplié par l'utilisation: c'est le nombre minimum de serveurs nécessaires à un fonctionnement stable.

En utilisant cette règle, ils essaient parfois de justifier la façon d'étendre un cluster avec des serveurs. Mais ne vous faites pas l'illusion qu'un cluster est un système M / M / k. Par exemple, si vous avez un équilibreur à votre entrée qui envoie des demandes dans des files d'attente aux serveurs, ce n'est plus M / M / k, car M / M / k implique une file d'attente commune à partir de laquelle les serveurs récupèrent les demandes lorsqu'elles sont libérées. Mais ce modèle convient, par exemple, aux pools de threads avec une file d'attente FIFO commune. Cependant, même dans ce cas, il convient de rappeler que cette règle est une approximation pour le cas où il y a beaucoup de threads. En fait, si vous avez plus de 10 threads, vous pouvez supposer qu'il y en a beaucoup. Eh bien, n'oubliez pas les distributions exponentielles omniprésentes: sans supposer l'exponentialité de toutes les distributions, la règle ne fonctionne pas non plus.

Temps de réponse réseau

En fin de compte, l'intérêt est un réseau de M / M / k connecté au moins dans une chaîne, car nous faisons des systèmes distribués. Pour étudier les réseaux, j'aimerais avoir un constructeur: des règles simples et claires pour connecter des éléments connus en blocs. Dans la théorie du contrôle, par exemple, il existe des fonctions de transfert qui sont naturellement combinées avec des connexions série ou parallèles. Ici, le flux de sortie de n'importe quel nœud a une distribution très compliquée, à l'exception de M / M / k, qui, selon le théorème de Burke bien connu , produit un flux de Poisson indépendant. Cette exception, comme vous pouvez le deviner, est principalement utilisée.

La connexion de deux flux de Poisson est un flux de Poisson. La séparation probabiliste du flux de Poisson en deux donne à nouveau deux flux de Poisson. Tout cela conduit au fait que toutes les files d'attente du système sont comme indépendantes, et vous pouvez obtenir, dans un langage formel, la solution dite de forme de produit . En d'autres termes, la distribution conjointe des longueurs des files d'attente est simplement le produit des distributions des longueurs de toutes les files d'attente, considérées séparément - c'est ainsi que l'indépendance est exprimée dans la théorie des probabilités. Nous trouvons simplement les flux d'entrée vers tous les nœuds et utilisons les formules pour chaque nœud indépendamment. Il existe un certain nombre de limitations:

1. Algorithme de routage probabiliste. La demande servie par le nœud sélectionne le suivant de façon aléatoire avec une probabilité connue. Ce n'est pas aussi mauvais que cela puisse paraître, car il est possible d'utiliser des "classes de demande": disons que toutes les demandes de Vasya arrivent au serveur n ° 1, puis au serveur n ° 2 puis sortent du réseau, et les demandes de Petya arrivent au serveur n ° 2 , puis avec une probabilité égale, visitez le serveur numéro 1 ou numéro 3 et quittez. Autrement dit, toutes les transitions ne doivent pas être aléatoires, certaines ou même toutes peuvent avoir une probabilité de 100%.
2. Assomption de l'indépendance de Kleinrock. Le temps de traitement de la demande ne peut pas dépendre de l'historique ou de la classe de la demande, mais est déterminé uniquement par le serveur, et lorsque la demande passe à nouveau sur le même serveur, elle est sélectionnée au hasard à chaque fois. En fait, il n'y a aucun moyen de définir la taille de la demande qui serait utilisée sur différents serveurs et la durée de service est déterminée uniquement par le serveur lui-même. Vous pouvez également essayer de contourner cette limitation. Pour cela, un routage probabiliste est généralement utilisé et une boucle est effectuée pour revenir au même serveur avec une certaine probabilité - comme s'ils redémarraient la demande. À mon avis, c'est une astuce plutôt étrange, car une telle demande rentre dans la file d'attente et n'est pas exécutée immédiatement, mais pour certaines tâches, ce n'est pas important.
3. Trafic d'entrée de Poisson et temps de service exponentiel sur tous les nœuds.

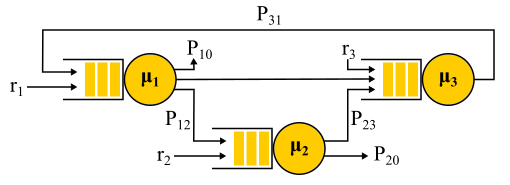
Exemple de réseau Jackson.

Il convient de noter qu'en présence de rétroaction, un flux de Poisson N'EST PAS obtenu, car les flux se révèlent interdépendants. À la sortie du nœud de rétroaction, un flux non-Poisson est également obtenu, et par conséquent, tous les flux deviennent non-Poisson. Cependant, de manière surprenante, il s'avère que tous ces flux non-Poisson se comportent exactement de la même manière que les flux de Poisson (oh, cette théorie des probabilités) si les restrictions ci-dessus sont satisfaites. Et là encore, nous obtenons une solution sous forme de produit. Ces réseaux sont appelés réseaux Jackson , ils peuvent fournir des commentaires et, par conséquent, des visites multiples à n'importe quel serveur. Il existe d'autres réseaux dans lesquels plus de libertés sont autorisées, mais en conséquence, toutes les réalisations analytiques importantes de la théorie des files d'attente par rapport aux réseaux impliquent des flux de Poisson à la solution d'entrée et de forme de produit, qui sont devenus l'objet de critiques de cette théorie et ont conduit dans les années 90 à le développement d'autres théories, et l'étude de ce qui est réellement nécessaire de distribution et comment travailler avec eux.

Une application importante de toute cette théorie des réseaux Jackson est la modélisation de paquets dans les réseaux IP et les réseaux ATM. Le modèle est tout à fait adéquat: les tailles de paquet ne varient pas beaucoup et ne dépendent pas du paquet lui-même, seulement de la largeur du canal, car le temps de service correspond à l'heure à laquelle le paquet a été envoyé au canal. Le temps d'envoi aléatoire, même s'il semble sauvage, n'a en fait pas de très grande variabilité. De plus, il s'avère que dans un réseau avec un temps de service déterministe, la latence ne peut pas être plus grande que dans un réseau Jackson similaire, de sorte que ces réseaux peuvent être utilisés en toute sécurité pour estimer le temps de réponse d'en haut.

Distributions non exponentielles

Tous les résultats dont j'ai parlé étaient liés aux distributions exponentielles, mais j'ai également mentionné que les distributions réelles sont différentes. On a le sentiment que toute cette théorie est tout à fait inutile. Ce n'est pas tout à fait vrai. Il existe un moyen d'intégrer d'autres distributions dans cet appareil mathématique, d'ailleurs, pratiquement toutes les distributions, mais cela nous coûtera quelque chose. À l'exception de quelques cas intéressants, l'opportunité d'obtenir une solution sous une forme explicite est perdue, la solution sous forme de produit est perdue, et avec elle le constructeur: chaque problème doit être résolu entièrement à partir de zéro en utilisant des chaînes de Markov. Pour la théorie, c'est un gros problème, mais en pratique, cela signifie simplement l'application de méthodes numériques et permet de résoudre des problèmes beaucoup plus complexes et proches de la réalité.

Méthode de phase

L'idée est simple. Les chaînes de Markov ne nous permettent pas d'avoir de la mémoire à l'intérieur d'un état, donc toutes les transitions doivent être aléatoires avec une distribution exponentielle du temps entre deux transitions. Mais que se passe-t-il si l'État est divisé en plusieurs sous-états? Les transitions entre sous-états doivent toujours avoir une distribution exponentielle si nous voulons que toute la structure reste une chaîne de Markov, et nous le voulons vraiment, car nous savons comment résoudre de telles chaînes. Les sous-états sont souvent appelés phases s'ils sont organisés en série, et le processus de partition est appelé la méthode des phases.

L'exemple le plus simple. La demande est traitée en plusieurs phases: d'abord, par exemple, nous lisons les données nécessaires dans la base de données, puis nous effectuons quelques calculs, puis nous écrivons les résultats dans la base de données. Supposons que ces trois étapes aient la même distribution exponentielle du temps. Quelle distribution a le temps de transit des trois phases ensemble? Ceci est la distribution d'Erlang.



Mais que se passe-t-il si vous réalisez de nombreuses phases identiques et courtes? A la limite, on obtient une distribution déterministe. Autrement dit, en créant une chaîne, vous pouvez réduire la variabilité de la distribution.

Est-il possible d'augmenter la variabilité? C'est facile. Au lieu d'une chaîne de phases, nous utilisons des catégories alternatives, en choisissant au hasard l'une d'entre elles. Un exemple. Presque toutes les demandes sont exécutées rapidement, mais il y a une petite chance qu'une énorme demande arrive, ce qui prend beaucoup de temps. Une telle distribution aura un taux d'échec décroissant. Plus nous attendons, plus il est probable que la demande entre dans la deuxième catégorie.



En continuant à développer la méthode des phases, les théoriciens ont constaté qu'il existe une classe de distributions avec laquelle vous pouvez approcher avec précision une distribution arbitraire non négative! La distribution de Coxian est construite par la méthode des phases, seulement nous ne sommes pas obligés de passer par toutes les phases, après chaque phase il y a une certaine probabilité d'achèvement.



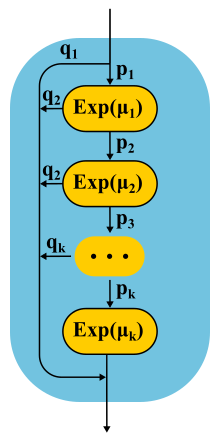
Ce type de distribution peut être utilisé à la fois pour générer un flux d'entrée non-Poisson et pour créer un temps de service non exponentiel. Voici, par exemple, la chaîne de Markov pour le système M / E2 / 1 avec distribution Erlang pour le temps de service. L'état est déterminé par une paire de nombres (n, s), où n est la longueur de la file d'attente, et s est le numéro de l'étape où se trouve le serveur: premier ou deuxième. Toutes les combinaisons de n et s sont possibles. Les messages entrants ne changent que n, et à la fin des phases, ils alternent et diminuent la longueur de la file d'attente après la fin de la deuxième phase.

Vous avez des microrafales!

Un système chargé de la moitié de sa capacité peut-il ralentir? En tant que premier sujet de test, nous préparons M / G / 1. Éléments fournis: écoulement de Poisson à l'entrée et distribution arbitraire du temps de service. Considérez le chemin d'une demande unique à travers l'ensemble du système. Une requête entrante entrante au hasard voit dans la file d'attente devant elle le nombre moyen de requêtes $$$\ mathbf {E} [N_Q]$ . Le temps de traitement moyen pour chacun d'eux $$$\ mathbf {E} [S]$ . Avec une probabilité égale à l'élimination $$$\ rho$ , il y a une autre demande dans le serveur, qui doit d'abord être "traitée" à temps $$$\ mathbf {E} [S_e]$ . En résumé, nous obtenons que le temps d'attente total dans la file d'attente $$$\ mathbf {E} [T_Q] = \ mathbf {E} [N_Q] \ mathbf {E} [S] + \ rho \ mathbf {E} [S_e]$ . Par le théorème de Little $$$\ mathbf {E} [N_Q] = \ lambda \ mathbf {E} [T_Q]$ ; en combinant, nous obtenons:

$$

$$\ mathbf {E} [T_Q] = \ frac {\ rho} {1- \ rho} \ mathbf {E} [S_e]$$

Autrement dit, le temps d'attente dans la file d'attente est déterminé par deux facteurs. Le premier est l'effet de l'utilisation du serveur, et le second est le temps moyen après service. Considérez le deuxième facteur. Une demande arrivant à un moment donné $$$t$ , voit que le suivi prend du temps $$$S_e (t)$ .



Temps moyen $$$\ mathbf {E} [S_e]$ déterminé par la valeur moyenne de la fonction $$$S_e (t)$ , c'est-à-dire l'aire des triangles divisée par le temps total. Il est clair que nous pouvons nous limiter à un triangle «médian», puis $$$\ mathbf {E} [S_e] = \ mathbf {E} [S ^ 2] / 2 \ mathbf {E} [S]$ . C'est assez inattendu. Nous avons reçu que le temps de service après-vente est déterminé non seulement par la valeur moyenne du temps de service, mais aussi par sa variabilité. L'explication est simple. La probabilité de tomber dans un long intervalle $$$S$ de plus, elle est en fait proportionnelle à la durée S de cet intervalle. Cela explique le fameux Paradoxe des temps d'attente, ou Paradoxe d'inspection. Mais revenons à M / G / 1. Si vous combinez tout ce que nous avons obtenu et réécrivez en utilisant la variabilité $$$C ^ 2_S = \ mathbf {E} [S] / \ mathbf {E} [S] ^ 2$ obtenez la fameuse formule Pollaczek-Khinchine :

$$

$$\ mathbf {E} [T_Q] = \ frac {\ rho} {1- \ rho} \ frac {\ mathbf {E} [S]} {2} (C ^ 2_S + 1)$$

Si la preuve vous ennuyait, j'espère qu'elle plaira au résultat de son application dans la pratique. Nous avons déjà examiné les données de temps de service dans RTMR. La longue queue apparaît juste avec une grande variabilité, et dans ce cas $$$C ^ 2_S = 381$ . Vous voyez, c'est bien plus que $$$C ^ 2_S = 1$ pour la distribution exponentielle. En moyenne, tout est super rapide: $$$\ mathbf {E} [S] = 263,792 μs$ . Supposons maintenant que le RTMR soit modélisé par le système M / G / 1, et que le système ne soit pas lourdement chargé, $$$\ rho = 0,5$ . En substituant à la formule, on obtient $$$\ mathbf {E} [T_Q] = 1 * (381 + 1) / 2 * 263,792 μs = 50 ms$ . En raison des microrafales, même un système aussi rapide et sous-utilisé peut se transformer en moyenne en un système dégoûtant. Pendant 50 ms, vous pouvez aller sur le disque dur 6 fois ou, si vous avez de la chance, même dans un centre de données sur un autre continent! Soit dit en passant, pour G / G / 1, il existe une approximation qui prend en compte la variabilité du trafic entrant: il a exactement la même apparence, mais à la place $$$C ^ 2_S + 1$ c'est la somme des deux variétés $$$C ^ 2_S + C ^ 2_A$ . Dans le cas de plusieurs serveurs, les choses vont mieux, mais l'effet de plusieurs serveurs n'affecte que le premier facteur. L'effet de la variabilité demeure: $$$\ mathbf {E} [T_Q] ^ {G / G / k} ≈ \ mathbf {E} [T_Q] ^ {M / M / k} (C ^ 2_S + C ^ 2_A) / 2$ .

À quoi ressemblent les microrafales? En ce qui concerne les pools de threads, ce sont des tâches qui sont traitées assez rapidement pour ne pas être visibles dans les planifications de recyclage, et suffisamment lentes pour créer une file d'attente derrière elles et affecter le temps de réponse du pool. D'un point de vue théorique, ce sont d'énormes requêtes de la part de la distribution. Disons que vous disposez d'un pool de 10 threads et que vous regardez le programme de recyclage, basé sur les métriques de temps de fonctionnement et d'indisponibilité, qui sont collectées toutes les 15 secondes. Tout d'abord, vous ne remarquerez peut-être pas qu'un thread est suspendu, ou que les 10 threads ont effectué simultanément de grandes tâches pendant une seconde, puis n'ont rien fait pendant 14 secondes. Une résolution de 15 secondes ne permet pas de voir un saut d'utilisation jusqu'à 100% et de retour à 0%, et le temps de réponse en souffre. , , 15 6 , .



, ( ) .

, RTMR SelfPing, ( 10 ), — . , 10 15 . , . , , 10 , , — . self-ping- CPU. , : , , . : , , . : . , 15- , — .

, , SelfPing , ? ? , LWTrace. , . -100 . . : ; — , , ; perf , , .

« », . , , . FIFO-. , , latency ( SPT SRPT). — . , , , . , « », .

, - product-form solution . M/ Cox /1/ PS . , (Coxian distribution) (Processor Sharing), , , . ? , . , , (. ) , , M/ M /1/ FIFO , , .

! , , , ! insensitivity property. , , , , . — M/M/∞. , . , product-form solution — BCMP .

. , (, ), , , ó . . . $$$\mathbf{E}[T] = 1/3 \mathbf{E}[T_1] + 2/3 \mathbf{E}[T_2]$ . $$$\mathbf{E}[T_i] = 1/(\mu_i - \lambda_i)$ M/M/1/FCFS $$$\mathbf{E}[T] = 1/3 * 1/(3 - 3 * 1/3) + 2/3 * 1/(4 - 3*2/3) = 0.5$ .

, , . , .

1. , , , computer science, . Performance Modeling and Design of Computer Systems: Queueing Theory in Action (2013). - , . ó — .
2. , , , , Robert B. Cooper. , .