Théorie du bonheur. Les accidents ne sont pas accidentels?

Je continue de familiariser les lecteurs de Habr avec les chapitres de son livre "Theory of Happiness" avec le sous-titre "Mathematical Foundations of the Laws of Meanness". Ce livre de science populaire n'est pas encore publié, racontant de manière très informelle comment les mathématiques vous permettent de regarder le monde et la vie des gens avec un nouveau degré de conscience. C'est pour ceux qui s'intéressent à la science et pour ceux qui s'intéressent à la vie. Et puisque notre vie est complexe et, dans l'ensemble, imprévisible, l'accent dans le livre est principalement sur la théorie des probabilités et les statistiques mathématiques. Ici les théorèmes ne sont pas prouvés et les fondements de la science ne sont pas donnés, ce n'est en aucun cas un manuel, mais ce qu'on appelle la science récréative. Mais c'est précisément une telle approche presque ludique qui nous permet de développer l'intuition, d'égayer les cours pour les étudiants avec des exemples vivants et, enfin, d'expliquer aux non-mathématiciens et à nos enfants ce que nous avons trouvé si intéressant dans notre science sèche.



Dans ce chapitre, nous discutons du vol de pièces prédéterminé, des cartes topographiques, des catastrophes mathématiques et de la nature de l'aléatoire. Et en cours de route, regardons des sections de mathématiques telles que la théorie des mesures et la théorie du chaos dynamique.

La conversation sur les lois de la méchanceté, en tant que source d'agitation quotidienne, commence souvent par la fameuse loi du sandwich . Il est simplement formulé, facilement vérifiable et largement connu:

Un sandwich laisse toujours tomber le beurre.

Il est clair que le mot "toujours" ici est une exagération. Il est facile d'imaginer les conditions dans lesquelles un sandwich tombera, laissant le côté huilé intact. Qu'est-ce que les gens entendent par cette loi? Très probablement, le sandwich tombe le beurre assez souvent pour le rendre visible. Mais un résultat défavorable d'une baisse est-il plus probable qu'un résultat favorable? Les sandwichs sont différents, ils tombent dans des circonstances différentes, de hauteurs différentes ... Il y a tellement de paramètres qu'il est probablement inutile de parler de modèles dans une telle tâche. Tout peut arriver. Il arrive qu'il tombe dans l'huile, puis il devient insultant, on se souvient de la loi et on s'en souvient. Et si le sandwich n'est pas intéressant - avec l'huile vers le haut, ou s'il s'avère qu'il n'y en a pas du tout, il n'y a rien à dire - il est clair que la loi est comique! Au final, un sandwich est comme une pièce de monnaie, que les mathématiciens utilisent pour obtenir des variables aléatoires avec deux valeurs possibles: «aigle» et «queues». Si la pièce est «honnête», peu importe de quel côté tomber, et nous disons que la probabilité de chute de l'aigle et de la queue est la même et la même $$$1/2$ . En théorie, les sandwichs devraient être les mêmes. Nous y reviendrons dans le chapitre suivant, mais pour l'instant jetons un coup d'œil au système probabiliste le plus probable - la pièce.

Une pièce dans des expériences théoriques de probabilité est lancée d'une manière magique spéciale, de sorte que le choix de la position initiale, de la vitesse initiale et de la vitesse de rotation pendant le lancer n'affecte pas la probabilité d'un résultat spécifique. Mais c'est évident que c'est impossible! La pièce est un système mécanique et obéit aux lois de la mécanique, mais elles ne contiennent pas de variables aléatoires. L'avenir des lois du mouvement d'un corps aussi simple qu'une pièce de monnaie est uniquement déterminé par l'état passé de ce corps. Si un robot lance une pièce ou si le démon de Laplace est une créature mythique qui possède des informations complètes sur les coordonnées et les vitesses de tout système mécanique, des résultats identiques seront obtenus avec des données initiales constantes. Nous ne sommes bien sûr pas des robots ou des démons, mais les gens jettent-ils vraiment des pièces si bâclées et imprévisibles que les lois de la mécanique peuvent conduire à des accidents?

Et d'où vient, en général, le hasard dans le monde décrit par les lois de la mécanique? D'où vient le hasard? Quelle est la différence entre des systèmes vraiment chaotiques ou stochastiques, fondamentalement imprévisibles, et des systèmes dans lesquels il est tout simplement difficile de deviner le comportement, mais il peut être calculé?

Le problème des pièces a été étudié en 1986 par Joseph Keller. Nous fournissons une explication simple de l'occurrence de l'incertitude dans ce processus, basée sur le raisonnement de l'article de Keller. De quel côté la pièce tombera dépend de son temps de vol. $$$t$ et de la vitesse angulaire $$$\ omega$ . Si vous mesurez la vitesse angulaire en tours par unité de temps, alors le nombre de tours effectués par la pièce est exprimé très simplement $$$n = t \ omega$ . Cette dépendance définit les lignes d'un nombre égal de révolutions dans les coordonnées $$$(t, \ oméga)$ et elles limitent à leur tour les zones correspondant à un nombre pair et impair de révolutions.

Un diagramme montrant la parité du nombre de tours effectués par une pièce en vol. Le rectangle indique la zone dans laquelle se déroule le plus souvent le processus de diseuse de bonne aventure sur la pièce.

Dans un tel diagramme, il est possible de montrer quel sera le résultat d'un lancer de pièce, tordu par un nombre connu de tours par seconde, et pris après un temps de retournement connu. Si nous tombons dans une bande blanche, alors le même côté tombera qui était sur le dessus lors du lancer, s'il est orange - le contraire. Les lignes de vitesse égale sont des hyperboles et on peut voir qu'à mesure que la vitesse augmente, l'alternance de zones devient de plus en plus fréquente et les zones elles-mêmes deviennent plus minces. La main humaine est imparfaite et une très petite dispersion des valeurs initiales couvre de nombreux domaines à la fois, ce qui rend le résultat imprévisible. Dans la plage de la main (le rectangle dans le diagramme), un décalage de suffisamment $$$5 \%$ pour passer d'une bande blanche à une orange. La question demeure: comment «l'honnêteté» d'une véritable pièce mécanique découle-t-elle de cette construction? Comment obtenir la probabilité de perte d'un aigle ou de queues à partir du diagramme résultant?

Agissez de toute urgence!

Nous nous plongerons un peu dans ces mathématiques qui ne sont pas enseignées à l'école afin de mieux comprendre ce dont nous discutons. Nous avons dit dans l' introduction que les mathématiciens n'étudient pas les nombres ou les formes géométriques, comme cela peut sembler après avoir étudié un cours scolaire. Ils travaillent avec des structures mathématiques (algèbres abstraites, demi-anneaux, champs, monoïdes, espaces topologiques et autres trucs abstraits), les décrivent, semble-t-il, complètement indépendants de la pratique, les définissent, étudient leurs propriétés, prouvent des théorèmes. Et ensuite, ils perfectionnent leurs compétences pour trouver de telles structures dans divers domaines de la connaissance, réalisant des percées incroyablement utiles, y compris dans des domaines purement appliqués. Nous allons maintenant aborder un peu ces mathématiques et examiner comment la base de la théorie des probabilités est construite sur la base d'un concept de mesure très abstrait.

Nous avons décrit la mécanique de la pièce et obtenu des zones qui décrivent des ensembles de solutions avec certaines propriétés. Les zones sont des figures plates, comment passer de celles-ci aux probabilités correctement? Nous devons mesurer nos zones et nous arrivons naturellement à leur zone. Aire - est une mesure d'une figure plate. Il s'agit d'un terme mathématique exact pour une fonction qui associe un ensemble à une certaine valeur numérique non négative. Des exemples de mesures sont les quantités dans les ensembles énumérés (le nombre de pommes dans un sac, par exemple), ainsi que la longueur , la superficie et le volume des chiffres .

Il y a toute une section en mathématiques appelée théories de la mesure . Cette théorie est née au tournant des XIXe et XXe siècles (Emil Borel et Henri Lebesgue étaient à ses origines) et a ouvert aux mathématiciens de nombreuses possibilités d'analyser des objets très complexes: ensembles de chants et de fractales. Il a constitué la base de l'analyse fonctionnelle et de la théorie moderne des probabilités, dont le fondement a été posé par le remarquable mathématicien russe Andrei Kolmogorov. La définition de la probabilité, en tant que mesure, vous permet de voir toutes les propriétés de base de la probabilité pour les ensembles discrets et continus.

Bien que notre livre ne soit pas un manuel, il vaut la peine de s'arrêter un peu pour regarder les concepts de probabilité du thorium à vol d'oiseau et pour ressentir le goût des mathématiques. Pour commencer, nous énumérons les principales propriétés de toute mesure. Afin de mieux les imaginer, vous pouvez utiliser les mots «quantité» ou «longueur» ou «surface» au lieu du mot «mesure».

1. La mesure de l'ensemble vide est zéro.
2. La mesure de l'ensemble mesurable est finie pour les mesures finies.
3. La mesure du sous-ensemble ne dépasse pas la mesure de l'ensemble
4. La mesure d'union de deux ensembles arbitraires est égale à la somme des mesures de ces ensembles moins la mesure de leur intersection (additivité).
5. La mesure de complémentation d'un sous-ensemble est égale à la différence entre les mesures de l'ensemble et la mesure du sous-ensemble.

Une fonction numérique non négative peut-elle être une mesure? Pas du tout. Par exemple, l'âge donne à une personne un numéro complètement spécifique. Mais l'âge de deux personnes ne peut pas être défini comme la somme de leur âge. Et la vitesse de course n'est pas une mesure - deux personnes ne courent pas deux fois plus vite. Mais l'élan (élan) ou l'énergie a déjà les propriétés d'une mesure. Le poids, la somme d'argent, la quantité de connaissances, le volume du cri, bien que les choses ne soient pas toujours facilement mesurables, peuvent également servir de mesure pour de nombreuses personnes.

Sur un plan intuitif, presque tout le monde connaît maintenant le concept de probabilité. Il est estimé par les politologues et les journalistes dans les talk-shows, il est question du réchauffement climatique ou de la pluie de demain, des blagues à ce sujet sont racontées: Quelle est la probabilité de rencontrer un dinosaure sur le Tver? - Une seconde: soit une réunion ou non. En mathématiques modernes, le concept de probabilité est défini comme une mesure sur un ensemble spécial appelé espace de probabilité . Il comprend à la fois les événements élémentaires et leurs combinaisons obtenues à l'aide des opérations d'union, d'intersection et d'exclusion. Un exemple d'événement élémentaire: «perte d'un triple lors du lancement d'un os». Un exemple d'événement qui n'est pas élémentaire: "la perte d'un nombre pair sauf deux". Donc, nous listons les propriétés de probabilité:

1. La probabilité d'un événement impossible est nulle.
2. La probabilité pour tout l'espace de probabilité est égale à l'unité.
3. Si un événement en implique également un autre, la probabilité du second ne dépasse pas la probabilité du premier. Ici, la relation «implique» pour les événements est équivalente à «est un sous-ensemble» pour les ensembles et ne signifie pas «est une cause».
4. La probabilité d'occurrence d'au moins un des deux événements arbitraires est égale à la somme des probabilités de chacun de ces événements, moins la probabilité que les événements se produisent simultanément.
5. La probabilité qu'un événement ne se produise pas est un moins la probabilité qu'un événement se produise.

Examinez de plus près les propriétés des mesures et des probabilités et vous verrez que nous parlons des mêmes propriétés.

Toutes les propriétés de probabilité ne découlent pas de sa définition en tant que mesure: les concepts d'indépendance des événements et la méthode de calcul de la probabilité de deux événements indépendants ou plus simultanément en tant que produits de probabilités sont introduits par la probabilité conditionnelle , mais ces concepts sont cohérents avec la définition de Kolmogorov.

Les variables aléatoires discrètes correspondent à des ensembles dénombrables finis; en eux, une mesure naturelle est un décompte ordinaire du nombre d'éléments. Par conséquent, la probabilité dans un espace probabiliste discret est le calcul combinatoire d'options qui est familier à chaque élève. Pour les variables aléatoires continues, la probabilité, en tant que mesure, ressemble plus à la longueur ou à l'aire, et nous parlons ici de densités de probabilité .

L'analogie des probabilités avec la mesure ne s'arrête pas là. Quelle est la valeur moyenne ? Il s'agit d'un analogue de la position du centre de masse d'une figure constituée de masses ponctuelles ou d'un solide de densité connue. Et ces quantités sont calculées de la même manière. Et comment la dispersion des variables aléatoires autour de la moyenne est-elle caractérisée: variance ? Tout comme le moment d'inertie caractérise la répartition de la masse autour du centre de masse. Et encore une fois, les formules de calcul de la variance pour un échantillon ou une distribution coïncident avec les formules du moment d'inertie d'un ensemble de corps ou d'un corps solide d'une forme rusée.

Soit dit en passant, si nous remplaçons dans les définitions et propriétés de probabilité la somme par «maximum» et le produit par «minimum», alors nous pouvons construire une théorie alternative, elle s'appelle la théorie des possibilités . Voilà comment les mathématiques fonctionnent. Nous commençons par un raisonnement abstrait: les nombres forment une algèbre avec des opérations d'addition et de multiplication, mais sur un intervalle de nombre limité, vous pouvez construire une algèbre similaire avec des opérations de minimum et de maximum. Nous construisons le concept de mesure sur une nouvelle algèbre et découvrons qu'elle ouvre une nouvelle vision du monde! Contrairement à la théorie des probabilités, dans une telle théorie, deux mesures coordonnées peuvent être construites - la possibilité et le besoin , et, contrairement à la probabilité, elles sont en bon accord avec les opérations d'union et d'intersection des événements. Cette direction a été créée par l'Américain Lotfi Zadeh, un Azerbaïdjanais d'origine, sert de base à la logique floue et est utilisée dans les systèmes de reconnaissance automatique de formes et de prise de décision.

Incroyable, mais vrai!

La première propriété des mesures semble banale, mais elle est intéressante par son asymétrie. Si la mesure du sous-ensemble est nulle, cela ne signifie pas qu'il est vide! Par exemple, une ligne est un sous-ensemble des points d'un plan, mais sa zone (mesure) est nulle. Il existe des exemples plus exotiques - des ensembles de Cantor et de fractales, ayant une structure complexe, contenant un nombre infini de points, «occupant» visuellement une certaine zone ou un certain volume, mais ayant néanmoins une mesure nulle.

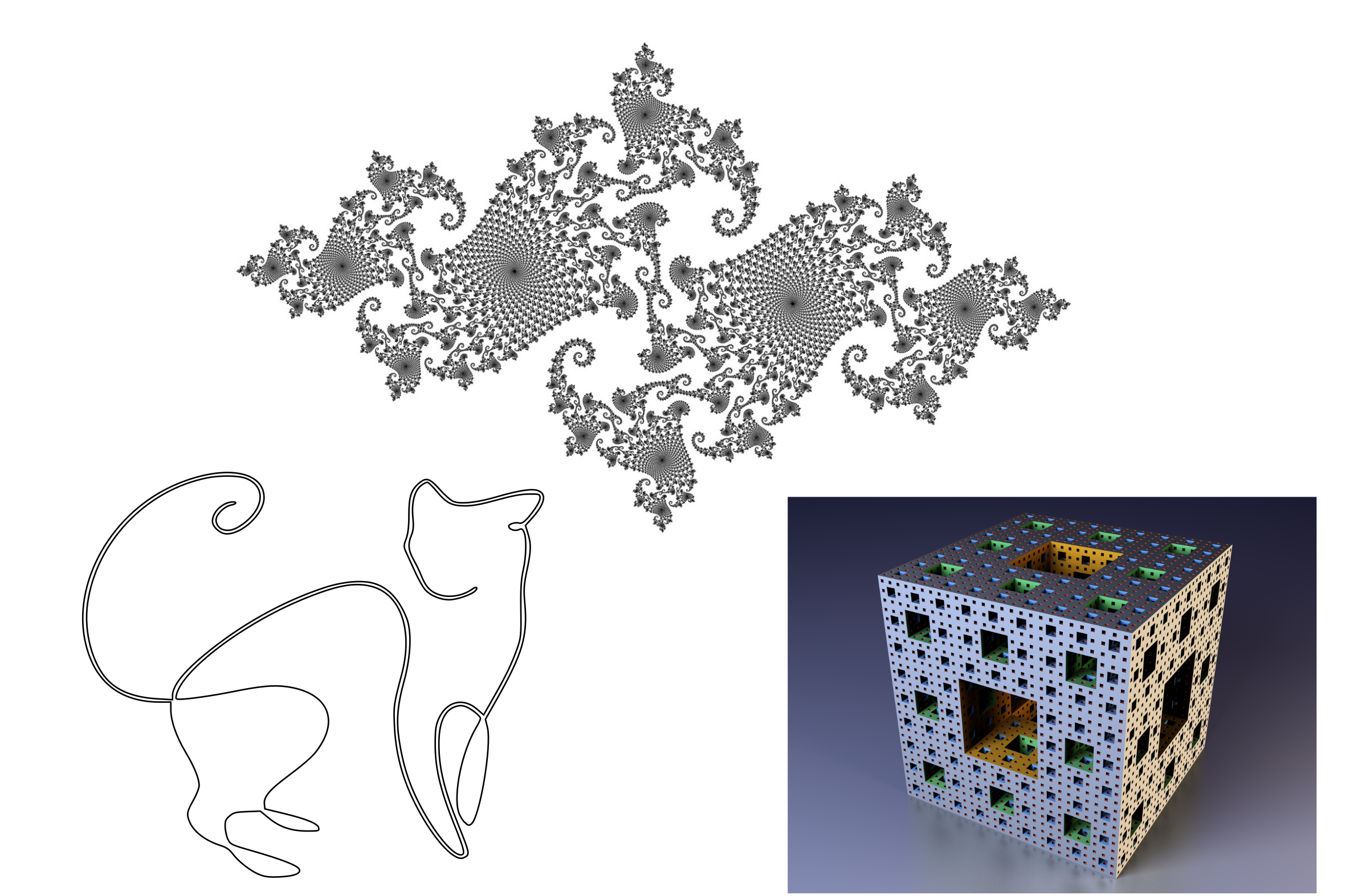Quelques objets de mesure nulle: une ligne dans un avion, un ensemble sporadique de Julia, une éponge fractale de Menger.

En préparant cette illustration, j'ai trouvé une merveilleuse image d'un ensemble déconnecté de Julia sur un fond transparent à haute résolution. Après l'avoir inséré dans l'éditeur de vecteur, je suis tombé sur une drôle de difficulté - il était très difficile d'accéder à cette image avec la souris pour la sélectionner. Il est si «lâche» que la probabilité de pénétrer dans un pixel plein était sensiblement inférieure à celle de pénétrer dans un arrière-plan transparent. Dans l'espace des probabilités, des sous-ensembles de mesure zéro peuvent également exister, mais cela ne signifie pas que les événements de ces sous-ensembles sont impossibles. De la quatrième à la cinquième tentative, je pouvais toujours sélectionner l'image, car les pixels ont une taille finie. Mais que se passerait-il si je mettais à ma disposition un véritable ensemble incohérent de Julia à résolution infinie?

Imaginez que vous utilisez un générateur de nombres aléatoires logiciel qui produit un nombre réel arbitraire à partir de $$$0$ avant $$$1$ . Quelle est la probabilité qu'un nombre tombe? $$$0$ ? et chiffres $$$1/2$ ou $$$e / \ pi$ ? Dans tous ces cas, la réponse sera - zéro! Il s'agit plutôt du plus petit nombre positif disponible pour l'ordinateur, la machine dite epsilon, car l'ordinateur fonctionne avec un nombre fini de décimales. Attendez, dites-vous, dans quel sens est zéro? Les mêmes chiffres ne sont pas impossibles. Conduisons une expérience, par conséquent nous obtenons un certain nombre spécifique, et quand nous l'obtenons, alors «par construction» la probabilité de son apparition ne peut pas être nulle. C'est vrai, mais combien de temps dois-je attendre jusqu'à ce que exactement 0 tombe? Presque sans fin! Le fait est qu'un seul nombre, comme un point sur un segment, a une mesure nulle et une probabilité zéro honnête. Seule une mesure d'un segment continu, même très petit, est non nulle. Nous ne parlons donc pas de probabilité, mais de densité de probabilité qui, multipliée par une mesure finie d'un sous-ensemble dans un espace de probabilité, donnera une valeur finie - la probabilité de tomber dans ce sous-ensemble. Soit dit en passant, s'avérer être notre générateur de nombres aléatoires idéal avec une précision infinie, la probabilité d'obtenir un certain nombre rationnel (pas du béton, mais n'importe lequel) avec lui sera également nulle. La preuve que les nombres rationnels forment un sous-ensemble dense de mesures nulles de l'ensemble des nombres réels a fait du bruit à la fin du XIXe siècle.

Si quelqu'un mène patiemment mille expériences avec une pièce de monnaie et vous dit joyeusement qu'il a eu autant d '«aigles» que de «queues», vous pouvez sans risque exprimer un doute ou le féliciter pour sa chance rare. Bien que jetant une pièce et un processus aléatoire discret, à mesure que les statistiques s'accumulent, la puissance de l'espace de probabilité augmentera et la mesure de l'événement: «le nombre d '« aigles »coïncide avec le nombre de« queues »» diminuera. On peut montrer, en utilisant la formule de Stirling, que la probabilité de cet événement «le plus probable» tend vers zéro avec une augmentation du nombre de tests $$$1 / \ sqrt {\ pi n}$ . Pour une centaine de lancers, c'est un peu plus de cinq pour cent, pour dix mille - seulement un demi pour cent. Dans de tels cas, les mathématiciens disent: presque certainement le nombre «d'aigles» ne sera pas égal au nombre de «queues» . Aussi étrange que cela puisse paraître, mais «presque certainement» est un terme mathématique exact, ce qui signifie que l'événement est un complément à un sous-ensemble de l'espace de probabilité de mesure nulle. Nous reviendrons sur ces considérations dans l'un des chapitres suivants, lorsque nous nous poserons la question: dans quelle mesure chacun de nous peut-il se considérer comme normal.

Vérifier l'honnêteté d'une vraie pièce

Revenons à la pièce et à son honnêteté. La définition de Kolmogorov de la probabilité a concilié sa définition de fréquence (comme la fréquence relative des événements qui se produisent) et géométrique (comme une fraction du "volume" d'un événement dans le "volume" total des possibilités). Ainsi, la fraction de l'aire des bandes blanches dans le diagramme calculée pour une pièce tournante reflète la probabilité de tomber du même côté auquel nous l'avons jetée.

Mais le problème! L'aire de chaque bande de notre diagramme est infinie (si l'on considère le quart entier du plan de coordonnées). Cependant, l'additivité de la mesure nous permettra de montrer avec précision que cela n'empêche pas que les zones des zones ombrées et blanches soient identiques. Sous forme explicite, les équations de nos courbes ont la forme$$$\omega = n/t$ . Si l'aire sous la courbe $$ω = 1 / t est égal$\omega = 1/t$$$S , puis en raison de la propriété d'additivité, l'aire sous la courbe$S$$$ω = n / t sera égal$\omega = n/t$$$$S_n = n S$ . À son tour, pour les bandes individuelles, nous obtenons: $$$S_{n} - S_{n-1} = n S - (n-1)S = S$ .Il s'avère que la différence de surface ne dépend pas du "nombre" de l'hyperbole. Ce n'est pas quelque chose de spécial concernant les hyperboles; la même conclusion peut être tirée pour n'importe quelle courbe de la forme$$y = n f ( x ) , si seulement la fonction$y = n f(x)$$$f était mesurable. Et si c'est le cas, alors pour toute la zone de définition, entrer dans la partie blanche du diagramme ou dans l'ombre est tout aussi probable, comme prévu pour une pièce «honnête». Les arguments que nous venons de citer semblent assez simples, mais ils donnent un résultat très général, applicable à toute quantité additive. Le concept abstrait de mesure nous a permis de comparer des quantités infinies entre elles, tout en restant dans le cadre de la logique et du bon sens. L'abstraction est bonne, mais on peut affirmer qu'en réalité, nous ne jetons pas de pièces avec tous les paramètres possibles. Comme l'ont montré des expériences avec une caméra à grande vitesse, les vitesses angulaires tombent dans$f$



$$20 à$20$$$40 tours par seconde, et la durée du vol est de la moitié à une seconde. Cette zone est mise en évidence par un rectangle dans le diagramme. Dans ce document, la surface totale des rayures blanches est légèrement plus grande que celles orange, et nous pouvons conclure que la probabilité de tomber du même côté que lors du lancer sera$40$$$$50.6\%$ .

En 2007, un groupe de Percy Deaconess et al de Stanford a publié un article qui fournit une analyse détaillée du processus de retournement d'une pièce. Une description détaillée de la mécanique d'un disque volant et rotatif, qui non seulement tourne, mais aussi précède - l'axe de rotation lui-même tourne en vol, montre qu'avec un lancer manuel depuis la position «aigle d'en haut», la probabilité que «l'aigle» tombe d'un centième est plus de la moitié.

Est-ce beaucoup ou peu? De combien d'expériences avez-vous besoin pour faire une telle différence? À mesure que les données expérimentales s'accumulent, l'erreur-type de la moyenne, reflétant l'erreur avec laquelle la valeur moyenne peut être calculée, diminue proportionnellement à la racine carrée du nombre de tests:$$σ μ = σ / √n ici$\sigma_{\mu} = \sigma/\sqrt{n}$$$σ est l'écart type pour la distribution étudiée. Dans notre cas, pour la distribution de Bernoulli avec probabilité$\sigma$$$0,51 qui est égal$0.51$$$$\sqrt{0.51\times0,49}\approx0.5$ . Pour identifier en toute confiance l'écart de la moyenne d'un centième, cet écart doit dépasser $$3 écarts-types. Ainsi, nous pouvons estimer le nombre d'essais:$3$

$$

$$n = \left(\frac{\sigma}{\sigma_{\mu}}\right)^2 = \left(\frac{3\times0.5}{0.01}\right)^2 \approx 22500$$

Tant de fois que vous devez lancer une pièce pour remarquer la prédétermination mécanique du résultat. Pour clarifier ce que l'on veut dire, je donnerai un exemple de deux cents tests de "pièces" idéales et légèrement imparfaites effectués afin de calculer la probabilité de perte, disons, d'un aigle. Chaque test consiste en$$40000 lancers. Les mots «pièce» et «lancer» sont entre guillemets, car en fait ce n'est pas une pièce physique qui a été utilisée, mais un générateur de nombres aléatoires obéissant à la distribution de Bernoulli.$40000$

Expériences de lancer une pièce idéale et légèrement imparfaite afin de corriger l'imperfection.

On voit que seulement après$$20 000 tests du «nuage» de valeurs moyennes observées commencent à se séparer clairement. Eh bien, pour un usage domestique, nous pouvons supposer que la pièce est un bon générateur d'un choix aléatoire de deux options également probables.$20000$

Droit du tourisme

L'équivalence de la détermination géométrique et fréquentielle des probabilités révèle le mystère d'une loi de la méchanceté, connue des touristes, des géologues et de tous ceux qui utilisent les cartes topographiques:

L'endroit où le touriste se rend est le plus souvent soit sur le pli de la carte, soit sur le bord de la feuille.

Supposons que nous nous intéressions également aux objets situés dans toutes les parties de la carte. Mais nous nous intéressons rarement aux objets de mesure nulle - le but de l'utilisation d'une carte est de surveiller les environs de l' objet, c'est-à-dire une zone finie. Qu'une petite fraction nous suffise$$α à partir de la zone de la carte entière$\alpha$$$S pour comprendre comment se rendre à l'objet. Donc, si l'objet s'approche d'un virage ou d'un bord à une distance critique$S$$$d , nous considérerons que la loi sur le tourisme est respectée. La part des zones frontalières dans la zone totale de la carte nous donnera l'occasion de faire l'expérience de cette loi de la méchanceté sur nous-mêmes. Voici à quoi ressemblent les parties désagréables de la carte$d$$$α = 0,5 % et dans un virage.$\alpha=0.5\%$

Le gris indique les "mauvaises" zones. Un tracé avec un demi-pour cent de surface pour une carte de 40 cm de large est montré séparément, il a un diamètre légèrement supérieur à 3 cm.

Pour une carte carrée$$$d = \sqrt{\alpha S}$ . Les bandes désagréables auront une zone $$$d \sqrt{S} = S\sqrt{\alpha}$ .Quatre bandes, deux verticales et deux horizontales, seront situées sur le bord, tout pli supplémentaire, horizontal ou vertical, ajoutera une autre bande. En même temps, les bandes qui se croisent ajoutent des carrés supplémentaires avec une zone$$$d^2 = \alpha S$ . En pliant la carte pour qu'elle se révèle $$$n$ horizontal et $$$m$ les virages verticaux, on obtient la surface totale de la zone désagréable égale à: $$$S (n + 2) \ sqrt {\ alpha} + S (m + 2) \ sqrt {\ alpha} -S (n + 2) (m + 2) \ alpha$ . En le ramenant à la zone de la carte entière, nous obtenons une part désagréable de la surface totale:

$$

$$p = (n + m + 4) \ sqrt {\ alpha} - (n + 2) (m + 2) \ alpha.$$

La figure montre les domaines dans lesquels cette proportion dépasse $$ pour différentes valeurs $$$\ alpha$ .

Zones dans lesquelles il y a une probabilité accrue d'être au pli de la carte ou à sa périphérie. Les nombres indiquent la fraction de la zone du quartier considéré par rapport à la zone de la carte entière.

Il s'avère qu'une carte pliée en deux deux fois peut déjà être formellement considérée comme malhonnête par rapport à un touriste. Le plus souvent, les cartes ont trois plis verticaux et trois horizontaux, ce qui donne la probabilité de respecter la loi de moyenne avec une probabilité d'environ $$$60 \%$ à $$$\ alpha = 0,5 \%$

D'où vient le hasard?

Dans les boutiques de souvenirs, vous pouvez trouver des pendules magnétiques pour le "choix des envies". Ce sont aussi des générateurs aléatoires mécaniques et sont parfois appelés à tort «pendules chaotiques». Commençant le mouvement à partir d'une position et d'une vitesse initiales, le pendule effectue une série d'oscillations «imprévisibles» et s'arrête finalement dans l'un des secteurs. Cependant, les fluctuations ici ne sont pas imprévisibles, elles sont tout simplement très sensibles aux conditions initiales. Pour chaque secteur dans lequel le pendule peut s'arrêter, il y a une région d'attraction dans l'espace de coordonnées-vitesse. Il s'agit d'un ensemble de telles conditions initiales dans lesquelles le pendule attirera nécessairement jusqu'à un certain point dans le secteur indiqué. Le point d'arrêt du pendule est appelé un attracteur - un point d'attraction. Dans le cas d'un pendule de l'image, l'espace des coordonnées et des vitesses est quadridimensionnel et il n'est donc pas facile de montrer la zone d'attraction. Mais si nous nous limitons à seulement deux secteurs et réduisons le problème à unidimensionnel (un tel pendule est appelé l'oscillateur Duffing), alors l'espace des valeurs initiales se transformera en plan, de sorte que les régions d'attraction puissent être vues. Ils ressemblent à un symbole complexe de Yin-Yang, se transformant rapidement en bandes étroites qui séparent les zones d'attraction.

Zones d'attraction d'attracteurs pour un pendule unidimensionnel de désirs - l'oscillateur Duffing.

Comme dans le cas de la pièce, en décalant légèrement les conditions initiales, on passe d'un attracteur à un autre. Les dés et la roulette fonctionnent de la même manière, mais ils ne sont pas eux-mêmes des générateurs aléatoires. Ce ne sont pas vraiment des systèmes chaotiques et leur comportement peut être calculé avec précision.

Mais quelle est la vraie chance? Un bon exemple d'un véritable système stochastique est l'apparition de voitures sur la route. Les gens ne sont pas d'accord, ne coordonnent pas leurs plans, chaque élément de l'ensemble en dehors de la route agit indépendamment. Et bien qu'il existe certains modèles dans le comportement des gens - heures de pointe le matin et le soir, routes vides la nuit, etc., nous n'avons pas et n'aurons jamais assez d'informations sur chaque participant au mouvement pour prédire l'apparition de l'un d'eux. La mécanique des particules élémentaires au niveau quantique, la désintégration des atomes instables, les changements dans le code génétique, très probablement, les tremblements de terre et les cotations boursières en bourse sont également stochastiques. La seule chose qui reste au chercheur est de les considérer comme des variables aléatoires et de les décrire en termes de théorie des probabilités.

Mais il y a une autre source de chance: le chaos dynamique . Les systèmes chaotiques diffèrent des systèmes stochastiques en ce qu'ils sont décrits par des équations et des paramètres exacts qui ne contiennent pas d'aléatoire. Cependant, leur comportement n'est pas seulement compliqué, mais chaotique et vraiment imprévisible. Si nous commençons à faire osciller le pendule des désirs, très soigneusement, avec une fréquence et une amplitude contrôlées avec précision, nous constaterons que ses mouvements fluides ne peuvent pas être calculés pendant longtemps. Aucun algorithme sur des ordinateurs arbitrairement précis ne nous permettra de calculer le comportement exact du pendule dans un avenir arbitrairement éloigné. Il ne s'arrêtera à aucun secteur, mais effectuera des mouvements fluides, mais il ne reviendra jamais deux fois au même point dans l'espace de vitesse de coordonnées. Un autre exemple d'un système chaotique extrêmement simple est une balle idéale rebondissant dans le champ de gravité sur une table idéale avec un ressort. Les équations de Lorentz relativement simples ont montré que nous ne pouvons jamais prédire le temps pendant plus de deux semaines - c'est aussi un système chaotique.

La théorie du chaos dynamique a pu expliquer la nature d'une telle imprévisibilité. Le pendule unidimensionnel simple des désirs, que nous avons examiné, avait deux points stationnaires stables - deux attracteurs, et un instable, dont le système essaie de s'éloigner, il est indiqué par un cercle blanc. Dans le mode chaotique, au lieu d'un ensemble d'attracteurs, un nombre infini de trajectoires stationnaires instables apparaissent dans le système. Cet ensemble est infini, mais a une mesure nulle , et est une structure disjointe très compliquée. Une fois sur l'une de ces trajectoires, il est en principe impossible de la suivre à l'aide d'algorithmes finis. Mais le plus surprenant, il s'est avéré que ce nombre infini de trajectoires instables en lui-même est séduisant! 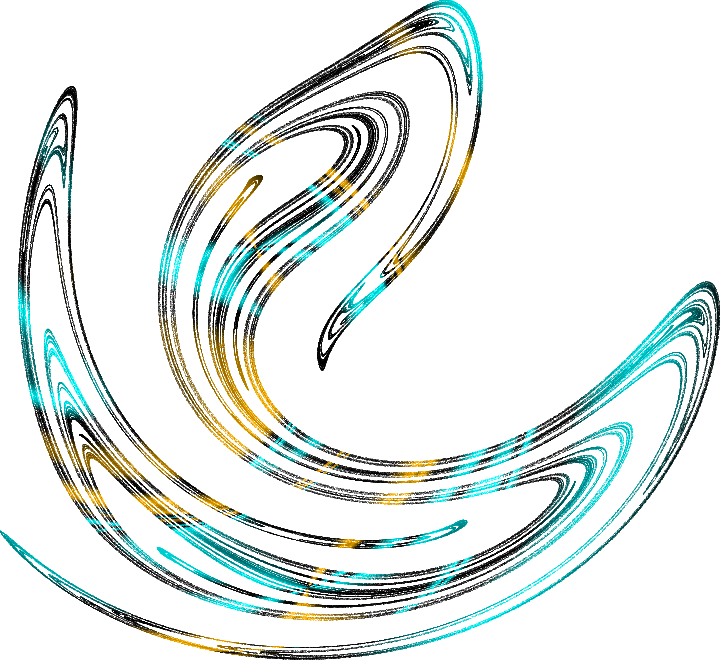Le système chaotique saute continuellement du voisinage d'une trajectoire instable à l'autre, tout en restant dans les limites de cet étrange attracteur. Donc, ces ensembles sont appelés: attracteurs étranges . C'est ainsi que la section d'un attracteur étrange pour un pendule de désirs, soumis à des oscillations harmoniques, est d'une beauté fascinante. Cet objet pour un pendule unidimensionnel peut être décrit dans un espace tridimensionnel (coordonnées, vitesse, phase d'oscillation forcée). Si vous coupez un attracteur dans cet espace par un avion, vous pouvez voir sa structure, c'est ce qu'on appelle la section Poincaré . Chaque point ici est une trace de la trajectoire, et la couleur des points reflète la vitesse relative avec laquelle les trajectoires se dispersent les unes des autres. Voici quelques beaux attracteurs étranges:


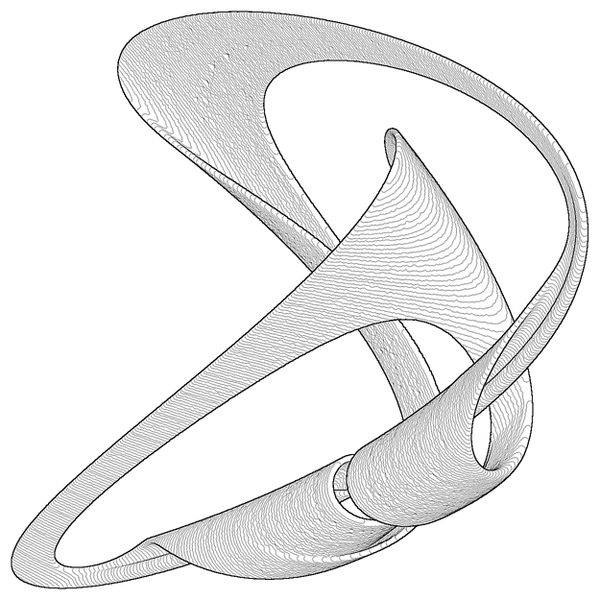À gauche: section Poincare pour la trajectoire d'une balle qui rebondit sur une table à ressort. De nombreux points appartiennent à la surface de la sphère correspondant à la loi de conservation de l'énergie. À droite: une région volumétrique qui renferme un étrange attracteur qui naît lors des vibrations forcées d'une plaque épaisse.

La douceur de la trajectoire chaotique vous permet de regarder un peu vers l'avenir. Cela explique une observation ennuyeuse: d'une part, les prévisionnistes ne peuvent parfois pas prédire la météo en toute confiance pendant une semaine, mais d'autre part, si vous dites que demain sera le même temps qu'aujourd'hui, alors vous ne vous tromperez pas dans environ trois cas sur quatre. . De manière générale, les blagues sur les météorologues sont injustes et nous devons rendre hommage à la pensée humaine et à la persévérance, qui ont permis de prédire la météo à un niveau moderne!

Le chaos dynamique est très complexe et beau en théorie, il donne naissance à des images d'une élégance étonnante, mais il peut aussi être utile. Par exemple, les algorithmes par lesquels des nombres aléatoires sont générés dans les ordinateurs sont également déterministes. Pour les exemples de ce livre, j'ai utilisé un générateur de nombres pseudo-aléatoires qui n'a pas démarré le véritable processus stochastique (décroissance alpha ou comptage des voitures sur la route), mais a calculé le nombre "aléatoire" suivant en fonction des précédents qu'il avait reçus plus tôt.

Des pièces aux papillons et au destin

L'observation de la façon dont les petits écarts se transforment en changements globaux dans le système conduit à penser à «l'effet papillon». Permettez-moi de vous rappeler que cet effet signifie une chaîne de conséquences dramatiques d'une grande portée à la suite d'un événement insignifiant, à première vue. Écrasé par des chercheurs du passé, le papillon de la nouvelle de Ray Bradbury «And the Thunder strike» a conduit à une restructuration radicale de l'avenir. Et une de ses conférences, Edward Lorenz, créateur de la théorie du chaos dynamique, intitulée: "Un battement d'aile de papillon au Brésil peut-il provoquer une tornade au Texas?"

Nous faisons implicitement référence à cet effet, déplorant: "Si je n'avais pas tourné le coin, tout aurait été différent!", "S'il n'avait pas embarqué dans ce train, il n'y aurait pas eu de catastrophe!" ou "À cause de telles bagatelles, ils se sont disputés et se sont séparés !!" Mais nous voyons qu'un monde quantique vraiment stochastique et des horloges atomiques ultra-précises coexistent dans le monde, des systèmes hamiltoniens stables dans le monde des étoiles et des galaxies et le chaos des anneaux de Saturne ou des anneaux de Kuiper, le mouvement thermique des molécules et l'incroyable précision du fonctionnement des systèmes biologiques ou des mécanismes automobiles. Non, le volet d'une aile de papillon ne provoque pas d'ouragans, mais disparaît sans laisser de trace, donnant naissance à une chaîne de tourbillons qui transmettent l'énergie et l'information à des tourbillons de plus en plus petits, jusqu'à ce que l'énergie et l'information disparaissent dans le chaos des fluctuations. Il faut bien comprendre que de petits écarts ne conduisent à une restructuration fondamentale du système que s'il est instable ou si le système est au bord d'une bifurcation ou d'une catastrophe - c'est ainsi que les changements globaux dans le comportement du système sont appelés dans le langage des mathématiques avec de petits changements de paramètres. Et les bifurcations forment toujours des ensembles de mesures nulles dans l'espace des paramètres - ce sont des points ou des limites. Les petites perturbations ne conduisent pas à des catastrophes presque partout (c'est aussi un terme exact qui signifie «partout, sauf pour un ensemble de mesures nulles»), et les états instables dans la nature sont rarement observés sans passer le «test du temps».

Si le couple se séparait «à cause de bêtises», elle était de toute façon destinée à se séparer, elle était instable. Les couples stables traversent des guerres et des famines, puis, parfois, ils se séparent, mais pas à cause de bagatelles, mais à la suite de changements profonds qui peuvent arriver à une personne au cours de sa vie. Dans la chaîne d'événements qui a conduit à l'accident de train, il n'est pas facile de distinguer un événement clé (une erreur spécifique ou un accident mortel) et, très probablement, la clé n'est pas un événement, mais une violation systématique des règles, conduisant le système à un état instable. S'il y a beaucoup de paramètres dans le système, et certains d'entre eux sont aléatoires, et notre vie est structurée de cette façon, alors les informations dans un tel système ont tendance à se perdre, et il ne sera pas possible de restaurer à quel moment exact de notre vie "tout s'est mal passé". Ne vous tourmentez pas avec des regrets sur ce qui s'est passé, mais regardez de plus près ce qui vous arrive maintenant, afin de ne pas manquer le vrai point de bifurcation.

À cet égard, nous pouvons rappeler l'une des lois de la merphologie, appelée la loi de restauration par un certain Dreisen:

Le temps d'amélioration de la situation est inversement proportionnel au temps de sa détérioration.

L'observation suivante est donnée à titre d'exemple: il faut plus de temps pour coller le vase que pour le casser. Cette loi décrit de manière surprenante avec précision la relation entre les taux caractéristiques du processus de relaxation d'un système stable, qui peut être décrite par une loi exponentielle décroissante $$$e ^ {- \ lambda t}$ et le taux de développement du processus catastrophique dans un système instable, dans l'approximation linéaire - la croissance exponentielle d'une petite perturbation $$$e ^ {\ lambda t}$ . Ces vitesses sont en effet inversement proportionnelles les unes aux autres. L'exemple de vase, cependant, n'est pas la relaxation - une transition vers l'état le plus probable. Il est plus proche d'un autre processus - de l' auto-organisation , ce processus, en première approximation, est décrit par la loi logistique et plus proche de la relaxation que du désastre.

Processus typiques non stationnaires: catastrophe, relaxation et auto-organisation, ayant le même temps caractéristique.

$$

$$* * *$$

Parfois, en marchant dans la neige, je suis surpris qu'un flocon de neige tombe sur mon nez. Je suis surpris que la probabilité de cet événement soit négligeable. À en juger par elle, elle est née haut dans le ciel au-dessus de l'océan Pacifique, encerclée par des courants turbulents irréguliers dans le nuage, est tombée en continu de changement de direction ... pour atteindre le bout de mon nez! Et quel chemin étonnant les photons ont-ils parcouru depuis une étoile lointaine!? Pendant des dizaines de milliers d'années, ils se sont précipités à travers l'Univers, ils n'ont pas été avalés par la poussière, ils n'ont pas rencontré d'astéroïde! Ils sont nés dans le monde quantique d'une étoile lointaine et ont terminé leur voyage dans le monde quantique de la protéine opsine sur la rétine de mon œil. Il n'y a aucun sens à considérer la probabilité de cet événement, il est nul, mais l'événement se produit, et je vois la lumière vacillante d'une étoile. Maintenant, il est clair que tout cela est dû au fait que la zone de mon nez et même les molécules ont une mesure non nulle, mais toujours incroyable: ce qui n'aurait certainement pas dû se produire se produit toujours!

Laissez les philosophes discuter du sort prédéterminé ou accidentel, de la vérité ou du fantôme de notre connaissance de la nature. J'exhorte le lecteur à regarder le monde du haut des abstractions mathématiques et à admirer sa beauté et sa cohérence.