Logique à trois valeurs
Liste des réalisations
- Portes logiques ternaires de base: T_NOT, T_OR, T_AND, T_NAND, T_NOR, T_XOR et plus
- Synthèse, minimisation et réalisation pour les fonctions ternaires
- Ternaire demi-additionneur, ternaire plein additionneur, ternaire ondulation porter additionneur
- Soustracteur ternaire complet, comparateur, multiplicateur, multiplexeur / démultiplexeur
- Tongs et loquets à rabat ternaire
- Une unité arithmétique et logique ternaire primitive (ALU)
Conventions et technologies utilisées
- Ternaire déséquilibré (0, 1, 2) a été utilisé dans la mise en œuvre
- 1 Trit est exprimé par 2 bits: 0 ~ 00, 1 ~ 01, 2 ~ 10 (11 n'est pas défini)
- ModelSim, Quartus prime, Logisim
Présentation
En tant qu'étudiants de première année de l'Université Innopolis, nous avons eu la possibilité de réaliser des projets tout au long de notre cours d'architecture informatique. Notre groupe était particulièrement intéressé par le système ternaire et son fonctionnement, nous avons donc décidé de mettre en place un système ternaire simple avec des composants de base (portes).
En logique, une logique à trois valeurs (également logique trinaire, trivalente, ternaire) est l'un des nombreux systèmes logiques à plusieurs valeurs dans lesquels il existe trois valeurs de vérité indiquant vrai, faux et une troisième valeur indéterminée.
La logique ternaire est compatible MVL (logique à valeurs multiples). Cependant, seuls trois états logiques sont utilisés, « 0 », « 1 » et « 2 ». On trouve que le radix optimal ( r ) d'un nombre fractionnaire est le logarithme naturel ( e ). La logique ternaire utilise la représentation numérique avec r = 3 , par rapport à la logique binaire qui utilise r = 2 , d'où le radix entier le plus économique qui est le plus proche du logarithme naturel e , est la base 3. Cette propriété spéciale de la base 3 a inspiré le premier ordinateur concepteurs pour construire un ordinateur ternaire.
Le premier ordinateur ternaire fonctionnel a été construit en Russie à l'Université d'État de Moscou en 1958. L'ordinateur a été conçu par Nikolay Brusentsov et ses collègues. Ils l'ont nommé Setun , comme la rivière qui coule près du campus universitaire.
Logique ternaire
Une fonction logique ternaire est un mappage F: {0,1,2} n -> {0,1,2} . Nous discuterons des avantages et des inconvénients de la logique ternaire par rapport à la logique binaire.
Lorsque la logique booléenne a 2 2 = 4 opérateurs unaires, l'ajout d'une troisième valeur dans la logique ternaire conduit à un total de 3 3 = 27 opérateurs distincts sur une seule valeur d'entrée. De même, lorsque la logique booléenne a 2 2 2 = 16 opérateurs binaires distincts (opérateurs avec 2 entrées), la logique ternaire a 3 3 2 = 19 683 de ces opérateurs. Lorsque nous pouvons facilement nommer une fraction significative des opérateurs booléens (pas, et, ou, nand, ni, exclusive ou, équivalence, implication), il est déraisonnable d'essayer de nommer tout sauf une petite fraction des opérateurs ternaires possibles.
Avantages de la logique ternaire
Une représentation logique ternaire permet un codage d'informations plus compact et efficace que la représentation logique binaire équivalente. L'argument énoncé est le suivant: si nous supposons qu'un circuit numérique a N combinaisons d'entrées possibles, alors un circuit binaire nécessite log 2 N lignes d'entrée et un circuit ternaire nécessite log 3 N lignes d'entrée.
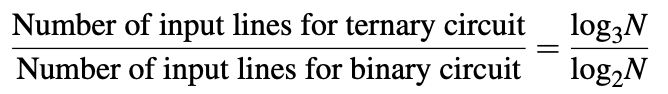

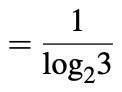

Par conséquent, une implémentation codée ternaire d'une fonction logique binaire donnée devrait nécessiter 0,63 fois les lignes d'entrée que l'implémentation binaire correspondante.
Inconvénients de la logique ternaire
Bien que les circuits logiques ternaires devraient nécessiter moins de lignes d'entrée que les circuits logiques binaires équivalents, les circuits logiques ternaires ne sont actuellement pas un choix pratique. Les raisons sont
- La technologie d'implémentation du matériel ternaire est toujours aux niveaux théorique, de simulation et de test en laboratoire
- La représentation de trois niveaux logiques ternaires (0, 1 et 2) à l'aide des niveaux de tension de la technologie existante n'est pas encore définie de manière efficace
- Aucun modèle de calcul et langage de programmation n'est développé. Cependant, la simulation des résultats de la mise en œuvre de circuits ternaires utilisant des semi-conducteurs à oxyde métallique complémentaire (CMOS), des diodes à effet tunnel résonnant (RTD) et des technologies de nanotubes de carbone, démontrant que la logique ternaire peut être un choix pour les futurs calculs.
Diverses représentations possibles du système ternaire
- Système numérique ternaire (ternaire déséquilibré) , chaque chiffre est un trit (chiffre trinaire) ayant une valeur de: 0, 1 ou 2
- Ternaire équilibré , chaque chiffre a l'une des 3 valeurs: -1, 0 ou +1; ces valeurs peuvent également être simplifiées à -, 0, +, respectivement (le plus couramment utilisé)
- Représentation binaire redondante , chaque chiffre peut avoir une valeur de -1, 0, 0/1 (la valeur 0/1 a deux représentations différentes)
- Système de nombres binaires de biais , seul le chiffre non nul le plus significatif a une valeur 2 et les chiffres restants ont une valeur de 0 ou 1
En savoir plus sur le système de numérotation ternaire équilibré
Aujourd'hui, presque tout le matériel est conçu pour l'informatique binaire. Si nous avions un composant électronique stable avec trois états stables, le monde se serait peut-être tourné vers l'informatique ternaire. Cependant, ce n'est pas la vérité aujourd'hui. La notation radix ternaire équilibrée a certaines propriétés bénéfiques:
- L'inversion ternaire est facile, il suffit d'échanger -1 avec 1 et vice versa. Si nous utilisons un exemple, 24 est représenté par 1T0 et -24 par T10 en notation ternaire équilibrée (T est simplement une notation pour -1). C'est plus simple que la règle du complément à deux en logique binaire.
- Le signe d'un nombre est donné par son «trit» non nul le plus significatif
- L'opération d'arrondi à l'entier le plus proche est identique à la troncature.
- L'addition et la soustraction sont essentiellement la même opération (c'est-à-dire que vous ajoutez simplement les chiffres en utilisant les règles d'addition des chiffres)
Exemples:
21 10 = 1T10 3 ; 296 10 = 11T00T 3 ;
-24 10 = T10 3 ; -137 10 = T110T1 3
Arithmétique ternaire
L'arithmétique ternaire peut offrir une notation plus compacte que l'arithmétique binaire, et aurait été un choix évident si les fabricants de matériel avaient trouvé un commutateur ternaire.
Addition et multiplication ternaires équilibrées
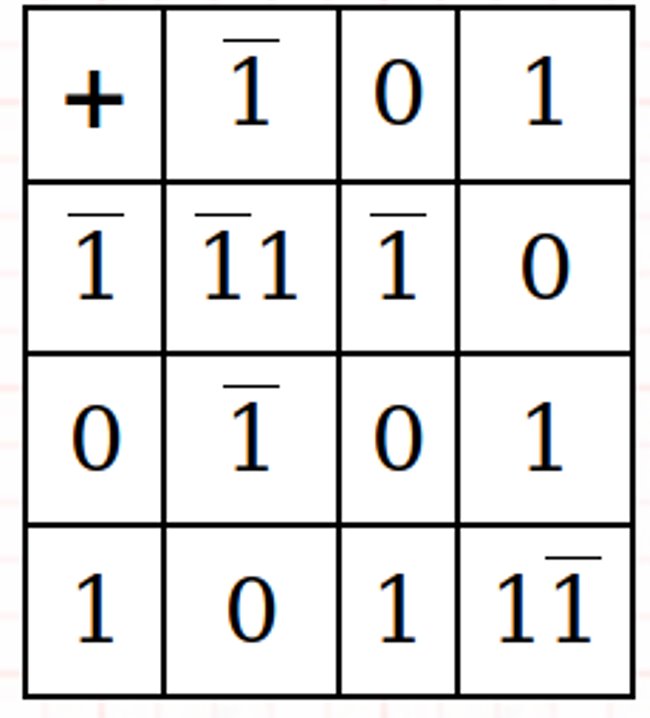
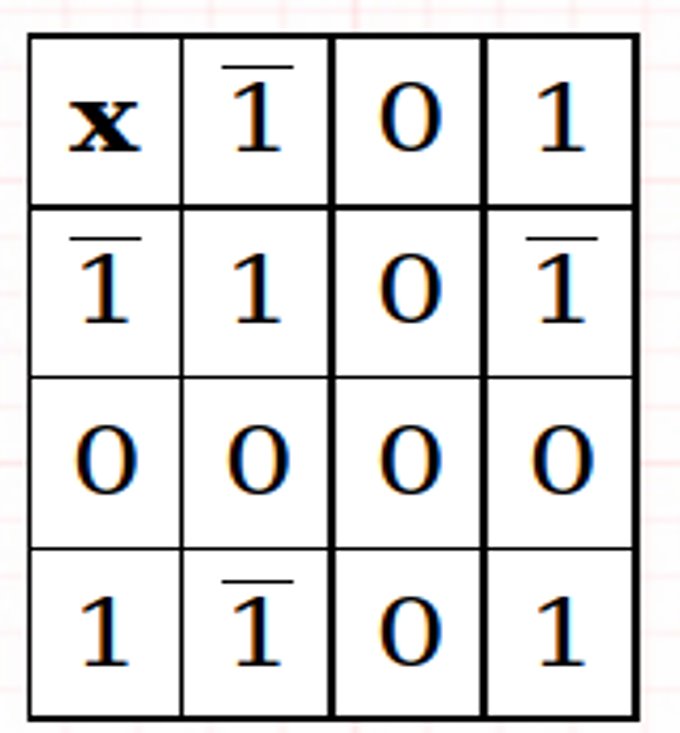
Exemples:
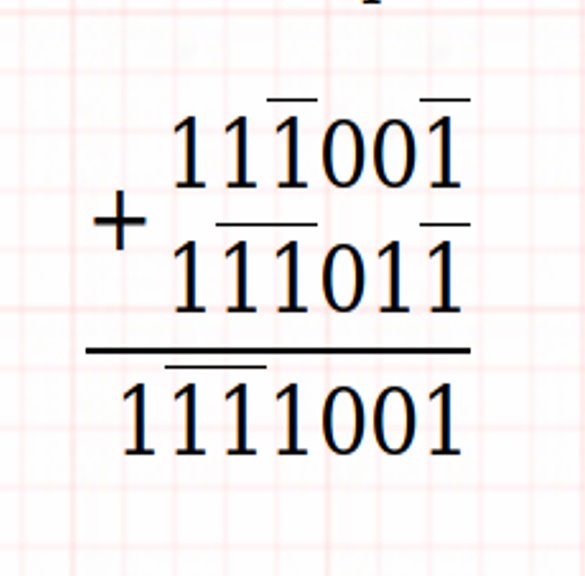
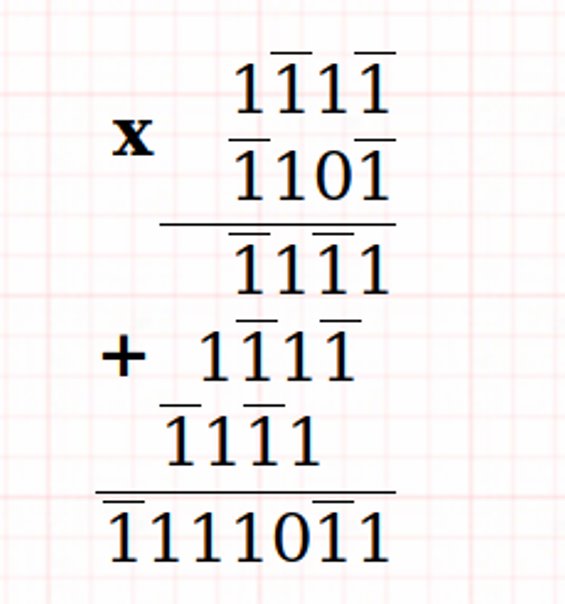
Circuits combinatoires ternaires (portes ternaires)
Un circuit combinatoire se compose de variables d'entrée, de portes logiques ternaires et de variables de sortie. La sortie du circuit ne dépend que de l'entrée actuelle. Les portes logiques acceptent les signaux des variables d'entrée et génèrent des signaux de sortie. Ce processus transforme les informations ternaires de
les données d'entrée données aux données de sortie ternaires requises.
Comme mentionné ci-dessus, nous pouvons facilement nommer une fraction significative des opérateurs booléens (pas, et, ou, nand, ni, exclusive ou, équivalence, implication), cependant, il est déraisonnable d'essayer de nommer tout sauf une petite fraction du possible opérateurs ternaires. Nous considérerons les circuits ternaires suivants:
Et (Min) : Il est naturel d'étendre le booléen et la fonction à une fonction ternaire en déclarant que le résultat est vrai uniquement si les deux entrées sont vraies, faux si une entrée est fausse et inconnu sinon.
Et circuit / table de vérité Ou (Max) : Il est également naturel d'étendre le booléen ou la fonction au ternaire en déclarant que le résultat est vrai si une entrée est vraie, faux uniquement si les deux entrées sont fausses et inconnu sinon.
Ou circuit / table de vérité Consensus : dans la logique booléenne, l'inverse de exclusif ou est vrai lorsque les deux entrées sont identiques et faux lorsqu'elles sont différentes. Il existe plusieurs extensions naturelles de cette idée à la logique ternaire. L'un d'eux est le consensus logique d'un ensemble de variables, qui est vrai si tous sont vrais, faux si tous sont faux et autrement inconnu
Circuit de consensus / table de vérité N'importe quel : lorsqu'un consensus exige que les deux entrées soient d'accord avant d'affirmer autre chose qu'inconnu, l'opérateur d'accepter n'importe quoi ne déclare une conclusion inconnue que si les deux entrées sont inconnues ou en désaccord actif. Sinon, il saute à une conclusion à partir de toute entrée non inconnue à sa disposition.
Tout circuit / table de vérité Incrémentation et décrémentation : dans la logique booléenne, l'onduleur peut être considéré comme incrémentant ou décrémentant son argument modulo 2. Logique interne, les fonctions d'incrémentation et de décrémentation modulo 3 sont assez distinctes de l'inversion.
Circuit d'incrémentation et de décrémentation Synthèse, minimisation et réalisation pour les fonctions ternaires
Relations interreliées dans le système logique ternaire
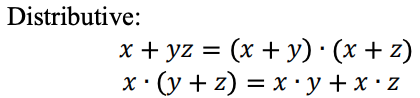
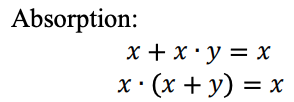
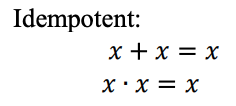
Une fonction logique ternaire peut être représentée comme une expression Max-Min. Les expressions ternaires Max-Min sont définies comme suit:
Variable : Tout symbole qui prend la valeur de l'ensemble T ∈ {0,1,2} est une variable ternaire.
Littéral : les littéraux sont des formes transformées d'une variable. Ils sont utilisés pour former des expressions Max-Min.
Dans la littérature, deux types de littéraux sont couramment utilisés: les post-littéraux à 1 réduction et les post-littéraux à 2 réductions. Un Post-littéral réduit d'une variable x est représenté par x i , où i ∈ {0,1,2}. Lorsque x = i, alors x i = 1, sinon x i = 0. Les littéraux de poste 1 réduits d'une variable sont indiqués ci-dessous.
Un post-littéral réduit de 2 d'une variable x est représenté par x i , où i ∈ {0,1,2}. Lorsque x = i, alors x i = 2, sinon x i = 0. Les post-littéraux réduits d'une variable sont indiqués ci-dessous. Cet exemple utilise différents ensembles de littéraux pour former des expressions Max-Min comme discuté précédemment.
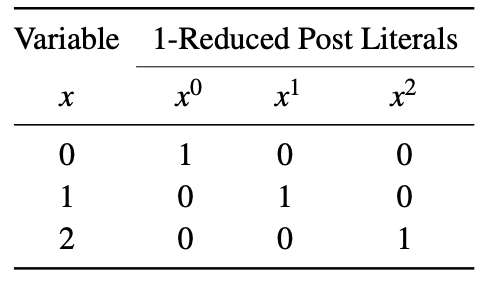
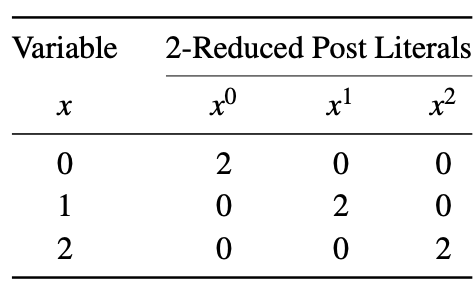
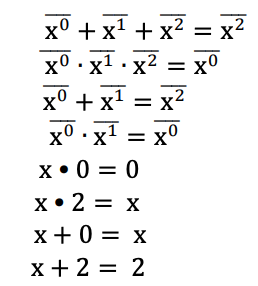
Minterm : lorsque des littéraux de variables d'une fonction sont combinés à l'aide de l'opération Min, le terme est appelé minterm. Par exemple, pour une fonction logique ternaire à 3 variables F (x, y, z), xyz et xz sont deux exemples de termes.
Expression Max-Min : Lorsque deux ou plusieurs minterms sont combinés à l'aide d'opérations Max, l'expression est appelée expression Max of minterms (Max-Min). Par exemple, pour une fonction logique ternaire à 3 variables, F (x, y, z) = xy + yz + xyz est un exemple d'expression Max-Min.
Toute fonction F (x, y, z) peut toujours être représentée comme
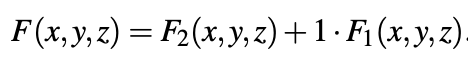
Trois méthodes de base pour minimiser les fonctions ternaires sont:
- Manipulation de l'expression de l'algèbre comme dans l'algèbre booléenne.
- La méthode tabulaire.
- Méthode de la carte Ternary K.
Pour la mise en œuvre de circuits ternaires, il est nécessaire de convertir la variable ternaire en variable unaire (à l'aide du tableau 2-Reduced Post Literals).
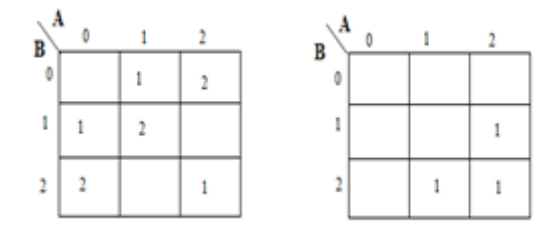
Demi-additionneur ternaire
Un circuit pour l'addition de deux nombres 1 trit est appelé demi-additionneur. le circuit ne considère pas un report généré dans l'addition précédente. Le processus d'addition dans le système logique ternaire est illustré ci-dessous. Ici A et B sont deux entrées et additionnent (S) et portent (CARRY)
sont deux sorties.
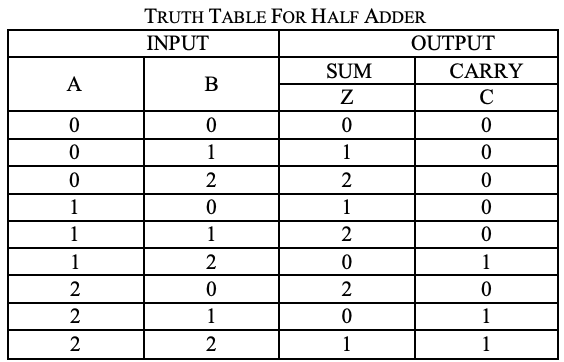
Analyse
Une carte karnaugh (K-map) est utilisée pour représenter la somme et la sortie de sortie. Les K-maps sont utiles pour minimiser et optimiser les circuits logiques. Ici, une K-map de 2 entrées est utilisée. Puisqu'aucun regroupement de 2 et 1 n'est possible, l'équation de sortie est comme ci-dessous.
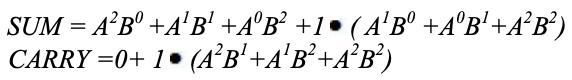
Implémentation
Circuit demi-additionneur ternaire / Verilogmodule half_adder ( input [1:0] A, [1:0] B, output [1:0] sum, [1:0] carry ); wire [1:0] temp = 2'b01; wire [1:0] a0, a1, a2, b0, b1, b2; wire [1:0] i0, i1, i2, i3, i4, i5; wire [1:0] o0, o1, o2, o3, o4; wire [1:0] c0, c1, c2, c3; mask msk_1(A, a0, a1, a2); mask msk_2(B, b0, b1, b2); andgate and_1(a2,b0,i0); andgate and_2(a1,b1,i1); andgate and_3(a0,b2,i2); // partial products orgate or_1(i0, i1, o0); orgate or_2(o0, i2, o1); // f1 andgate and_4(a1,b0,i3); andgate and_5(a0,b1,i4); andgate and_6(a2,b2,i5); // partial products orgate or_3(i3, i4, o2); orgate or_4(o2, i5, o3); // f2 andgate and_7(o3,temp,o4); // 1.f2 andgate andc_0(a2,b1,c0); andgate andc_1(a1,b2,c1); orgate orc_0(c0,c1,c2); orgate orc_1(c2,i5,c3); andgate andc_2(c3,temp,carry); // carry orgate or_5(o1, o4, sum); // sum endmodule
Additionneur complet ternaire
Comme pour les demi-additionneurs, une étape d'un additionneur ternaire complet peut être décrite par un tableau numérique donnant la somme SUM et effectue CARRY en fonction des trois entrées A, B, ainsi que le report en C :
Analyse
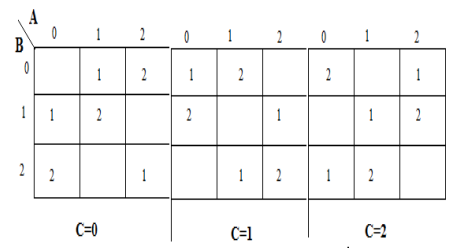
Une carte karnaugh (K-map) est utilisée pour représenter la somme et la sortie de sortie. Les K-maps sont utiles pour minimiser et optimiser les circuits logiques. Ici, une K-map de 3 entrées est utilisée.
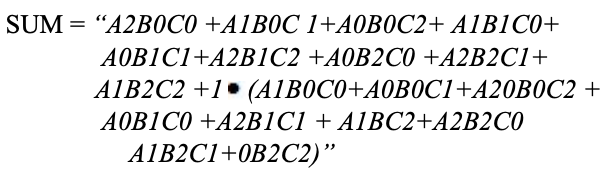
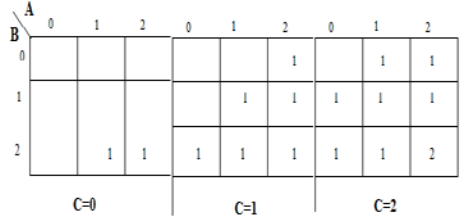
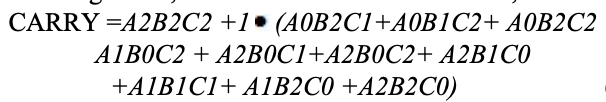
Implémentation
Circuit additionneur ternaire complet / verilog module ternary_full_adder ( input [1:0] A, [1:0] B, [1:0] c_in, output [1:0] sum, [1:0] c_out ); wire [1:0] temp1 = 2'b01; wire [1:0] temp2 = 2'b00; wire [1:0] a0, a1, a2, b0, b1, b2, a20; wire [1:0] i0, i1, i2, i3, i4; wire [1:0] i5, i6, i7, i8, i9, i10, i11, i12, i13, i14, i15, i16, i17; wire [1:0] o0, o1, o2, o3, o4, o5, o6, o7, o8, o9; wire [1:0] c0, c1, c2; wire [1:0] h0, h1, h2, h3, h4, h5, h6, h7; wire [1:0] t0, t1, t2, t3, t4, t5, t6, t7, t8, t9, t10, t11, t12, t13, t14, t15, t16; wire [1:0] g0, g1, g2, g3, g4, g5, g6, g7, g8, g9, g10, g11, g12, g13, g14, g15; mask mk_1(A, a0, a1, a2); mask mk_2(B, b0, b1, b2); mask mk_3(c_in, c0, c1, c2); andgate3 and3_1(a2,b0,c0, i0); andgate3 and3_2(a1,b0,c1, i1); andgate3 and3_3(a0,b0,c2, i2); andgate3 and3_4(a1,b1,c0, i3); andgate3 and3_5(a0,b1,c1, i4); andgate3 and3_6(a2,b1,c2, i5); andgate3 and3_7(a0,b2,c0, i6); andgate3 and3_8(a2,b2,c1, i7); andgate3 and3_9(a1,b2,c2, i8); andgate3 and3_10(a1,b0,c0, i9); andgate3 and3_11(a0,b0,c1, i10); orgate or__(a2, a0, a20); andgate3 and3_12(a20,b0,c2, i11); // note a20 andgate3 and3_13(a0,b1,c0, i12); andgate3 and3_14(a2,b1,c1, i13); andgate3 and3_15(a1,B,c2, i14); andgate3 and3_16(a2,b2,c0, i15); andgate3 and3_17(a1,b2,c1, i16); andgate3 and3_18(temp2,b2,c2, i17); orgate or_1(i9, i10, o0); orgate or_2(o0, i11, o1); orgate or_3(o1, i12, o2); orgate or_4(o2, i13, o3); orgate or_5(o3, i14, o4); orgate or_6(o4, i15, o5); orgate or_7(o5, i16, o6); orgate or_8(o6, i17, o7); andgate and_1(o7, temp1, o8); // 1.f2 orgate or_9(i0, i1, h0); orgate or_10(h0, i2, h1); orgate or_11(h1, i3, h2); orgate or_12(h2, i4, h3); orgate or_13(h3, i5, h4); orgate or_14(h4, i6, h5); orgate or_15(h5, i7, h6); orgate or_16(h6, i8, h7); orgate or_17_(h7, o8, sum); // sum // carry andgate3 and3_19(a2,b2,c2, t0); // f1 andgate3 and3_20(a0,b1,c2, t1); andgate3 and3_21(a0,b2,c2, t2); andgate3 and3_22(a0,b2,c1, t3); andgate3 and3_23(a1,b2,c0, t4); andgate3 and3_24(a2,b2,c0, t5); andgate3 and3_25(a1,b1,c1, t6); andgate3 and3_26(a1,b2,c1, t7); andgate3 and3_27(a1,b0,c2, t8); andgate3 and3_28(a1,b1,c2, t9); andgate3 and3_29(a1,b2,c2, t10); andgate3 and3_25_(a2,b0,c2, t11); andgate3 and3_26_(a2,b1,c2, t12); andgate3 and3_27_(a2,b0,c1, t13); andgate3 and3_28_(a2,b1,c1, t14); andgate3 and3_29_(a2,b2,c1, t15); andgate3 and3_9_(a2,b1,c0, t16); orgate or_17(t1, t2, g0); orgate or_18(g0, t3, g1); orgate or_19(g1, t4, g2); orgate or_20(g2, t5, g3); orgate or_21(g3, t6, g4); orgate or_22(g4, t7, g5); orgate or_23(g5, t8, g6); orgate or_24(g6, t9, g7); orgate or_25(g7, t10, g8); orgate or_21_(g8, t11, g9); orgate or_22_(g9, t12, g10); orgate or_23_(g10, t13, g11); orgate or_24_(g11, t14, g12); orgate or_25_(g12, t15, g13); orgate or_5_(g13, t16, g14); //f2 andgate and_2(g14, temp1, g15); // 1.f2 orgate or_26(g15, t0, c_out); // carry endmodule
Soustracteur ternaire complet
Ternary full-Subtractor est un circuit qui soustrait deux entrées et emprunts précédents. La table de vérité pour Subtractor est présentée ci-dessous

Analyse et mise en œuvre du soustracteur complet ternaire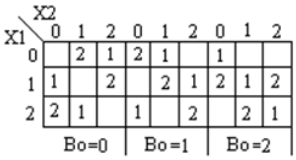
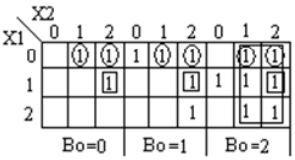
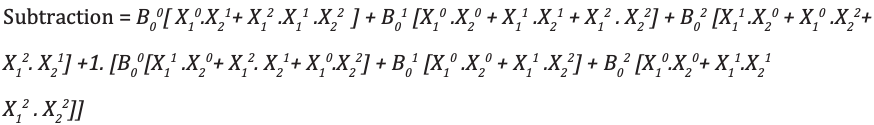
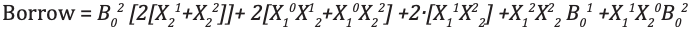
Code module full_subtractor( input [1:0] P, Q, b_in, output [1:0] diff, b_out ); wire [1:0] temp1 = 2'b01; wire [1:0] temp2 = 2'b10; wire [1:0] a0, a1, a2, b0, b1, b2; wire [1:0] i0, i1, i2, i3, i4, i5, i6, i7, i8, i9, i10, i11, i12, i13, i14, i15, i16, i17; wire [1:0] c0, c1, c2, c3; wire [1:0] h0, h1, h2, h3, h4, h5, h6, h7, h8, h9, h10, h11; wire [1:0] t0, t1, t2, t3, t4, t5, t6, t7, t8, t9; wire [1:0] p0, p1, p2; wire [1:0] q0, q1, q2; mask mk_1(P, p0, p1, p2); mask mk_2(Q, q0, q1, q2); mask mk_3(b_in, b0, b1, b2); andgate and_0(p0, q1, i0); andgate3 and3_0(p2, p1, q2, i1); orgate or_0(i0, i1, i2); andgate and_1(b0, i2, i3); // first expression andgate and_2(p0, q0, i4); andgate and_3(p1, q1, i5); andgate and_4(p2, q2, i6); orgate or_1(i4, i5, i7); orgate or_2(i7, i6, i8); andgate and_5(i8, b1, i9); // second expression andgate and_6(p1, q0, i10); andgate and_7(p0, q2, i11); andgate and_8(p2, q1, i12); orgate or_3(i10, i11, i13); orgate or_4(i13, i12, i14); andgate and_9(i14, b2, i15); // third expression orgate or_5(i3, i9, i16); orgate or_6(i16, i15, c0); //f1 orgate or_7(i10, i12, t0); orgate or_8(t0, i11, t1); andgate and_10(t1, b0, t2); // 1 expression andgate and_11(p1, q2, i17); orgate or_9(i4, i17, t3); andgate and_12(t3, b1, t4); // 1- expression orgate or_10(i4, i5, t5); orgate or_11(t5, i6, t6); andgate and_12_(t6, b2, t7); // 1-- expression orgate or_12(t2, t4, t8); orgate or_13(t8, t7, t9); andgate and_13(t9, temp1, c1); orgate or_14(c0, c1, diff); // difference orgate or_15(q1, q2, h0); andgate and_14(h0, temp2, h1); andgate and_15(h1, b2, h3); // 1 b orgate or_16(i0, i11, h4); andgate and_16(h4, temp2, h5); // 1- b andgate and_17(i17, temp2, h6); // 1-- b andgate3 and3_1(p2, q2, b1, h7); // 1--- b andgate3 and3_2(p1, q0, b2, h8); // 1---- b orgate or_17(h3, h5, h9); orgate or_18(h9, h6, h10); orgate or_19(h10, h7, h11); orgate or_20(h11, h8, b_out); // borrow endmodule
Additionneur de portage d'ondulation ternaire
L'additionneur de report d'ondulation (RCA) est un circuit bien connu pour effectuer l'addition de deux nombres en cascadant des additionneurs ternaires complets. Un RCA ternaire est assez similaire à son homologue binaire. Un demi-additionneur ternaire est utilisé pour ajouter les chiffres ternaires les moins significatifs. Les autres sont résumés par Ternary Full Adders. Comme mentionné précédemment, Ternary Full Adder ajoute trois variables d'entrée ternaires.
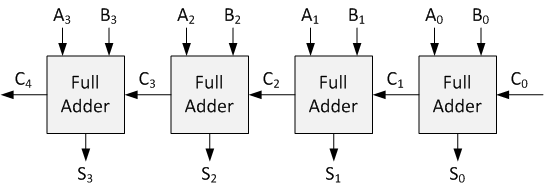
Implémentation
code verilog: additionneur de report d'ondulation ternaire module ternary_ripple_adder ( input [15:0] input1 , input [15:0] input2 , output [15:0] out , output [1:0] overflow_trit ); wire [15:0] carry ; reg tem; assign carry[0] = tem; assign carry[1] = tem; always @(input1, input2) begin tem <= 1'b0; end generate genvar i; for (i = 0; i <= 12; i=i+2) begin full_add af({input1[i+1],input1[i]}, {input2[i+1],input2[i]}, {carry[i+1],carry[i]}, {out[i+1], out[i]}, {carry[i+3],carry[i+2]}); end full_add af({input1[15],input1[14]}, {input2[15],input2[14]}, {carry[15],carry[14]}, {out[15], out[14]}, overflow_trit); endgenerate endmodule
Comparateurs ternaires
Le circuit de comparaison ternaire campe deux entrées X 1 , X 2 et génère en conséquence une sortie comme X 1 = X 2 , X 1 > X 2 , X 1 <X 2 . La table de vérité pour un comparateur ternaire est présentée ci-dessous
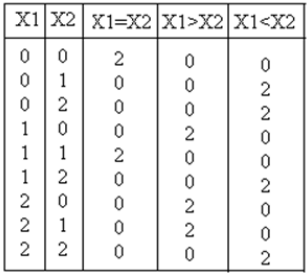
Analyse et mise en œuvreL'équation de sortie pour X 1 = X 2 , X 1 > X 2 , X 1 <X 2 sont:
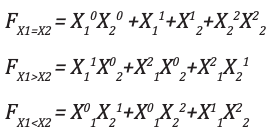
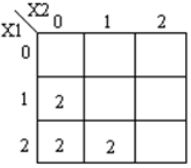
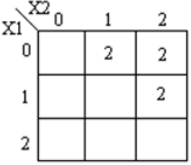
Les k-maps correspondantes sont indiquées ci-dessous

Code module ternary_comparators ( input [1:0] x1, x2, output [1:0] f1, f2, f3 ); wire [1:0] t0, t1, t2, t3, t4, t5, t6, t7; wire [1:0] h0, h1, h2, h3, h4, h5; wire [1:0] x10, x11, x12; wire [1:0] x20, x21, x22; mask mk_1(x1, x10, x11, x12); mask mk_2(x2, x20, x21, x22); andgate and_0(x10, x20, t0); andgate and_1(x22, x22, t1); orgate or_0(t0, t1, h0); orgate or_1(h0, x11, h1); orgate or_2(h1, x21, f1); // x1 == x2 andgate and_2(x11, x20, t2); andgate and_3(x12, x20, t3); andgate and_4(x12, x21, t4); orgate or_3(t2, t3, h3); orgate or_4(h3, t4, f2); // x1>x2 andgate and_5(x10, x21, t5); andgate and_6(x10, x22, t6); andgate and_7(x11, x22, t7); orgate or_5(t5, t6, h4); orgate or_6(h4, t7, f3); // x1<X2 endmodule
Multiplicateur ternaire
Le multiplicateur ternaire est un circuit qui multiplie deux nombres d'entrée et génère le produit correspondant. La table de vérité pour ce circuit est présentée ci-dessous:
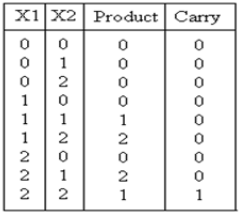
Analyse et mise en œuvreL'expression résultante pour le produit et le transport est indiquée:
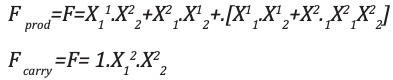
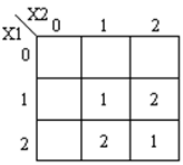
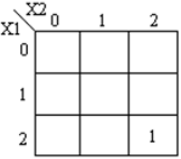
Les K-maps correspondantes sont affichées:
Code module ternary_multiplier ( input [1:0] A, [1:0] B, output [1:0] product, [1:0] carry ); wire [1:0] temp = 2'b01; wire [1:0] a0, a1, a2, b0, b1, b2; wire [1:0] i0, i1, i2, i3, i4, i5; wire [1:0] o0, o1, o2, o3, o4; mask msk_1(A, a0, a1, a2); mask msk_2(B, b0, b1, b2); andgate and_1(a1,b2,i0); andgate and_2(a2,b1,i1); orgate or_1(i0, i1, o0); // f1 andgate and_4(a1,b1,i3); andgate and_5(a2,b2,i4); orgate or_3(i3, i4, o2); andgate and_3(temp,o2,o3); orgate or_4(o3, o0, product); // product andgate andc_0(a2,b2,o4); andgate andc_1(temp,o4,carry); // carry endmodule
Multiplexeurs et démultiplexeurs ternaires
Le multiplexeur est un circuit ayant plusieurs entrées et une seule sortie. Il est également appelé décodeur. La fonction de sortie du multiplexeur est déterminée par le nombre de lignes de fonction. Ainsi pour 2 trit
multiplexeur la sortie sera 3 2 = 9 et deux seront les lignes de sélection de fonction. Multiplexeur ie fonction
la logique de sélection sélectionne 1 fonction sur 9 en sortie. La logique de sélection de fonction est implémentée à l'aide de portes logiques. L'équation de sortie de la logique de sélection de fonction est:
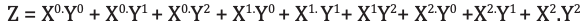
Analyse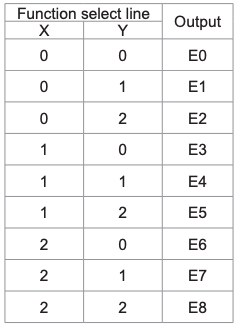
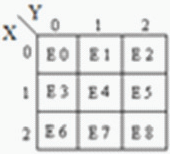
Le démultiplexeur est également appelé codeur. Sa fonctionnalité est inverse de celle du multiplexeur. Il accepte l'entrée unique et la distribue sur plusieurs sorties
Verrou ternaire simple
Bien que la conception de circuits mettant en œuvre une logique ternaire combinatoire soit simple, la conception d'un élément de mémoire ternaire simple et robuste (c.-à-d. Verrou) adapté à la mise en œuvre de circuits intégrés (CI) a été difficile. Cependant, un verrou ternaire simple peut être obtenu en remplaçant les portes binaires NOR ou NAND utilisées par des portes ternaires T_NOR ou T_NAND correspondantes.
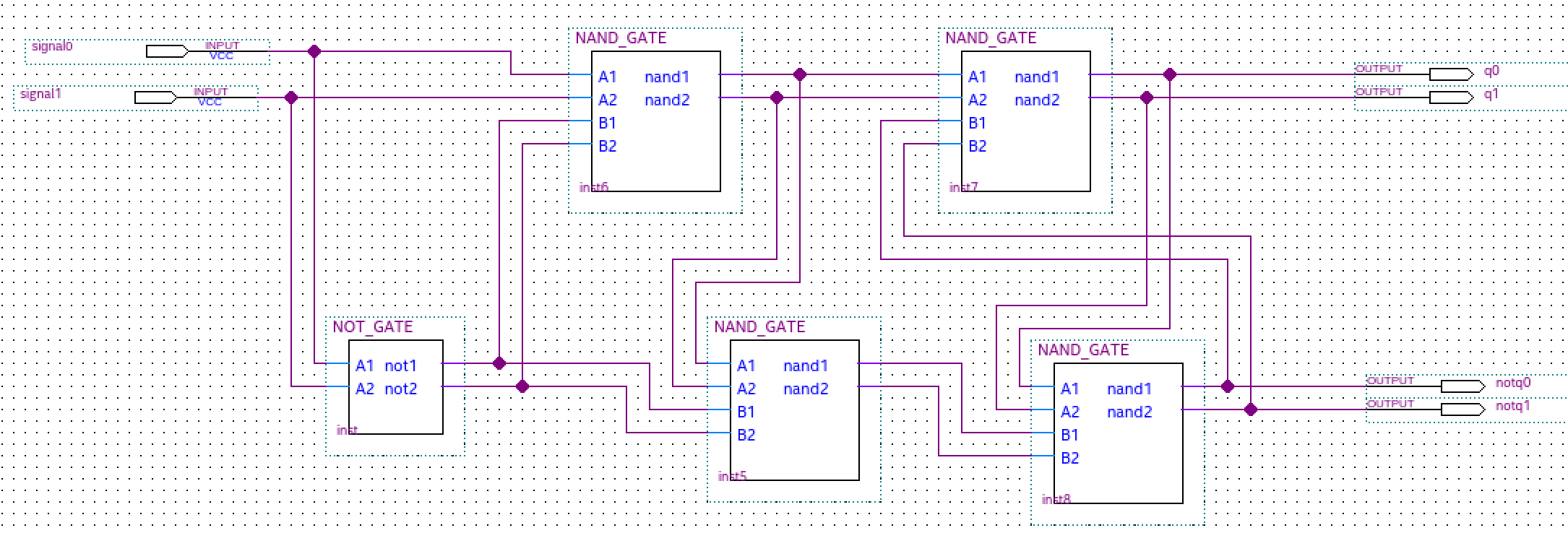
Bascule simple ternaire D
Le Flip Slap-Flop (FFF) ternaire D maître esclave (MS) est réalisé sur la base des verrous ternaires D. Ceci est similaire à la façon dont la bascule D binaire (FF) est réalisée à l'aide de verrous D binaires. Le diagramme logique et la description du fonctionnement de la bascule binaire D MS sont bien connus. Afin de mettre en œuvre le MS ternaire D FFF , nous remplaçons les verrous binaires D par des verrous ternaires D (réalisés avec des portes minimales négatives ternaires à deux entrées - NAND) et les onduleurs binaires avec des onduleurs ternaires simples (STI). Les tables de vérité pour les circuits NAND ternaires et les circuits STI ternaires sont affichées
Table de vérité pour les circuits nand et sti Pour MS ternaire D FFF avec horloge binaire, les données sont ternaires (logique 0, 1 et 2) et l'horloge est binaire (basse et haute - dans notre
implémentation, logique 0 et 2). Le MS ternaire D FFF avec
horloge binaire peut lire les données lorsque l'horloge passe de faible à
haut (bord positif) ou de haut à bas (bord négatif), selon
sur le nombre d'IST.
Les entrées du ternaire D FFF sont Data et Clk, et les sorties sont Q et Not_Q. Le signal d'horloge est binaire et les niveaux logiques sont notés 0 et 2, afin de maintenir la correspondance avec l'implémentation électrique
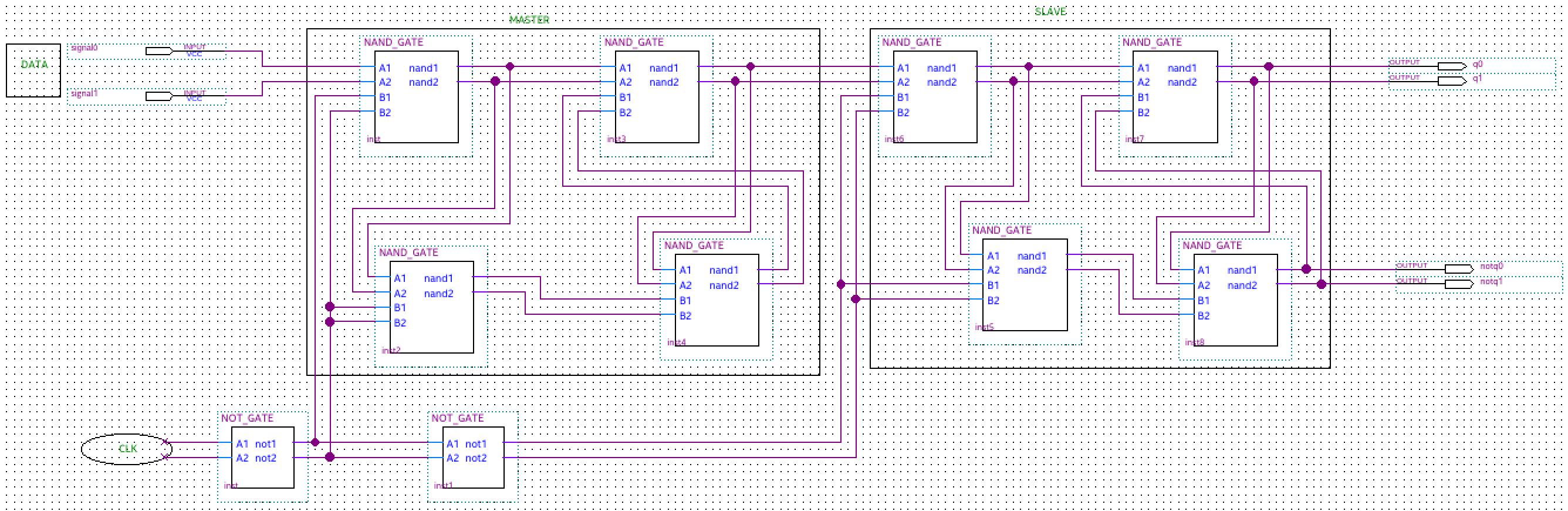
Unité arithmétique et logique ternaire 1 bit (T-ALU)
L'unité logique arithmétique ternaire (ALU) est un circuit numérique utilisé pour effectuer des opérations arithmétiques et logiques. Il représente l'élément constitutif fondamental de l'unité centrale de traitement (CPU) d'un ordinateur ternaire. ALU effectue des opérations arithmétiques comme l'addition, la soustraction, la multiplication et les opérations logiques de comparaison, NAND, NOR, NOT, AND et OR. Ci-dessous est montrée une architecture primitive d'un ALU 1 trit
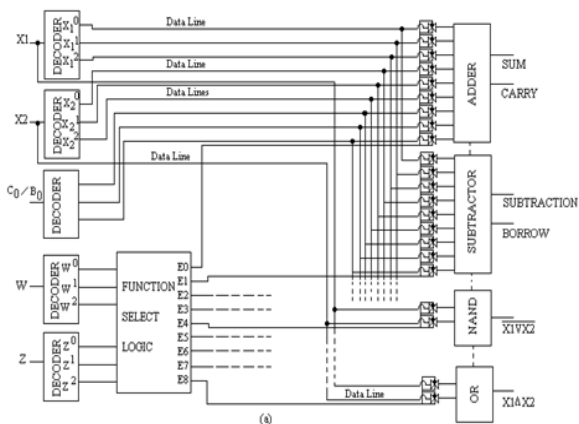
Table de vérité et fonctionnement pour T-ALU Les blocs de construction de base de l'ALU sont les décodeurs, la logique de sélection de fonction (multiplexeur), la porte de transmission et les modules de traitement séparés. La logique de sélection de fonction sélectionne 1 des 9 fonctions répertoriées en fonction de l'état logique sur les lignes de sélection de fonction W et Z.
Les lignes de sortie de la logique de sélection sont connectées à TG (porte ternaire) associée à chaque module. Tout module est sélectionné uniquement lorsque le TG associé est activé, sinon il est isolé des lignes de données. Par exemple, si l'entrée des lignes de sélection W et Z = 0, la sortie E 0 de la logique de sélection est élevée (2) tandis que E 1 , à E 8 est faible (0), donc TG associé au module additionneur sera autorisé à autoriser les données
lignes à connecter aux modules additionneurs tandis que les autres modules sont isolés des lignes de données.
Enfin, en cascadant n / 2 tranches de trit ALU, une n trit ALU peut être formée.