Besoin de plus de flous différents

Le flou d'image avec le filtre Flou gaussien est largement utilisé dans une grande variété de tâches. Mais parfois, vous voulez un peu plus de variété qu'un seul filtre pour toutes les occasions, dans lequel un seul paramètre se prête au réglage - sa taille. Dans cet article, nous examinerons plusieurs autres implémentations de flou.

Présentation

L'effet Flou gaussien est une opération linéaire et représente mathématiquement une convolution de l'image avec la matrice de filtre. Dans ce cas, chaque pixel de l'image est remplacé par la somme des pixels proches prise avec certains facteurs de pondération.

Le filtre est appelé gaussien car il est construit à partir d'une fonction appelée gaussienne, $$$e ^ {- x ^ 2}$:



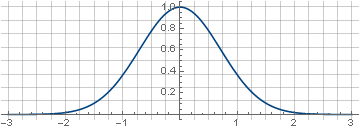
dont une version bidimensionnelle est obtenue par sa rotation autour de l'axe des ordonnées, $$$e ^ {- (x ^ 2 + y ^ 2)}$:



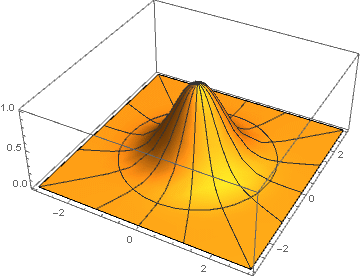
Ici pour chaque paire de coordonnées $$$(x, y)$la distance au centre est calculée par la formule $$$\ sqrt {x ^ 2 + y ^ 2}$, qui est passé comme argument à la fonction gaussienne - et, comme vous pouvez facilement le voir, $$$e ^ {- \ left (\ sqrt {x ^ 2 + y ^ 2} \ right) ^ 2}$réduit à $$$e ^ {- (x ^ 2 + y ^ 2)}$.

Matrice construite sur un segment $$$[- 3,3]$et avec un certain niveau d'échantillonnage, cela ressemblera à ceci:

$$

$$\ left (\ begin {array} {ccccccc} 1,52 \ fois 10 ^ {- 8} & 2,26 \ fois 10 ^ {- 6} & 0,0000454 & 0,000123 & 0,0000454 & 2,26 \ fois 10 ^ {- 6} & 1,52 \ fois 10 ^ {- 8} \\ 2,26 \ fois 10 ^ {- 6} & 0,000335 & 0,00674 & 0,0183 & 0,00674 & 0,000335 & 2,26 \ fois 10 ^ {- 6} \\ 0,0000454 & 0,00674 & 0,135 & 0,368 & 0,135 & 0,00674 & 0,0000454 \\ 0,000123 & 0,0183 & 0,368 & 1,00 & 0,368 & 0,0183 & 0,000123 \\ 0,0000454 & 0,00674 & 0,135 & 0,368 & 0,135 & 0,00674 & 0,0000454 \\ 2,26 \ fois 10 ^ {- 6} & 0,000335 & 0,00674 & 0,0183 & 0,00674 & 0,000335 & 2,26 \ fois 10 ^ {- 6} \\ 1,52 \ fois 10 ^ {- 8} & 2,26 \ fois 10 ^ {- 6} & 0,0000454 & 0,000123 & 0,0000454 & 2,26 \ fois 10 ^ {{ -6} & 1,52 \ fois 10 ^ {- 8} \\ \ end {array} \ right)$$

Ou, si nous considérons les valeurs des éléments de la matrice comme un niveau de luminosité, comme ceci:



En termes de traitement du signal, cela s'appelle la réponse impulsionnelle, car c'est exactement ce à quoi ressemblera le résultat de la convolution de ce filtre avec une seule impulsion (dans ce cas, un pixel).

Initialement, un gaussien est défini sur un intervalle infini. Mais du fait qu'il se désintègre assez rapidement, il est possible d'exclure des calculs des valeurs proches de zéro - car elles n'affecteront toujours pas le résultat. Dans les applications réelles, la normalisation de la valeur est également nécessaire pour qu'après convolution la luminosité de l'image ne change pas; et dans le cas de flou d'une image dans laquelle chaque pixel a la même couleur, l'image elle-même ne devrait pas changer.

Pour plus de commodité, la normalisation est également souvent utilisée en coordonnées, en introduisant un paramètre supplémentaire $$$\ sigma$(lu comme "sigma") - pour considérer un argument dans la plage $$$[- 1,1]$et $$$\ sigma$détermine le taux de compression du gaussien:

$$

$$\ frac {e ^ {- \ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}}} {2 \ pi \ sigma ^ 2}$$

Séparateur de normalisation $$$2 \ pi \ sigma ^ 2$obtenu ici analytiquement par une intégrale définie à l'infini:

$$

$$\ int _ {- \ infty} ^ {\ infty} \ int _ {- \ infty} ^ {\ infty} e ^ {- \ frac {x ^ 2 + y ^ 2} {2 \ sigma ^ 2}} \ \, dx dy = 2 \ pi \ sigma ^ 2$$

Du fait que l'égalité tient $$$e ^ {- \ left (x ^ 2 + y ^ 2 \ right)} = e ^ {- x ^ 2} e ^ {- y ^ 2}$Le flou gaussien peut être implémenté séquentiellement, d'abord en lignes puis en colonnes - ce qui vous permet d'économiser beaucoup sur les calculs. Dans ce cas, il est nécessaire d'utiliser la formule de normalisation pour le cas unidimensionnel -

$$

$$\ frac {e ^ {- \ frac {x ^ 2} {2 \ sigma ^ 2}}} {\ sqrt {2 \ pi \ sigma ^ 2}}$$

Commencer

Pour un filtre arbitraire, nous devons d'abord définir notre propre fonction d'atténuation à partir d'une variable $$$f$, à partir de laquelle la fonction de deux variables est obtenue par rotation en remplaçant $$$x$sur $$$\ sqrt {x ^ 2 + y ^ 2}$où $$$x$et $$$y$ce sont les coordonnées de l'élément de matrice dans la plage $$$(- 1,1)$, et qui est ensuite utilisé pour remplir les éléments de la matrice. La normalisation ne sera pas considérée analytiquement, mais une sommation directe de tous les éléments de la matrice - c'est à la fois plus simple et plus précis - car après discrétisation la fonction est «amincie» et la valeur de normalisation dépendra du niveau de discrétisation.

Dans le cas où les éléments de la matrice sont numérotés à partir de zéro, les coordonnées $$$x$ou $$$y$est calculé par la formule

$$

$$\ frac {2 index} {size-1} -1$$

où $$$index$- le numéro de série de l'élément dans la ligne ou la colonne, et $$$taille$- nombre total d'éléments.

Par exemple, pour une matrice 5 par 5, cela ressemblerait à ceci:

$$

$$\ left (\ begin {array} {ccccc} f (-1, -1) & f \ left (- \ frac {1} {2}, - 1 \ right) & f (0, -1) & f \ left (\ frac {1} {2}, - 1 \ right) & f (1, -1) \\ f \ left (-1, - \ frac {1} {2} \ right) & f \ left (- \ frac {1} {2}, - \ frac {1} {2} \ droite) & f \ left (0, - \ frac {1} {2} \ right) & f \ left (\ frac { 1} {2}, - \ frac {1} {2} \ right) & f \ left (1, - \ frac {1} {2} \ right) \\ f (-1.0) & f \ left (- \ frac {1} {2}, 0 \ droite) & f (0,0) & f \ gauche (\ frac {1} {2}, 0 \ droite) & f (1,0) \\ f \ left (-1, \ frac {1} {2} \ right) & f \ left (- \ frac {1} {2}, \ frac {1} {2} \ right) & f \ left (0, \ frac {1} {2} \ right) & f \ left (\ frac {1} {2}, \ frac {1} {2} \ right) & f \ left (1, \ frac {1} {2 } \ droite) \\ f (-1,1) & f \ gauche (- \ frac {1} {2}, 1 \ droite) & f (0,1) & f \ gauche (\ frac {1} { 2}, 1 \ droite) & f (1,1) \\ \ end {array} \ droite)$$

Ou, si nous excluons les valeurs limites qui sont toujours nulles, les coordonnées seront calculées par la formule

$$

$$\ frac {2 taille-index + 1} {taille}$$

et la matrice prendra donc la forme

$$

$$\ left (\ begin {array} {ccccc} f \ left (- \ frac {4} {5}, - \ frac {4} {5} \ right) & f \ left (- \ frac {2} { 5}, - \ frac {4} {5} \ right) & f \ left (0, - \ frac {4} {5} \ right) & f \ left (\ frac {2} {5}, - \ frac {4} {5} \ right) & f \ left (\ frac {4} {5}, - \ frac {4} {5} \ right) \\ f \ left (- \ frac {4} {5 }, - \ frac {2} {5} \ right) & f \ left (- \ frac {2} {5}, - \ frac {2} {5} \ right) & f \ left (0, - \ frac {2} {5} \ right) & f \ left (\ frac {2} {5}, - \ frac {2} {5} \ right) & f \ left (\ frac {4} {5}, - \ frac {2} {5} \ right) \\ f \ left (- \ frac {4} {5}, 0 \ right) & f \ left (- \ frac {2} {5}, 0 \ right ) & f (0,0) & f \ left (\ frac {2} {5}, 0 \ right) & f \ left (\ frac {4} {5}, 0 \ right) \\ f \ left ( - \ frac {4} {5}, \ frac {2} {5} \ droite) & f \ left (- \ frac {2} {5}, \ frac {2} {5} \ right) & f \ gauche (0, \ frac {2} {5} \ droite) & f \ gauche (\ frac {2} {5}, \ frac {2} {5} \ droite) & f \ left (\ frac {4} {5}, \ frac {2} {5} \ right) \\ f \ left (- \ frac {4} {5}, \ frac {4} {5} \ right) & f \ left (- \ frac {2} {5}, \ frac {4} {5} \ right) & f \ left (0, \ frac {4} {5} \ right) & f \ left (\ frac {2} {5}, \ frac {4} {5} \ right) & f \ left (\ frac {4} {5}, \ frac {4} {5} \ right) \\ \ end {array} \ right)$$

Une fois les éléments de la matrice calculés par la formule, il est nécessaire de calculer leur somme et d'y diviser la matrice. Par exemple, si nous obtenons une matrice

$$

$$\ left (\ begin {array} {ccc} 1 & 4 & 1 \\ 4 & 20 & 4 \\ 1 & 4 & 1 \\ \ end {array} \ right)$$

alors la somme de tous ses éléments sera de 40, et après normalisation, elle prendra la forme

$$

$$\ left (\ begin {array} {ccc} \ frac {1} {40} & \ frac {1} {10} & \ frac {1} {40} \\ \ frac {1} {10} & \ frac {1} {2} & \ frac {1} {10} \\ \ frac {1} {40} & \ frac {1} {10} & \ frac {1} {40} \\ \ end {array } \ droite)$$

et la somme de tous ses éléments devient 1.

Atténuation linéaire

Tout d'abord, prenez la fonction la plus simple - la ligne:

$$

$$\ left \ {\ begin {array} {ll} 1-x, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

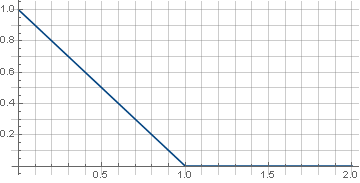
Une définition continue par morceaux nécessite ici que la fonction soit garantie de passer à zéro et qu'aucun artefact n'apparaisse aux coins de la matrice pendant la rotation. De plus, comme la rotation utilise la racine de la somme des carrés des coordonnées, qui est toujours positive, il suffit de déterminer la fonction uniquement dans la partie positive des valeurs. En conséquence, nous obtenons:

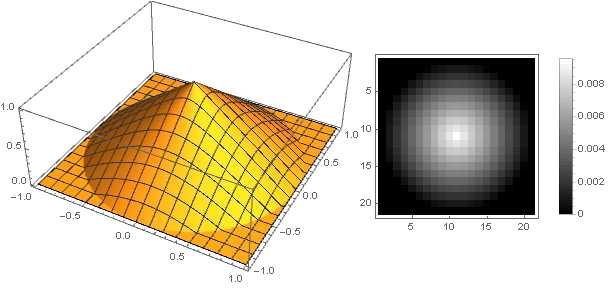
Atténuation linéaire douce

Une transition nette d'une ligne oblique à des fonctions nulles peut provoquer une contradiction avec un sens de la beauté. Pour le résoudre, la fonction aidera

$$

$$1- \ frac {n x-x ^ n} {n-1}$$

dans lequel $$$n$détermine la «rigidité» de l'amarrage, $$$n> 1$. Par exemple $$$n = 3$nous obtenons

$$

$$\ left \ {\ begin {array} {ll} 1- \ frac {3 xx ^ 3} {2}, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

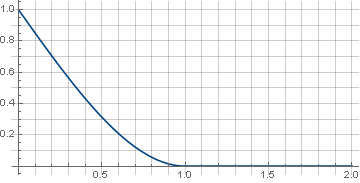
et le filtre lui-même ressemblera

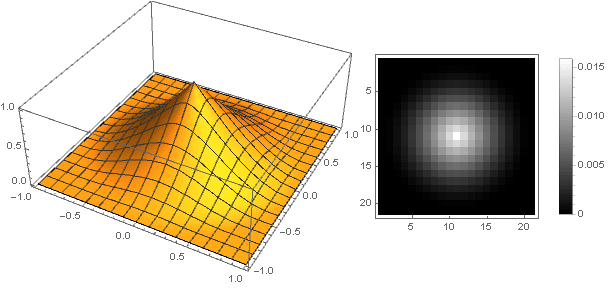
Atténuation hyperbolique

Le filtre peut être rendu plus "net" et aller plus facilement à zéro en prenant une autre fonction, par exemple une hyperbole, et en assurant une transition en douceur vers zéro en additionnant avec une parabole.



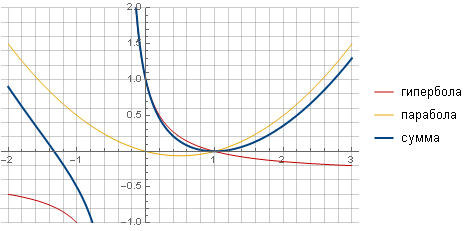
Après tous les calculs et simplifications, on obtient la formule

$$

$$\ left \ {\ begin {array} {ll} \ frac {(x-1) ^ 2 (k x + k + 1)} {(k + 1) (k x + 1)}, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

dans quel paramètre $$$k> 0$détermine la nature de l'atténuation:



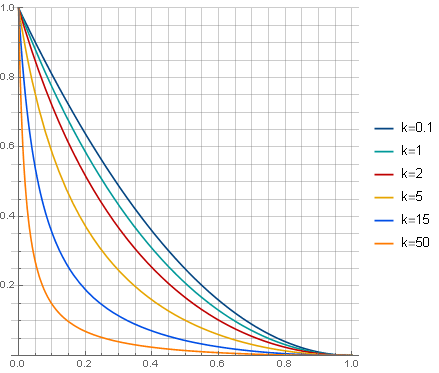
et le filtre lui-même se penchera (pour $$$k = 5$) comment

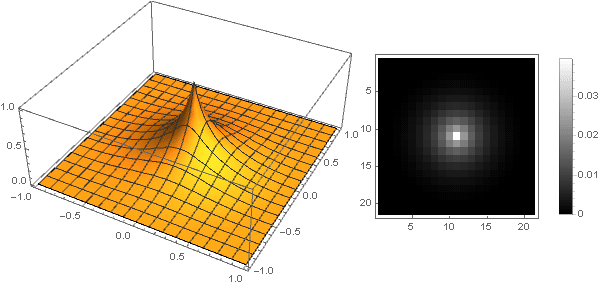
Effet bokeh

Vous pouvez aller d'une autre manière - pour rendre le haut du filtre non pointu, mais stupide. La façon la plus simple de mettre en œuvre cela est de définir la fonction d'amortissement comme constante:

$$

$$\ left \ {\ begin {array} {ll} 1, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

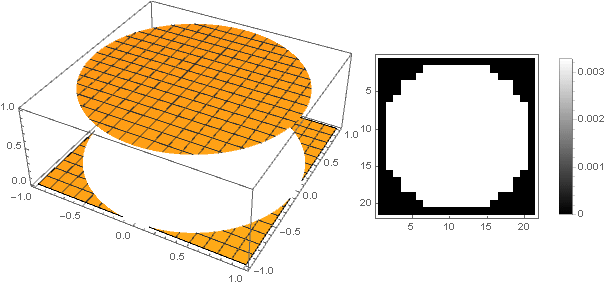
Mais dans ce cas, nous obtenons une forte pixellisation, ce qui contraste avec le sens de la beauté. Pour la rendre plus lisse sur les bords, une parabole d'ordre supérieur nous aidera, à partir de laquelle, en la déplaçant le long de l'axe des ordonnées et en la quadrillant, nous obtenons

$$

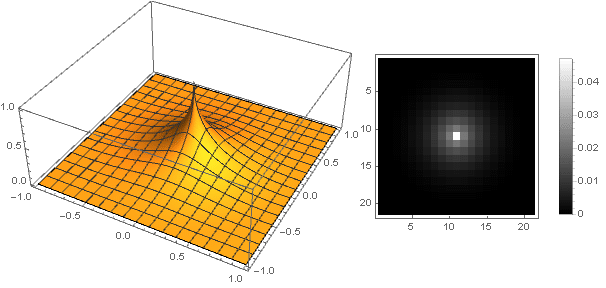
$$\ left \ {\ begin {array} {ll} \ left (1-x ^ n \ right) ^ 2, & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

Paramètre variable $$$n$Vous pouvez obtenir un large éventail d'options de filtrage:

$$

$$n = 0,5$$

$$

$$n = 2$$

$$

$$n = 10$$

$$

$$n = 50$$

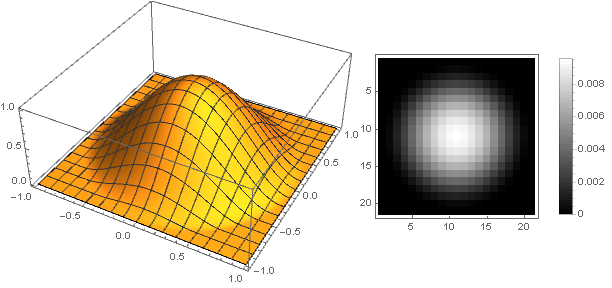
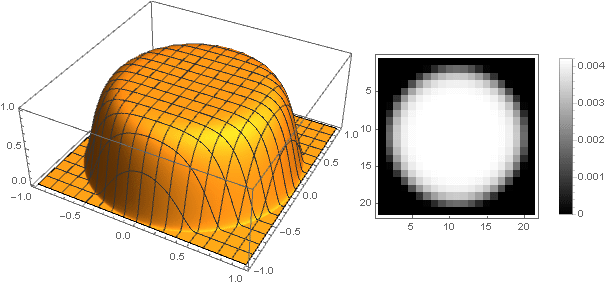
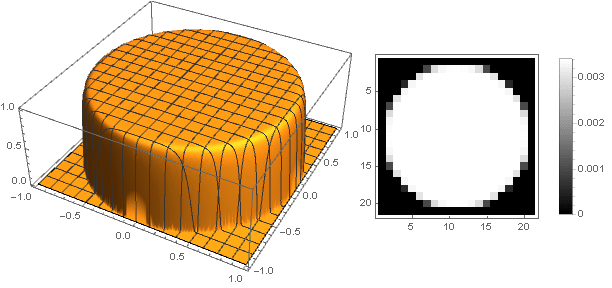
En modifiant légèrement la fonction d'amortissement, vous pouvez rendre l'anneau sur les bords du filtre plus prononcé, par exemple comme ceci:

$$

$$\ left \ {\ begin {array} {ll} \ left (1-x ^ n \ right) ^ 2 \ left (d + x ^ m \ right), & x <1 \\ 0, & x \ geqslant 1 \\ \ end {array} \ right.$$

Ici le paramètre $$$d$détermine la hauteur du centre, et $$$m$- la netteté de la transition vers les bords.
Pour $$$d = 0,2, m = 2, n = 10$nous obtenons



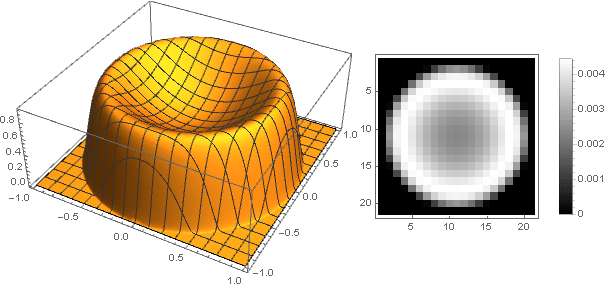
mais pour $$$d = 0, m = 12, n = 2$

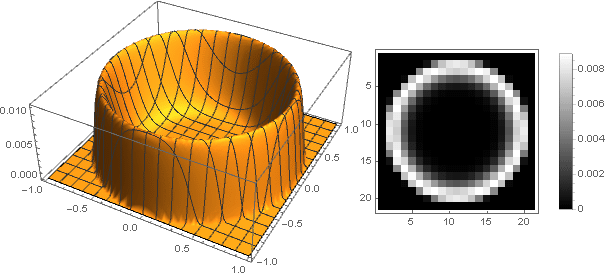
Variations gaussiennes

La fonction du gaussien lui-même peut également être modifiée directement. La façon la plus évidente de le faire est de paramétrer l'exposant - nous ne l'examinerons pas maintenant, mais prenons une option plus intéressante:

$$

$$\ left \ {\ begin {array} {ll} e ^ {\ frac {kx ^ 2} {x ^ 2-1}}, & -1 <x <1 \\ 0, et sinon \\ \ end { tableau} \ à droite.$$

En raison du fait qu'avec $$$x$dénominateur unitaire $$$x ^ 2-1$tend à zéro fraction $$$\ frac {k x ^ 2} {x ^ 2-1}$tend à moins l'infini, et l'exposant lui-même tend également à zéro. Divisant ainsi par $$$x ^ 2-1$permet de compresser le domaine de définition de fonction avec $$$(- \ infty, \ infty)$avant $$$(- 1,1)$. De plus, lorsque $$$x = \ pm 1$en raison de la division par zéro ( $$ ) la valeur de la fonction n'est pas définie, mais a deux limites - la limite d'une part (de l'intérieur) est zéro, et d'autre part, l'infini:

$$

$$\ underset {x \ to 1 ^ -} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = 0$$

$$

$$\ underset {x \ to 1 ^ +} {\ text {lim}} e ^ {\ frac {k x ^ 2} {x ^ 2-1}} = \ infty$$

Puisque les valeurs limites ne sont pas incluses dans l'intervalle, alors zéro dans la limite d'un seul côté est tout à fait suffisant. Fait intéressant, cette propriété s'étend à toutes les dérivées de cette fonction, ce qui garantit une correspondance parfaite avec zéro.

Paramètre $$$k$détermine la similitude avec le gaussien - plus il est grand, plus la similitude est forte - en raison du fait qu'une section de plus en plus linéaire $$$\ frac {1} {x ^ 2-1}$tomber au centre de la fonction. On pourrait supposer qu'à cause de cela, à la limite, vous pouvez obtenir le gaussien d'origine - mais, malheureusement, non - les fonctions sont toujours différentes.



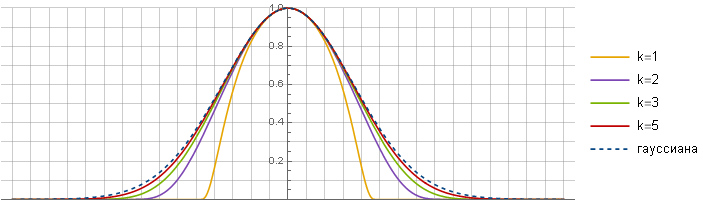
Vous pouvez maintenant voir ce qui s'est passé:

$$

$$k = 5$$

$$

$$k = 2$$

$$

$$k = 0,5$$

$$

$$k = 0,1$$

$$

$$k = 0,01$$

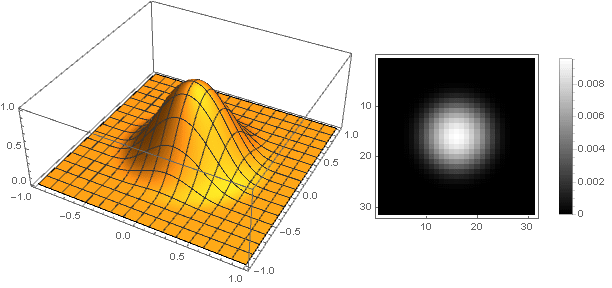
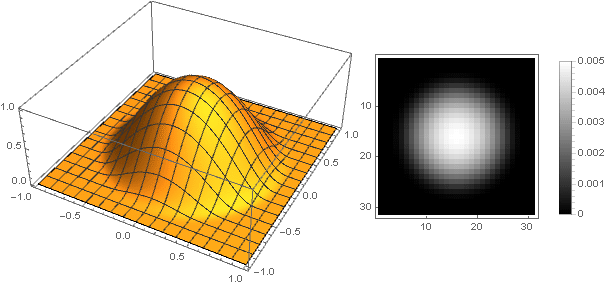
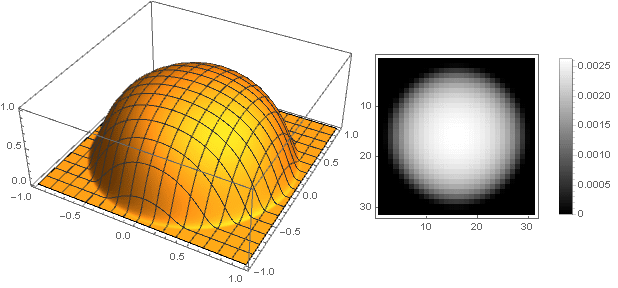
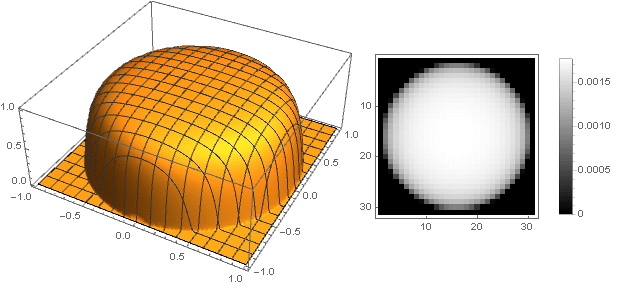
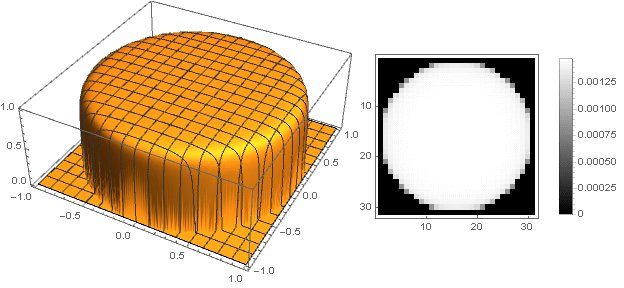
Variations de forme

En changeant la fonction de transition de deux coordonnées à une $$$\ sqrt {x ^ 2 + y ^ 2}$, vous pouvez obtenir d'autres formes, pas seulement un disque. Par exemple:

$$

$$f \ gauche (\ frac {\ gauche | x-y \ droite | + \ gauche | x + y \ droite |} {2} \ droite)$$

$$

$$f (\ gauche | x \ droite | + \ gauche | y \ droite |)$$

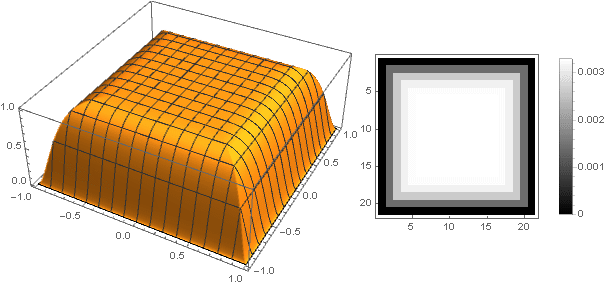
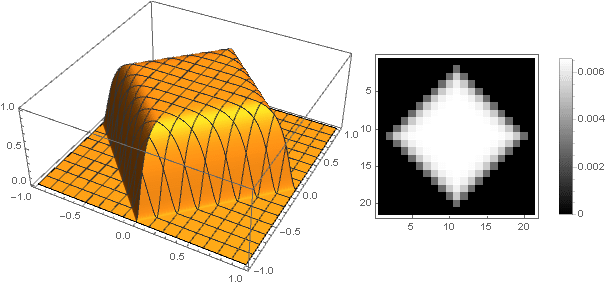
En passant à des nombres complexes, vous pouvez construire des figures plus complexes:

$$

$$f \ left (\ frac {\ left | \ Re \ left ((x + iy) (-1) ^ {\ frac {0} {3}} \ right) \ right | + \ left | \ Re \ left ((x + iy) (-1) ^ {\ frac {1} {3}} \ right) \ right | + \ left | \ Re \ left ((x + iy) (-1) ^ {\ frac { 2} {3}} \ droite) \ droite |} {\ sqrt {3}} \ droite)$$

$$

$$f \ biggl (10 \ left | \ Re \ left ((x + iy) (-1) ^ {\ frac {1} {8}} \ right) \ right | \ biggr) \ cdot f (\ left | x + iy \ droite |)$$

$$

$$f \ biggl (\ biggl | 5 \ left | x + iy \ right | (x + iy) \ Re \ biggl (\ cos \ left (\ frac {5} {2} \ arg (x + iy) \ right ) \ biggr) \ biggr | \ biggr) \ cdot f (\ left | x + iy \ right |)$$

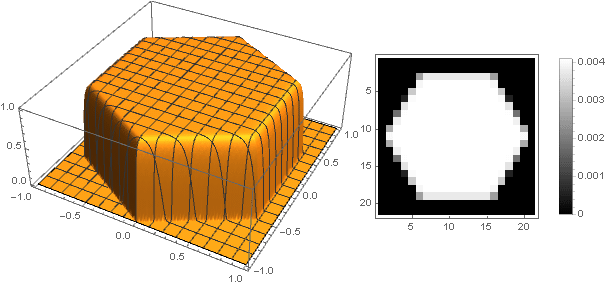
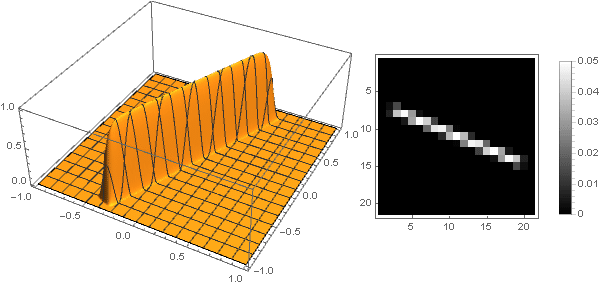
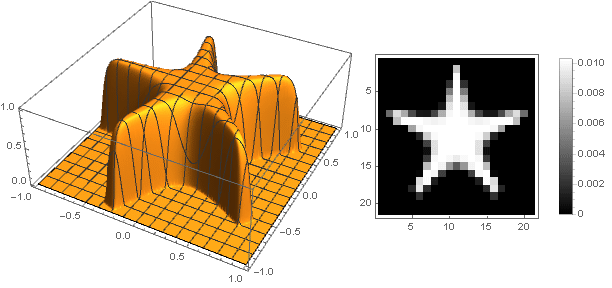
Dans ce cas, vous devez vous assurer que lors de la conversion des coordonnées ne dépassent pas l'intervalle $$$(0,1)$- bien, ou vice versa, redéfinissez la fonction d'amortissement pour les valeurs négatives de l'argument.

Quelques exemples spécifiques

Un article ne serait pas complet sans des tests pratiques sur des images spécifiques. Comme nous n'avons pas de travail scientifique, nous ne prendrons pas non plus l'image de Lena - nous prendrons quelque chose de doux et de moelleux:


















Les mêmes filtres, mais pour le texte:

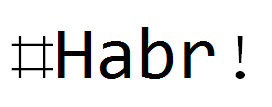
Conclusion

De même, vous pouvez créer des filtres plus complexes, y compris ceux avec une netteté ou des contours; et également modifier ceux déjà considérés.

Le filtrage non linéaire est particulièrement intéressant, lorsque les valeurs des coefficients de filtrage dépendent des coordonnées ou de l'image filtrée directement - mais c'est déjà un sujet pour d'autres études.

Plus en détail, la dérivation des fonctions d'ancrage avec une constante est considérée ici . Les fonctions de fenêtre considérées ici peuvent également être utilisées comme fonction d'atténuation - il suffit de mettre à l'échelle l'argument c (0,1) à ( $$$\ frac {1} {2}$, 1) ou considérer initialement les fonctions de fenêtre par la formule $$$\ frac {1} {2} \ left (f \ left (\ frac {t x + 1} {t-1} \ right) -f \ left (\ frac {t x-1} {t-1} \ droite) \ droite)$.

Le document source de Wolfram Mathematica pour cet article peut être téléchargé ici .