Théorie du bonheur. Vol vertigineux d'un sandwich au beurre

Je continue de familiariser les lecteurs de Habr avec les chapitres de son livre "Theory of Happiness" avec le sous-titre "Mathematical Foundations of the Laws of Meanness". Ce livre de science populaire n'est pas encore publié, racontant de manière très informelle comment les mathématiques vous permettent de regarder le monde et la vie des gens avec un nouveau degré de conscience. C'est pour ceux qui s'intéressent à la science et pour ceux qui s'intéressent à la vie. Et puisque notre vie est complexe et, dans l'ensemble, imprévisible, l'accent dans le livre est principalement sur la théorie des probabilités et les statistiques mathématiques. Ici les théorèmes ne sont pas prouvés et les fondements de la science ne sont pas donnés, ce n'est en aucun cas un manuel, mais ce qu'on appelle la science récréative. Mais c'est précisément une telle approche presque ludique qui nous permet de développer l'intuition, d'égayer les cours pour les étudiants avec des exemples vivants et, enfin, d'expliquer aux non-mathématiciens et à nos enfants ce que nous avons trouvé si intéressant dans notre science sèche.



Dans ce chapitre, nous examinons la loi d'un sandwich et organisons toute une étude en utilisant la méthode de Monte Carlo et l'analyse dimensionnelle. Et enfin, démystifiez le mythe populaire selon lequel le pétrole est la cause de cette loi de la méchanceté.

Le thème de la chute des sandwichs ne hante ni le grand public ni les chercheurs. Pendant des décennies, des expériences ont été menées, des films ont été tournés, des articles rédigés, un sandwich tombant recouvert de légendes et de conclusions incorrectes. Peu de tâches sans valeur ont attiré autant d'attention, et si vous pensez que tout cela est chouchoutant, alors gardez à l'esprit que même les récompenses ne sont pas non plus sérieuses, pour sa solution. En 1995, Robert Matthews a reçu le prix Shnobel pour son travail «Falling Sandwich, Murphy's Law et Fundamental Constants», publié dans le European Journal of Physics. Malgré le sujet comique et la réaction correspondante de la communauté scientifique, il s'agit d'un article tout à fait intéressant dans lequel une analyse approfondie du processus de glissement est effectuée et une conclusion de grande portée est tirée: peu importe sur quoi apparaissent les créatures anthropomorphes qui vivent dans l'atmosphère, elles seront condamnées à la loi d'un sandwich. Après un tel triomphe de recherches inutiles, on pourrait clore le sujet, mais pourquoi manquer l'occasion de considérer des méthodes intéressantes et objectivement utiles comme exemple d'un problème intéressant!

Ida lance des sandwichs à Monte Carlo!

Nous jetons rarement des sandwichs comme une pièce, du moins lorsque nous vieillissons de plus de deux ans. Le plus souvent, nous répétons involontairement la même expérience: un sandwich, placé à l'origine avec le beurre vers le haut, glisse hors de nos mains ou glisse sur la table. En train de glisser, il se tord, vole dans les airs et, enfin, se laisse tomber sur la table ou sur le sol. Le stade initial de la chute est affecté par un certain nombre de paramètres: le frottement contre les doigts ou la surface de la table, la position initiale du sandwich et sa vitesse initiale, la hauteur de la chute et enfin la taille du sandwich. Nous avons un système dynamique avec plusieurs paramètres d'entrée et une sortie - la position du sandwich au sol. À l'intérieur du système, comme dans le cas d'une pièce de monnaie, les lois mécaniques fonctionnent, qui sont décrites par des équations différentielles et elles sont déterministes . Cela signifie qu'il n'y a pas d'accident en eux - le résultat ne dépend que des données d'entrée, et avec la répétition exacte des paramètres, nous devrions obtenir des résultats identiques. Cela s'applique au modèle sandwich, présenté sous la forme d'un système d'équations différentielles, mais qu'en est-il des vrais sandwichs, bruts et uniques, déposés par de vraies personnes dans les restaurants, dans la rue ou sur le canapé? La variabilité du monde réel peut être décrite en appliquant des paramètres aléatoires à l'entrée du système déterministe.

Cependant, même l'algèbre des variables aléatoires, qui ne comprend que l'addition et la multiplication, n'est pas une tâche facile, mais nous avons des équations différentielles! Nous ne montons pas dans ces étendues sauvages fascinantes, mais utilisons la technique bien développée dans de nombreux domaines - la méthode de Monte Carlo . Elle consiste à accumuler des statistiques et à déterminer les propriétés d'un certain système complexe à la suite de tests répétés avec divers paramètres aléatoires. Je souligne encore une fois: le système à l'étude n'est pas stochastique et pas chaotique, et il réagit de manière prévisible aux données d'entrée aléatoires. Dans la méthode de Monte Carlo, l'aléatoire n'est nécessaire que pour trier efficacement autant d'options que possible et examiner tous les «angles» réalistes, en se faisant une idée du comportement du système.

En fait, nous avons déjà utilisé cette méthode, en observant les cyclistes sur une colline et nous continuerons à l'utiliser en fixant une date limite au bureau et en partageant de l'argent dans une société fermée. La correspondance biunivoque entre la probabilité et la mesure de volume ou de surface, dont nous avons parlé plus haut, nous permet d'utiliser la méthode de Monte Carlo pour l'intégration numérique. Une caractéristique de l'expérience sandwich à venir est que nous ne nous intéresserons pas à la distribution de probabilité (exacte ou empirique), mais à la dépendance de la probabilité sur les paramètres du problème. Nous chercherons la réponse à la question: dans quelles circonstances la loi sandwich est-elle respectée? Nous fournirons divers paramètres spécifiques à l'entrée de notre système dynamique et collecterons des statistiques sur les baisses et les baisses d'huile. Ainsi, le résultat d'une série d'expériences sera un nombre - la probabilité d'une chute d'huile.

Je suis convaincu que laisser délibérément de vrais sandwichs sur le sol est mauvais, nous allons donc utiliser la modélisation mathématique. Pour résoudre le problème de la chute d'un sandwich, j'ai choisi l' un des simulateurs du monde physique disponibles qui sont utilisés pour créer des jeux en ligne. Il a permis de créer une table et un plancher virtuels, ainsi que deux sandwichs. L'un est apparu sur le bord de la table, et le second - "glissé hors de ses doigts", c'est-à-dire glissé d'un support ponctuel. Il est de mon pouvoir de définir la position et l'angle initiaux du sandwich, la vitesse horizontale (cas de l'écrasement du sandwich sur la table), les coefficients de frottement, la taille du sandwich et la hauteur de la chute. Les expériences ressemblent à ceci:

Expériences avec la chute de sandwichs virtuels dans un simulateur du monde physique.

Au moment où le sandwich touche le sol, l'angle du sandwich est fixe, ou plutôt l'angle du vecteur qui lui est normal. Le signe du sinus de cet angle nous dira de quel côté l'huile s'est détournée: un cas réussi correspond à une valeur positive, et une position baissière correspond à une valeur négative. Le résultat est entré dans le tableau et le nouveau sandwich virtuel est prêt à tomber. La tâche que nous nous fixons est la suivante: évaluer la probabilité qu'un sandwich tombe du pétrole lorsqu'il tombe d'une hauteur donnée.

La méthode de Monte Carlo suppose que des variables aléatoires sont utilisées comme paramètres. Et ici, il vaut la peine de dire quelques mots sur ce qu'est une variable aléatoire . Revenons aux mathématiciens et aux structures mathématiques. Quelle structure peut-on utiliser pour simuler les résultats d'une chute d'un nombre sur un dé, ou du niveau d'eau dans une rivière, car il y a une excitation constante sur l'eau? Comment travailler avec le nombre de voitures passant l'intersection en une heure? Quelle structure peut décrire l'état d'un électron? D'une part, ce sont des nombres spécifiques d'un ensemble de valeurs bien défini: pour un os, par exemple, d'un ensemble $$$\ {1,2,3,4,5,6 \}$ , et cette valeur est facile à obtenir en menant une expérience. Cependant, une deuxième expérience donnera un résultat différent, ce n'est clairement pas seulement un nombre: aujourd'hui c'est un, demain c'est un autre. Une question philosophique peut même se poser: est-il judicieux de parler d'une valeur exacte du "niveau d'eau dans la rivière", ou du nombre de voitures, car ces valeurs ne peuvent pas être "capturées" et enregistrées? Pourrait-il y avoir, en quelque sorte, une connaissance exacte d'une variable aléatoire?

Souvent, lorsque l'on parle de telles variables aléatoires, elles ne sont limitées qu'à la valeur moyenne, mais c'est un excellent moyen de se confondre, voire de se confondre intentionnellement. Deux chiffres: la moyenne et l'écart-type, sont déjà meilleurs, mais ce ne sont clairement pas toutes les informations sur l'objet qui nous intéresse. Ce ne sont peut-être pas des nombres, mais des ensembles? Dites, vous pouvez essayer de décrire le niveau d'eau dans la rivière comme un intervalle de valeurs possibles, en tenant compte de l'excitation, et pour un exemple avec des voitures, disons que de 1 à 100 voitures passent en une heure, etc. Mais il est facile de voir que l'ensemble des valeurs possibles n'est pas non plus suffisant, par exemple, avec la répétition répétée de la mesure du nombre de voitures dans la rue, certains nombres se produiront plus souvent, d'autres nous n'attendrons pas du tout. Dans le dernier chapitre, nous avons introduit une mesure de probabilité en fonction d'un espace de probabilité. Pour une quantité aléatoire, les événements élémentaires de cet espace seront les éléments de son domaine de définition, et la mesure détermine la distribution de probabilité de cette quantité. Et maintenant, ce sont des informations exhaustives et précises. Une fonction peut être représentée analytiquement ou comme approximation par une autre fonction, sous la forme d'un tableau, d'un histogramme ou sous la forme d'un graphique. Toutes ces représentations sont des modèles du même objet - une variable aléatoire, et la chose la plus importante ici n'est pas tant le type spécifique de représentation que les propriétés mathématiques de cette fonction. Pour les distributions de probabilité, les propriétés sont différentes: le nombre de paramètres, le nombre de modes, l'entropie, la divisibilité infinie, l'additivité, la stabilité, l'intégrabilité, etc. La modélisation d'une variable aléatoire inconnue obtenue à partir de l'expérience, les statistiques d'un énorme arsenal de distributions connues avec des propriétés définies avec précision, sélectionne moins la fonction `` la plus similaire '', mais plutôt une fonction qui coïncide le mieux avec ses propriétés avec la variable aléatoire observée. C'est l'essence de l'analyse statistique et des techniques de test d'hypothèses statistiques qui sont familières à chaque élève qui a touché les statistiques.

Nous avons maintenant un problème, dans un sens, le contraire. Nous devons définir les paramètres du sandwich avec des variables aléatoires, n'ayant pas de données statistiques, mais guidés par les propriétés nécessaires de ces quantités. Il s'agit d'une partie importante et intéressante de la méthode de Monte Carlo, dont dépendent à la fois la solution et son exactitude.

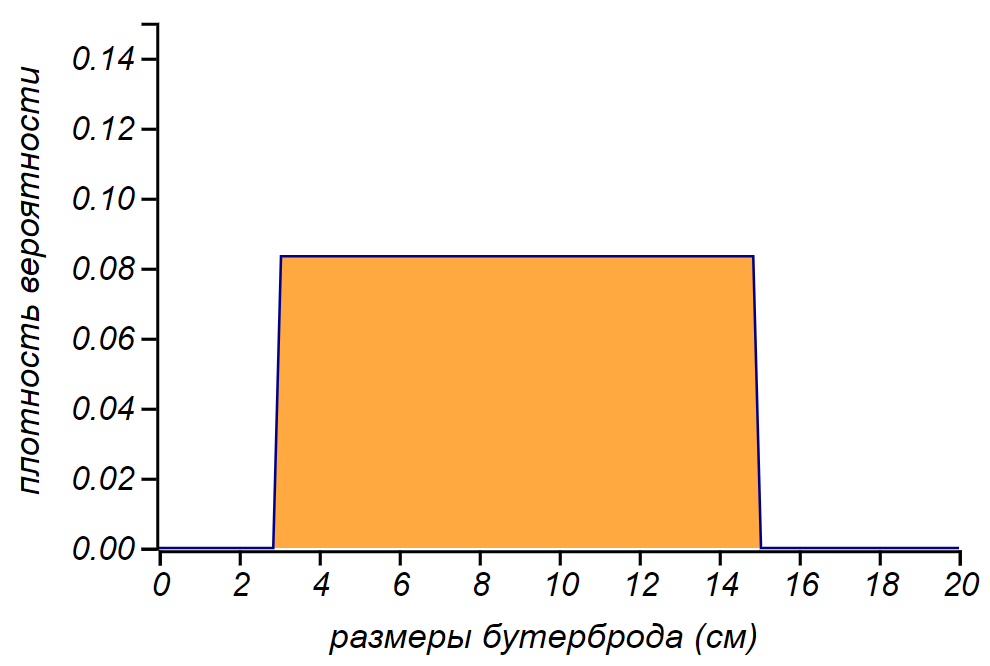1. Les dimensions du sandwich. Que peuvent-ils être? Les canapés de taille raisonnable ont un centimètre $$$3$ large, et un bon élève "bast" peut avoir des centimètres $$ . Le plus souvent, les sandwichs ont des tailles de $$ avant $$ Dans ce cas, la probabilité de rencontrer un sandwich de largeur millimétrique ou mètre, dans un sens pratique, est nulle. Je ne peux rien dire de plus sur les sandwichs et j'accepterai la taille des sandwichs uniformément répartis dans la plage spécifiée. Le choix est imparfait, mais on trouve plus souvent des sandwichs normaux que des sandwichs minuscules ou géants. Mais plus tard, nous verrons que ce point faible peut être gracieusement contourné.

2. Position de départ. Ici, sans plus tarder, nous allons définir une distribution uniforme pour déplacer le sandwich sur le bord de la table, si seulement il tombe.

3. Le coefficient de frottement. Il s'agit d'une quantité sans dimension, qui ne dépend que du matériau. Les tables et les nappes sont différentes, les doigts pressent un sandwich avec des forces différentes. Plage de coefficients de $$ avant $$ , alors que des valeurs extrêmes sont peu probables, en moyenne, vous pouvez vous attendre à quelque chose $$ . Toute distribution asymétrique en forme de cloche d'une valeur non négative, par exemple, une distribution gamma ou une log-normale, nous sera utile.

4. Vitesse initiale. Nous lançons rarement des sandwichs à grande vitesse, et le plus souvent nous ne les jetons pas du tout, mais cela arrive cependant. Tout ce que l'on sait de l'amplitude de la vitesse, c'est qu'elle est positive et on peut supposer qu'en glissant, en moyenne, on se déplace comme des mains moyennes, c'est-à-dire à une vitesse d'environ $$ m / s Si seulement cela est connu sur une quantité, alors il est raisonnable de la décrire par une distribution exponentielle (pourquoi, nous parlerons plus tard quand nous apprendrons l'entropie des distributions). Son mode est nul, donc la proportion de sandwichs qui sont tombés sans une grande vitesse initiale sera assez décente. Dans la "queue" seront des sandwichs, lancés par inadvertance en vol en fouettant des miettes de la table.

5. Nous fixerons la hauteur de la table, y déposerons une centaine de sandwichs, compterons le nombre d'huile tombée et la mettrons dans le tableau, ou refléterons la probabilité de la hauteur sur le graphique.

Voici les probabilités de laisser tomber un sandwich avec du beurre que nous obtenons:

La probabilité que des sandwichs à l'huile atterrissent différents sandwichs avec des conditions différentes selon la hauteur de la chute. Pour chaque hauteur $$ tests.

Une certaine tendance est visible, mais une diffusion très large s'est révélée. Lors de la moyenne, il s'avère que la probabilité de la hauteur de chute est presque indépendante et ne dépasse guère la moitié. Pouvez-vous faire confiance à une telle expérience? Est-ce qu'il réfute la loi d'un sandwich? Peut-être que nous n'avons pas jeté assez de sandwichs - il y avait tellement de données bruyantes! Augmentons le nombre de lancers et voyons ce qui se passe:

La probabilité qu'un pétrole atterrisse sur divers sandwichs calculée pour un plus grand nombre de tests (500 pour chaque hauteur).

Il y a moins d'émissions, mais il est encore plus clair que la loi du sandwich est très, très faible. Mais avons-nous effectué nos expériences correctement? La méthode de Monte-Carlo semble d'une simplicité séduisante: sachez vous-même remplacer les données horribles et voyez ce qui se passe. Les mathématiques sont une chose honnête: quel genre de question est-elle prête à donner quel genre de réponse . Mais si cette réponse a du sens dépend de la question.

Avant de commencer les expériences, pas aussi ludiques que les nôtres, mais réelles et coûteuses, à l'aide d'un satellite en orbite, d'un accélérateur de particules ou de mille vrais sandwichs à l'huile, il est nécessaire de réaliser des travaux préparatoires. Et l'une des façons puissantes et belles de comprendre comment mener une expérience correctement est d' analyser les dimensions du problème.

Nous avons modélisé un sandwich par des coordonnées généralisées, des impulsions et des forces - quantités physiques, qui, à leur tour, sont reliées par des équations de la mécanique analytique. En physique, les quantités quantitatives avec lesquelles nous traitons, que nous mesurons et substituons dans les équations, ne "rentrent" pas dans les nombres ordinaires - elles ont une structure supplémentaire, qui est appelée dimension . Toutes les expressions mathématiques correctes n'ont pas de sens si des quantités dimensionnelles y participent. Disons que cela n'a aucun sens d'ajouter de la vitesse et de la masse, il est impossible de comparer la force et la distance. Cependant, nous pouvons considérer le produit de la vitesse et de la masse, ayant reçu une nouvelle quantité dimensionnelle - l'élan, ou l'élan; il est possible de quadriller la vitesse et de la diviser par la distance, obtenant ainsi une valeur ayant la dimension d'accélération.

L'analyse des dimensions et la théorie de la similitude sont nées depuis longtemps, depuis l'époque de Lord Rayleigh. Ils sont utilisés en mécanique, en électrodynamique, en astrophysique et en cosmologie, permettant d'aborder des tâches complexes avec une élégance effrayante. Cependant, la recherche dans ce domaine n'est pas terminée et une définition rigoureuse de la structure formée par des quantités quantitatives (dimensionnelles) n'a été donnée qu'en 2016 par le mathématicien espagnol Alvaro Raposo.

Les contraintes imposées par les dimensions aux formules physiques sont souvent perçues par les élèves et les étudiants comme un désordre supplémentaire qui doit être surveillé. Mais d'un autre côté, les contraintes logiquement cohérentes sont extrêmement utiles! Ils filtrent les expressions incorrectes, ils vous permettent de «prédire» la structure de la solution d'un problème physique avant sa solution détaillée, ils sont un outil puissant dans la planification et l'analyse des données expérimentales.

Mais c'est intéressant. Nous avons calculé la chute du sandwich dans le programme, en utilisant des nombres non dimensionnels mais ordinaires. Comment «effacer» une grandeur physique d'une dimension et la transformer en nombre? À cette fin, nous connaissons les unités de mesure des grandeurs physiques familières: tous ces mètres, livres, minutes et newtons. Les unités de mesure prennent la partie dimensionnelle de la quantité, nous laissant avec un facteur - un nombre réel, qu'un ordinateur peut déjà gérer. Par exemple, la vitesse dans la direction sélectionnée est $$ km / h peut être représenté par le nombre $$ . Mais il y a une subtilité: la représentation numérique dépend du choix des unités de mesure. Si vous sélectionnez d'autres unités (par exemple, mètres et secondes) , la même vitesse sera représentée par un nombre différent: $$ . Les nombres sont différents, mais la quantité est un, et cela ne dépend pas de notre choix d'unités.

La question se pose: existe-t-il en quelque sorte un «meilleur» système d'unités? Il s'avère qu'il existe, pour cela, lors de la résolution du problème, il est nécessaire d'utiliser les quantités dimensionnelles incluses dans le problème comme unités de mesure.

Dans ce chapitre, nous avons des sandwichs volant, dans le précédent volant des pièces, nous donnons un autre exemple volant. Comment comparer les qualités de vol de différents oiseaux? Il est clair que les vitesses de développement des oiseaux sont différentes: pour un pigeon - $$90 km / h, à toute vitesse -$90$$$140 km / h, pour grues, moineaux ou canards colverts -$140$$$50 km / h, pour les colibris -$50$$$80 km / h Mais tous ces oiseaux varient considérablement en taille et en mode de vol. Si la longueur d'un perroquet est mesurée en perroquets et que le temps est mesuré en périodes de battement d'ailes, vous pouvez obtenir une certainevitesse, comme on dit. Vous pouvez diviser les vitesses que ces oiseaux peuvent développer en valeurs propres et obtenir une vitesse sans dimension qui montre combien de temps le corps peut voyager dans un volet des ailes. Voici le résultat de cette comparaison:$80$

l'oiseau	vitesse, km / h	longueur du corps	fréquence de balayage, 1 / s	, /
	140	18	5	0,9	43
	90	30	5	1,5	17
	80	8	200	16	1,4
	50	1	2,5	2,5	5
	50	40	9	3,6	3,8
	46	12	13	1,6	8

On peut voir que le martinet est à juste titre considéré comme le meilleur flyer, mais le colibri consomme de l'énergie de manière inefficace, cependant, cet oiseau n'a pas la tâche de voler pendant longtemps, comme une colombe. Les mêmes vitesses absolues de la grue, du moineau et du canard diffèrent considérablement lorsqu'elles sont traduites en quantités sans dimension. Ce type de calcul est utilisé pour simuler un vrai gros avion, en testant un petit modèle dans une soufflerie. Si tous les paramètres adimensionnels de ces deux systèmes sont proches, ils peuvent être considérés comme physiquement similaires et la modélisation est logique. Nous avons déjà utilisé cette approche, reflétant les unités relatives au lieu des unités absolues sur les diagrammes de Lorenz. Cela nous a permis de comparer entre eux divers phénomènes et distributions.

Il est clair quel sera le système d'unités le plus approprié lors de l'analyse du vol d'un sandwich. Bien sûr, la longueur doit être mesurée en sandwich. Pour une unité de temps, on peut prendre la valeur$$√l / g où$\sqrt{l/g}$$$l est la longueur du sandwich, et$l$$$g est l'accélération de la gravité. Et la hauteur de la table ne doit pas être mesurée en mètres, mais dans ses propres unités. Ayant ainsi obtenu le résultat, nous pouvons immédiatement le généraliser à la fois au cas des canapés et à une "chaussure de bâti" solide. Donc, nous répétons les calculs, mais sur le graphique, nous reflétons la hauteur du tableau en unités relatives. Si nous avons tout fait correctement, alors pour deux sandwichs de tailles différentes, nous devrions obtenir des graphiques très similaires. Voyons cela:$g$

La probabilité qu'un sandwich à l'huile atteigne une certaine valeur fixe, à différentes hauteurs d'incidence, calculée en unités relatives. Les points bleus correspondent à un sandwich d'une taille de 5 cm, les points rouges correspondent à 10 cm

Dans la formulation initiale, nous avons trié différentes tailles et reçu un nuage de résultats dans lequel la dépendance qui nous intéressait était cachée. Avec une augmentation du nombre de tests, nous avons moyenné ce nuage et reçu une réponse sans intérêt. Afin de montrer plus clairement en quoi consistait l'erreur méthodologique, imaginons que nous voulons calculer la probabilité qu'un sandwich tombe du beurre, en regardant au hasard les conditions et tailles initiales du sandwich et sa hauteur. Cela équivaut à faire la moyenne de tous les résultats que nous avons obtenus à la fois. En conséquence, nous obtenons un terrain d'entente confiant - une probabilité très proche de$$1 / 2 , comme dans le tirage au sort! C'est un résultat très logique et attendu, mais il est complètement inintéressant. En faisant la moyenne d'un grand nombre de données pour différentes tailles, nous sommes déjà proches de cette conclusion. Mais si le but de la modélisation est d'identifier les modèles, il est logique de minimiser le nombre de paramètres. Les données effacées parlent désormais clairement en faveur de la loi de la méchanceté, la limitant cependant à une certaine gamme de hauteurs: de$1/2$

$$2 à$2$$$$6$ la taille du sandwich (de la hauteur du coude au-dessus de la table à la hauteur des bras d'une personne debout). En dehors de cette plage, le sandwich a plus de chances de tourner le côté droit avant de tomber.

Mais que faire si vous regardez plus loin et jetez des sandwichs par la fenêtre? Il est clair que lors d'une chute d'une grande hauteur, peu importe de quel côté il se transformera en sandwich, et la résistance à l'air stabilise la chute, mais théoriquement, qu'espérons-nous voir? Probablement, certaines fluctuations de probabilité devraient être observées à mesure que le temps de vol augmente. Voyons voir:
La probabilité d'atterrissage d'un sandwich à l'huile lors d'une chute d'une hauteur élevée.

Nous avons deviné la fréquence, mais il est curieux que l'amplitude diminue et que les fluctuations de probabilité convergent vers $$ . De quoi peut-il parler? Est-ce le même effet que dans le cas d'une pièce, quand avec une augmentation de la durée du vol les conséquences des déviations des conditions initiales deviennent plus importantes? Il s'avère que dans ce cas la nature de l'égalisation des probabilités est différente.

Une analyse un peu plus dimensionnelle

Peu importe la frivolité du sujet de notre livre, nous parlons le langage des mathématiques et il s'efforce de trouver des solutions exactes. La méthode de Monte Carlo nous a permis d'avoir une idée de la solution, mais c'est ce qu'on appelle la force brute. Ce n'est pas aussi intéressant que du moins certains, mais une solution analytique. Une analyse des dimensions nous permettra d'obtenir une forme théorique de la dépendance obtenue par la méthode de Monte Carlo. Pour cela, nous n'avons pas besoin de résoudre des équations différentielles; de plus, toutes nos considérations ne dépassent pas les limites de relations complètement primitives et évidentes. C'est le charme de l'analyse dimensionnelle, qui, cependant, ressemble parfois à une astuce. Commençons donc, en nous limitant, par souci de simplicité, à ne glisser qu'un sandwich de longueur $$$l$ depuis la table des hauteurs $$$H$ avec une vitesse horizontale nulle.

1. L'angle de rotation du sandwich tombant dépend du temps et de la vitesse angulaire:

$$

$$\ varphi = t \ omega.$$

2. La vitesse angulaire est égale au produit du temps de glissement et de l'accélération angulaire:

$$

$$\ omega = t_0 \ varepsilon.$$

3. Le temps de glissement peut être exprimé en termes d'accélération de la gravité et d'une partie de la longueur du sandwich qui est entré en contact avec la table dans la proportion suivante:

$$

$$t_0 \ propto \ sqrt {\ frac {l_0} {g}}.$$

Ici $$$l_0$ - la longueur du sandwich posé sur la table. Ici, nous utilisons la relation de proportionnalité indiquée par le signe $$$\ propto$ . Expression $$$y \ propto x$ peut être remplacé par $$$y = C x$ où $$$C$ - une constante inconnue. J'adore vraiment cette attitude. La proportionnalité «intègre» tout ce qui se complique qui se transforme en constante: à la fois le fait que le moment de gravité change pendant la rotation et le centre de rotation change lors du glissement. Tout cela, bien sûr, vous devez savoir pour un calcul précis, mais le résultat n'est qu'un coefficient sans dimension, et dans notre analyse, il ne joue aucun rôle. Avec une seule icône, nous nous sommes sauvés d'une intégration fastidieuse.

4. L'accélération angulaire se produit à partir de l'accélération de la gravité et dépend de l'épaule à laquelle la gravité est appliquée:

$$

$$\ varepsilon \ propto \ frac {g} {l-l_0}.$$

Et encore le signe $$$\ propto$ nous a permis de ne pas calculer le moment d'inertie de la plaque pour l'axe situé dans son plan, ainsi que la projection changeante de la gravité (ce sont deux intégrales de plus).

5. Enfin, le temps de chute dépend de la hauteur de la table et de l'accélération de la gravité:

$$

$$t \ propto \ sqrt {\ frac {H} {g}}.$$

6. En substituant toutes ces expressions dans la première formule, on obtient un résultat simple:

$$

$$\ varphi \ propto \ sqrt {\ frac {l_0 H} {l (l-l_0)}},$$

qui, si vous mesurez toutes les longueurs dans les sandwichs, se transforme en

$$

$$\ varphi \ propto \ sqrt {\ frac {x h} {1-x}}.$$

Ici $$$l_0 = x l$ et $$$H = h l$ . Eh bien, tout converge - l'angle est sans dimension et cela dépend de coefficients sans dimension. Cet angle ne dépend pas de l'échelle de temps, la géométrie pure reste. Le dénominateur n'est pas dangereux lorsque $$$x> 0,5$ le sandwich ne tombera pas du tout (nous envisageons une vitesse horizontale nulle), donc $$ .

De quel côté le sandwich tombera est déterminé par le signe du sinus de l'angle $$$\ varphi$ c'est-à-dire la fonction $$$\ mathrm {sign} (\ sin \ varphi)$ . Cette fonction renvoie $$$-1$ pour le cas de "oil up" et $$$1$ pour "huile vers le bas." Nous pouvons utiliser cette fonction pour exprimer la probabilité de chute d'un sandwich déterministe si nous le portons à une plage de $$$0$ avant $$$1$ :

$$

$$P _ {\ downarrow} (x, h) = \ frac12 \ left [1+ \ mathrm {sign} (\ sin \ varphi) \ right] = \ frac12 \ left \ {1+ \ mathrm {sign} \ left [ \ sin \ left (C \ sqrt {\ frac {xh} {1-x}} \ right) \ right] \ right \},$$

où la flèche indique symboliquement la position de l'huile. Coefficient $$$C$ qui apparaît dans la formule de probabilité exprime tout ce qui reste caché à l'aide du signe proportionnel. C'était en effet une démarche très délicate, elle nous a sauvés d'une intégration fastidieuse (et même de trois), mais comment savoir maintenant à quoi correspond ce coefficient? De l'expérience, d'ailleurs, une seule expérience de mesure de l'angle au moment de la chute suffit pour obtenir une estimation de cette valeur! En utilisant le simulateur, j'ai facilement constaté que $$$C = 2,3$ .

La tâche suivante consiste à exprimer mathématiquement ce que les positions initiales $$$x$ peut être différent. Nous sommes intéressés par la probabilité qu'un sandwich fasse tomber du beurre si $$$x$ sera égal $$ ou $$ ou n'importe quel nombre de $$$0$ avant $$ . Nous avons utilisé l'union «ou», et chacun de ces cas est considéré par nous comme indépendant et excluant tous les autres dans une expérience spécifique. Rappelez-vous que la probabilité est une mesure de l'espace de probabilité, et si c'est le cas, alors la probabilité est additive. Cela nous permet d'ajouter simplement les probabilités $$$P _ {\ downarrow} (x, h)$ , pour toutes les valeurs $$$x$ , multipliant à partir de précédemment par la probabilité de tomber dans une plage spécifique de valeurs. Nous séparons le segment de $$$0$ avant $$ sur $$$n$ parties, et calculer l'estimation de probabilité sous la forme d'une somme:

$$

$$P _ {\ downarrow} (h) \ sim \ frac {2} {n} \ sum \ limits_ {i = 0} ^ n P _ {\ downarrow} \ left (\ frac {i} {2n}, h \ right ),$$

voici le multiplicateur $$ exprime la probabilité d'une variable aléatoire $$$x$ entrer dans un morceau de largeur $$ . Voici à quoi ressemble le résultat pour un nombre important de partitions ( $$$n = 100$ ) et une série d'expériences numériques à vitesse horizontale nulle:

Évaluation théorique et expérimentale de la probabilité qu'un pétrole atterrisse un sandwich lorsqu'il tombe d'une grande hauteur. La vitesse horizontale initiale dans les expériences est nulle.

La solution que nous avons présentée précédemment contient plus de paramètres aléatoires, elle s'est donc avérée plus lissée et proche de $$ . Mais, en principe, l'analyse dimensionnelle peut être effectuée pour un cas plus général.

Veuillez noter que la probabilité $$$P _ {\ downarrow}$ approche avec l'augmentation $$$h$ à des valeurs proches de $$ . Et ce n'est pas du tout dû à l'incertitude et à l'influence des erreurs initiales. Les calculs ont montré que cela est le résultat de l'ajout des nombreuses harmoniques formées par les valeurs $$$x$ lors de la sommation $$$P _ {\ downarrow} (x, h)$ . Si nous oublions le malheureux sandwich et continuons le programme $$$P _ {\ downarrow}$ , nous voyons alors que l'estimation de probabilité continuera de fluctuer si près $$ , cherchant progressivement cette valeur.

Est-il possible de savoir sans calculs directs si la probabilité continuera de converger vers $$ ou va-t-il jamais repousser? Et dans ce phénomène, il y a aussi une place pour les mathématiques non triviales et profondes. Le fait est que chaque valeur $$$x$ une certaine fréquence d'oscillations correspond, et l'ensemble constitue le soi-disant spectre de la fonction totale. Si le spectre est discret, c'est-à-dire qu'il est constitué de fréquences séparées, alors la fonction totale (on l'appelle la transformée de Fourier) sera périodique. À un spectre continu sous la forme d'une constante sur un segment de $$$0$ avant $$ correspondra une fonction apériodique correspondant à des oscillations décroissantes. Mais nous nous sommes penchés sur une nouvelle branche des mathématiques - l'analyse fonctionnelle .

Le grand Enrico Fermi, le grand-père de la méthode de Monte-Carlo (le mathématicien Stanislav Ulam est considéré comme le père), a enseigné à ses élèves à faire des évaluations simples, à trouver un morceau de papier ou des doigts, ce que nous attendons avant d'obtenir la solution exacte du problème. Il est merveilleux que si l'évaluation s'avère correcte, il deviendra clair que l'essence du problème est capturée, sinon, c'est le résultat le plus utile - cela signifie que la tâche s'est avérée plus intéressante qu'il n'y paraît!

Dans notre cas, une simple estimation suffit, le problème sandwich ne vaut pas une solution plus approfondie. La méthode de Monte Carlo ne nous a montré que des indices de la solution, et l'analyse dimensionnelle n'a montré qu'une partie de sa structure générale, mais ensemble, ils pourraient nous montrer comment fonctionne la probabilité souhaitée. L'érudition permet au mathématicien de voir des structures toutes faites dans les plans de la solution et de faire des hypothèses et des conclusions de grande portée.

Robert Matthews, dans son étude historique, a également utilisé l'analyse dimensionnelle pour montrer que la loi sandwich est fondamentale. Sa conclusion est basée sur le fait que la hauteur maximale d'un organisme qui a atteint ses membres postérieurs dans le but de prendre les membres antérieurs pour prendre un sandwich avec de l'huile est déterminée par les propriétés de résistance des tissus biologiques et de la gravité. À son tour, la taille caractéristique du sandwich devrait correspondre à l'échelle de la créature - et les nains sur certaines planètes lourdes et les dylds sur une planète à faible gravité choisiront des sandwichs pour eux-mêmes en taille. Nous arrivons ici à ce qu'on appelle la spéculation en science. Il ne s'agit pas d'une revente d'un bien à des prix exorbitants, mais d'hypothèses douteuses qui forment la base d'une construction logique. En particulier, nous supposons que les créatures ont des mains qui ont des proportions similaires aux nôtres, ce qui est plus que discutable.

À propos du pétrole et du vent

En merphologie, la citation incorrecte de la loi de X.L. Groupe Menka:

Les problèmes complexes ont toujours des solutions simples, faciles à comprendre et incorrectes.

Vous pouvez souvent entendre que la loi du sandwich est à blâmer pour l'huile, qui est plus dense que le pain et donc «l'emporte». Et bien que cela ne s'applique pas au sujet de notre livre, je souhaite analyser cette question afin d'y mettre un terme. Pour que quiconque puisse se référer plus tard au fait que «les scientifiques ont prouvé que la présence de pétrole n'affecte pas de quel côté les sandwichs gifles!»

Enfant, nous nous amusions en lançant une mouche de pigeon ou une plume de queue, coincée dans un morceau de pâte à modeler, un centimètre ou deux de diamètre, en hauteur. Il a volé jusqu'à quatre mètres, après quoi il est descendu magnifiquement et en douceur en autorotation, comme un hélicoptère avec un moteur étouffé. Ensuite, nous avons grandi et notre plaisir est devenu moins inoffensif. Nous avons acheté un écrou et y avons vissé deux boulons des côtés opposés, en comprimant la farce des têtes d'allumettes écrasées. Il restait à attacher une bande ou juste un morceau de corde à l'un des boulons, à détordre correctement et à courir dans le ciel pendant quinze mètres. À l'automne, un ruban léger a stabilisé la position verticale du projectile, procurant un impact de haute qualité sur l'asphalte et une petite explosion, déchirant parfois l'écrou en morceaux. (Faites attention si vous décidez de partager cette expérience d'enfance avec vos enfants!)

Dans les deux expériences, nous voyons qu'un stylo léger ou du ruban adhésif est rapidement apparu sur la partie lourde de l'appareil et a stabilisé la chute. Apparemment, cela conduit à une opinion intuitive selon laquelle le beurre lourd et le pain léger devraient également se comporter de cette manière. Imaginez un ballon: un panier plus dense est toujours situé sous un ballon moins dense. De plus, l'expérience suggère que si vous saisissez avec deux doigts le milieu géométrique d'un objet avec une masse répartie asymétriquement, alors il s'effondrera de sorte que la partie lourde soit au fond.

Mais ces deux phénomènes ne fonctionnent pas en cas de chute d'un sandwich.

Commençons par le deuxième processus - avec "l'emporter sur". Ce n'est pas par hasard que j'ai ennuyé de préciser: "... si vous prenez le milieu géométrique d'un objet ..", cela signifie que les points de tangence se situent sur une certaine droite formant l'axe de rotation passant par le centre de gravité de l' objet. Dans ce cas, en effet, une position stable sera celle dans laquelle le centre de gravité est en dessous de l'axe. Mais si l'axe de rotation formé par les doigts passe par le centre de gravité, alors le système sera en équilibre indifférent - il se moquera de la façon dont il est orienté.

Qu'est-ce qui fait qu'une plume avec un petit poids, une bombe à partir d'un écrou ou un ballon avec des ballons dans un panier vous fait naviguer de la manière «correcte»? De l'air. Il «tient» nos objets pour que l'axe passe au-dessus du centre de gravité. Plus précisément, un flux d'air venant en sens inverse qui crée une force répartie sur la zone du corps. Et le point conditionnel d'application de cette force sera situé près du centre géométrique du carré de la figure. Pour plus de clarté, nous allons dessiner les forces agissant sur le ballon conditionnel, comme sur un objet de densité inégale:

Les forces qui amènent le ballon dans une position stable.

Et un sandwich?

Premièrement, si nous «coupons» l'air, il tombera tout simplement. En chute libre, le corps tourne précisément autour du centre de masse, de sorte qu'il n'a aucune raison de tourner de façon particulière. Comme on dit à l'école: "Dans un ascenseur qui tombe, on observe une apesanteur." Le beurre dans le sandwich est tout aussi léger.

Une huile dense peut affecter le processus de glissement, elle élèvera efficacement le centre de masse au-dessus du toucher exact et changera l'expression pour l'accélération angulaire $$$l$ sur $$$\ sqrt {l ^ 2 + d ^ 2} = l \ sqrt {1+ \ delta ^ 2}$ où $$$\ delta = d / l$ - l'épaisseur relative du sandwich. Pour les petites valeurs $$$\ delta$ cette expression peut être calculée comme $$$l (1+ \ delta ^ 2/2)$ . On obtient, comme on dit, un effet de second ordre. Pour un sandwich avec un rapport largeur / épaisseur comme $$ à $$$1$ , les changements relatifs ne dépassent pas $$$2 \%$ . Et c'est la limite supérieure maximale de l'effet, car nous avons élevé le centre de masse à l'épaisseur du sandwich, ce qui correspond à une huile infiniment dense!

Maintenant, nous remettons l'air en marche, laissant la densité de l'huile infiniment plus élevée que la densité du pain. Nous avons une plaque mince et dense avec un parachute léger mais résistant à l'air. Alors que le plan du sandwich est horizontal, le moment des forces de résistance à l'air proportionnelles à la dérive agit sur lui - la zone avec laquelle le flux d'air interagit: $$$M _ {-} \ propto l ^ 2$ . En position verticale, la dérive diminuera et, en conséquence, le moment sera différent: $$$M_ {|} \ propto l d$ . Le rapport de ces points: $$$M_ {|} / M _ {-} \ propto \ delta.$ J'ai écrit un signe proportionnel ici, car les coefficients de résistance pour une plaque située à travers et le long du flux sont différents, et ils me sont inconnus. Mais ils ne sont pas nécessaires - il est déjà clair que l'effet de l'air en position verticale (c'est-à-dire qu'il rend la position de l'huile inégale) est plus faible qu'en position horizontale. Et maintenant, nous rappelons que le sandwich tourne, ce qui signifie qu'il se substitue au flux soit par l'extrémité, soit par le plan. Nous pouvons introduire une mesure de l'action des forces de résistance. Si la vitesse angulaire de rotation ne change pas de manière significative au cours d'une période (et c'est le cas pour l'air), alors il est logique de prendre comme mesure la variation de la quantité de mouvement angulaire proportionnelle à la durée de la force. À son tour, la période d'action est proportionnelle à l'angle «balayé» par le sandwich pendant cette période. En conséquence, des mesures des moments d'action $$$M_ {|}$ et $$$M _ {-}$ sera proportionnelle $$$M_ {|} \ varphi_ {|}$ et $$$M _ {-} \ varphi _ {-}$ où les angles qui balayent l'extrémité et le plan sont indiqués dans le dessin. 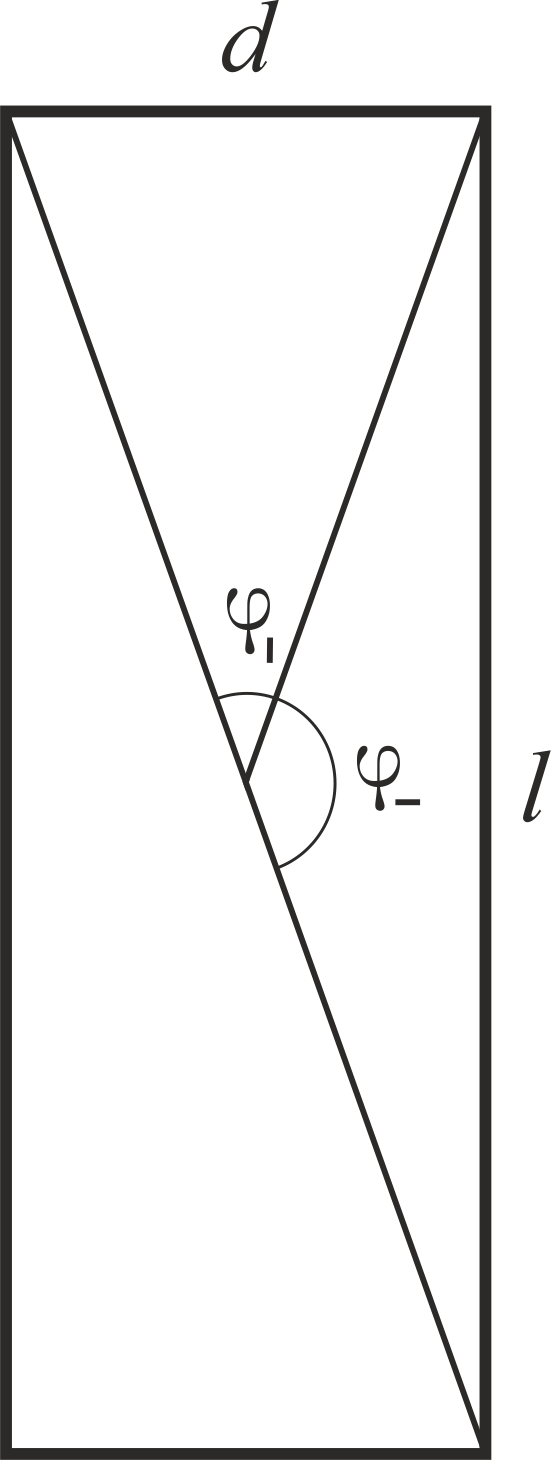Nous pourrions utiliser le travail des forces de résistance comme mesure et obtenir le même rapport. Le rapport d'angle est facile à calculer:

$$

$$\ frac {\ varphi_ {|}} {\ varphi _ {-}} = \ frac {\ varphi_ {|}} {\ frac {\ pi} {2} - \ varphi_ {|}}.$$

Au petit $$$d / l$ , $$$\ varphi_ {|} \ sim \ delta$ (on utilise la propriété de la tangente d'un petit angle $$ précision aux angles moins $$ ), et nous avons donc:

$$

$$\ frac {M_ {|} \ varphi_ {|}} {M _ {-} \ varphi _ {-}} \ sim \ delta \ frac {\ delta} {\ frac {\ pi} {2} - \ delta} \ propto \ delta ^ 2.$$

Encore une fois, il s'avère que l'effet de l'asymétrie pour un sandwich plat est limité par l'effet de second ordre. Typiquement, la densité du beurre n'est que le double de celle du pain, et le centre de déplacement de masse ne dépasse pas un tiers de l'épaisseur du sandwich avec une couche raisonnable de beurre ne dépassant pas l'épaisseur du pain. Cette observation réduira l’effet du pétrole à $$ .

S'il semblait au lecteur que nous tirions maintenant sur les moineaux avec le pistolet, je suis entièrement d'accord avec lui. Mais, premièrement, je ne veux pas en savoir plus sur l'huile «qui l'emporte», deuxièmement, je ne veux pas être sans fondement, et troisièmement, je voulais montrer comment le physicien estime les quantités, représentant le processus, mais n'ayant pas de données complètes. Bien sûr, au moment de l'atterrissage, le beurre peut coller au sol et empêcher le sandwich de sauter et de se renverser à nouveau, mais je ne démonterai certainement pas les mécanismes d'impact, de déformation élastique et de saut d'un morceau de pain. Donc, beaucoup d'analyses sont sorties pour ce problème. Et le deuxième Shnobelevskaya pour elle ne sera plus donné.

$$

$$* * *$$

Le but de notre chemin n'était pas aussi important: la réfutation ou la justification de la loi du sandwich, que le chemin lui-même. Il a montré comment la combinaison de différentes méthodes mathématiques vous permet d'examiner le problème sous différents angles et fournit des connaissances assez précises, même sans solution détaillée au problème. La cohérence des différentes disciplines mathématiques, approches et points de vue est la force et la beauté des mathématiques. Il convient de rappeler les merveilleuses paroles de Marina Tsvetaeva: "Je ne veux pas avoir un point de vue, je veux avoir la vue . " L'étude de divers domaines des mathématiques peut donner au chercheur une véritable vision multidimensionnelle «volumétrique», qui vous permet de regarder dans l'espace apparemment fermé et caché de la connaissance.