Réseaux de densité de mélange

Bonjour à tous!

Parlons, comme vous l'avez peut-être deviné, des réseaux de neurones et de l'apprentissage automatique. D'après le nom, il est clair ce qui sera dit sur les réseaux de densité de mélange, puis juste MDN, je ne veux pas traduire le nom et le laisser tel quel. Oui, oui, oui ... il y aura un peu de mathématiques ennuyeuses et de théorie des probabilités, mais sans cela, malheureusement ou heureusement, c'est à vous de décider s'il est difficile d'imaginer le monde de l'apprentissage automatique. Mais je m'empresse de vous rassurer, ce sera relativement petit et ce ne sera pas très difficile. Quoi qu'il en soit, vous pouvez l'ignorer, mais regardez juste une petite quantité de code en Python et PyTorch, c'est vrai, nous écrirons le réseau en utilisant PyTorch, ainsi que divers graphiques avec les résultats. Mais le plus important est qu'il y aura une opportunité de comprendre un peu et de comprendre ce que sont les réseaux MD.

Eh bien, commençons!

---

Régression

Pour commencer, rafraîchissons un peu nos connaissances et rappelons brièvement ce qu'est la régression linéaire .

Nous avons un vecteur $$$X = \ {x_1, x_2, ..., x_n \}$ nous devons prédire la valeur $$$Y$ , qui dépend en quelque sorte de $$$X$ en utilisant un modèle linéaire:

$$

$$\ hat {Y} = X ^ T \ hat {\ beta}$$

Comme fonction d'erreur, nous utiliserons l'erreur quadratique:

$$

$$SE (\ beta) = \ sum_ {i = 1} ^ n (y_i- \ hat {y} _i) ^ 2 = \ sum_ {i = 1} ^ N (y_i-x_i ^ T \ hat {\ beta} ) ^ 2$$

Ce problème peut être résolu directement en prenant la dérivée de SE et en mettant sa valeur à zéro:

$$

$$\ frac {\ delta SE (\ beta)} {\ delta \ beta} = 2X ^ T (\ mathbf {y} -X \ beta) = 0$$

Ainsi, nous trouvons simplement son minimum, et SE est une fonction quadratique, ce qui signifie que le minimum existera toujours. Après cela, vous pouvez déjà facilement trouver $$$\ beta$ :

$$

$$\ hat \ beta = (X ^ TX) ^ {- 1} X ^ T \ mathbf {y}$$

C'est tout, le problème est résolu. C'est là que nous finissons de rappeler ce qu'est la régression linéaire.

Bien sûr, la dépendance inhérente à la nature de la génération de données peut être différente et alors une certaine non-linéarité doit déjà être ajoutée à notre modèle. Résoudre le problème de régression directement pour des données volumineuses et réelles est également une mauvaise idée, car il existe une matrice $$$X ^ TX$ les dimensions $$$n \ fois n$ , et il faut encore trouver sa matrice inverse, et il arrive souvent qu'une telle matrice n'existe tout simplement pas. Dans ce cas, différentes méthodes basées sur la descente de gradient viennent à notre secours. La non-linéarité des modèles peut être implémentée de différentes manières, notamment en utilisant des réseaux de neurones.

Mais maintenant, ne parlons pas de cela, mais des fonctions d'erreur. Quelle est la différence entre SE et log-vraisemblance lorsque les données peuvent avoir une relation non linéaire?


Arrête ça! Probabilité? C'est quelque chose de la théorie des probabilités. C'est vrai - c'est une pure théorie des probabilités. Mais comment relier l'écart quadratique à la fonction de vraisemblance? Et comment ça se passe. Elle est liée à la recherche du maximum de vraisemblance (Maximum de vraisemblance) et à une distribution normale, pour être plus précis, à sa moyenne $$$\ mu$ .

Afin de réaliser qu'il en est ainsi, regardons à nouveau la fonction de déviation carrée:

$$

$$RSS (\ beta) = \ sum_ {i = 1} ^ n (y_i- \ hat {y} _i) ^ 2 \ qquad \ qquad (1)$$

Supposons maintenant que la fonction de vraisemblance ait une forme normale, c'est-à-dire une distribution gaussienne ou normale:

$$

$$L (X) = p (X | \ theta) = \ prod ^ X \ mathcal {N} (x_i; \ mu, \ sigma ^ 2)$$

En général, quelle est la fonction de vraisemblance et quelle est sa signification, je ne le dirai pas, vous pouvez en lire ailleurs, vous devez également vous familiariser avec le concept de probabilité conditionnelle, le théorème de Bayes, et bien plus encore, pour une compréhension plus approfondie. Tout cela entre dans la pure théorie des probabilités, étudiée à la fois à l'école et à l'université.

Maintenant, en se rappelant la formule de distribution normale, nous obtenons:

$$

$$L (X; \ mu, \ sigma ^ 2) = \ prod ^ X \ frac {1} {\ sqrt {2 \ pi \ sigma ^ 2}} e ^ {- \ frac {(x_i- \ mu) ^ 2} {2 \ sigma ^ 2}} \ qquad \ qquad (2)$$

Et si on mettait l'écart type $$$\ sigma ^ 2 = 1$ et supprimez toutes les constantes de la formule (2), supprimez simplement, ne réduisez pas, car trouver le minimum de la fonction ne dépend pas d'eux. Ensuite, nous verrons ceci:

$$

$$L (X; \ mu, \ sigma ^ 2) \ sim \ prod ^ Xe ^ {- (x_i- \ mu) ^ 2}$$

Toujours rien de tel? Non? Et si on prend le logarithme de la fonction? Du logarithme, en général, il y a quelques avantages: la multiplication se transformera en somme, un degré en multiplication, et $$$\ log {e} = 1$ - pour cette propriété, il convient de préciser que nous parlons du logarithme naturel et, à proprement parler $$$\ ln {e} = 1$ . Et en général, le logarithme d'une fonction ne change pas son maximum, et c'est la caractéristique la plus importante pour nous. La connexion avec Log-Lik vraisemblance et Probabilité et pourquoi cela sera utile sera décrite ci-dessous dans une petite digression. Et donc ce que nous avons fait: supprimé toutes les constantes et pris le logarithme de la fonction de vraisemblance. Ils ont également supprimé le signe moins, transformant ainsi Log-Likelihood en Log-Likelihood négatif (NLL), la connexion entre eux sera également décrite comme un bonus. En conséquence, nous avons obtenu la fonction NLL:

$$

$$\ log L (X; \ mu, I ^ 2) \ sim \ sum (X- \ mu) ^ 2$$

Jetez un autre coup d'œil à la fonction RSS (1). Oui, ce sont les mêmes! Exactement! On voit également que $$$\ mu = \ hat {y}$ .

Si vous utilisez la fonction d'écart type MSE, nous obtenons de ceci:

$$

$$\ operatorname {argmin} MSE (\ beta) \ sim \ operatorname {argmax} \ mathbb {E} _ {X \ sim P_ {data}} \ log P_ {modèle} (x; \ beta)$$

où $$$\ mathbb {E}$ - attente mathématique $$$\ beta$ - paramètres du modèle, nous les désignerons à l'avenir comme: $$$\ theta$ .

Conclusion: Si nous utilisons la famille LS comme fonctions d'erreur dans la question de régression, alors nous résolvons essentiellement le problème de trouver la fonction de vraisemblance maximale dans le cas où la distribution est gaussienne. Et la valeur prédite $$$\ chapeau {y}$ égale à la moyenne dans la distribution normale. Et maintenant, nous savons comment tout cela est connecté, comment la théorie des probabilités (avec sa fonction de vraisemblance et sa distribution normale) et les méthodes d'écart type ou OLS sont connectées. Plus de détails à ce sujet peuvent être trouvés dans [2].

Et voici le bonus promis. Puisque nous parlons des relations entre les différentes fonctions d'erreur, nous considérerons (pas nécessairement à lire):

Régression du réseau neuronal

Nous sommes donc arrivés à une pratique plus intéressante. Voyons comment vous pouvez résoudre le problème de la régression en utilisant des réseaux de neurones (réseaux de neurones). Nous allons implémenter tout dans le langage de programmation Python, pour créer un réseau que nous utilisons la bibliothèque d'apprentissage en profondeur PyTorch.

Génération de données source

Entrer les données $$$\ mathbf {X} \ in \ mathbb {R} ^ N$ générer en utilisant une distribution uniforme, prendre l'intervalle de -15 à 15, $$$\ mathbf {X} \ en U [-15, 15]$ . Des points $$$\ mathbf {Y}$ on obtient en utilisant l'équation:

$$

$$\ mathbf {Y} = 0,5 \ mathbf {X} + 8 \ sin (0,3 \ mathbf {X}) + bruit \ qquad \ qquad (3)$$

où $$$bruit$ Est un vecteur de bruit de dimension $$$N$ obtenu en utilisant la distribution normale avec des paramètres: $$$\ mu = 0, \ sigma ^ 2 = 1$ .



Le graphique des données reçues.

Création de réseaux

Créez un réseau de neurones à rétroaction régulière ou FFNN.


Notre réseau est constitué d'une couche cachée d'une dimension de 40 neurones et d'une fonction d'activation - tangente hyperbolique:

$$

$$\ tanh x = \ frac {e ^ x-e ^ {- x}} {e ^ x + e ^ {- x}} \ qquad \ qquad (4)$$

La couche de sortie est une transformation linéaire normale sans fonction d'activation.

Apprendre et obtenir des résultats

En tant qu'optimiseur, nous utiliserons AdamOptimizer. Le nombre d'époques d'étude = 2000, le taux d'apprentissage (taux d'apprentissage ou lr) = 0,1.


Examinons maintenant les résultats d'apprentissage.


Graphique des valeurs de la fonction MSE en fonction de l'itération de la formation; graphique des valeurs des données de formation et des données de test.


Résultats réels et prévus sur les données de test.

Données inversées

Nous compliquons la tâche et inversons les données.



Graphique de données inversé.

Pour la prédiction $$$\ mathbf {\ hat Y}$ utilisons le réseau de distribution direct de la section précédente et voyons comment il gère cela.

 inv_train_losses, inv_test_losses = train(net, x_train_inv, y_train_inv, x_test_inv, y_test_inv) 

Graphique des valeurs de la fonction MSE en fonction de l'itération de la formation; graphique des valeurs des données de formation et des données de test.


Résultats réels et prévus sur les données de test.

Comme vous pouvez le voir sur les graphiques ci-dessus, notre réseau n'a pas du tout géré ces données, il n'est tout simplement pas en mesure de les prédire. Et tout cela est arrivé parce que dans un tel problème inversé pour un point $$$x$ peut correspondre à plusieurs points $$$y$ . Vous demandez, qu'en est-il du bruit? Il a également créé une situation dans laquelle, pour une $$$x$ pourrait obtenir quelques valeurs $$$y$ . Oui, c'est vrai. Mais le fait est que, malgré le bruit, tout était une distribution définie. Et puisque notre modèle prédit essentiellement $$$p (y | x)$ , et dans le cas de MSE, c'était la valeur moyenne de la distribution normale (pourquoi elle est décrite dans la première partie de l'article), puis elle a bien fait face à la tâche «directe». Sinon, nous obtenons plusieurs distributions différentes pour une $$$x$ et en conséquence, nous ne pouvons pas obtenir un bon résultat avec une seule distribution normale.

Réseau de densité de mélange

Le plaisir commence! Qu'est-ce que le réseau de densité de mélange (ci-après réseau MDN ou MD)? En général, il s'agit d'un certain modèle capable de simuler plusieurs distributions à la fois:

$$

$$p (\ mathbf {y} | \ mathbf {x}; \ theta) = \ sum_k ^ K \ pi_k (\ mathbf {x}) \ mathcal {N} (\ mathbf {y}; \ mu_k (\ mathbf { x}), \ sigma ^ 2 (\ mathbf {x})) \ qquad \ qquad (5)$$

Quelle étrange formule, dites-vous. Voyons cela. Notre réseau MD apprend à modéliser la moyenne $$$\ mu$ et variance $$$\ sigma ^ 2$ pour plusieurs distributions. Dans la formule (5) $$$\ pi_k (\ mathbf {x})$ - les soi-disant facteurs de signification d'une distribution distincte pour chaque point $$$x_i \ in \ mathbf {x}$ , un certain facteur de mélange ou la contribution de chacune des distributions à un certain point. Total là-bas $$$K$ distributions.

Encore quelques mots sur $$$\ pi_k (\ mathbf {x})$ - en fait, c'est aussi une distribution et représente la probabilité que pour un point $$$x_i \ in \ mathbf {x}$ sera une condition $$$k$ .

Fuh, encore une fois, ce calcul, écrivons déjà quelque chose. Et donc, nous allons commencer à réaliser un réseau. Pour notre réseau nous prenons $$$K = 30$ .

 self.fc = nn.Linear(input_dim, layer_size) self.fc2 = nn.Linear(layer_size, 50) self.pi = nn.Linear(layer_size, coefs) self.mu = nn.Linear(layer_size, out_dim*coefs) # mean self.sigma_sq = nn.Linear(layer_size, coefs) # variance 

Définissez les couches de sortie pour notre réseau:

 x = F.relu(self.fc(x)) x = F.relu(self.fc2(x)) pi = F.softmax(self.pi(x), dim=1) sigma_sq = torch.exp(self.sigma_sq(x)) mu = self.mu(x) 

Nous écrivons la fonction d'erreur ou la fonction de perte, formule (5):

 def gaussian_pdf(x, mu, sigma_sq): return (1/torch.sqrt(2*np.pi*sigma_sq)) * torch.exp((-1/(2*sigma_sq)) * torch.norm((x-mu), 2, 1)**2) losses = Variable(torch.zeros(y.shape[0])) # p(y|x) for i in range(COEFS): likelihood = gaussian_pdf(y, mu[:, i*OUT_DIM:(i+1)*OUT_DIM], sigma_sq[:, i]) prior = pi[:, i] losses += prior * likelihood loss = torch.mean(-torch.log(losses)) 

Notre réseau MD est prêt à fonctionner. Presque prêt. Reste à la former et à regarder les résultats.



Le graphique des valeurs de la fonction de perte en fonction de l'itération de l'entraînement; le graphique des valeurs des données d'entraînement et des données de test.

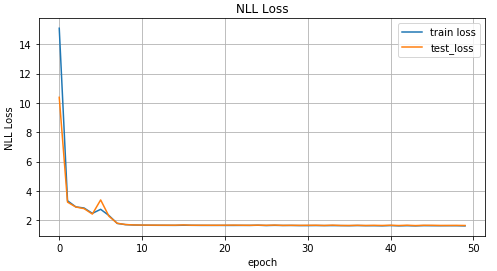
Puisque notre réseau a appris les valeurs moyennes de plusieurs distributions, regardons ceci:

 pi, mu, sigma_sq = mdn_net(Variable(torch.from_numpy(x_test_inv))) 

Graphique pour les deux valeurs moyennes les plus probables pour chaque point (à gauche). Graphique pour les 4 valeurs moyennes les plus probables pour chaque point (à droite).


Graphique pour toutes les valeurs moyennes pour chaque point.

Pour prédire les données, nous sélectionnerons aléatoirement plusieurs valeurs $$$\ mu$ et $$$\ sigma ^ 2$ basé sur la valeur $$$\ pi_k (\ mathbf {x})$ . Et puis en fonction d'eux pour générer des données cibles $$$\ chapeau {y}$ en utilisant une distribution normale.



Données prédites pour 10 valeurs sélectionnées au hasard $$$\ mu$ et $$$\ sigma ^ 2$ (à gauche) et pour deux (à droite).

Les chiffres montrent que MDN a fait un excellent travail avec la tâche «inverse».

Utiliser des données plus complexes

Voyons comment notre réseau MD gère les données plus complexes, telles que les données en spirale. L'équation de la spirale hyperbolique en coordonnées cartésiennes:

$$

$$x = \ rho \ cos \ phi \\\ qquad \ qquad \ qquad \ qquad \ qquad \ qquad (6) \\ y = \ rho \ sin \ phi \\ $$

Graphique des données en spirale.

Pour le plaisir, voyons comment un réseau Feed-Forward ordinaire fera face à une telle tâche.


Comme prévu, le réseau Feed-Forward n'est pas en mesure de résoudre le problème de régression pour ces données.

Nous utilisons le réseau MD décrit et créé précédemment pour la formation sur les données en spirale.


Mixture Density Network a fait un excellent travail dans cette situation.

Conclusion

Au début de cet article, nous avons rappelé les bases de la régression linéaire. Nous avons vu cela en commun entre trouver la moyenne pour la distribution normale et MSE. Démonté comment connecté NLL et entropie croisée. Et surtout, nous avons trouvé le modèle MDN, qui est capable d'apprendre des données obtenues à partir d'une distribution mixte. J'espère que l'article est compréhensible et intéressant, malgré le fait qu'il y ait eu un peu de maths.

Le code complet peut être consulté sur GitHub .

---

Littérature

1. Réseaux de densité de mélange (Christopher M. Bishop, Neural Computing Research Group, Dept. of Computer Science and Applied Mathematics, Aston University, Birmingham) - l'article décrit en détail la théorie des réseaux MD.
2. Moindres carrés et maximum de vraisemblance (MROsborne)