Un mathématicien amateur a découvert la plus petite couverture universelle

Grâce à des calculs géométriques difficiles, Philip Gibbs a découvert le plus petit revêtement connu pour toute forme possible.

Un couvercle universel tel qu'un hexagone peut être décrit autour de n'importe quelle forme.

Philip Gibbs n'est pas un mathématicien professionnel. Par conséquent, quand il voulait réfléchir à une tâche, il en recherchait une qu'un amateur puisse gérer. Il a découvert une tâche difficile qui peut rendre fou même les meilleurs esprits. Et dans un article publié cette année, Gibbs a fait des progrès significatifs dans la résolution de la question d'il y a cent ans, en fonction de la capacité de mesurer avec précision la zone jusqu'aux échelles atomiques.

Le premier à proposer ce problème a été le mathématicien français Henri Léon Lebesgue, dans une lettre à son ami Julius Pal, écrite en 1914. Lebesgue a demandé: quelle est la forme de la zone la plus petite possible, capable de couvrir complètement un grand nombre d'autres formes (ayant une propriété commune, qui est décrite ci-dessous)?

Au cours du siècle dernier, la tâche de trouver une couverture universelle s'est transformée en piège à souris: les progrès dans sa résolution, s'ils se sont produits périodiquement, ont toujours été incroyablement faibles. L'amélioration de Gibbs par rapport à cela est devenue spectaculaire - même si vous devez encore y réfléchir un peu.

Imaginez une douzaine de coupures de papier de différentes tailles et formes gisant sur votre sol. Imaginez maintenant qu'on vous propose de créer une autre forme suffisamment grande pour couvrir l'une des formes disponibles. Grâce à l'expérimentation - en superposant des formulaires et en les retournant - vous pouvez trouver un moyen de résoudre ce problème. Mais, ayant trouvé une couverture universelle, pouvez-vous être sûr d'avoir trouvé la plus petite? Vous pouvez imaginer qu'au cours de la journée, vous revenez périodiquement à votre formulaire et que vous avez la possibilité de couper des pièces supplémentaires ici et là.

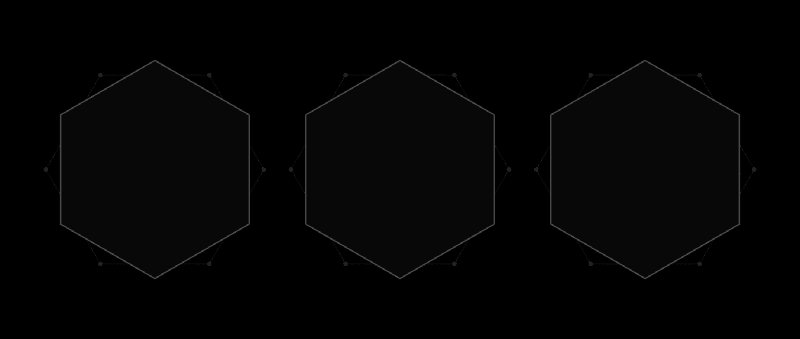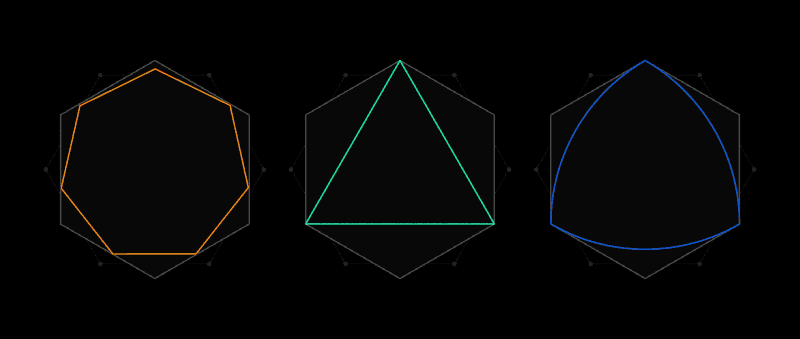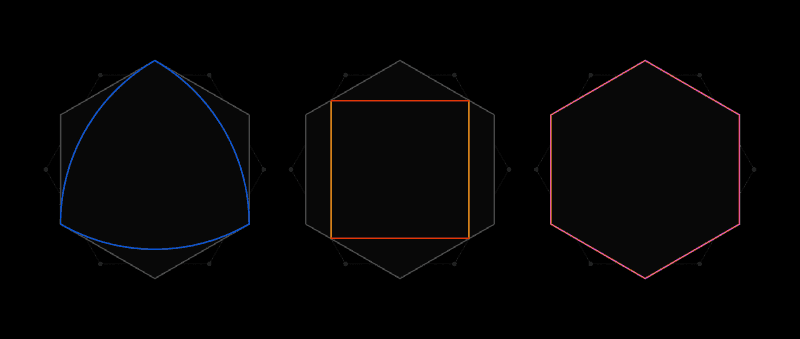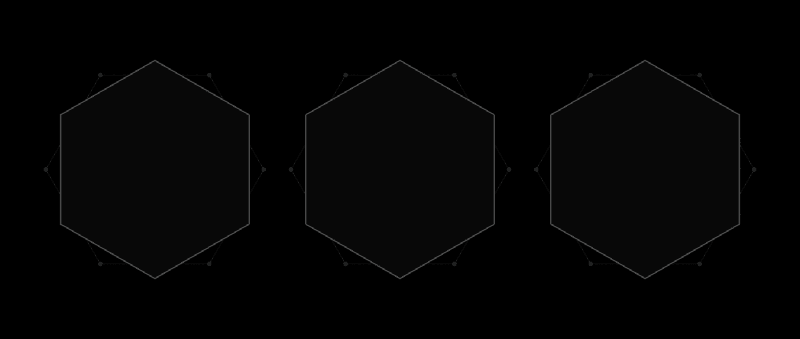
C'est l'esprit du problème de couverture universelle de Lebesgue. Au lieu des coupures de papier, il prend en compte les formes dans lesquelles deux points quelconques ne sont pas espacés de plus d'une unité de longueur. La forme la plus évidente sera un cercle de diamètre 1, mais il y en a un nombre infini: un triangle équilatéral, un pentagone régulier, un hexagone régulier, une forme triangulaire à côtés gonflés, connue sous le nom de triangle de Röhlo - et ce n'est que pour les débutants. La variété des formes rend difficile de trouver la plus petite couverture pour toutes.



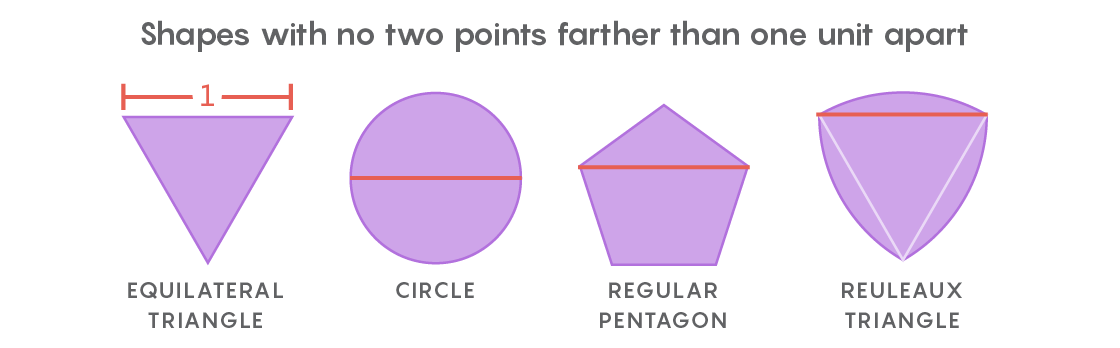
Peu de temps après avoir reçu une lettre de Lebesgue, Pal s'est rendu compte que l'hexagone régulier serait la couverture universelle. Et puis il a amélioré ce résultat, notant qu'en coupant deux coins de l'hexagone, ne se tenant pas côte à côte, vous pouvez obtenir une forme avec une zone plus petite, qui se révélera toujours être un revêtement universel.

«Prenez un hexagone, placez-en un deuxième dessus, tournez-le de 30 degrés et coupez deux coins. C'est là que Pal a terminé la recherche », a déclaré Gibbs.

Au cours des 80 années suivantes, deux autres mathématiciens ont coupé des bandes étroites de la couverture universelle de Pal. En 1936, Roland Sprag enlève un petit morceau à côté d'un des coins. En 1992, Hansen supprimera deux coins miniatures des coins inférieur droit et gauche. Les illustrations de Hansen pouvaient indiquer l'emplacement de ces pièces, mais pas leur taille: leur superficie était de 0,0000000000004 unité.



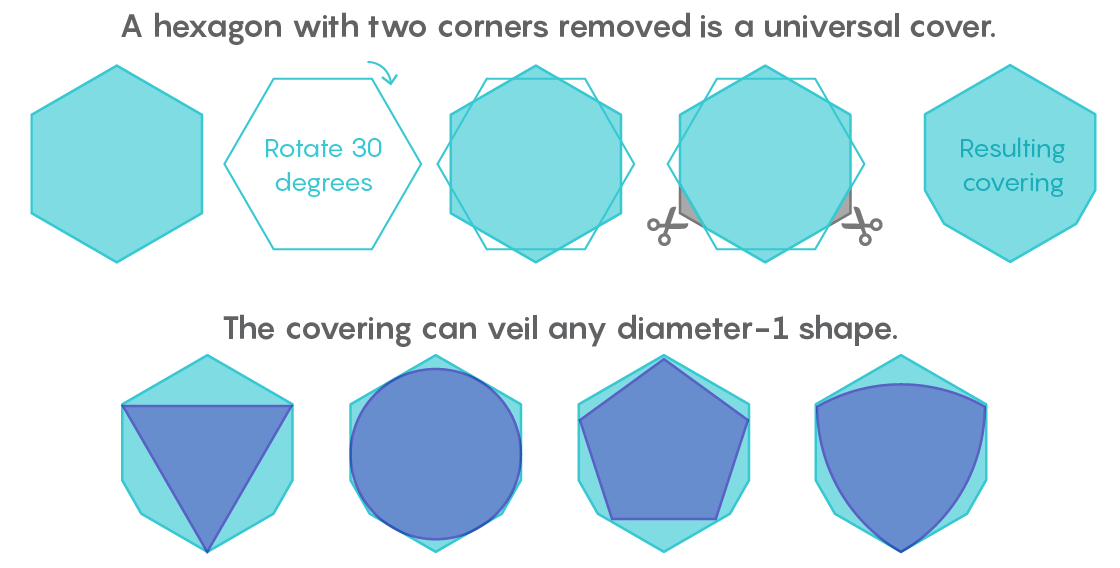
"Vous ne pouvez pas les dessiner sur une échelle, ils auraient la taille d'un atome", a déclaré John Baez , mathématicien à l'Université de Californie à Riverside.

Baez a sorti la tâche de Lebesgue de l'oubli lorsqu'il a écrit à ce sujet dans son blog sur les mathématiques populaires en 2013. Il a admis qu'il était fasciné par cette tâche d'une manière telle qu'une vidéo avec un insecte en train de se noyer pourrait vous fasciner. "Mon intérêt pour la tâche était malsain", a écrit BAez. "Je ne connais pas les raisons pour lesquelles cela pourrait être important." Je ne vois pas comment cela peut se connecter à de nombreuses autres tâches merveilleuses. Cela semble incroyablement complexe par rapport à la première impression. J'admire les gens qui y travaillent autant que j'admire les gens qui décident de traverser l'Antarctique à ski. »

Philip Gibbs n'a jamais traversé l'Antarctique à ski, mais lisez le blog Baez. Quand il a rencontré un record du problème de Lebesgue, il a pensé: "Eh bien, c'est exactement ce dont j'ai besoin."

Ciseaux atomiques

Gibbs pensait un jour qu'il pourrait devenir un scientifique. Il a obtenu un diplôme en mathématiques de l'Université de Cambridge et un doctorat en physique théorique de l'Université de Glasgow. Cependant, il a rapidement perdu son enthousiasme pour la recherche universitaire et est devenu programmeur. Il a travaillé sur des systèmes pour la conception de navires, la gestion du trafic aérien et les finances et, en 2006, il a pris sa retraite.

Gibbs est resté intéressé par les questions académiques, mais en tant que chercheur profane, il ne pouvait pas faire grand-chose. "Il est difficile pour un scientifique indépendant de suivre ce qui se passe", a-t-il déclaré. "Mais si vous trouvez le bon créneau, vous pouvez faire quelque chose et obtenir des résultats utiles."


Mathématicien amateur Philip Gibbs

Une telle niche était le problème de couverture universelle de Lebesgue. Cette tâche n'a jamais reçu l'attention des mathématiciens, il soupçonnait donc qu'il pourrait réaliser des progrès. Gibbs a également réalisé que son expérience en programmation pourrait être un avantage. «Je recherche toujours des problèmes dans lesquels les ordinateurs et les mathématiques expérimentales peuvent être utilisés», a-t-il déclaré.

En 2014, Gibbs a exécuté une simulation informatique pour 200 formes aléatoires de diamètre 1. À partir des simulations, il s'ensuit qu'il pourrait être en mesure de couper un petit morceau du coin supérieur de la plus petite couverture précédente. Il a transformé cela en preuve que le nouveau revêtement fonctionnera pour toutes les formes possibles de diamètre 1. Gibbs a envoyé la preuve à Baez, qui, avec l'une de ses élèves, Karina Baghdasaryan, a aidé Gibbs à donner à l'œuvre un style mathématique formel.

Les trois d'entre eux ont publié leurs travaux sur Internet en février 2015. Cela a réduit la zone de couverture universelle la plus petite possible de 0,8441377 à 0,8441153 unités. Les économies de 0,0000224 unités ont été presque un million de fois supérieures à ce que Hansen a réalisé en 1992.

Gibbs était convaincu qu'il pourrait améliorer le résultat. Dans un ouvrage publié en octobre, il a coupé un autre morceau relativement gros d'un revêtement universel, portant sa superficie à 0,84409359 unités.



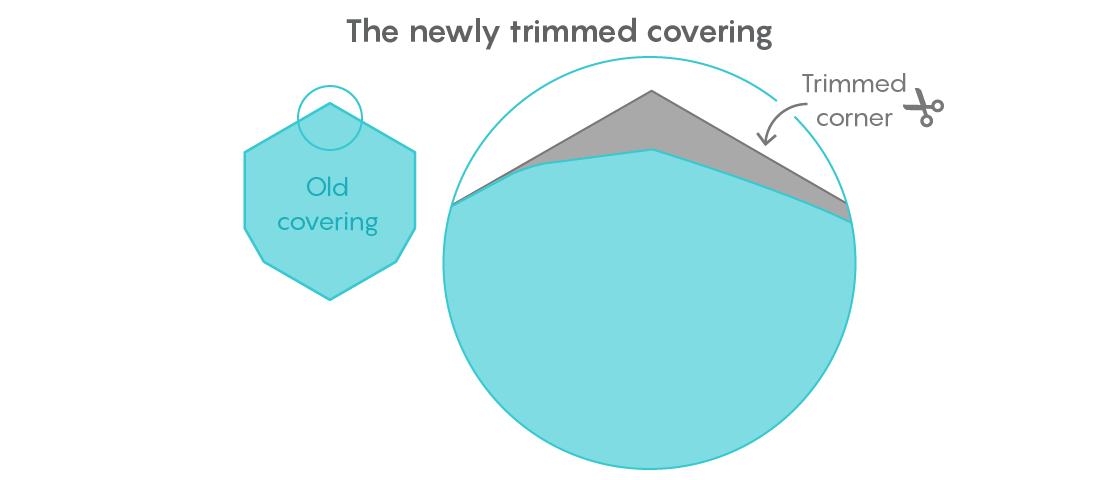
Sa stratégie était de déplacer toutes les formes d'un diamètre de 1 vers le coin du revêtement universel qu'il avait découvert il y a plusieurs années, puis de supprimer toute la zone restante du coin opposé. Mais une mesure précise de l'espace économisé s'est avérée difficile. Les techniques utilisées par Gibbs étaient basées sur la géométrie euclidienne, mais ont été exécutées avec une telle précision qui choquerait n'importe quel lycéen.

«Du point de vue des mathématiques, ce n'est que de la géométrie pour le lycée. Mais joué avec une tension fanatique » , a écrit Baez.

Jusqu'à présent, Gibbs détient la première place à la recherche de la plus petite couverture universelle, mais son prix est en danger. Gibbs pense qu'il est possible de trouver une couverture encore plus petite. Baez espère que l'attention portée par Gibbs au problème de Lebesgue stimule l'intérêt d'autres mathématiciens. Il est peut-être temps de laisser de côté la règle et la boussole et d'utiliser tout l'arsenal des mathématiques modernes.

«Il est possible que la bonne façon de résoudre cette énigme utilise des idées complètement différentes», a-t-il dit, «même si je n'ai aucune idée de ce que cela pourrait être.»