Perspective: MultiClet S1

Il est donc temps de parler de la prochaine génération de processeurs multicellulaires: MultiClet S1. Si c'est la première fois que vous en entendez parler, assurez-vous de consulter l'histoire et l'idéologie de l'architecture dans ces articles:

• "Un processeur multicellulaire, c'est quoi?"
• "Multiclet R1 - les premiers tests"
• "Compilateur C / C ++ basé sur LLVM pour processeurs multicellulaires: être ou ne pas être?"

Pour le moment, le nouveau processeur est en cours de développement, mais les premiers résultats sont déjà apparus et vous pouvez évaluer de quoi il sera capable.

Commençons par les plus grands changements: les fonctionnalités de base.

CARACTÉRISTIQUES

Il est prévu d'atteindre les indicateurs suivants:

1. Nombre d'alvéoles: 64
2. Processus technique: 28 nm
3. Fréquence d'horloge: 1,6 GHz
4. La taille de la mémoire sur la puce: 8 Mo
5. Surface cristalline: 40 mm ²
6. Consommation électrique: 6 W

Les chiffres réels seront annoncés sur la base des résultats des tests des échantillons fabriqués en 2019. En plus des caractéristiques de la puce elle-même, le processeur prendra en charge jusqu'à 16 Go de RAM standard DDR4 3200 MHz, bus PCI Express et PLL.

Il convient de noter que le processus de fabrication à 28 nm est la gamme la plus basse des ménages qui ne nécessite pas d'autorisations spéciales pour l'utilisation, c'est donc lui qui a été choisi. Par le nombre de cellules, différentes options ont été envisagées: 128 et 256, mais avec une augmentation de la surface du cristal, le pourcentage de rejets augmente. Nous nous sommes installés sur 64 cellules et, par conséquent, une zone relativement petite, ce qui donnera un plus grand rendement de cristaux appropriés sur la plaque. D'autres développements sont possibles dans le cadre de l' ICS (système dans le cas) , où il sera possible de combiner plusieurs cristaux à 64 cellules dans un cas.

Il faut dire que le but et l'utilisation du processeur changent radicalement. S1 ne sera pas un microprocesseur conçu pour l'intégration, comme l'ont été P1 et R1, mais un accélérateur de calculs. Tout comme GPGPU, une carte basée sur S1 peut être insérée dans la carte mère PCI Express d'un PC ordinaire et utilisée pour le traitement des données.

L'architecture

En S1, le «multicellule» est désormais l'unité de calcul minimale: un ensemble de 4 cellules exécutant une certaine séquence de commandes. Au début, il était prévu de combiner des multicellules en groupes appelés un cluster pour l'exécution conjointe de commandes: un cluster devait contenir 4 multicellules, au total il y avait 4 clusters séparés sur un cristal. Cependant, chaque cellule a une connexion complète avec toutes les autres cellules du cluster, et avec une augmentation du groupe de liaisons, elle devient trop importante, ce qui complique considérablement la conception topologique du microcircuit et réduit ses caractéristiques. Par conséquent, ils ont décidé d'abandonner la division en grappes, car la complication ne justifie pas les résultats. De plus, pour des performances maximales, il est plus avantageux d'exécuter du code en parallèle sur chaque multicellule. Total, maintenant le processeur contient 16 multicellules distinctes.

Une multicellule, bien qu'elle se compose de 4 cellules, diffère d'une R1 à 4 cellules, dans laquelle chaque cellule a sa propre mémoire, son propre bloc de commandes d'échantillons, sa propre ALU. S1 est arrangé un peu différemment. ALU comprend 2 parties: un bloc arithmétique à virgule flottante et un bloc arithmétique entier. Chaque cellule a un bloc entier séparé, mais il n'y a que deux blocs à virgule flottante dans une multicellule, et donc deux paires de cellules les divisent entre elles. Cela a été fait principalement pour réduire la surface du cristal: l'arithmétique à virgule flottante 64 bits, contrairement à l'arithmétique entière, prend beaucoup de place. Avoir une telle ALU sur chaque cellule s'est avéré être redondant: la récupération des commandes ne fournit pas de chargement ALU et elles sont inactives. Tout en réduisant le nombre de blocs ALU et en maintenant le rythme des exemples de commandes et de données, comme le montre la pratique, le temps total pour résoudre les problèmes ne change pratiquement pas ou change légèrement, et les blocs ALU sont entièrement chargés. De plus, l'arithmétique à virgule flottante n'est pas utilisée aussi souvent qu'avec l'entier.

Une vue schématique des blocs de processeurs R1 et S1 est présentée dans le schéma ci-dessous. Ici:

• CU (Control Unit) - unité de récupération d'instructions
• ALU _FX - unité arithmétique et logique d'arithmétique entière
• ALU _FP - Unité logique arithmétique d'arithmétique à virgule flottante
• DMS (Data Memory Scheduler) - unité de commande de mémoire de données
• DM - mémoire de données
• PMS (Program Memory Scheduler) - unité de commande de mémoire de programme
• PM - mémoire de programme

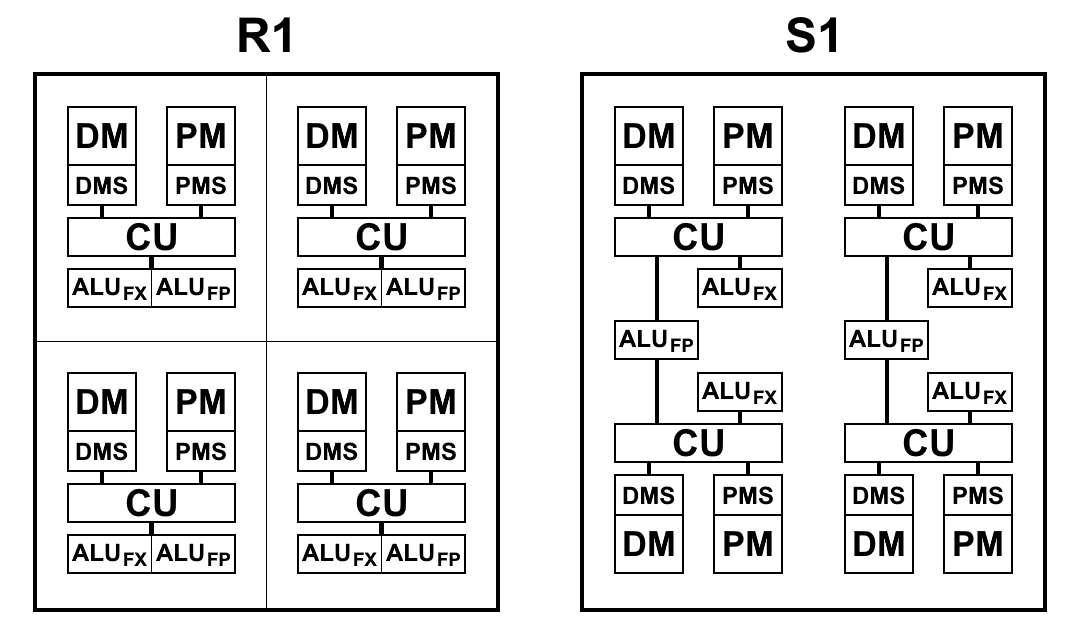
Différences architecturales S1:

1. Les équipes peuvent désormais accéder aux résultats des équipes des paragraphes précédents. Il s'agit d'un changement très important qui vous permet d'accélérer considérablement les transitions lors de la branche du code. Les processeurs P1 et R1 n'avaient d'autre choix que d'écrire les résultats souhaités dans la mémoire et de les relire immédiatement avec les toutes premières commandes du nouveau paragraphe. Même lors de l'utilisation de la mémoire sur une puce, les opérations d'écriture et de lecture prennent de 2 à 5 cycles chacune, ce qui peut être enregistré en se référant simplement au résultat de la commande du paragraphe précédent
2. L'écriture dans la mémoire et les registres se produit désormais immédiatement, et non à la fin d'un paragraphe, ce qui vous permet de commencer à écrire des commandes avant la fin du paragraphe. Par conséquent, les temps d'arrêt potentiels entre les paragraphes sont réduits.
3. Le système de commande a été optimisé, à savoir:
   
   • Ajout de l'arithmétique entière 64 bits: addition, soustraction, multiplication de nombres 32 bits, qui renvoie un résultat 64 bits.
   • La méthode de lecture à partir de la mémoire a été modifiée: désormais, pour toute commande, vous pouvez simplement spécifier l'adresse à partir de laquelle vous souhaitez lire les données comme argument, tandis que la séquence de commandes de lecture et d'écriture est préservée.
     
     Il a également rendu obsolète une commande de lecture de mémoire distincte. Au lieu de cela, la commande de valeur de chargement est utilisée dans le commutateur de chargement (précédemment, get ), en spécifiant l'adresse en mémoire comme argument:
     
     

     .data foo: .long 0x1234 .text habr: load_l foo ;      foo load_l [foo] ;    0x1234 add_l [foo], 0xABCD ;       ;   complete 

     
     
   • Un format de commande a été ajouté qui permet l'utilisation de 2 arguments constants.
     Auparavant, vous ne pouviez spécifier une constante que comme deuxième argument, le premier argument devrait toujours être un lien vers le résultat dans le commutateur. La modification s'applique à toutes les équipes à deux arguments. Le champ constant est toujours 32 bits, donc ce format permet, par exemple, de générer des constantes 64 bits avec une seule commande.
     
     C'était:
     
     

      load_l 0x12345678 patch_q @1, 0xDEADBEEF 

     
     C'est devenu:
     
     

      patch_q 0x12345678, 0xDEADBEEF 

     
     
   • Types de données vectorielles modifiées et complétées.
     Ce que l'on appelait autrefois les types de données «compactés» peut désormais être appelé en toute sécurité vectoriel. En P1 et R1, les opérations sur les nombres emballés ne prenaient qu'une constante comme deuxième argument, c'est-à-dire, par exemple, lors de l'ajout, chaque élément du vecteur était ajouté avec le même nombre, et cela ne pouvait pas être appliqué intelligemment. Maintenant, des opérations similaires peuvent être appliquées à deux vecteurs complets. De plus, cette façon de travailler avec des vecteurs est parfaitement cohérente avec le mécanisme des vecteurs dans LLVM, qui permet désormais au compilateur de générer du code à l'aide de types vectoriels.
     
     

      patch_q 0x00010002, 0x00030004 patch_q 0x00020003, 0x00040005 mul_ps @1, @2 ;  - 00020006000C0014 

     
     
   
   
4. Suppression des drapeaux du processeur.
   
   En conséquence, environ 40 équipes basées uniquement sur les valeurs des drapeaux ont été supprimées. Cela a considérablement réduit le nombre d'équipes et, par conséquent, la surface du cristal. Et toutes les informations nécessaires sont désormais stockées directement dans la cellule de commutation.
   
   
   • Lors de la comparaison avec zéro, au lieu du drapeau zéro, maintenant seule la valeur dans le commutateur est utilisée
   • Au lieu de l'indicateur de signe, un bit correspondant au type de commande est désormais utilisé: 7e pour l'octet, 15e pour le court, 31e pour le long, 63e pour le quad. Étant donné que le caractère se multiplie jusqu'au 63e bit, quel que soit le type, vous pouvez comparer des nombres de types différents:
     
     

      .data long: .long -0x1000 byte: .byte -0x10 .text habr: a := load_b [byte] ;     0xFFFFFFFFFFFFFFF0, ;   byte 7    63. b := loadu_b [byte] ;     0x00000000000000F0, ; ..  loadu_b    c := load_l [long] ;     0xFFFFFFFFFFFFF000. ge_l @a, @c ;   "  "  1: ;   31 ,   . lt_s @a, @b ; 1, .. b     complete 

     
     
   • L'indicateur de portage n'est plus nécessaire, car il existe une arithmétique 64 bits
   
   
5. Le temps de transition d'un paragraphe à l'autre a été réduit à 1 mesure (au lieu de 2-3 dans R1)

Compilateur basé sur LLVM

Le compilateur de langage C pour S1 est similaire à R1, et comme l'architecture n'a pas fondamentalement changé, les problèmes décrits dans l'article précédent n'ont malheureusement pas disparu.

Cependant, dans le processus de mise en œuvre du nouveau système de commande, la quantité de code de sortie a diminué d'elle-même, simplement en raison de la mise à jour du système de commande. En outre, il existe de nombreuses autres optimisations mineures qui réduiront le nombre d'instructions dans le code, dont certaines ont déjà été effectuées (par exemple, la génération de constantes 64 bits avec une seule instruction). Mais il y a des optimisations encore plus sérieuses qui doivent être faites, et elles peuvent être construites par ordre croissant d'efficacité et de complexité de mise en œuvre:

1. La possibilité de générer toutes les commandes à deux arguments avec deux constantes.
   
   La génération d'une constante 64 bits via patch_q n'est qu'un cas spécial, mais nous en avons besoin d'un général. En fait, le but de cette optimisation est de permettre aux équipes de remplacer uniquement le premier argument par une constante, car le deuxième argument pourrait toujours être une constante, et cela a longtemps été implémenté. Ce n'est pas un cas très fréquent, mais, par exemple, lorsque vous devez appeler une fonction et en écrire l'adresse de retour en haut de la pile, vous pouvez
   
   

    load_l func wr_l @1, #SP 

   
   optimiser pour
   
   

    wr_l func, #SP 

   
   
2. La possibilité de remplacer l'accès à la mémoire via un argument dans n'importe quelle commande.
   Par exemple, si vous devez ajouter deux nombres de la mémoire, vous pouvez
   
   

    load_l [foo] load_l [bar] add_l @1, @2 

   
   optimiser pour
   
   

    add_l [foo], [bar] 

   
   Cette optimisation est une extension de la précédente, cependant, une analyse est déjà nécessaire ici: un tel remplacement ne peut être effectué que si les valeurs chargées ne sont utilisées qu'une seule fois dans cette commande d'addition et nulle part ailleurs. Si le résultat de la lecture est utilisé même dans seulement deux commandes, il est plus avantageux de lire une fois dans la mémoire en tant que commande distincte, et dans les deux autres de s'y référer via le commutateur.
   
3. Optimisation du transfert des registres virtuels entre les unités de base.
   Pour R1, le transfert de tous les registres virtuels se faisait par la mémoire, ce qui donne lieu à un très grand nombre de lectures et d'écritures en mémoire, mais il n'y avait tout simplement pas d'autre moyen de transférer des données entre les paragraphes. S1 vous permet d'accéder aux résultats des commandes des paragraphes précédents, par conséquent, théoriquement, de nombreuses opérations de mémoire peuvent être supprimées, ce qui donnerait le plus grand effet parmi toutes les optimisations. Cependant, cette approche est encore limitée par le switch: pas plus de 63 résultats précédents, si loin de chaque transfert du registre virtuel, peuvent être implémentés comme ça. Comment procéder n'est pas une tâche triviale, et une analyse des possibilités de résolution reste à faire. Les sources du compilateur peuvent apparaître dans le domaine public, donc si quelqu'un a des idées et que vous souhaitez rejoindre le développement, vous pouvez le faire.
   

Repères

Le processeur n'étant pas encore sorti sur la puce, il est difficile d'évaluer ses performances réelles. Cependant, le code du noyau RTL est déjà prêt, ce qui signifie que vous pouvez effectuer une évaluation à l'aide de la simulation ou du FPGA. Pour exécuter les benchmarks suivants, nous avons utilisé une simulation à l'aide du programme ModelSim pour calculer le temps d'exécution exact (en mesures). Puisqu'il est difficile de simuler le cristal entier et que cela prend très longtemps, une multicellule a donc été simulée et le résultat a été multiplié par 16 (si la tâche est conçue pour le multithreading), car chaque multicellule peut fonctionner de manière complètement indépendante des autres.

Dans le même temps, une modélisation multicellulaire a été effectuée sur Xilinx Virtex-6 pour tester les performances du code processeur sur du matériel réel.

Coremark

CoreMark - un ensemble de tests pour une évaluation complète des performances des microcontrôleurs et des processeurs centraux, ainsi que de leurs compilateurs C. Comme vous pouvez le voir, le processeur S1 n'est ni l'un ni l'autre. Cependant, il est destiné à exécuter un code d'arbitrage absolu, c'est-à-dire toute personne pouvant s'exécuter sur le processeur central. CoreMark convient donc pour évaluer les performances de S1 pas pire.

CoreMark contient du travail avec des listes liées, des matrices, une machine d'état et un calcul de somme CRC . En général, la plupart du code se révèle être strictement séquentiel (qui teste le parallélisme matériel multicellulaire pour la force) et avec de nombreuses branches, c'est pourquoi les capacités du compilateur jouent un rôle important dans les performances finales. Le code compilé contient pas mal de courts paragraphes et malgré le fait que la vitesse de transition entre eux ait augmenté, la ramification inclut le travail avec la mémoire, ce que nous aimerions éviter au maximum.

Carte de performance CoreMark:

	Multiclet R1 (compilateur llvm)	Multiclet S1 (compilateur llvm)	Elbrus-4C (R500 / E)	Texas Inst. AM5728 ARM Cortex-A15	Baikal-t1	Intel Core i7 7700K
Année de fabrication	2015	2019	2014	2018	2016	2017
Fréquence d'horloge, MHz	100	1600	700	1500	1200	4500
Score global CoreMark	59	18356	1214	15789	13142	182128
Coremark / MHz	0,59	11,47	5,05	10,53	10,95	40,47

Le résultat d'une multicellule est 1147, ou 0,72 / MHz, ce qui est supérieur à celui de R1. Cela parle des avantages du développement d'une architecture multicellulaire dans le nouveau processeur.

Wheatstone

Whetstone - un ensemble de tests pour mesurer les performances du processeur lorsque vous travaillez avec des nombres à virgule flottante. Ici, la situation est bien meilleure: le code est également séquentiel, mais sans grand nombre de branches et avec une bonne concurrence interne.

Whetstone se compose de nombreux modules, ce qui vous permet de mesurer non seulement le résultat global, mais également les performances de chaque module spécifique:

1. Éléments du tableau
2. Tableau comme paramètre
3. Sauts conditionnels
4. Arithmétique entière
5. Fonctions trigonométriques (tan, sin, cos)
6. Appels de procédure
7. Références de tableau
8. Fonctions standard (sqrt, exp, log)

Ils sont divisés en catégories: les modules 1, 2 et 6 mesurent les performances des opérations en virgule flottante (lignes MFLOPS1-3); modules 5 et 8 - fonctions mathématiques (COS MOPS, EXP MOPS); modules 4 et 7 - arithmétique entière (FIXPT MOPS, EQUAL MOPS); module 3 - sauts conditionnels (IF MOPS). Dans le tableau ci-dessous, la deuxième ligne de MWIPS est un indicateur général.

Contrairement à CoreMark, Whetstone sera comparé sur un cœur ou, comme dans notre cas, sur une multicellule. Étant donné que le nombre de cœurs est très différent dans les différents processeurs, alors, pour la pureté de l'expérience, nous considérons les indicateurs par mégahertz.

Tableau de bord Whetstone:

CPU	MultiClet R1	MultiClet S1	Core i7 4820K	ARM v8-A53
Fréquence, MHz	100	1600	3900	1300
MWIPS / MHz	0,311	0,343	0,887	0,642
MFLOPS1 / MHz	0,157	0,156	0,341	0,268
MFLOPS2 / MHz	0,153	0,111	0,308	0,241
MFLOPS3 / MHz	0,029	0,124	0,167	0,239
COS MOPS / MHz	0,018	0,008	0,023	0,028
EXP MOPS / MHz	0,008	0,005	0,014	0,004
FIXPT MOPS / MHz	0,714	0,116	0,998	1,197
SI MOPS / MHz	0,081	0,196	1,504	1,436
EGAL MOPS / MHz	0,143	0,149	0,251	0,439

Whetstone contient des opérations de calcul beaucoup plus directement que CoreMark (ce qui est très visible en regardant le code ci-dessous), il est donc important de se rappeler ici: le nombre d'ALU à virgule flottante est divisé par deux. Cependant, la vitesse de calcul n'a presque pas été affectée, par rapport à R1.

Certains modules s'intègrent très bien sur une architecture multicellulaire. Par exemple, le module 2 compte beaucoup de valeurs dans un cycle, et grâce à la prise en charge complète des nombres à virgule flottante double précision par le processeur et le compilateur, après la compilation, nous obtenons de grands et beaux paragraphes qui révèlent vraiment les capacités de calcul d'une architecture multicellulaire:

popcnt

Pour refléter les caractéristiques de l'architecture elle-même (quel que soit le compilateur), nous mesurerons quelque chose écrit en assembleur en tenant compte de toutes les caractéristiques de l'architecture. Par exemple, compter des bits unitaires dans un nombre de 512 bits (popcnt). Pour des raisons d'évidence, nous prendrons les résultats d'une multicellule, afin qu'ils puissent être comparés à R1.

Tableau de comparaison, le nombre de cycles d'horloge par cycle de calcul 32 bits:

Algorithme	Multiclet r1	Multiclet S1 (une multicellule)
Bithacks	5,0	2,625

De nouvelles instructions vectorielles mises à jour ont été utilisées ici, ce qui nous a permis de réduire de moitié le nombre d'instructions par rapport au même algorithme implémenté dans l'assembleur R1. La vitesse de travail, respectivement, a augmenté de près de 2 fois.

Ethereum

Les repères sont, bien sûr, bons, mais nous avons une tâche spécifique: créer un accélérateur de calcul, et ce serait bien de savoir comment il gère les tâches du monde réel. Les crypto-monnaies modernes sont les mieux adaptées pour une telle vérification, car les algorithmes d'exploration de données fonctionnent sur de nombreux appareils différents et peuvent donc servir de référence pour la comparaison. Nous avons commencé avec Ethereum et l'algorithme Ethash, qui s'exécute directement sur le périphérique d'exploration de données.

Le choix d'Ethereum était dû aux considérations suivantes. Comme vous le savez, des algorithmes tels que Bitcoin sont très efficacement mis en œuvre par des puces ASIC spécialisées, de sorte que l'utilisation de processeurs ou de cartes vidéo pour extraire Bitcoin et ses clones devient économiquement désavantageuse en raison de faibles performances et d'une consommation d'énergie élevée. La communauté des mineurs, pour tenter de sortir de cette situation, développe des crypto-monnaies sur d'autres principes algorithmiques, en se concentrant sur le développement d'algorithmes qui utilisent des processeurs à usage général ou des cartes vidéo pour l'exploitation minière. Cette tendance devrait se poursuivre à l'avenir. Ethereum est la crypto-monnaie la plus célèbre basée sur cette approche. Le principal outil d'extraction d'Ethereum sont les cartes vidéo, qui en termes d'efficacité (hashrate / TDP) sont nettement (plusieurs fois) en avance sur les processeurs à usage général.

Ethash est un soi-disant algorithme lié à la mémoire , c'est-à-dire son temps de calcul est principalement limité par la quantité et la vitesse de la mémoire, et non par la vitesse des calculs eux-mêmes. Maintenant, pour l'exploitation minière Ethereum, les cartes vidéo sont les mieux adaptées, mais leur capacité à effectuer simultanément de nombreuses opérations n'aide pas beaucoup, et elles reposent toujours sur la vitesse de la RAM, ce qui est clairement démontré dans cet article . De là, vous pouvez prendre une photo illustrant le fonctionnement de l'algorithme pour expliquer pourquoi cela se produit.



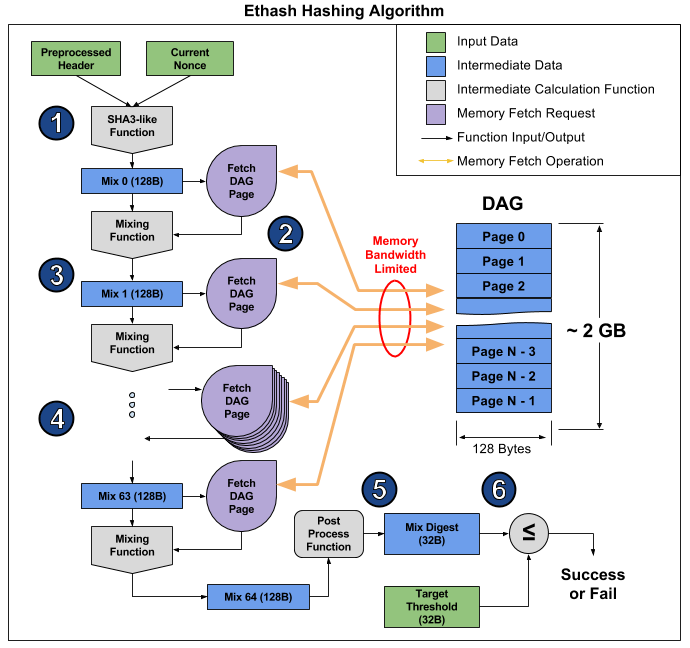
L'article décompose l'algorithme en 6 points, mais 3 étapes peuvent être distinguées pour encore plus d'évidence:

1. Début: SHA-3 (512) pour calculer le Mix 0 original de 128 octets (point 1)
2. Recalcul de 64 fois la matrice de mixage en lisant les 128 octets suivants et en les mélangeant avec les précédents via la fonction de mélange, pour un total de 8 kilo-octets (paragraphes 2 à 4)
3. Finalisation et vérification du résultat

La lecture de 128 octets aléatoires à partir de la RAM prend beaucoup plus de temps qu'il n'y paraît. Si vous prenez la carte graphique MSI RX 470, qui a 2048 appareils informatiques et une bande passante mémoire maximale de 211,2 Go / s, alors pour équiper chaque appareil, vous avez besoin de 1 / (211,2 Go / (128 b * 2048)) = 1241 ns, soit environ 1496 cycles à une fréquence donnée. Compte tenu de la taille de la fonction de mixage, on peut supposer qu'il faut plusieurs fois plus de temps pour lire la mémoire d'une carte vidéo que pour recalculer les informations reçues. En conséquence, l'étape 2 de l'algorithme prend beaucoup de temps, beaucoup plus longtemps que les étapes 1 et 3, qui au final ont peu d'effet sur les performances, malgré le fait qu'elles contiennent plus de calculs (principalement dans SHA-3). Vous pouvez simplement regarder le hashrate de cette carte vidéo: 26,375 méga-shashs / ​​s théorique (limité uniquement par la bande passante mémoire) contre 24 mégachehes / s réels, c'est-à-dire que les étapes 1 et 3 ne prennent que 10% du temps.

Sur S1, les 16 multicellules peuvent fonctionner en parallèle et sur un code différent. De plus, une RAM double canal sera installée, le long d'un canal pour 8 multicellules. À l'étape 2 de l'algorithme Ethash, notre plan est le suivant: une multicellule lit 128 octets dans la mémoire et commence à les recompter, puis la suivante lit la mémoire et les recomptes, et ainsi de suite jusqu'au 8, c'est-à-dire une multicellule, après avoir lu 128 octets de mémoire, dispose de 7 * [temps de lecture de 128 octets] pour recalculer le tableau. On suppose qu'une telle lecture prendra 16 cycles, c'est-à-dire 112 mesures sont données pour le recomptage. Le calcul de la fonction de mixage prend environ le même cycle d'horloge, donc S1 est proche du rapport idéal de la bande passante mémoire aux performances du processeur. Étant donné que le temps n'est pas perdu dans la deuxième étape, les parties restantes de l'algorithme doivent être optimisées autant que possible, car elles affectent vraiment les performances.

Pour évaluer la vitesse de calcul SHA-3 (Keccak), un programme C a été développé et testé, sur la base duquel sa version optimale en assembleur est en cours de création. La programmation d'évaluation montre qu'une multicellule effectue le calcul SHA-3 (Keccak) en 1550 cycles d'horloge. Par conséquent, le temps total pour calculer un hachage par multicellule sera de 1550 + 64 * (16 + 112) = 9742 cycles. Avec une fréquence de 1,6 GHz et 16 multicellules parallèles, le taux de hachage du processeur sera de 2,6 MHash / s.

Accélérateur	MultiClet S1	NVIDIA GeForce GTX 980 Ti	Radeon RX 470	Radeon RX Vega 64	NVIDIA GeForce GTX 1060	NVIDIA GeForce GTX 1080 Ti
Prix		650 $	180 $	500 $	300 $	700 $
Taux de hachage	2,6 MHash / s	21,6 MHash / s	25.8 MHash / s	43,5 MHash / s	25 MHash / s	55 MHash / s
TDP	6 W	250 W	120 W	295 W	120 W	250 W
Hashrate / TDP	0,43	0,09	0,22	0,15	0,22	0,21
Technologie de processus	28 nm	28 nm	14 nm	14 nm	16 nm	16 nm

Lorsque vous utilisez MultiClet S1 comme outil d'exploration de données, 20 processeurs ou plus peuvent en fait être installés sur les cartes. Dans ce cas, le hashrate d'une telle carte sera égal ou supérieur aux hashrates des cartes vidéo existantes, tandis que la consommation électrique d'une carte avec S1 sera moitié moins élevée, même que celle des cartes vidéo avec des normes topographiques de 16 et 14 nm.

En conclusion, je dois dire que la tâche principale est maintenant la fabrication d'une carte multiprocesseur pour un mineur de crypto-monnaie multicellulaire et un mineur de supercalculateur. La compétitivité devrait être atteinte en raison de la faible consommation d'énergie et de l'architecture, qui conviennent bien à l'informatique arbitraire.

Le processeur est toujours en développement, mais vous pouvez déjà commencer à programmer en langage assembleur, ainsi qu'évaluer la version actuelle du compilateur. Il existe déjà un SDK minimal contenant un assembleur, un éditeur de liens, un compilateur et un modèle fonctionnel, sur lequel vous pouvez démarrer et tester vos programmes.