Hé, piles complètes, entraînons les compétences. Je suggère de pétrir le gyrus, il me semble, il est intéressant de le faire en utilisant un paradigme différent et inhabituel. La plupart des développeurs ont développé une compétence d'algorithmisation - la tâche se transforme en briques qui doivent être connectées, pour réfléchir à la séquence de mouvements qui mène à la conclusion souhaitée.
Ici, il y a une semaine, le Prologue a été mentionné, je voudrais répondre que le langage Prolog est adapté pour résoudre des problèmes. J'ai déjà abordé ce sujet et cité plusieurs solutions de tâches aléatoires à ma disposition à partir d'un site avec des tâches pour les algorithmes , je voudrais montrer que toute solution complexe est disponible dans un langage déclaratif, et qu'elle ne peut pas fonctionner plus lentement (enfin, peut-être sensiblement pas très lent).
Il a fallu beaucoup de temps pour présenter le prochain problème, et la première solution a déjà été reçue, je démontre le problème et découvre à quel point il est lent.
Le prologue est intéressant en ce que vous pouvez créer un programme déductif qui montre beaucoup de solutions et peut même le limiter, mais ne fournit pas un moyen d'itérer,
l'algorithme sera développé solveur interprète.
Donc, la tâche est la suivante :
- Piéger l'eau de pluie ii
Étant donné une matrice mxn d'entiers positifs représentant la hauteur de chaque cellule unitaire dans une carte d'élévation 2D, calculez le volume d'eau qu'elle est capable de piéger après la pluie.
Remarque:
M et n sont tous deux inférieurs à 110. La hauteur de chaque cellule élémentaire est supérieure à 0 et inférieure à 20 000.
Exemple:
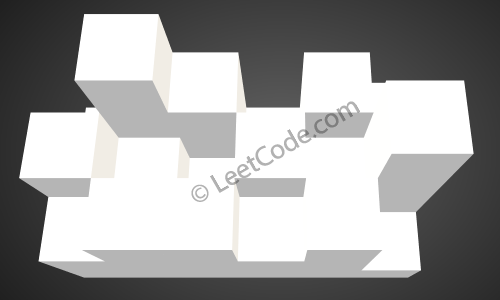
Étant donné la carte de hauteur 3x6 suivante:
[
[1,4,3,1,3,2],
[3,2,1,3,2,4],
[2,3,3,2,3,1]
]
Retour 4.
Après de longues tentatives pour formuler une solution, je suis arrivé à cette formulation:
Il est nécessaire de verser un maximum d'eau dans chaque cellule, qui ne se déverserait pas hors d'elle . Je suggère de verser une certaine quantité d'eau dans chaque cellule, mais pour qu'elle soit inférieure à la valeur maximale possible.
Il s'est avéré comme ceci:
reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!.
ce prédicat prend la liste d'entrée (matrice) et la transforme en solution, en matrice dans laquelle il y a d'autres valeurs qui seront une réponse valide. Ensuite, un autre prédicat prend ces deux listes élément par élément et trouve le montant total.
repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X).
ce prédicat prendra l'une des solutions, et vérifiera s'il est «normalement» rempli, s'il satisfait à l'état du problème, alors c'est la solution.
Il s'agit de la méthode "générer et vérifier", nous disons que la valeur est dans un tel ensemble et nous révisons tous les éléments de cet ensemble, vérifiant une sorte de condition de sortie.
Donc, j'obtiendrai une nouvelle solution avec le prédicat put (Vals, X0, X1), voici en premier lieu une liste de toutes les hauteurs possibles qui sont dans cette matrice, à partir de laquelle nous sélectionnerons les hauteurs possibles pour chaque cellule. Selon l'analyse des tests d'entrée, il a été découvert que dans ce problème, il est possible de remplir la cellule entière, si tant d'eau peut être insérée autour d'elle qu'elle est versée «sur la tête».
Au total, ce prédicat semble plus compliqué, il est nécessaire de traiter les triplets de lignes qui composent un carré 3x3 (oui, il n'y a pas de tableau dans le Prolog, mais il ressemble à la description des données d'entrée, et nous l'utilisons en programmation déclarative, vous ne connaissez peut-être pas les indices des éléments du tableau , il n'y a qu'une liste avec sa tête et sa queue, alors décrivez simplement un modèle qui correspond à la spécification d'entrée).
puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St).
C'est ainsi qu'il s'avère exprimer une dérivation de la matrice, à partir de laquelle vous pouvez prendre les trois premières (et plus) rangées, à partir desquelles, vous pouvez également sélectionner, de gauche à droite, des triplets d'éléments, et entre les huit voisins, il y aura une [Itaya] [Utaya] cellule du paysage. Avec l'aide de sel_biger (R2, V, R21) une nouvelle signification de cette cellule est faite.
Cette valeur peut être définie sur la cellule actuelle, elle peut être l'une des hauteurs possibles, et même la liste est triée par ordre décroissant, de sorte que la première sera la hauteur la plus élevée qui soit disponible, puis toute suivante:
sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X).
C'était une description d'un «générateur de décision», et ensuite vous devez vous assurer que la matrice obtenue, à partir des hauteurs arbitrairement remplies à chaque point, est similaire à la réponse que nous demandons.
Et il fallait trouver un tel état que l'eau se dépose dans les trous, je vais essayer de le dire ainsi:
de neuf valeurs d'un carré est trois par trois, au centre il devrait toujours y avoir une hauteur telle qu'elle ne contredit pas la carte d'entrée, de sorte que le changement d'équilibre qui était à l'origine dans ces cellules n'a pas été obtenu, s'il y avait une hauteur, alors il ne devrait pas y avoir de cellules au-dessus, même si tout va inonder d'eau, alors ici on peut dire que la cellule haute doit rester seule ou être remplacée par une valeur plus élevée, mais telle qu'elle soit égale à tous les voisins, c'est-à-dire les cellules à gauche, à droite et de haut en bas par rapport au courant doivent dépasser ou être égales, s'il y a plus d'eau dans la cellule, alors seulement si elle s'est élevée autour ...
Et les deux derniers prédicats, qui prennent la matrice d'entrée, démarrent la recherche d'un résultat approprié, soustraient la somme des éléments entre eux et trouvent la somme finale requise dans le problème:
diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. %% , sums(X,S):-reptest(X,X1),diffall(X,X1,S).
Je vais démontrer les tests que le site a fournis.
reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!. repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X). puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St). sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X). % balns([],[]). balns([_],[_]). balns([_,_],[_,_]). balns([B1,B2,B3|Tb],[R1,R2,R3|T]) :- blevel(B1,B2,B3,R1,R2,R3), balns([B2,B3|Tb],[R2,R3|T]). % , 33 blevel([],[],[],[],[],[]). blevel([_],[_],[_],[_],[_],[_]). blevel([_,_],[_,_],[_,_],[_,_],[_,_],[_,_]). blevel([_,U1,U2|Tu],[R,C,L|T],[_,B1,B2|Tb], [_,U10,U20|Tu0],[R0,C0,L0|T0],[_,B10,B20|Tb0]):- equ(C,[U1,L,R,B1],C0,[U10,L0,R0,B10]), blevel([U1,U2|Tu],[C,L|T],[B1,B2|Tb], [U10,U20|Tu0],[C0,L0|T0],[B10,B20|Tb0]). % , % equ(_,[],_,[]):-!. equ(C,_,C,_):-!. equ(C0,_,C,N):-C>C0,!,findall(X,(member(X,N),X<C),[]). equ(C0,[C0|T0],C,[C|T]):-!,equ(C0,T0,C,T). diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. sums(X,S):-reptest(X,X1),diffall(X,X1,S). %unit-tests framework assert_are_equal(Goal, false):-get_time(St),not(Goal),!,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, true):- get_time(St),Goal, !,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, Exp):-writeln(Goal->failed:expected-Exp). :-assert_are_equal(sums([[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[1,3,3,1,3,2],[3,2,1,3,2,3],[3,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[12,13,1,12],[13,4,13,12],[13,8,10,12],[12,13,12,12],[13,13,13,13]],14),true). :-assert_are_equal(sums([[2,3,4],[5,6,7],[8,9,10],[11,12,13],[14,15,16]],0),true). :-assert_are_equal(sums([],0),true). :-assert_are_equal(sums([[1]],0),true). :-assert_are_equal(sums([[2,3]],0),true). :-assert_are_equal(sums([[3],[2]],0),true). :-assert_are_equal(sums([[18,2,3],[4,5,6],[7,8,9]],0),true). :-assert_are_equal(sums([[3,5,5],[5,4,5],[5,5,5]],1),true). :-assert_are_equal(sums([[5,5,5,1],[5,1,1,5],[5,1,5,5],[5,2,5,8]],3),true). :-assert_are_equal(sums([[2,2,2],[2,1,2],[2,1,2],[2,1,2]],0),true). :-assert_are_equal(sums([[17,2,3,4,5,6,7,8,9,10]],0),true). :-assert_are_equal(sums([[9,9,9,9,9],[9,2,1,2,9],[9,2,8,2,9],[9,2,3,2,9],[9,9,9,9,9]],57),true). %:-assert_are_equal(sums([[9,9,9,9,9,9,8,9,9,9,9],[9,0,0,0,0,0,1,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,9,9,9,9,9,9,9,9,9,9]],215),true). :-assert_are_equal(sums([[11,21,31],[81,9,41],[17,61,51]],12),true). :-assert_are_equal(sums([[3,3,4,4,4,2],[3,1,3,2,1,4],[7,3,1,6,4,1]],5),true). %:-assert_are_equal(sums([[78,16,94,36],[87,93,50,22],[63,28,91,60],[64,27,41,27],[73,37,12,69],[68,30,83,31],[63,24,68,36]],44),true).
J'ai dû commenter les tests. tout n'est pas passé.
La tâche est de savoir comment l'accélérer?
Certaines solutions sont introuvables, en raison d'une longue recherche de solutions, elles sont générées trop lentement dans cet ordre, ici la complexité est probablement n!, Toutes les valeurs possibles pour chaque cellule du tableau sont triées.
Il est commode d'exprimer cette tâche dans un système de programmation dans des restrictions, juste au Prolog cela s'appelle comme ceci: CLP (FD): Programmation Logique de Contrainte sur des Domaines Finis.
clp (fd) est une bibliothèque incluse dans la distribution SWI-Prolog standard. Il résout les problèmes qui impliquent des ensembles de variables, où les relations entre les variables doivent être satisfaites.
>>
Je formule le problème comme ceci:
Nous avons besoin d'une telle liste, chaque élément de l'ensemble de valeurs supérieur ou égal à sa valeur maximale sur toute la carte, en tenant compte de la limitation selon laquelle les éléments doivent être situés clairement dans l'ordre du liquide déversé correspondant.
Voici comment je fais à partir de la liste d'entrée, une nouvelle liste dont les éléments sont devenus inconnus dans une plage donnée (de la valeur R2 de l'élément actuel à la valeur maximale de V)
En entrée, une liste de listes; en sortie, une nouvelle liste avec la distribution maximale des valeurs,
qui satisfont à la limitation des "bilans fluides":
checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St).
Il s'agit à la fois d'un générateur et d'un chèque à la fois, il est indiqué que les éléments sont dans un tel ensemble, puis en imposant progressivement un chèque, cet ensemble est rétréci. De plus, quelque chose reste, et il peut être "marqué", c'est-à-dire définir des valeurs entières qui satisferont la somme de toutes les contraintes. L'appel d' étiquetage ([bas], FX2) force à se remplir (contact) les variables inconnu avec des valeurs spécifiques, et il peut y avoir plusieurs de ces options, mais nous prendrons toujours la toute première, car il a été dit que toutes les variables se déplacent vers le bas dans la recherche, à partir de leurs limites supérieures, ce sont les options de recherche [vers le bas].
Et là, vous pouvez voir des paramètres complexes tels que:16.2.1. stratégie de sélection des variables
La stratégie de sélection des variables vous permet de spécifier quelle variable de Vars est étiquetée ensuite et est l'une des suivantes:
leftmost - Étiquetez les variables dans l'ordre dans lequel elles apparaissent à Vars. C'est la valeur par défaut.
ff Premier échec. Étiquetez ensuite la variable la plus à gauche avec le plus petit domaine, afin de détecter rapidement l'infaisabilité. Il s'agit souvent d'une bonne stratégie lorsqu'il existe de petits domaines pour les variables suivantes lorsqu'une première variable est choisie.
ffc Parmi les variables avec les plus petits domaines, la plus à gauche participant à la plupart des contraintes est étiquetée ensuite. L'application d'une contrainte doit supprimer un sous-arbre, ce qui peut donc être une bonne stratégie.
min Étiquette la variable la plus à gauche dont la limite inférieure est la plus basse suivante. notez qu'il s'agit de min / 0, différent de min / 1, qui détermine la solution en solution et est discuté dans la section précédente ci-dessus. C'est une bonne tactique si vous essayez de minimiser une valeur globale susceptible d'être inférieure si diverses variables le sont (par exemple une solution à coût minimum).
max Étiquetez la variable la plus à gauche dont la limite supérieure est la plus élevée suivante. Cela aussi est différent de max / 1. Et les conseils pour min s'appliquent à max lorsque vous essayez de maximiser une valeur globale.
16.2.2. ordre de valeur
L'ordre de valeur est l'un des suivants:
up Essayez les éléments du domaine de la variable choisie dans l'ordre croissant. C'est la valeur par défaut.
down Essayez les éléments du domaine dans l'ordre décroissant.
De toute évidence, si vous avez une distribution asymétrique, comme nous l'avons montré dans la façon d'étiqueter efficacement ci-dessus, essayez les éléments dans le premier ordre le plus courant.
16.2.3. stratégie de branchement
La stratégie de branchement est l'une des suivantes:
étape Pour chaque variable X, un choix est fait entre X = V et X # \ = V, où V est déterminé par les options de classement des valeurs. C'est la valeur par défaut.
enum Pour chaque variable X, un choix est fait entre X = V_1, X = V_2 etc., pour toutes les valeurs V_i du domaine de X. L'ordre est déterminé par les options de classement des valeurs.
bissect Pour chaque variable X, un choix est fait entre X # = <M et X #> M, où M est le milieu du domaine de X. Choisissez cette option si de nombreuses variables sont des sélections parmi une plage d'entiers, une valeur, plutôt qu'une parmi un ensemble de valeurs énumérées (par exemple des pourcentages, vs a = 0, b = 1, c = 2)
Maintenant, ce qui est «équilibré», c'est quand l'eau versée ne déborde pas de cellule en cellule. Il s'agit de la correspondance de l'ordre initial des éléments. Vous pourriez penser que le remplissage des cellules préservera la forme du paysage d'origine, ce qui signifie que s'il y avait un mur, il peut être recouvert d'eau par-dessus, de sorte qu'il devienne nécessairement égal à tous ses voisins, ou s'il ne s'agit pas d'un mur recouvert d'eau ...
Considérez les situations équilibrées:
-Si la cellule est inondée, alors à côté du même ou même plus haut (du coup c'est le mur).
- Si la cellule était égale à la voisine, alors elle devrait être égale à la nouvelle voisine.
-Et dans le cas extrême, la cellule n'a pas changé de sens, et encore quel genre de voisins elle avait:
C'est ainsi que vous pouvez transférer votre attitude envers la tâche dans le programme. Il n'est pas nécessaire pour moi de réfléchir à un algorithme de décision, il est important de fournir une description correcte du résultat, de définir correctement toutes les contraintes initiales (ensembles de valeurs). Cette approche peut simplement être «mélangée» avec la recherche habituelle avec retour et récursivité inhérente à Prolog. C'est un moyen de formuler des programmes encore plus déclaratifs que d'utiliser les méthodes Prolog classiques.
Je donnerai la solution obtenue, avec un ensemble de tests:
:- use_module(library(clpfd)). checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St).
Et plus de tests :-assert_are_equal(sums([[13,16,15,18,15,15],[14,1,8,9,7,9],[19,5,4,2,5,10],[13,1,7,9,10,3],[17,7,5,10,6,1],[15,9,8,2,8,3]],36),true). :-assert_are_equal(sums([[18,13,13,17,12,11],[17,2,6,10,5,10],[11,10,2,8,8,2],[12,6,10,8,8,7],[18,4,7,6,7,4],[20,5,9,2,3,10]],18),true). :-assert_are_equal(sums([[14,20,11,19,19,16],[11,10,7,4,9,6],[17,2,2,6,10,9],[15,9,2,1,4,1],[15,5,5,5,8,7],[14,2,8,6,10,7]],11),true). :-assert_are_equal(sums([[19383,10886,12777,16915,17793,18335,15386,10492,16649,11421],[12362,27,8690,59,7763,3926,540,3426,9172,5736],[15211,5368,2567,6429,5782,1530,2862,5123,4067,3135],[13929,9802,4022,3058,3069,8167,1393,8456,5011,8042],[16229,7373,4421,4919,3784,8537,5198,4324,8315,4370],[16413,3526,6091,8980,9956,1873,6862,9170,6996,7281],[12305,925,7084,6327,336,6505,846,1729,1313,5857],[16124,3895,9582,545,8814,3367,5434,364,4043,3750],[11087,6808,7276,7178,5788,3584,5403,2651,2754,2399],[19932,5060,9676,3368,7739,12,6226,8586,8094,7539]],79058),true). :-assert_are_equal(sums([[10795,10570,11434,10378,17467,16601,10097,12902,13317,10492],[16652,756,7301,280,4286,9441,3865,9689,8444,6619],[18440,4729,8031,8117,8097,5771,4481,675,709,8927],[14567,7856,9497,2353,4586,6965,5306,4683,6219,8624],[11528,2871,5732,8829,9503,19,8270,3368,9708,6715],[16340,8149,7796,723,2618,2245,2846,3451,2921,3555],[12379,7488,7764,8228,9841,2350,5193,1500,7034,7764],[10124,4914,6987,5856,3743,6491,2227,8365,9859,1936],[11432,2551,6437,9228,3275,5407,1474,6121,8858,4395],[16029,1237,8235,3793,5818,4428,6143,1011,5928,9529]],68900),true). :-assert_are_equal(sums([[18776,12404,14443,15763,14613,14538,18606,16840,12904,14818],[15128,688,7369,7917,9917,6996,3324,7743,9470,2183],[18490,5499,9772,6725,5644,5590,7505,8139,2954,9786],[17669,8082,8542,8464,197,9507,9355,8804,6348,8611],[13622,7828,9299,7343,5746,5568,4340,5422,3311,3810],[17605,1801,5661,3730,4878,1305,9320,8736,9444,8626],[18522,3465,6708,3416,8282,3258,2924,7637,2062,5624],[12600,2036,3452,1899,9379,5550,7468,71,973,7131],[13881,4930,8933,5894,8660,163,7199,7981,8899,2996],[12959,3773,2813,9668,7190,1095,2926,6466,5084,1340]],61413),true). :-assert_are_equal(sums([[12090,17684,13376,15542,15936,19107,17445,19756,19179,18418],[16887,9412,3348,2172,1659,2009,2336,5210,6342,7587],[18206,9301,7713,7372,5321,1255,4819,4599,7721,9904],[15939,9811,3940,5667,1705,6228,1127,9150,5984,6658],[13920,9224,2422,7269,1396,4081,5630,84,9292,1972],[17672,3850,7625,5385,1222,9299,6640,6042,3898,713],[12298,6190,524,2590,8209,8581,8819,9336,7732,1155],[15994,8004,379,4769,5273,1776,8850,7255,1860,8142],[15579,5884,1993,3205,7621,9567,2504,613,1961,2754],[11326,4259,8944,8202,3202,3506,6784,2021,2842,868]],89383),true). :-assert_are_equal(sums([[19528,15189,18872,19908,19958,10498,18036,18808,17753,16248],[13303,3333,2133,1648,2890,9754,7567,1746,368,9529],[14500,8046,3788,9797,6249,6990,3303,3033,5363,2497],[10253,4892,7686,9125,1152,3996,5975,9188,9157,3729],[15436,2460,3414,3921,460,6304,28,8027,8050,6748],[17556,8902,4794,7697,8699,1043,1039,2002,428,6403],[14500,681,7647,8538,6159,5151,2535,2134,4339,1692],[12215,6127,504,5629,49,964,8285,6429,5343,6335],[13177,2900,5238,7971,6949,289,5367,7988,2292,5795],[10743,3144,2829,8390,1682,5340,3541,569,3826,4232]],100439),true).
Ce sont des tests du site, seulement les 30 premières pièces. Le résultat est excellent, le problème est résolu, et même rapidement, tout le temps jusqu'à une seconde.
Vous pouvez vérifier ...
En conclusion
La programmation déclarative implique une formalisation détaillée de la tâche, et le solveur recherchera la solution la plus efficace qui satisfera aux conditions.
Un peu plus loin dans le sujet, vous pouvez ouvrir minizinc , un langage de programmation dans lequel ce paradigme est intégré. Ils ont formulé de nombreuses significations, indiqué des restrictions et le tour est joué, la réponse. Ils résolvent le Sudoku , les tâches de coloration de la carte, le travail de planification , les problèmes de ressources, la planification. Je suggère de m'entraîner ...