Les mathématiques dans Gamedev sont simples. Triangulation et Triangle.Net dans Unity

Bonjour à tous! Je m'appelle Grisha et je suis le fondateur de CGDevs. Les mathématiques sont un outil très cool lors du développement de jeux. Mais si nous disons que c'est difficile à gérer sans comprendre les vecteurs et les matrices , alors les algorithmes de triangulation ne sont pas une chose si nécessaire, mais avec eux un assez grand nombre de problèmes intéressants sont résolus. Aujourd'hui, je voudrais parler d'un outil assez important en géométrie computationnelle, comme les triangulations et leur application dans l'industrie du jeu. De plus, j'ai écrit un port et quelques wrappers pour l'excellente bibliothèque Triangle.Net pour Unity. Si vous êtes intéressé - bienvenue au chat. Lien vers github attaché.

Qu'est-ce que la triangulation?

Dans le cas général, la triangulation est une partition d'un objet géométrique en triangles. Ce concept en soi est assez simple. Un exemple de base de triangulation dans le cas des moteurs de jeu est un maillage. À strictement parler, un maillage peut être composé non seulement de triangles, mais dans les moteurs de jeu pour diverses raisons, ce sont des maillages constitués de triangles qui sont pris.



Les triangulations sont différentes, mais l'un des types de triangulations les plus populaires est la triangulation de Delaunay. Ce type de triangulation se distingue par la propriété que dans le cercle circonscrit autour de chaque triangle, seuls se trouvent les sommets de ce triangle.

Pourquoi sont-ils nécessaires?

En général, en dehors de l'industrie du jeu, un grand nombre de tâches sont résolues à l'aide de triangulations. Dans le développement de jeux, la première tâche qui me vient à l'esprit est le maillage de navigation. Navmesh est une structure de données qui détermine la quantité d'espace qu'un joueur peut parcourir. Il évite des tâches de calcul complexes telles que la détermination des collisions avec une partie de l'environnement.

Le deuxième problème intéressant qui peut être résolu en utilisant la triangulation de Delaunay dans le développement de jeux est la génération de terrains et d'objets représentés comme un ensemble de points. Le principal avantage de la triangulation de Delaunay dans ce cas est que, sur la base de ses propriétés, elle permet d'éviter les triangles très pointus qui interfèrent et créent des artefacts sur le tirrain.



De plus, en utilisant la triangulation Delaunay contrainte et des algorithmes tels que le deuxième algorithme de Chew et l'algorithme de Ruppert, vous pouvez générer des maillages encore meilleurs pour les tirrains et générer de bons maillages pour une autre application - la méthode des éléments finis.

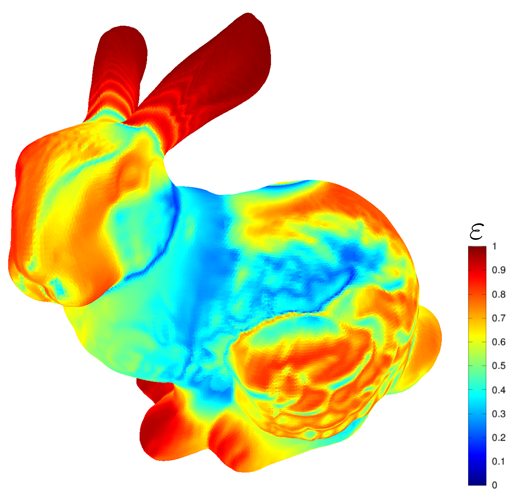
La méthode des éléments finis elle-même est l'une des méthodes par lesquelles les problèmes de physique appliquée sont résolus. Dans gamedev, il vous permet de résoudre de nombreux problèmes liés à la simulation de déformations, simulations de fluides et autres utilisées pour les spéciaux. les effets. Habituellement pour enregistrer des effets en animation, car en temps réel la méthode a une complexité de calcul trop élevée. Un détail important lors de l'utilisation de la méthode est que l'erreur de la méthode dépend des angles des triangles dans la grille. S'il y a des angles très nets dans la grille, la méthode donne une énorme erreur, pour cette raison les algorithmes listés ci-dessus sont nécessaires.



Et bien sûr, en général, la génération de maillage procédural. Par exemple, un projet github montre une scène avec la possibilité de dessiner des maillages. Certains puzzles physiques utilisent cette application comme mécanique de base. Mais en plus, les algorithmes de triangulation permettent d'utiliser la génération procédurale pour résoudre des problèmes tels que la destructibilité procédurale et ainsi de suite.

En plus des triangulations gamedev sont utilisées dans les réseaux, la vision par ordinateur, divers algorithmes analytiques, ainsi que dans quels problèmes de géométrie informatique, tels que la combinaison et l'élimination des polygones les uns des autres (ce qui est souvent utile dans les problèmes survenant lors du développement de jeux)

Coupure d'oreille avec trous

Peut-être l'un des algorithmes de triangulation les plus simples. Il ne donne pas la meilleure grille et a la plus grande complexité de calcul O (n ^ 2) dans le pire des cas.

Vous pouvez en savoir plus à ce sujet dans cet article.

Algorithme de Bowyer - Watson

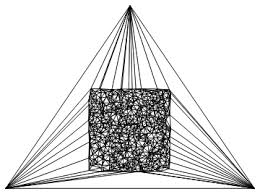
Un algorithme qui génère une triangulation de Delaunay sur un ensemble de points. En général, comme avec la plupart des algorithmes de Delaunay, s'ils sont correctement mis en œuvre, la complexité algorithmique est O (n log n), où n est le nombre de sommets. Mais dans certains cas, cela peut prendre O (n ^ 2).

Les inconvénients concernant l'écrêtage d'oreille sont que cet algorithme crée une triangulation convexe et dans l'implémentation de base n'implique pas de trous dans la grille résultante.

Traitement de raffinement Delaunay

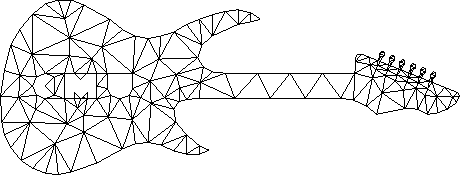
Le deuxième algorithme de Chew et l'algorithme de Ruppert sont des algorithmes qui vous permettent d'entrer des contraintes dans la triangulation de Delaunay et de définir l'angle minimum du triangle dans la grille. Un détail important des algorithmes est qu'ils peuvent entrer dans une boucle infinie et sont garantis pour donner des résultats à des angles compris entre environ 20,7 degrés et 29 degrés. La capacité de définir un angle minimum est importante pour résoudre les problèmes décrits ci-dessus.

Le deuxième algorithme de Chew est implémenté dans le package gratuit www.cs.cmu.edu/~quake/triangle.html et son port sur .Net archive.codeplex.com/?p=triangle

Triangle.Net pour Unity

Eh bien, comme à l'aide de triangulations, vous pouvez résoudre tant de tâches intéressantes, pendant les vacances, je voulais implémenter mon wrapper pour Unity, de sorte que j'ai toujours un outil pratique à portée de main. Dans cette implémentation, l'algorithme de triangulation fonctionne en moyenne pour O (n), et dans le pire des cas pour O (n * log n), où n est le nombre de sommets. Par exemple, lors du test de sommets de 1kk dispersés de manière aléatoire sur un carré, les unités de l'éditeur sur Intel Core i7-8700 ont construit une grille en 7,56 secondes en moyenne.

Les principales différences par rapport à la bibliothèque d'origine en présence de méthodes d'extension adaptées à Unity, ainsi que le remplacement de double par float dans toute la bibliothèque (+ quelques opérateurs spécifiques pour le casting) Double dans l'unité, n'a pas beaucoup de sens. Si nous considérons les simulations physiques, j'utiliserais une application distincte sur une bibliothèque plus, et le résultat des calculs a déjà donné Unity uniquement pour la visualisation. Et aussi renommé le type de maillage en TriangleNetMesh afin de ne pas renverser par rapport au maillage de Unity. Oui, ils sont déjà dans des espaces de noms différents, mais néanmoins, je pense que les nouveaux arrivants seraient un peu renversés par le fait qu'avec l'aide d'un Mesh, nous en obtenons un autre.

L'essence de la bibliothèque est que vous devez d'abord spécifier le soi-disant polygone. Ensuite, en fonction de cela, générez déjà le maillage. Pour que cela fonctionne avec les structures de données unitaires, plusieurs méthodes d'extension ont été introduites.



Pour l'exemple de démonstration et d'utilisation, une scène de démonstration spéciale a été créée avec la possibilité de dessiner des maillages. Vous pouvez vous familiariser avec lui et le port de la bibliothèque dans le projet github.

Merci de votre attention! J'espère que le portage et l'article seront utiles à quelqu'un et qu'il deviendra un peu plus clair pourquoi la triangulation et la connaissance des mathématiques dans leur ensemble sont nécessaires. Je vais essayer de continuer à divulguer des applications et des méthodes pour résoudre divers problèmes mathématiques dans le développement de jeux. Dans la géométrie informatique elle-même, il y a encore beaucoup de choses intéressantes, mais en plus il y a encore beaucoup d'autres sections intéressantes de mathématiques supérieures.