Prévision à nouveau, partie 1

Envisagez de prévoir des séries chronologiques. Essayons de prédire les graphiques de cotations, ou autre chose qui s'avère pratique.



Prenons comme base les prévisions présentées dans l'article Le modèle de prévision des séries chronologiques pour l'échantillon de similarité maximale: explication et exemple (cet article n'est pas le mien). Le bref point est que le segment le plus similaire du graphique à gauche de la prévision parmi l'historique du passé est recherché, puis les valeurs à droite du graphique sont prises à partir de cet ancien meilleur et utilisées comme prévisions.

J'irai plus loin. Lors du calcul des prévisions, je prendrai non pas un cas qui soit le meilleur en corrélation, mais un paquet des meilleurs. Et la prévision sera la moyenne des résultats de ce pack. Cela permettra de comprendre que la valeur trouvée est une régularité, et non une coïncidence accidentelle avec la prévision souhaitée, ou une déviation aléatoire si la prévision s'écarte de la prévision réelle.

Utiliser la meilleure option unique comme dans cet article n'est pas correct, ainsi que déterminer la distribution de probabilité avec une valeur à partir de cette distribution. Si vous générez un très grand graphique de données aléatoires et lancez une recherche sur celles-ci, il y aura certainement des segments en corrélation, et même éventuellement avec un coefficient de 0,9999, mais il n'est pas du tout nécessaire que des segments similaires continuent de suivre ces segments - c'est toujours tout est aléatoire. Et vous devez prendre juste un pack de ces segments et calculer que la variance des données suivantes est inférieure à la variance formée à partir d'un échantillon aléatoire de ces données. Et si la dispersion du pack est plus faible - alors c'est la prévision. Bien que ce ne soit pas non plus une représentation précise des erreurs possibles, cela suffit pour l'instant.

C'est-à-dire la prévision n'est pas le principe d'échantillonnage et de corrélation des segments comparés que nous utilisons, l'essentiel est qu'en raison de l'application de cet échantillon, la variance des valeurs souhaitées serait inférieure à celle résultant d'un échantillonnage aléatoire.

De plus, la variance de ce pack permettra d'évaluer lequel est préférable d'utiliser l'option de sélection des cas précédents. Après tout, il est possible de sélectionner pas toujours un segment de données en corrélation et de ne pas toujours utiliser la corrélation de Pearson. Et un tel choix peut être fait séparément pour chaque point prévu. Pour quel type d'échantillon la variance est moindre, cette option est meilleure pour le point actuel.

Quelle taille de pack devrait être? Cela repose sur la question des intervalles de confiance. Afin de ne pas trop charger, il est mentionné qu'il est préférable de prendre au moins 30 exemples pour déterminer la valeur moyenne. S'il y a un excès de données de test, j'en prendrais au moins 100.

Le rapport des écarts-types de l'échantillon selon l'algorithme et l'aléatoire peut être appelé le coefficient théorique de réussite de l'algorithme de prévision pour le point courant à des fins de comparaison avec d'autres algorithmes d'échantillonnage, ou pour déterminer l'utilité de cette prévision en général, alors que la valeur réelle n'est pas encore disponible.



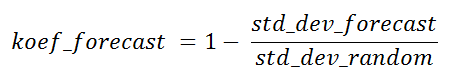
Ce coefficient peut dans certains cas prendre des valeurs négatives. Les points auxquels cela se produit sont de peu d'intérêt, tout comme les points avec un coefficient nul. Dans le cas d'une prévisibilité de 100%, elle sera égale à un.

Passons à des exemples pratiques, encore une fois à partir de cet article. Après avoir corrigé les petites erreurs, nous obtenons le résultat suivant, cohérent avec cet article et cet algorithme:

calcul des prévisions au 01/09/2012 23:00 position 52631
valeurs totales vérifiées pour la similitude 2184
la meilleure corrélation 0,958174 position 52295
coefficients de transfert alpha (1/2) 1.03117 -11.1992
erreur de prévision de fait mape 5.210%

mape - un terme de l'article original Erreur de pourcentage absolu moyen, calculé par la formule
Abs (Prévision - Fait) / Fait

Et maintenant, faisons une sélection non pas d'une meilleure similitude, mais de packs des meilleurs et de tout pour prédire un instant dans le temps et voir ce qui se passe:

0 corr 0.958174 pos 52295 mape 5.210%
1 corr 0.953571 pos 52151 mape 6.566%
2 corr 0.953532 pos 45599 mape 11.642%
3 corr 0.951462 pos 45743 mape 7.033%
4 corr 0.950921 pos 45575 mape 3.300%
5 corr 0.950789 pos 38687 mape 3.538%

La valeur de corrélation change ici de valeur en valeur négligeable. Dans le même temps, la valeur du résultat prévisionnel varie de 3% à 11%. C'est-à-dire que les 5% initiaux ne sont rien de plus qu'une coïncidence, ils pourraient être de 11% et 3%.

Dans les conditions de similitude spécifiées dans cet article, 2184 valeurs peuvent être comparées au total. Parmi ceux-ci, j'ai pris un pack des meilleurs en 1500 pièces, triés dans l'ordre de corrélation décroissante, et affiché dans un graphique. La corrélation dans ce pack des meilleurs 0,958 est tombée à 0,715 de gauche à droite. Mais la fluctuation du résultat n'a pratiquement pas changé:



On voit que la dépendance du résultat à la corrélation est très faible, mais elle semble néanmoins y être. En général, nous prenons un pack des 100 premières valeurs et calculons les prévisions, comme je l'ai mentionné, par la moyenne de ce pack. Le résultat est le suivant: mape 5,824%, stddev mape 7,035% . Mais ce 5,8% n'est plus une coïncidence, mais la moyenne de la distribution - la prévision la plus probable. L'écart type de mape est plus grand que le mape lui-même, mais c'est parce que le mape a une distribution non symétrique.

J'ai également calculé la même prévision mais en utilisant un échantillon conditionnellement aléatoire, plus précisément, simplement en moyenne à partir de toutes les options possibles, le résultat de mape était de 8,246% . Par échantillonnage aléatoire, l'erreur est légèrement plus grande, mais cette valeur est toujours dans la plage de la dispersion calculée à partir du meilleur échantillon. Pour le point calculé, le coefficient de prévision théorique indiqué par moi est proche de zéro, plus précisément koef_forecast = -0.041 . Je ne l'ai pas compté à partir de stddev mape (il comprend les prévisions réelles), mais à partir des valeurs absolues des prévisions, si vous regardez le programme, les chiffres originaux y sont donnés.

Mais c'est le cas en ce qui concerne l'horodatage, qui a été mentionné dans l'article d'origine. Mais si nous prenons par exemple «9/4/2012 23:00» (heure mois / jour / année), alors le coefficient d'efficacité théorique est koef_forecast = 0,21 , et mape = 3,126%, mape_rand = 7,147% . C'est-à-dire koef_forecast a montré à l'avance que le point actuel sera calculé plus précisément que le précédent. L'essence de l'utilité de ce coefficient est que vous pouvez au moins en quelque sorte évaluer le résultat avant même d'obtenir les données réelles, car les données réelles n'y participent pas. Plus il est haut, mieux c'est. J'ai déjà mentionné qu'un point absolument prédit aura un coefficient de un.

Vous pouvez voir vous-même comment tous ces chiffres changent dans mon programme de démonstration sur Qt C ++, là vous pouvez choisir la date et la taille du pack: les sources sur github

Les meilleures valeurs sont sélectionnées selon l'algorithme suivant:

inline void OrdPack::add_value(double koef, int i_pos) { if (std::isfinite(koef)==false) return; if (koef <= 0.0) return; if (mmap_ord.size() < ma_count_for_pack) { if (mmap_ord.size()==0) mi_koef = koef; mi_koef = std::min(mi_koef, koef); mmap_ord.insert({-koef,i_pos}); } else if (koef > mi_koef) { mmap_ord.insert({-koef,i_pos}); while (mmap_ord.size() > ma_count_for_pack) mmap_ord.erase(--mmap_ord.end()); mi_koef = -(--mmap_ord.end())->first; } } 

Il ne sert à rien de publier toute la source ici, ce n'est pas compliqué là-bas, et avec des commentaires. La base de la procédure MainWindow :: to_do_test () dans le fichier mainwindow.cpp .

Pour l'instant, je continuerai d'essayer de prédire quelque chose dans la prochaine partie.

PS. Veuillez laisser vos commentaires pour savoir si tout est clair sur ce qui manque. J'ai déjà établi un plan approximatif pour ce que j'écrirai ensuite, mais avec vos commentaires, je le ferai mieux.