Théorie du bonheur. La statistique comme moyen scientifique de ne rien savoir

Je continue de familiariser les lecteurs de Habr avec les chapitres de son livre "Theory of Happiness" avec le sous-titre "Mathematical Foundations of the Laws of Meanness". Ce livre de science populaire n'est pas encore publié, racontant de manière très informelle comment les mathématiques vous permettent de regarder le monde et la vie des gens avec un nouveau degré de conscience. C'est pour ceux qui s'intéressent à la science et pour ceux qui s'intéressent à la vie. Et puisque notre vie est complexe et, dans l'ensemble, imprévisible, l'accent dans le livre est principalement sur la théorie des probabilités et les statistiques mathématiques. Ici les théorèmes ne sont pas prouvés et les fondements de la science ne sont pas donnés, ce n'est en aucun cas un manuel, mais ce qu'on appelle la science récréative. Mais c'est précisément une telle approche presque ludique qui nous permet de développer l'intuition, d'égayer les cours pour les étudiants avec des exemples vivants et, enfin, d'expliquer aux non-mathématiciens et à nos enfants ce que nous avons trouvé si intéressant dans notre science sèche.


Ce chapitre traite des statistiques, de la météo et même de la philosophie. Ne vous inquiétez pas, juste un peu. Pas plus que ce qui peut être utilisé pour tabletalk dans une société décente.

Les chiffres sont trompeurs, surtout quand je les fais moi-même; à cette occasion, la déclaration attribuée à Disraeli est vraie: "Il existe trois types de mensonges: les mensonges, les mensonges flagrants et les statistiques".
Mark Twain

Combien de fois en été, nous prévoyons d'aller à l'extérieur, faire une promenade dans le parc ou faire un pique-nique, puis la pluie rompt nos plans, nous emprisonnant dans la maison! Et bien, si cela arrivait une ou deux fois par saison, il semble parfois que la météo suit le week-end, se rendant encore et encore samedi ou dimanche!

Un article relativement récent a été publié par des chercheurs australiens: "Les cycles hebdomadaires de température maximale et l'intensité des îles thermales urbaines." Elle a été reprise par les médias et a réimprimé les résultats avec le titre suivant: «Ne pensez-vous pas! Les scientifiques ont découvert que le temps le week-end est vraiment pire que les jours de semaine. » L'article cité fournit des statistiques sur la température et les précipitations sur plusieurs années dans plusieurs villes d'Australie et révèle en effet une baisse de la température de certaines heures du samedi et du dimanche. Après cela, une explication est donnée qui relie la météo locale au niveau de pollution de l'air en raison de l'augmentation du flux de trafic. Peu avant cela, une étude similaire a été menée en Allemagne et a conduit à peu près aux mêmes conclusions.

D'accord, les fractions de diplôme sont un effet très subtil. Se plaindre du mauvais temps le samedi tant attendu, nous discutons si la journée était ensoleillée ou pluvieuse, ce fait est plus facile à enregistrer, et plus tard à retenir, sans même avoir des instruments précis. Nous allons mener notre propre petite étude sur ce sujet et obtenir un résultat merveilleux: nous pouvons dire avec confiance que nous ne savons pas si le jour de la semaine et la météo sont liés au Kamchatka. Les études avec un résultat négatif ne tombent généralement pas sur les pages des magazines et dans les flux d'actualités, mais il est important pour vous et moi de comprendre sur quelle base, en général, je peux dire en toute confiance quelque chose au sujet des processus aléatoires. Et à cet égard, un résultat négatif n'est pas pire qu'un résultat positif.

Un mot pour défendre les statistiques

La statistique est blâmée pour la masse des péchés: dans les mensonges et dans les possibilités de manipulation et, enfin, dans l'incompréhensibilité. Mais je veux vraiment réhabiliter ce domaine de connaissances, montrer à quel point la tâche à laquelle elle est destinée est difficile et à quel point il est difficile de comprendre la réponse donnée par les statistiques.

La théorie des probabilités utilise une connaissance précise des variables aléatoires sous forme de distributions ou de calculs combinatoires complets. Je souligne encore une fois qu'il est possible d'avoir une connaissance précise d'une variable aléatoire. Mais que se passe-t-il si cette connaissance exacte nous est inaccessible et que la seule chose dont nous disposons est l'observation? Le développeur du nouveau médicament a un nombre limité de tests, le créateur du système de contrôle de la circulation n'a qu'une série de mesures sur la route réelle, le sociologue a les résultats des enquêtes, de plus, il peut être sûr qu'en répondant à certaines questions, les répondants vient de mentir.

Il est clair qu'une observation ne donne rien du tout. Deux - un peu plus que rien, trois, quatre ... cent ... combien d'observations avez-vous besoin pour avoir une connaissance d'une variable aléatoire dont vous pouvez être sûr avec une précision mathématique? Et quel genre de connaissances sera-ce? Très probablement, il sera présenté sous la forme d'un tableau ou d'un histogramme qui permet d'évaluer certains paramètres d'une variable aléatoire; ils sont appelés statistiques (par exemple, domaine de définition, moyenne ou variance, asymétrie, etc.). Peut-être qu'en regardant l'histogramme, on pourra deviner la forme exacte de la distribution. Mais attention! - tous les résultats d'observation eux-mêmes seront des variables aléatoires! Tant que nous n'avons pas une connaissance précise de la distribution, tous les résultats d'observation ne nous donnent qu'une description probabiliste du processus aléatoire! Une description aléatoire d'un processus aléatoire ne serait toujours pas confondue ici, ou même vouloir être confondue intentionnellement!

Qu'est-ce qui fait de la statistique mathématique une science exacte? Ses méthodes nous permettent de conclure notre ignorance dans un cadre clairement limité et de donner une mesure calculable de la confiance que, dans ce cadre, nos connaissances sont cohérentes avec les faits. C'est le langage dans lequel on peut raisonner sur des variables aléatoires inconnues pour que le raisonnement ait du sens. Une telle approche est très utile en philosophie, en psychologie ou en sociologie, où il est très facile de s'engager dans de longs raisonnements et discussions sans aucun espoir d'acquérir des connaissances positives et, surtout, des preuves. Beaucoup de littérature est consacrée au traitement compétent des données statistiques, car c'est un outil absolument nécessaire pour les médecins, les sociologues, les économistes, les physiciens, les psychologues ... en un mot, pour tous les scientifiques qui recherchent le soi-disant "monde réel", qui ne diffère de l'idéal mathématique que par le degré de notre ignorance à son sujet.

Examinons maintenant l'épigraphe de ce chapitre et réalisons que les statistiques, qui sont si dénigrement appelées le troisième degré de mensonges, sont les seules choses que possèdent les sciences naturelles. N'est-ce pas la loi principale de la bassesse de l'univers! Toutes les lois de la nature que nous connaissons, du physique à l'économie, sont basées sur des modèles mathématiques et leurs propriétés, mais elles sont vérifiées par des méthodes statistiques lors des mesures et des observations. Dans la vie de tous les jours, notre esprit fait des généralisations et observe des schémas, isole et reconnaît les images qui se répètent, c'est probablement le mieux que le cerveau humain puisse faire. C'est exactement ce que l'intelligence artificielle enseigne de nos jours. Mais l'esprit conserve sa force et est enclin à tirer des conclusions des observations individuelles, ne se souciant pas beaucoup de l'exactitude ou de la validité de ces conclusions. À cette occasion, il y a une merveilleuse déclaration cohérente du livre de Stephen Brast, Isola: «Tout le monde tire des conclusions générales d'un exemple. C'est du moins ce que je fais . » Et tandis que nous parlons d'art, de la nature des animaux de compagnie ou de politique, vous ne pouvez pas vous en préoccuper. Cependant, lors de la construction d'un avion, de l'organisation d'un service de répartition aéroportuaire ou de l'essai d'un nouveau médicament, vous ne pouvez plus faire référence au fait que «il me semble», «l'intuition raconte» et «tout se passe dans la vie». Ici, vous devez limiter votre esprit au cadre de méthodes mathématiques rigoureuses.

Notre livre n'est pas un manuel, et nous n'étudierons pas les méthodes statistiques en détail et nous limiterons à une seule chose - la technique de vérification des hypothèses. Mais je voudrais montrer le cours du raisonnement et la forme des résultats caractéristiques de ce champ de connaissance. Et, peut-être, certains lecteurs, le futur étudiant, comprendront non seulement pourquoi ils le tourmentent avec des statistiques, avec tous ces diagrammes QQ, distributions t et F, mais une autre question importante se posera: comment est-il possible de savoir quoi - sûrement d'un accident? Et qu'apprenons-nous exactement à l'aide des statistiques?

Trois baleines de statistiques

Les principaux piliers des statistiques mathématiques sont la théorie des probabilités, la loi des grands nombres et le théorème central limite .

La loi des grands nombres, dans une interprétation libre, suggère qu'un grand nombre d'observations d'une variable aléatoire reflète presque certainement sa distribution , de sorte que les statistiques observées: moyenne, variance et autres caractéristiques tendent à des valeurs exactes correspondant à la variable aléatoire. En d'autres termes, l'histogramme des valeurs observées avec un nombre infini de données tend presque certainement à la distribution que nous pouvons considérer comme vraie. C'est cette loi qui relie l'interprétation fréquentielle «quotidienne» de la probabilité et la théorie, en tant que mesures dans un espace de probabilité.

Le théorème central limite, encore une fois, dans une interprétation libre, dit que l'une des formes les plus probables de la distribution d'une variable aléatoire est une distribution normale (gaussienne). La formulation exacte semble différente: la valeur moyenne d'un grand nombre de variables aléatoires réelles réparties de manière identique, quelle que soit leur distribution, est décrite par la distribution normale. Ce théorème est généralement prouvé à l'aide de méthodes d'analyse fonctionnelle, mais nous verrons plus tard qu'il peut être compris et même développé en introduisant le concept d'entropie comme mesure de la probabilité d'un état système: une distribution normale a la plus grande entropie avec le moins de contraintes. En ce sens, il est optimal pour décrire une variable aléatoire inconnue, ou une variable aléatoire, qui est une combinaison de nombreuses autres variables, dont la distribution est également inconnue.

Ces deux lois sous-tendent des estimations quantitatives de la fiabilité de nos connaissances basées sur des observations. Nous parlons ici de confirmation statistique ou de réfutation de l'hypothèse, qui peut être faite à partir de quelques fondements communs et d'un modèle mathématique. Cela peut sembler étrange, mais en soi, les statistiques ne produisent pas de nouvelles connaissances. Un ensemble de faits ne se transforme en connaissance qu'après avoir établi des liens entre des faits qui forment une certaine structure. Ce sont ces structures et ces relations qui nous permettent de faire des prédictions et de faire des hypothèses générales basées sur quelque chose qui va au-delà des statistiques. Ces hypothèses sont appelées hypothèses . Il est temps de rappeler l'une des lois de la merphologie, le postulat de la Persigue :

Le nombre d'hypothèses raisonnables expliquant un phénomène donné est infini.

La tâche de la statistique mathématique est de limiter ce nombre infini, ou plutôt de le réduire à un, et pas nécessairement vrai du tout. Pour passer à une hypothèse plus complexe (et souvent plus souhaitable), il est nécessaire, à l'aide de données d'observation, de réfuter l'hypothèse plus simple et plus générale, ou de la renforcer et d'abandonner le développement ultérieur de la théorie. L'hypothèse souvent testée de cette manière est appelée nulle , et il y a un sens profond à cela.

Qu'est-ce qui peut agir comme une hypothèse nulle? Dans un certain sens, n'importe quoi, n'importe quelle déclaration, mais à condition qu'elle puisse être traduite dans le langage de la mesure. Le plus souvent, l'hypothèse est la valeur attendue d'un paramètre, qui se transforme en variable aléatoire lors de la mesure, ou l'absence de connexion (corrélation) entre deux variables aléatoires. Parfois, on suppose le type de distribution, un processus aléatoire, un modèle mathématique est proposé. La formulation classique de la question est la suivante: les observations permettent-elles ou non de rejeter l'hypothèse nulle? Plus précisément, avec quelle certitude pouvons-nous dire que des observations ne peuvent être obtenues sur la base de l'hypothèse nulle? De plus, si nous n'avons pas pu prouver, sur la base de données statistiques, que l'hypothèse nulle est fausse, alors elle est acceptée comme vraie.

Et ici, vous pourriez penser que les chercheurs sont obligés de faire l'une des erreurs logiques classiques, qui porte le nom latin sonore ad ignorantiam. Il s'agit d'un argument de la vérité d'une déclaration, basée sur le manque de preuves de sa fausseté. Un exemple classique est les paroles prononcées par le sénateur Joseph McCarthy lorsqu'il lui a été demandé de présenter des faits à l'appui de son accusation selon laquelle une certaine personne est un communiste: «J'ai peu d'informations à ce sujet, à l'exception de la déclaration générale des autorités compétentes selon laquelle il n'y a rien dans son dossier d'exclure ses liens avec les communistes . " Ou encore plus lumineux: "Bigfoot existe, car personne n'a prouvé le contraire . " L'identification de la différence entre une hypothèse scientifique et des astuces similaires fait l'objet de tout un champ de philosophie: la méthodologie de la connaissance scientifique . Un de ses résultats frappants est le critère de falsifiabilité , mis en avant par le remarquable philosophe Karl Popper dans la première moitié du XXe siècle. Ce critère vise à séparer les connaissances scientifiques des connaissances non scientifiques et, à première vue, il semble paradoxal:

Une théorie ou une hypothèse ne peut être considérée comme scientifique que s'il existe, même hypothétiquement, un moyen de la réfuter.

Quelle n'est pas la loi de la méchanceté! Il s'avère que toute théorie scientifique est automatiquement potentiellement incorrecte, et une théorie qui est vraie "par définition" ne peut pas être considérée comme scientifique. De plus, les sciences telles que les mathématiques et la logique ne satisfont pas à ce critère. Cependant, ils ne se réfèrent pas aux sciences naturelles , mais aux sciences formelles , qui ne nécessitent pas de test de falsifiabilité. Et si nous ajoutons un résultat supplémentaire de la même époque: le principe d’incomplétude de Gödel, qui stipule que dans tout système formel, il est possible de formuler une déclaration qui ne peut être ni prouvée ni réfutée, il peut devenir difficile de comprendre pourquoi, en général, s’engager dans toute cette science. Cependant, il est important de comprendre que le principe de falsifiabilité de Popper ne dit rien sur la vérité d’une théorie, mais seulement si elle est scientifique ou non. Cela peut aider à déterminer si une théorie donne un langage dans lequel il est logique de parler du monde ou non.

Mais encore, pourquoi, si nous ne pouvons pas rejeter l'hypothèse sur la base de données statistiques, avons-nous le droit de l'accepter comme vraie? Le fait est que l'hypothèse statistique n'est pas tirée du désir ou des préférences du chercheur, elle doit découler de toute loi formelle générale. Par exemple, à partir du théorème de limite centrale, ou du principe d'entropie maximale. Ces lois reflètent correctement le degré de notre ignorance , sans ajouter, inutilement, des hypothèses ou hypothèses inutiles. Dans un sens, il s'agit d'une utilisation directe du célèbre principe philosophique connu sous le nom de rasoir d'Occam :

Ce qui peut être fait sur la base de moins d'hypothèses ne devrait pas l'être sur la base de plus.

Ainsi, lorsque nous acceptons l'hypothèse nulle, basée sur l'absence de sa réfutation, nous montrons formellement et honnêtement qu'à la suite de l'expérience le degré de notre ignorance est resté au même niveau . Dans l'exemple du Bigfoot, explicitement ou implicitement, le contraire est supposé: le manque de preuves que cette mystérieuse créature ne semble pas être quelque chose qui peut augmenter le degré de nos connaissances à son sujet.

En général, du point de vue du principe de falsifiabilité, toute déclaration sur l'existence de quelque chose n'est pas scientifique, car le manque de preuves ne prouve rien. Dans le même temps, l'affirmation de l'absence de quoi que ce soit peut être facilement réfutée en fournissant une copie, une preuve indirecte ou en prouvant l'existence d'une construction. Et en ce sens, un test d'hypothèse statistique analyse les allégations d' absence de l' effet recherché et peut, en un sens, fournir une réfutation précise de cette affirmation. C'est exactement ce que le terme «hypothèse nulle» est pleinement justifié: il contient les connaissances minimales nécessaires sur le système.

Comment confondre les statistiques et comment démêler

Il est très important de souligner que si les statistiques indiquent que l'hypothèse nulle peut être rejetée, cela ne signifie pas que nous avons ainsi prouvé la vérité de toute hypothèse alternative.Les statistiques ne doivent pas être confondues avec la logique, c'est là que réside une masse d'erreurs subtiles, en particulier lorsque des probabilités conditionnelles pour des événements dépendants entrent en jeu. Par exemple: il est très peu probable qu'une personne puisse être le pape ($$~ 1 / 7 milliards) suivi de ce quepape JeanPaul II n'était pas un homme? La déclaration semble absurde, mais, malheureusement, une telle conclusion «évidente» est tout aussi fausse: le test a montré qu'un test mobile pour la teneur en alcool dans le sang ne donne plus$\sim 1/7$$$1 % des résultats faux positifs et faux négatifs$1\%$$$Dans 98 % des cas, il identifiera correctement un conducteur ivre. Testons$98\%$$$1000 conducteurs et laissez$1000$$$100 d'entre eux seront vraiment ivres. En conséquence, nous obtenons$100$$$900 × 1 % = 9 faux positifs et$900\times1\%=9$$$100 × 1 % = 1 résultat faussement négatif: c'est-à-dire que pour un ivrogne qui s'est glissé, il y aurait neuf conducteurs au hasard innocemment accusés. Quelle n'est pas la loi de la méchanceté! La parité ne sera observée que si la proportion de conducteurs ivres est égale à$100\times1\%=1$$$$1/2$ , . , , !

. , : . , , . : .
La probabilité d'intersection des événements A et B est définie comme le produit de la probabilité de l'événement B et de la probabilité de l'événement $$A , si l'on sait qu'un événement s'est produit$A$$$$B$ :

$$

$$P(A \cap B) = P(B)P(A|B).$$

Vous pouvez désormais déterminer l'indépendance des événements de trois manières équivalentes: Evénements $$$A$ et $$B indépendant si$B$$$P ( A | B ) = P ( A ) , ou$P(A|B) = P(A)$$$P ( B | A ) = P ( B ) , ou$P(B|A) = P(B)$$$$P(A\cap B) = P(A)P(B)$ .
Ceci complète la définition formelle de la probabilité commencée dans le premier chapitre.

L'intersection est une opération commutative, c'est-à-dire$$$P(A\cap B) = P(B\cap A)$ . Cela implique immédiatement le théorème bayésien:

$$

$$P(A|B)P(B) = P(B|A)P(A),$$

qui peut être utilisé pour calculer les probabilités conditionnelles.

Dans notre exemple avec chauffeurs et test d'alcoolémie, nous avons des événements:$$A - le conducteur est ivre,$A$$$Le test B a donné un résultat positif. Probabilités:$B$$$P ( A ) = 0,1 - la probabilité que le conducteur arrêté soit ivre;$P(A) = 0.1$$$P ( B | A ) = 99 % - la probabilité que le test donne un résultat positif si l'on sait que le conducteur est ivre (exclu$P(B|A) = 99\%$$$1 % de faux négatifs)$1\%$$$P ( A | B ) = 99 % - la probabilité que le test ait bu, si le test a donné un résultat positif (exclu$P(A|B) = 99\%$$$1 faux résultats positifs). Nous calculons$1%$$$$P (B)$ - la probabilité d'obtenir un résultat de test positif sur la route:

$$

$$P (B) = \ frac {P (A) P (A | B)} {P (B | A)} = P (A) = 0,1$$

Maintenant, notre raisonnement est devenu officiel et, comme vous le savez, peut-être pour certaines personnes plus compréhensible. Le concept de probabilité conditionnelle vous permet de raisonner logiquement dans le langage de la théorie des probabilités. Il n'est pas surprenant que le théorème de Bayes ait trouvé une large application dans la théorie de la décision, dans les systèmes de reconnaissance de formes, dans les filtres anti-spam, les programmes qui testent les tests de plagiat et dans de nombreuses autres technologies de l'information.

Ces exemples sont soigneusement compris par les étudiants des tests médicaux ou des pratiques juridiques. Mais, je crains que ni les statistiques mathématiques ni la théorie des probabilités ne soient enseignées aux journalistes ou aux politiciens, mais ils font appel avec impatience aux données statistiques, les interprètent librement et apportent les "connaissances" acquises aux masses. Par conséquent, j'exhorte mon lecteur: j'ai moi-même compris les mathématiques, aidez-moi à les découvrir pour une autre! Je ne vois aucun autre antidote à l'ignorance.

Nous mesurons notre crédulité

Nous ne considérerons et n'appliquerons en pratique qu'une des nombreuses méthodes statistiques: tester des hypothèses statistiques. Pour ceux qui ont déjà lié leur vie aux sciences naturelles ou sociales, il n'y aura pas quelque chose d'étonnamment nouveau dans ces exemples.

Supposons que nous mesurions à plusieurs reprises une variable aléatoire ayant une valeur moyenne $$$\ mu$ et écart type $$$\ sigma$ . Selon le théorème de la limite centrale, la valeur moyenne observée sera distribuée normalement. De la loi des grands nombres, il s'ensuit que sa moyenne aura tendance à $$$\ mu$ , et des propriétés de la distribution normale, il s'ensuit qu'après $$$n$ mesure, la variance observée de la moyenne diminuera à mesure que $$$\ sigma / \ sqrt {n}$ . L'écart type peut être considéré comme l'erreur absolue de la mesure moyenne, l'erreur relative dans ce cas sera égale à $$$\ delta = \ sigma / (\ sqrt {n} \ mu)$ . Ce sont des conclusions très générales, indépendantes de $$$n$ à partir de la forme de distribution spécifique de la variable aléatoire étudiée. Il en découle deux règles utiles (et non des lois):

1. Nombre minimum de tests $$$n$ doit être dicté par l'erreur relative souhaitée $$$\ delta$ . De plus, si

$$

$$n \ geq \ left (\ frac {2 \ sigma} {\ mu \ delta} \ right) ^ 2,$$

alors la probabilité que la moyenne observée reste dans l'erreur spécifiée sera au moins $$ . À $$$\ mu$ proche de zéro, l'erreur relative vaut mieux remplacer l'absolu.

2. Soit l'hypothèse nulle l'hypothèse que la moyenne observée est $$$\ mu$ . Ensuite, si la moyenne observée ne dépasse pas $$$\ mu \ pm 2 \ sigma / \ sqrt {n}$ , alors la probabilité que l'hypothèse nulle soit vraie sera au moins $$ .


En cas de remplacement dans ces règles $$$2 \ sigma$ sur $$$3 \ sigma$ , le degré de confiance augmentera $$ c'est une règle très forte $$$3 \ sigma$ , qui en sciences physiques sépare les hypothèses du fait établi expérimentalement.

Il nous sera utile d'envisager l'application de ces règles à la distribution de Bernoulli décrivant une variable aléatoire qui prend exactement deux valeurs, appelées conditionnellement «succès» et «échec», avec une probabilité de réussite donnée $$$p$ . Dans ce cas $$$\ mu = p$ et $$$\ sigma = \ sqrt {p (1-p)}$ , donc pour le nombre requis d'expériences et l'intervalle de confiance, nous obtenons

$$

$$n \ geq \ frac {4} {\ delta ^ 2} \ frac {1-p} {p} \ quad et \ quad np \ pm 2 \ sqrt {np (1-p)}.$$

La règle $$$2 \ sigma$ La distribution de Bernoulli peut être utilisée pour déterminer l'intervalle de confiance lors du traçage des histogrammes. Essentiellement, chaque barre de l'histogramme représente une variable aléatoire avec deux valeurs: «hit» - «raté», où la probabilité de toucher correspond à une fonction de probabilité simulée. À titre de démonstration, nous allons générer de nombreux échantillons pour trois distributions: uniforme, géométrique et normale, après quoi nous comparons les estimations de la diffusion des données observées avec la diffusion observée. Et là encore, nous voyons les échos du théorème de la limite centrale, qui se manifestent par le fait que la distribution des données autour des valeurs moyennes dans les histogrammes est proche de la normale. Cependant, près de zéro, la dispersion devient asymétrique et se rapproche d'une autre distribution très probable - exponentielle. Cet exemple montre bien ce que je voulais dire en disant que dans les statistiques, nous avons affaire à des valeurs aléatoires de paramètres d'une variable aléatoire.


Exemple montrant le rapport de l'estimation de dispersion faite par la règle $$$2 \ sigma$ et l'écart observé pour trois variables aléatoires.

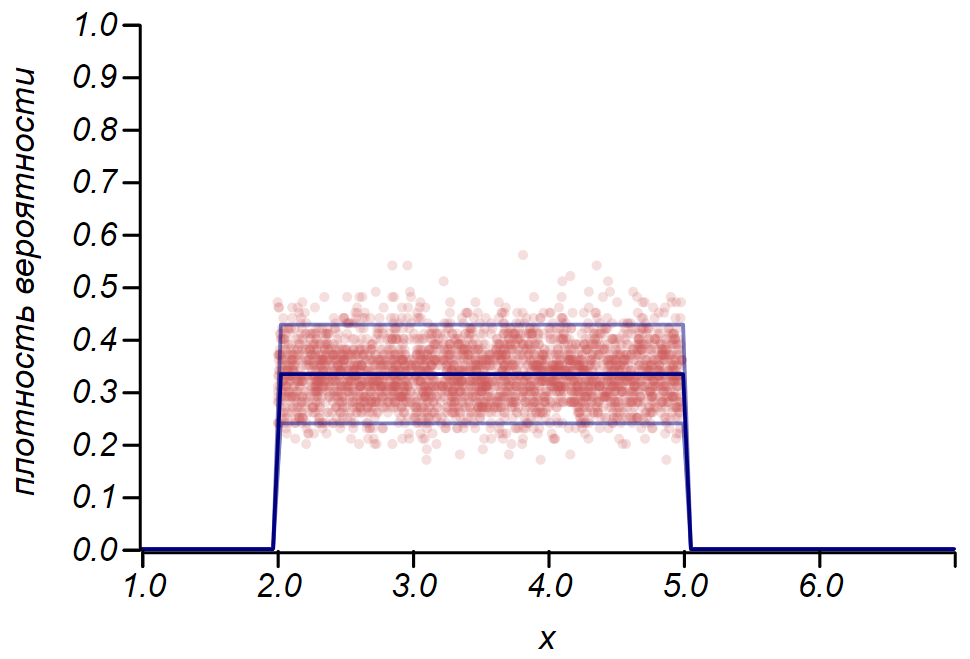
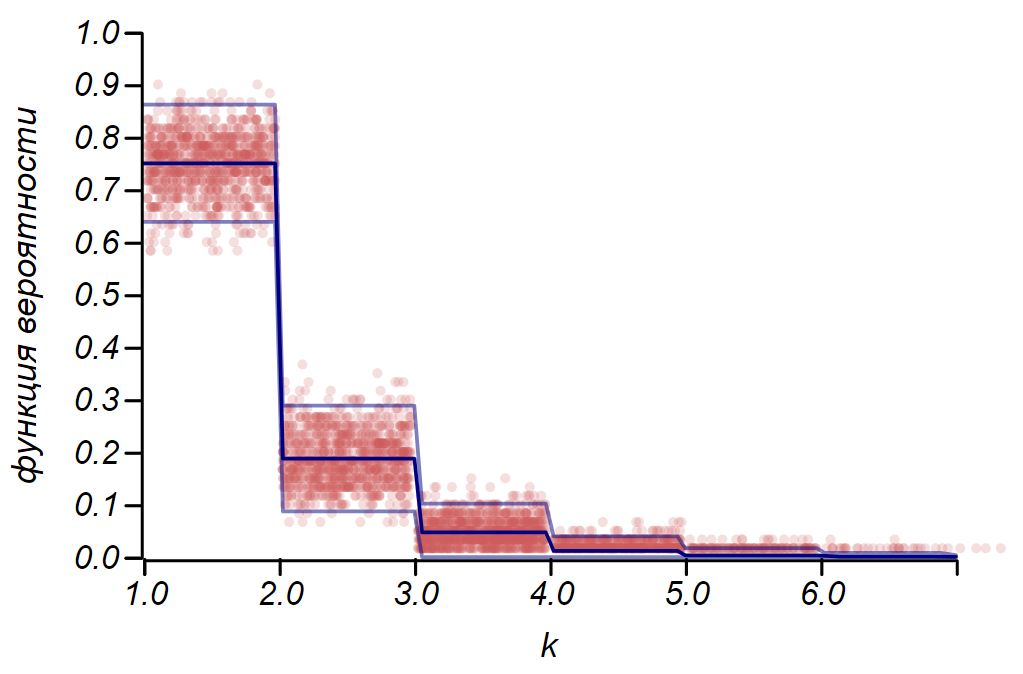
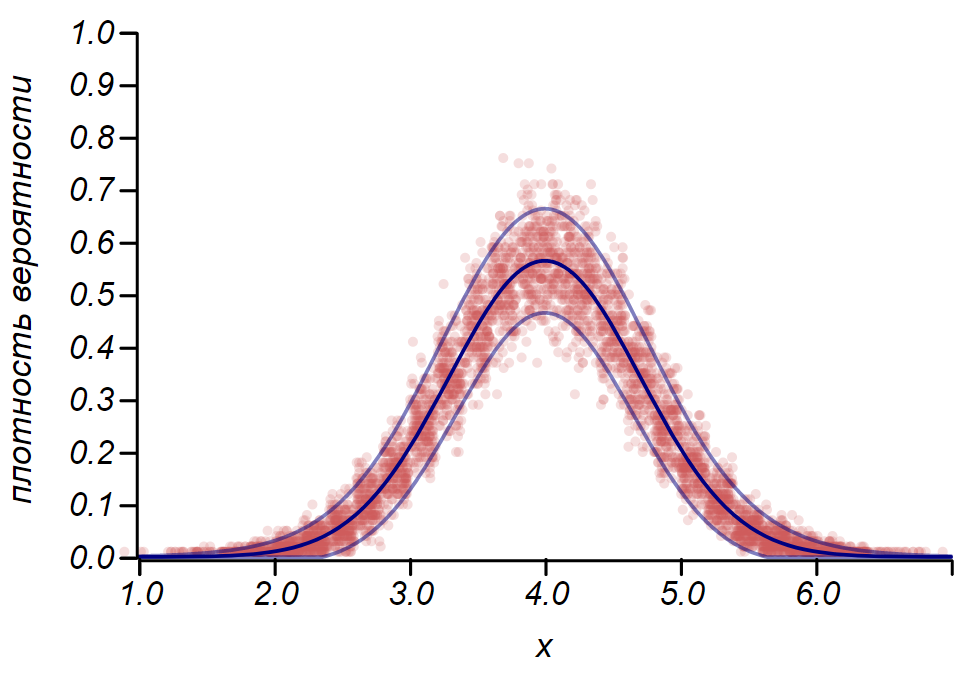
Il est important de comprendre que les règles $$$2 \ sigma$ et même $$$3 \ sigma$ ne nous sauve pas des erreurs. Ils ne garantissent la véracité d'aucune déclaration, ne sont pas des preuves. Les statistiques limitent le degré de méfiance d'une hypothèse, et rien de plus.

Le mathématicien et auteur d'un excellent cours de théorie des probabilités, Gian Carlo Rota, a donné un exemple lors de ses conférences au MIT. Imaginez une revue scientifique dont les rédacteurs ont pris une décision volontariste: accepter pour publication exclusivement des articles avec des résultats positifs qui satisfont à la règle $$$2 \ sigma$ ou plus strict. Dans le même temps, la colonne éditoriale indique que les lecteurs peuvent être sûrs qu'avec la probabilité $$ le lecteur ne trouvera pas le mauvais résultat sur les pages de ce magazine! Hélas, cette affirmation peut facilement être réfutée par le même raisonnement qui nous a conduit à une injustice flagrante lors des tests de dépistage d'alcool chez les conducteurs. Soit $$$1000$ chercheurs expérimentés $$$1000$ hypothèses, dont seule une partie est vraie, disons, $$ . Sur la base de la signification du test d'hypothèse, nous pouvons nous attendre à ce que $$ des hypothèses incorrectes ne seront pas rejetées par erreur et seront enregistrées avec $$ de vrais résultats. Total de $$$130$ Un bon tiers aura tort!

Cet exemple illustre parfaitement notre loi nationale de la méchanceté, qui n'a pas encore été incluse dans l'anthologie de la mérphologie, la loi de Tchernomyrdine :

Nous voulions le meilleur, mais il s'est avéré, comme toujours.

Il est facile d'obtenir une estimation générale du pourcentage de résultats incorrects qui seront inclus dans les numéros de la revue, en supposant que la part des vraies hypothèses est $$$0 <\ alpha <1$ et la probabilité d'accepter une hypothèse erronée est égale à $$$p$ :

$$

$$x = \ frac {(1- \ alpha) p} {\ alpha (1-p) + (1- \ alpha) p}.$$

Les zones limitant la part des résultats délibérément incorrects pouvant être publiés dans la revue sont illustrées dans la figure.

Estimation du pourcentage de publications contenant des résultats manifestement incorrects lors de l'adoption de différents critères de test d'hypothèses. On peut voir que l'acceptation d'hypothèses par la règle $$$2 \ sigma$ peut être risqué alors que le critère $$$4 \ sigma$ peut déjà être considéré comme très fort.

Bien sûr, nous ne le savons pas. $$$\ alpha$ , et nous ne le saurons jamais, mais c'est certainement moins que l'unité, ce qui signifie que, en tout cas, la déclaration de la colonne éditoriale ne peut pas être prise au sérieux. Vous pouvez vous limiter à des critères rigides $$$4 \ sigma$ mais cela nécessite un très grand nombre de tests. Par conséquent, il est nécessaire d'augmenter la part des vraies hypothèses dans l'ensemble des hypothèses possibles. Les approches standard de la méthode scientifique de la cognition visent à cela - la cohérence logique des hypothèses, leur cohérence avec les faits et les théories qui ont prouvé leur applicabilité, le recours aux modèles mathématiques et la pensée critique.

Et encore une fois sur la météo

Au début du chapitre, nous avons parlé du fait que les week-ends et le mauvais temps coïncident plus souvent que nous le souhaiterions. Essayons de terminer cette étude. Chaque jour de pluie peut être considéré comme l'observation d'une variable aléatoire - le jour de la semaine obéissant à la distribution de Bernoulli avec probabilité $$$1/7$ . Supposons, comme hypothèse nulle, l'hypothèse que tous les jours de la semaine sont les mêmes en termes de temps et de pluie peut pleuvoir dans l'un d'eux tout aussi probable. Nous avons deux jours de congé, nous obtenons donc la probabilité attendue d'une coïncidence d'une mauvaise journée et d'un jour de congé égal $$ , cette valeur sera le paramètre de distribution de Bernoulli. À quelle fréquence pleut-il? À différents moments de l'année, de différentes manières, bien sûr, mais à Petropavlovsk-Kamchatsky, en moyenne, il y a quatre-vingt-dix jours de pluie ou de neige en une année. Ainsi, le flux de jours avec des précipitations a une intensité d'environ $$ . Calculons le nombre de week-ends pluvieux que nous devons enregistrer afin d'être sûr qu'il existe un modèle. Les résultats sont présentés dans le tableau.

Période d'observation	été	année	$$ années
Nombre prévu d'observations	$$$23$	$$	$$
Nombre attendu de résultats positifs	$$	$$	$$$130$
Écart significatif	$$$4$	$$	$$
Proportion importante de mauvais nombre total de jours de congé	$$$42 \%$	$$$33 \%$	$$

De quoi parlent ces chiffres? S'il vous semble que pendant un an d'affilée il n'y a pas eu «d'été», que le rock maléfique poursuit votre week-end en leur envoyant de la pluie, cela peut être vérifié et confirmé. Cependant, pendant l'été, la roche maléfique ne peut être attrapée que si plus des deux cinquièmes de tous les week-ends se révèlent pluvieux. L'hypothèse nulle suggère que seul un quart du week-end devrait coïncider avec des intempéries. En cinq ans d'observation, on peut déjà espérer constater des écarts subtils qui vont au-delà $$$5 \%$ et, si nécessaire, procédez à leur explication.

J'ai profité du journal météo de l'école, qui a été réalisé de 2014 à 2018, et j'ai découvert ce qui s'est passé au cours de ces cinq années $$ jours pluvieux d'entre eux $$$141$ est tombé le week-end. C'est, en effet, plus que le nombre attendu par $$$11$ jours, mais des écarts importants commencent avec $$ jours, donc cela, comme nous l'avons dit dans l'enfance: "ne compte pas." Voici une série de données et un histogramme montrant la distribution des intempéries par jour de la semaine. Les lignes horizontales de l'histogramme indiquent l'intervalle dans lequel une déviation aléatoire de la distribution uniforme peut être observée pour la même quantité de données.


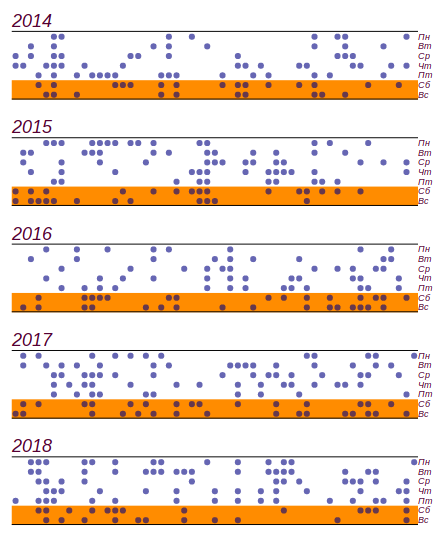
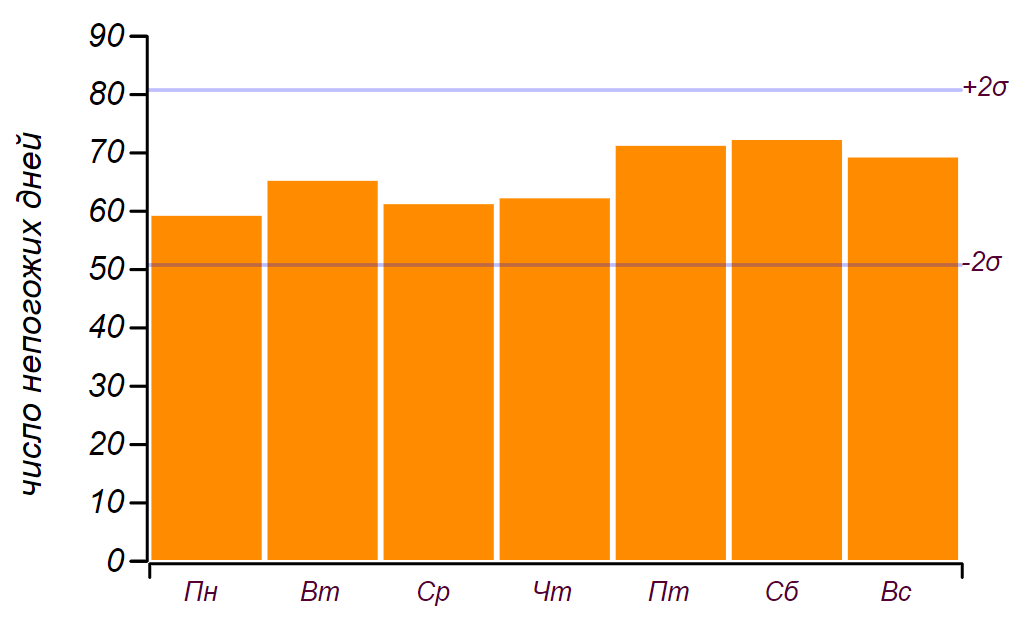La série initiale de données et la répartition des mauvais jours par jours de la semaine ont été obtenues sur cinq ans d'observation.

On peut voir que depuis vendredi, en effet, il y a eu une augmentation du nombre de jours de mauvais temps. Mais les prérequis ne suffisent pas à trouver une raison à cette croissance: le même résultat peut être obtenu simplement en triant par nombres aléatoires. Conclusion: pendant cinq ans d'observation du temps, j'ai accumulé près de deux mille enregistrements, mais je n'ai rien appris de nouveau sur la répartition du temps par jour de la semaine.

Lorsque vous regardez les entrées du journal, il est clairement évident que le temps ne vient pas seul, mais en périodes de deux à trois jours ou même des cyclones hebdomadaires. Est-ce que cela affecte en quelque sorte le résultat? Vous pouvez essayer de prendre en compte cette observation et supposer qu'il pleut en moyenne pendant deux jours (en fait, $$ jours), la probabilité de bloquer le week-end augmente à $$ . Avec une telle probabilité, le nombre attendu de matchs sur cinq ans devrait être $$ , c'est-à-dire de $$ avant $$$216$ fois. Valeur observée $$$141$ ne tombe pas dans cette fourchette et, par conséquent, l'hypothèse de l'effet de deux jours de mauvais temps peut être rejetée en toute sécurité. Avons-nous appris quelque chose de nouveau? Oui, nous avons appris: il semblerait qu'une caractéristique évidente du processus n'entraîne aucun effet. Cela vaut la peine d'être considéré, et nous le ferons un peu plus tard. Mais la principale conclusion est qu'il n'y a aucune raison d'envisager des effets plus subtils, car les observations et, surtout, leur nombre, parlent systématiquement en faveur de l'explication la plus simple.

Mais notre mécontentement n'est pas des statistiques quinquennales ni même annuelles, la mémoire humaine n'est pas si longue. C'est dommage quand il pleut le week-end trois ou quatre fois de suite! À quelle fréquence cela peut-il être observé? Surtout si vous vous souvenez que le mauvais temps ne vient pas seul. La tâche peut être formulée comme suit: «Quelle est la probabilité que $$$n$ week-end de suite sera pluvieux? " Il est raisonnable de supposer que le mauvais temps forme un courant de Poisson avec une intensité $$$1/4$ . Cela signifie qu'en moyenne, un quart des jours d'une période sera mauvais. En n'observant que le week-end, il ne faut pas changer l'intensité du débit, et de tous les week-ends le mauvais temps devrait être, en moyenne, également d'un quart. Nous proposons donc l'hypothèse nulle: la tempête est Poisson, avec un paramètre connu, ce qui signifie que les intervalles entre les événements de Poisson sont décrits par une distribution exponentielle. Nous nous intéressons aux intervalles discrets: $$$0, \ 1, \ 2, \ 3$ jours, etc. donc nous pouvons utiliser l'analogue discret de la distribution exponentielle - la distribution géométrique avec le paramètre $$$1/4$ . La figure montre ce que nous avons fait et on peut voir que l'hypothèse selon laquelle nous observons le processus de Poisson n'est pas raisonnable à rejeter.


La distribution observée de la longueur des chaînes de week-ends ratés et théorique. La ligne mince montre les écarts admissibles pour le nombre d'observations que nous avons.

Vous pouvez vous poser cette question: de combien d’années avez-vous besoin pour faire des observations afin que la différence $$$11$ jours pourraient être confirmés ou rejetés en toute confiance comme un écart aléatoire? C'est facile à calculer: probabilité observée $$ différent de celui attendu $$ sur $$ . Pour enregistrer les différences en centièmes, une erreur absolue ne dépassant pas $$ cela fait $$ à partir de la taille mesurée. De là, nous obtenons la taille d'échantillon requise $$$n \ geq (4 \ cdot 5/7) / (0,0175 ^ 2 \ cdot 2/7) \ environ 32000$ jours de pluie. Il faudra environ $$ années d'observations météorologiques continues, car il ne pleut ou ne neige que tous les quatre jours. Hélas, c'est plus que l'époque où le Kamtchatka fait partie de la Russie, donc je n'ai aucune chance de découvrir comment les choses sont "vraiment". Surtout si vous prenez en compte le fait que pendant ce temps le climat a réussi à changer radicalement - à partir de la petite période glaciaire, la nature est sortie à l'optimum suivant.

Alors, comment les chercheurs australiens ont-ils réussi à enregistrer l'écart de température en fractions de degré et pourquoi il est logique d'envisager cette étude? Le fait est qu'ils ont utilisé des données de température horaires qui n'ont pas été «éclaircies» par un quelconque processus aléatoire. Au-delà $$ années d'observations météorologiques ont réussi à accumuler plus d'un quart de million de relevés, ce qui permet de réduire l'écart type de la moyenne $$ fois par rapport à l'écart de température quotidien standard. Cela suffit pour parler de précision en dixièmes de degré. De plus, les auteurs ont utilisé une autre belle méthode qui confirme la présence d'un cycle temporel: le mélange aléatoire des séries chronologiques. Un tel mélange préserve les propriétés statistiques, telles que l'intensité du débit, cependant, il «efface» les modèles temporels, ce qui rend le processus vraiment Poisson. La comparaison de nombreuses séries synthétiques et expérimentales permet de vérifier que les écarts observés du processus par rapport à Poisson sont significatifs. De la même manière, le sismologue A. A. Gusev a montré que les tremblements de terre dans n'importe quelle région forment une sorte d'écoulement auto-similaire avec les propriétés de regroupement. Cela signifie que les tremblements de terre ont tendance à se regrouper dans le temps, formant des joints d'écoulement très désagréables. Plus tard, il s'est avéré que la séquence de grandes éruptions volcaniques a la même propriété.

Une autre source de hasard

Bien sûr, le temps, comme les tremblements de terre, ne peut pas être décrit par le processus de Poisson - ce sont des processus dynamiques dans lesquels l'état actuel est fonction des précédents. Pourquoi nos observations météorologiques hebdomadaires favorisent-elles un modèle stochastique simple? Le fait est que nous affichons le processus régulier de formation des précipitations pendant un ensemble de sept jours, ou, parlant le langage des mathématiques, sur un système de déductions modulo sept . Ce processus de projection est capable de générer du chaos à partir de séries de données bien ordonnées. À partir d'ici, par exemple, il y a un caractère aléatoire visible dans la séquence de chiffres de la notation décimale de la plupart des nombres réels.

Nous avons déjà parlé des nombres rationnels, ceux exprimés en fractions entières. Ils ont une structure interne, qui est déterminée par deux nombres: le numérateur et le dénominateur. Mais lors de l'écriture sous forme décimale, vous pouvez observer des sauts de régularité dans la représentation des nombres tels que $$$1/2 = 0,5 \ overline {0}$ , ou $$$1/3 = 0. \ Overline {3}$ à la répétition périodique de séquences déjà assez aléatoires en nombres tels que $$ . Les nombres irrationnels n'ont pas de notation décimale finie ou périodique, et dans ce cas, le chaos règne le plus souvent dans une séquence de nombres. Mais cela ne signifie pas qu'il n'y a pas d'ordre dans ces chiffres! Par exemple, le premier nombre irrationnel rencontré par les mathématiciens $$$\ sqrt {2}$ en notation décimale génère un ensemble aléatoire de nombres. Cependant, d'autre part, ce nombre peut être représenté comme une fraction continue infinie:

$$

$$\ sqrt {2} = 1 + \ frac {1} {2+ \ frac {1} {2+ \ frac {1} {2+ ...}}}.$$

Il est facile de montrer que cette chaîne est en effet égale à la racine de deux en résolvant l'équation:

$$

$$x-1 = \ frac {1} {2+ (x-1)}.$$

Les fractions continues avec des coefficients répétitifs sont écrites brièvement, comme les fractions décimales périodiques, par exemple: $$$\ sqrt {2} = [1, \ bar {2}]$ , $$$\ sqrt {3} = [1, \ overline {1,2}]$ . Le fameux nombre d'or dans ce sens est le nombre irrationnel le plus simplement arrangé: $$$\ varphi = [1, \ bar {1}]$ . Tous les nombres rationnels sont représentés sous la forme de fractions continues finies, certaines irrationnelles - sous la forme d'infinies, mais périodiques, elles sont appelées algébriques , les mêmes qui n'ont pas de notation finie même sous cette forme - transcendantales . Le plus célèbre des transcendantaux est le nombre $$$\ pi$ , il crée le chaos en décimal et sous forme de fraction continue: $$$\ pi \ environ [3, 7,15,1,292,1,1,1,2,1,3,1,14,2,1, ...]$ . Et voici le nombre d'Euler $$$e$ transcendantale restante, sous la forme d'une fraction continue, affiche la structure interne cachée dans la notation décimale: $$$e \ environ [2,1,2,1,1,4,1,1,6,1,1,8,1,1,10, ...]$ .

Probablement, aucun mathématicien, à commencer par Pythagore, n'a soupçonné le monde de la ruse, découvrant ce qui est nécessaire, un nombre aussi fondamental $$ p i a une structure chaotique si difficile à comprendre. Bien sûr, il peut être représenté comme des sommes de séries numériques assez élégantes, mais ces séries ne parlent pas directement de la nature de ce nombre et elles ne sont pas universelles. Je crois que les mathématiciens du futur découvriront une nouvelle représentation des nombres, aussi universelle que les fractions continues, qui révèlera l'ordre strict caché par la nature dans les nombres.$\ pi$

$$

$$*\ *\ *$$

Les résultats de ce chapitre sont pour la plupart négatifs. Et en tant qu'auteur qui veut surprendre le lecteur avec des motifs cachés et des découvertes inattendues, je me demandais si cela devait être inclus dans le livre. Mais notre conversation sur le temps est entrée dans un sujet très important - la valeur et le sens de l'approche des sciences naturelles.

Une fille sage, Sonya Shatalova, regardant le monde à travers le prisme de l'autisme, à l'âge de dix ans, a donné une définition très concise et précise: «La science est un système de connaissances basé sur le doute». Le monde réel est instable et s'efforce de se cacher derrière la complexité, le caractère aléatoire visible et le manque de fiabilité des mesures. Le doute dans les sciences naturelles est inévitable. Les mathématiques semblent être un domaine de certitude, dans lequel, semble-t-il, on peut oublier le doute. Et il est très tentant de se cacher derrière les murs de ce royaume; considérer au lieu des modèles mondiaux méconnaissables qui peuvent être étudiés en profondeur; compter et calculer, le bénéfice de la formule est prêt à tout digérer. Mais néanmoins, les mathématiques sont une science et le doute est une profonde honnêteté intérieure qui ne donne pas de repos tant que la construction mathématique n'est pas débarrassée d'hypothèses supplémentaires et d'hypothèses inutiles. Dans le domaine des mathématiques, ils parlent un langage complexe mais harmonieux, adapté au raisonnement sur le monde réel. Il est très important de se familiariser un peu avec cette langue,afin d'empêcher les chiffres de se faire passer pour des statistiques, de ne pas laisser les faits prétendre être des connaissances, et l'ignorance et la manipulation contrastent avec la vraie science.