Bonjour à tous! Je m'appelle Grisha et je suis le fondateur de CGDevs. Continuons à parler de mathématiques ou de quelque chose. Peut-être la principale application des mathématiques dans le développement de jeux et l'infographie en général est VFX. Parlons donc d'un tel effet - la pluie, ou plutôt de sa partie principale, qui nécessite des mathématiques - des ondulations à la surface. Écrivez successivement un shader pour les ondulations sur la surface et analysez ses mathématiques. Si vous êtes intéressé - bienvenue au chat. Projet Github joint.
Parfois, il arrive un moment dans la vie où un programmeur doit saisir un tambourin et appeler à la pluie. En général, le sujet de la modélisation de la pluie elle-même est très profond. Il existe de nombreux travaux mathématiques sur différentes parties de ce processus, depuis la chute des gouttes et les effets qui y sont associés jusqu'à la distribution des gouttelettes en volume. Nous n'analyserons qu'un seul aspect - le shader, qui nous permettra de créer un effet similaire à l'onde d'une goutte tombée. Il est temps de prendre un tambourin!
Vague mathématiqueLorsque vous recherchez sur Internet, vous trouverez de nombreuses expressions mathématiques amusantes pour générer des ondulations. Souvent, ils consistent en une sorte de nombres "magiques" et de fonctions périodiques sans justification. Mais en général, les mathématiques de cet effet sont assez simples.
Nous n'avons besoin que d'une équation d'onde plane dans le cas unidimensionnel. Pourquoi nous analyserons un peu et à plat un peu plus tard.
L'équation des ondes planes dans notre cas peut s'écrire:
Aresult = A * cos (2 * PI * (x / waveLength - t * fréquence));Où:
Résultat - amplitude au point x, au temps t
A est l'amplitude maximale
longueur d'onde - longueur d'onde
fréquence - fréquence d'onde
PI - Numéro
PI = 3,14159 (flottant)
ShaderJouons avec les shaders. Pour le "haut" sera responsable de la coordonnée -Z. C'est plus pratique dans le cas 2D dans Unity. Si vous le souhaitez, le shader ne sera pas difficile à réécrire en Y.
La première chose dont nous avons besoin est l'équation d'un cercle. L'onde de notre shader sera symétrique par rapport au centre. L'équation du cercle dans le cas 2d est décrite comme suit:
r ^ 2 = x ^ 2 + y ^ 2nous avons besoin d'un rayon, donc l'équation prend la forme:
r = sqrt (x ^ 2 + y ^ 2)et cela nous donnera une symétrie par rapport au point (0, 0) dans le maillage, ce qui réduira tout au cas unidimensionnel d'une onde plane.
Écrivons maintenant un shader. Je n'analyserai pas chaque étape de l'écriture d'un shader, car ce n'est pas le but de l'article, mais la base est tirée du Shader de surface standard d'Unity, dont le modèle peut être obtenu via Create-> Shader-> StandardSurfaceShader.
De plus, les propriétés nécessaires à l'équation d'onde sont
ajoutées :
_Frequency ,
_WaveLength et
_WaveHeight . Propriété
_Timer (il serait possible d'utiliser le temps avec hcp, mais pendant le développement et l'animation suivante, il est plus pratique de le contrôler manuellement.
Nous écrivons la fonction getHeight pour obtenir la hauteur (maintenant c'est la coordonnée Z) en substituant l'équation du cercle dans l'équation d'onde
En écrivant un shader avec notre équation d'onde et l'équation de cercle, nous obtenons cet effet.
Code de shaderShader "CGDevs/Rain/RainRipple" { Properties { _WaveHeight("Wave Height", float) = 1 _WaveLength("Wave Length", float) = 1 _Frequency("Frequency", float) = 1 _Timer("Timer", Range(0,1)) = 0 _Color ("Color", Color) = (1,1,1,1) _MainTex ("Albedo (RGB)", 2D) = "white" {} _Glossiness ("Smoothness", Range(0,1)) = 0 _Metallic ("Metallic", Range(0,1)) = 0.0 } SubShader { Tags { "RenderType"= "Opaque" } LOD 200 CGPROGRAM #pragma surface surf Standard fullforwardshadows vertex:vert #pragma target 3.0 sampler2D _MainTex; struct Input { float2 uv_MainTex; }; half _Glossiness, _Metallic, _Frequency, _Timer, _WaveLength, _WaveHeight; fixed4 _Color; half getHeight(half x, half y) { const float PI = 3.14159; half rad = sqrt(x * x + y * y); half wavefunc = _WaveHeight * cos(2 * PI * (_Frequency * _Timer - rad / _WaveLength)); return wavefunc; } void vert (inout appdata_full v) { v.vertex.z -= getHeight(v.vertex.x, v.vertex.y); } void surf (Input IN, inout SurfaceOutputStandard o) { fixed4 c = tex2D (_MainTex, IN.uv_MainTex) * _Color; o.Albedo = c.rgb; o.Metallic = _Metallic; o.Smoothness = _Glossiness; o.Alpha = _Color.a; } ENDCG } FallBack "Diffuse" }
Il y a des vagues. Mais je veux que l'animation commence et se termine avec un avion. La fonction sinus nous y aidera. En multipliant l'amplitude par le péché (_Timer * PI), nous obtenons une apparence lisse et la disparition des ondes. Puisque _Timer prend des valeurs de 0 à 1, et que le sinus à zéro et dans PI est nul, c'est exactement ce dont vous avez besoin.
Bien que ce ne soit pas du tout comme une goutte qui tombe. Le problème est que l'énergie des vagues est perdue uniformément. Ajoutez la propriété _Radius, qui sera responsable du rayon de l'effet. Et nous multiplions l'amplitude de la pince (_Radius - rad, 0, 1) et obtenons déjà un effet plus similaire à la vérité.
Eh bien, la dernière étape. Le fait que l'amplitude à chaque point individuel atteigne son maximum à un temps égal à 0,5 n'est pas tout à fait vrai, il vaut mieux remplacer cette fonction.
Ensuite, je me suis senti un peu trop paresseux pour compter, et j'ai simplement multiplié le sinus par (1 - _Timer) et obtenu une telle courbe.
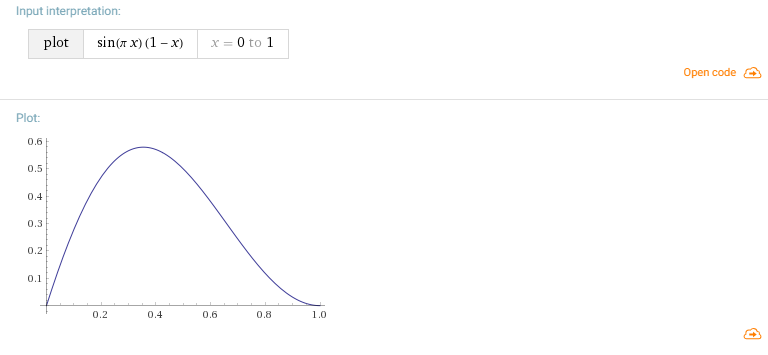
Mais en général, du point de vue des mathématiques, vous pouvez également sélectionner ici la courbe souhaitée en fonction de la logique à quel moment vous voulez un pic et une forme approximative, puis créer une interpolation à ces points.
Le résultat est un tel shader et effet.
Code de shader Shader "CGDevs/Rain/RainRipple" { Properties { _WaveHeight("Wave Height", float) = 1 _WaveLength("Wave Length", float) = 1 _Frequency("Frequency", float) = 1 _Radius("Radius", float) = 1 _Timer("Timer", Range(0,1)) = 0 _Color ("Color", Color) = (1,1,1,1) _MainTex ("Albedo (RGB)", 2D) = "white" {} _Glossiness ("Smoothness", Range(0,1)) = 0 _Metallic ("Metallic", Range(0,1)) = 0.0 } SubShader { Tags { "RenderType"= "Opaque" } LOD 200 CGPROGRAM #pragma surface surf Standard fullforwardshadows vertex:vert #pragma target 3.0 sampler2D _MainTex; struct Input { float2 uv_MainTex; }; half _Glossiness, _Metallic, _Frequency, _Timer, _WaveLength, _WaveHeight, _Radius; fixed4 _Color; half getHeight(half x, half y) { const float PI = 3.14159; half rad = sqrt(x * x + y * y); half wavefunc = _WaveHeight * sin(_Timer * PI) * (1 - _Timer) * clamp(_Radius - rad, 0, 1) * cos(2 * PI * (_Frequency * _Timer - rad / _WaveLength)); return wavefunc; } void vert (inout appdata_full v) { v.vertex.z -= getHeight(v.vertex.x, v.vertex.y); } void surf (Input IN, inout SurfaceOutputStandard o) { fixed4 c = tex2D (_MainTex, IN.uv_MainTex) * _Color; o.Albedo = c.rgb; o.Metallic = _Metallic; o.Smoothness = _Glossiness; o.Alpha = _Color.a; } ENDCG } FallBack "Diffuse" }
Revenons un peu au sujet de l'
article précédent . Les vagues sont implémentées par le vertex shader, donc le maillage du maillage joue un rôle assez important. La nature du mouvement étant connue, la tâche est simplifiée, mais en général, le visuel final dépend de la forme de la grille. La différence devient insignifiante avec une forte polygonalité, mais pour les performances, moins il y a de polygones, mieux c'est. Vous trouverez ci-dessous des images illustrant la différence entre les grilles et les visuels.
Correctement: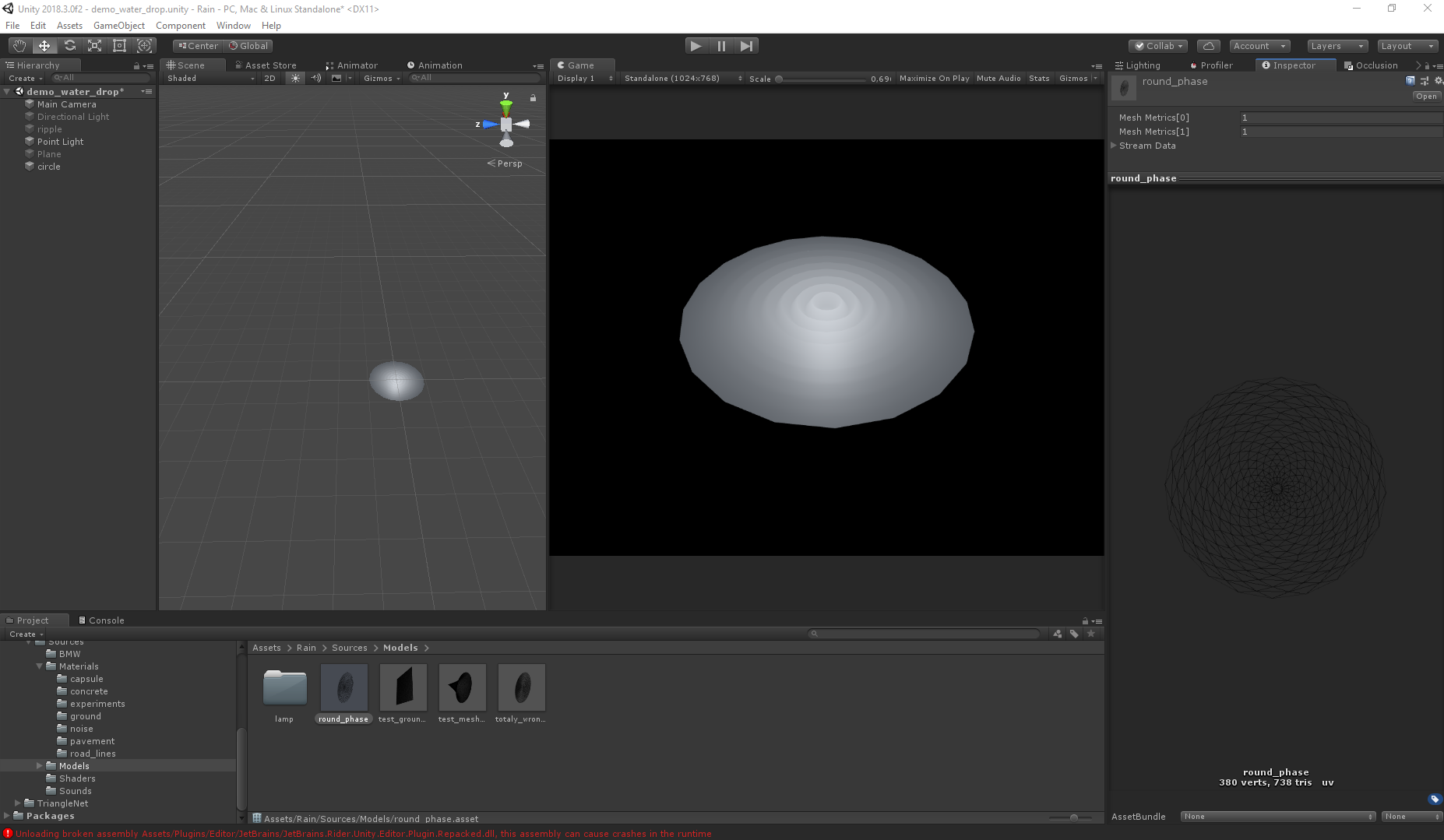
Mauvais: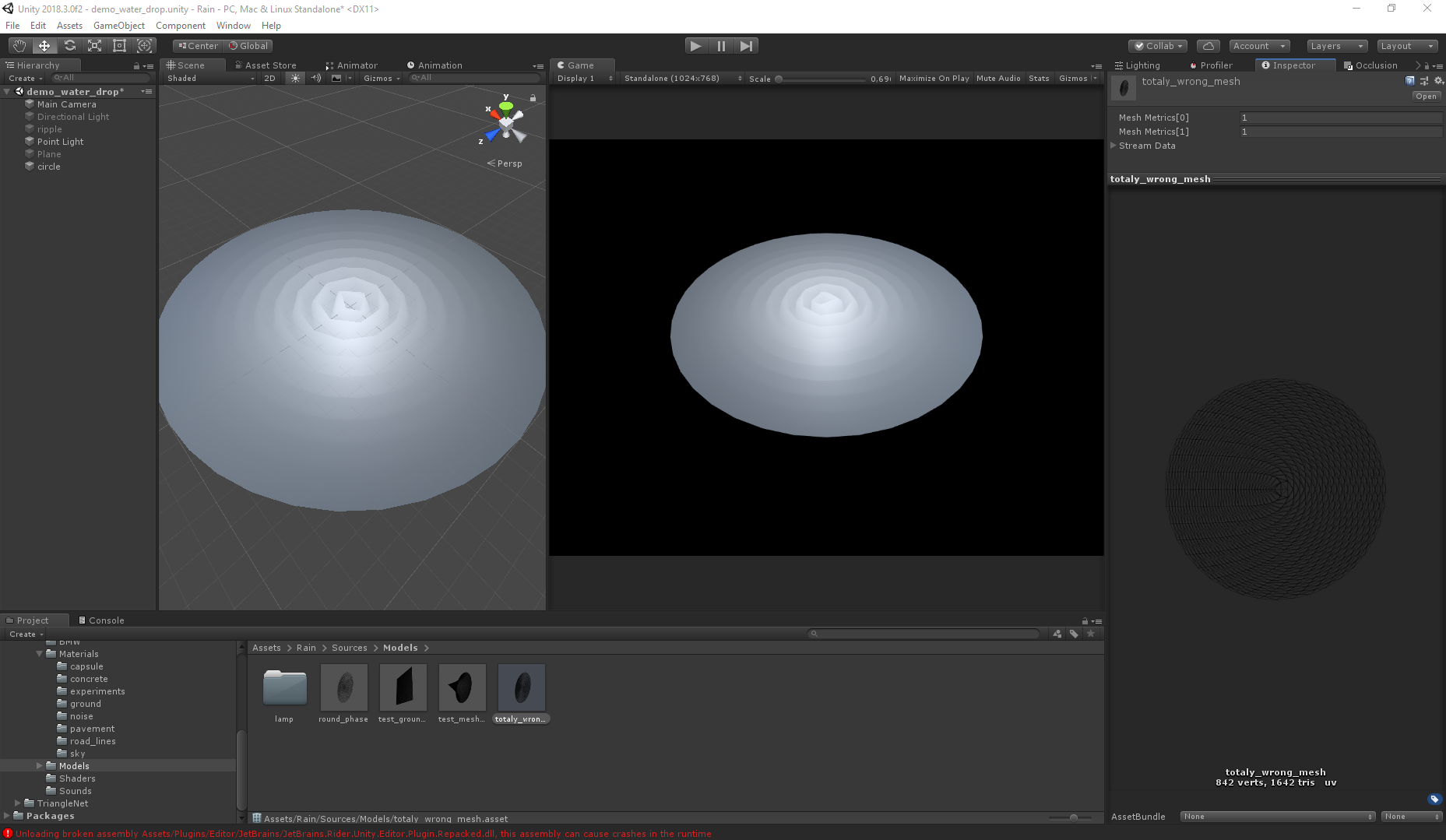
Même avec deux fois plus de polygones, le deuxième maillage donne le mauvais visuel (les deux maillages sont générés en utilisant Triangle.Net, en utilisant simplement des algorithmes différents).
Visuel finalDans une version différente du shader, une partie spéciale a été ajoutée pour créer des vagues non pas strictement au centre, mais en plusieurs points. Comment cela est mis en œuvre et comment vous pouvez transmettre ces paramètres, je peux dire dans les articles suivants, si le sujet est intéressant.
Voici le shader lui-même:
Sommet ondulé avec pôle Shader "CGDevs/Rain/Ripple Vertex with Pole" { Properties { _MainTex ("Albedo (RGB)", 2D) = "white" {} _Normal ("Bump Map", 2D) = "white" {} _Roughness ("Metallic", 2D) = "white" {} _Occlusion ("Occlusion", 2D) = "white" {} _PoleTexture("PoleTexture", 2D) = "white" {} _Color ("Color", Color) = (1,1,1,1) _Glossiness ("Smoothness", Range(0,1)) = 0 _WaveMaxHeight("Wave Max Height", float) = 1 _WaveMaxLength("Wave Length", float) = 1 _Frequency("Frequency", float) = 1 _Timer("Timer", Range(0,1)) = 0 } SubShader { Tags { "IgnoreProjector" = "True" "RenderType" = "Opaque"} LOD 200 CGPROGRAM #pragma surface surf Standard fullforwardshadows vertex:vert #pragma target 3.0 sampler2D _PoleTexture, _MainTex, _Normal, _Roughness, _Occlusion; half _Glossiness, _WaveMaxHeight, _Frequency, _Timer, _WaveMaxLength, _RefractionK; fixed4 _Color; struct Input { float2 uv_MainTex; }; half getHeight(half x, half y, half offetX, half offetY, half radius, half phase) { const float PI = 3.14159; half timer = _Timer + phase; half rad = sqrt((x - offetX) * (x - offetX) + (y - offetY) * (y - offetY)); half A = _WaveMaxHeight * sin(_Timer * PI) * (1 - _Timer) * (1 - timer) * radius; half wavefunc = cos(2 * PI * (_Frequency * timer - rad / _WaveMaxLength)); return A * wavefunc; } void vert (inout appdata_full v) { float4 poleParams = tex2Dlod (_PoleTexture, float4(v.texcoord.xy, 0, 0)); v.vertex.z += getHeight(v.vertex.x, v.vertex.y, (poleParams.r - 0.5) * 2, (poleParams.g - 0.5) * 2, poleParams.b , poleParams.a); } void surf (Input IN, inout SurfaceOutputStandard o) { o.Albedo = tex2D(_MainTex, IN.uv_MainTex).rgb * _Color.rgb; o.Normal = UnpackNormal(tex2D(_Normal, IN.uv_MainTex)); o.Metallic = tex2D(_Roughness, IN.uv_MainTex).rgb; o.Occlusion = tex2D(_Occlusion, IN.uv_MainTex).rgb; o.Smoothness = _Glossiness; o.Alpha = _Color.a; } ENDCG } FallBack "Diffuse" }
Le projet dans son ensemble et son fonctionnement se trouvent
ici . Certes, une partie des ressources a dû être supprimée en raison des limites de poids du github (hdr skybox et voiture).
Merci de votre attention! J'espère que l'article sera utile à quelqu'un, et il est devenu un peu plus clair pourquoi la trigonométrie, la géométrie analytique (tout ce qui concerne les courbes) et d'autres disciplines mathématiques peuvent être nécessaires.