Résumé
Une description est donnée des lois qui ont été établies dans une liste séquentielle de toutes les solutions au problème de distribution n-Queens. Il est établi que:
- La proportion de solutions complètes dans la liste générale de toutes les solutions diminue, avec une valeur croissante de n.
- Les solutions complètes sont réparties dans une liste séquentielle de toutes les solutions de manière à ce que les solutions complètes situées les unes à côté des autres dans la liste soient les plus susceptibles d'être trouvées.
- Il y a symétrie dans l'ordre des solutions complètes dans la liste générale de toutes les solutions. Si dans la i-ème position depuis le début de la liste la solution est complète, alors la solution symétrique de la fin de la liste située dans la position n-i + 1 est également complète (la règle de symétrie des solutions).
- Toutes les paires de solutions, à la fois courtes et complètes, situées symétriquement dans la liste de toutes les solutions, sont complémentaires - la somme des indices de position des lignes correspondantes est une constante et égale à n + 1 (la règle de complémentarité des solutions). Cela suggère que seule la première moitié de la liste de toutes les solutions complètes est «unique», toute solution complète de la seconde moitié de la liste peut être obtenue sur la base de la règle de complémentarité. Une conséquence de cette règle est le fait que pour toute valeur de n, le nombre de solutions complètes sera toujours un nombre pair.
- L'activité des cellules des rangées de la matrice de solution est symétrique par rapport à l'axe horizontal passant par le milieu de cette matrice. Cela signifie que l'activité des cellules de la i-ème ligne coïncide toujours avec l'activité des cellules de la ligne n-i + 1. Par activité, on entend la fréquence à laquelle l'index cellulaire se produit dans la ligne correspondante de la liste des solutions complètes. De même, l'activité des cellules des colonnes de la matrice de solution est symétrique par rapport à l'axe vertical divisant la matrice en deux parties égales
- Quel que soit n, dans une recherche séquentielle de toutes les solutions, la première solution complète n'apparaît qu'après une certaine séquence de solutions courtes. La taille de la séquence initiale de solutions courtes augmente avec n. La longueur de la liste des solutions courtes avant l'apparition de la première solution complète pour les valeurs paires de n est significativement plus longue que pour les valeurs impaires les plus proches.
- La ligne de la matrice de décision, sur laquelle les difficultés commencent à avancer et la première décision courte est formée, divise la matrice selon la règle du nombre d'or. Pour les petites valeurs de n, une telle conclusion est approximative, mais avec une augmentation de la valeur de n, la précision d'une telle conclusion augmente asymptotiquement au niveau de la règle standard.
Cette publication présente les principaux résultats de l'article [1] , qui a été publié dans la revue «Modeling of Artificial Intelligence, 2018, 5 (1)». Sur Habré, il y avait des travaux liés à un problème de n-Queens: [2] , [3] ,
Le problème de la distribution de n reines sur un échiquier de taille nxn a une longue histoire. Il a été initialement formulé en 1848 par M. Bezzel [4] comme une tâche intellectuelle pour un échiquier régulier. Au fil du temps, l'énoncé du problème a été élargi par F. Nauck [5], et la taille d'un échiquier pouvait prendre n'importe quelle valeur.
Présentation
L'énoncé du problème est assez simple: vous devez répartir n reines sur un échiquier de taille nxn de sorte que dans chaque ligne, chaque colonne, ainsi que sur les diagonales gauche et droite passant par la cellule où se trouve la reine, il n'y ait pas plus d'une reine. Cette tâche est facile à comprendre ou à expliquer à quelqu'un, mais elle est plutôt difficile à résoudre. Le fait est qu'il n'y a pas de règles sur la base desquelles vous pouvez organiser des reines sur chaque ligne afin d'obtenir une solution. Une solution ne peut être obtenue qu'en énumérant diverses variantes de l'arrangement des reines dans certaines lignes. Cependant, la complexité de cette méthode de solution réside dans le fait que le nombre de toutes les variantes de l'arrangement des reines augmente de façon exponentielle avec l'augmentation de n. De plus, tout pas en avant pour placer la reine dans la position libre d'une certaine ligne entraîne un changement dans la liste des positions libres dans les lignes restantes, et lors du retour d'une étape, afin de former une branche de recherche, il est nécessaire d'effacer les traces des actions précédemment effectuées.
Il existe un grand nombre de publications liées à divers aspects de la résolution du problème des n-reines. Ils peuvent être attribués à plusieurs domaines de recherche: la recherche de toutes les solutions complètes pour une valeur donnée de la taille d'un échiquier (n), le développement d'un algorithme rapide pour trouver une solution pour différentes valeurs de n, la solution du problème complet à une solution complète, pour une composition arbitraire de k reines, des questions la complexité de calcul des calculs algorithmiques, ainsi que diverses modifications de la formulation originale du problème. Pour me familiariser avec ces domaines, je recommanderais des publications intéressantes de B. Jordan, S. Brett [6] et IP Gent, C. Jefferson, P. Nightingale [7], qui fournissent un aperçu assez détaillé de divers domaines de recherche. Il convient de noter en particulier la publication Internet [8] soutenue par Walter Costers, qui a été préparée par un groupe de l'Universiteit Leiden et contient des liens vers 342 publications liées au problème des n-reines (en décembre 2018).
Bien que le problème des n-Queens soit resté actif pendant plus de 150 ans, et qu'un grand nombre de publications ont été publiées pendant cette période, je n'ai pas pu trouver d'emploi qui soit pertinent pour la recherche de modèles dans les résultats de la résolution de ce problème. La plupart des projets liés à la recherche de toutes les solutions n'ont probablement pas sauvegardé les solutions trouvées et ne voyaient pas ce qu'il y avait "à l'intérieur". Dans le cadre de la tâche, il y avait d'autres objectifs dominants, et nos estimés collègues les ont atteints. Cependant, à distance, il me semble que la situation est similaire à celle où une personne fait bouillir des œufs pour le petit déjeuner, mais ne les mange pas, mais les jette, ne laissant que le nombre d'œufs durs dans sa mémoire. J'ai toujours été sûr que si les données ne sont pas aléatoires, il devrait y avoir une certaine régularité en elles, même si nous ne pouvons pas trouver cette régularité. C'est cette conviction qui a motivé la recherche de modèles dans cette tâche.
Parallèlement au désir de fournir aux membres de la communauté Habr des informations utiles à la réflexion, j'aimerais que des programmeurs talentueux, dont la plupart sur Habr, accordent plus d'attention à une direction de développement telle que la simulation par ordinateur (simulation informatique). En tant que méthode de recherche, de telles «mathématiques algorithmiques» sont utilisées à la «pointe» de nombreux domaines: intelligence artificielle, science des logiciels, science des données, ... et je suis sûr que des problèmes très complexes et importants pour une application pratique seront résolus sur la base des mathématiques algorithmiques. sinon.
Définitions
Ci-après, nous désignerons la taille de l'échiquier par le symbole n. Une solution sera dite complète si toutes les n reines sont placées de manière cohérente sur un échiquier. Toutes les autres solutions, lorsque le nombre de reines correctement placées est inférieur à n - nous appellerons des solutions courtes. Par la longueur d'une solution, nous entendons le nombre (k) de reines correctement placées. Le nombre de toutes les solutions, pour une valeur donnée de n, sera noté m. Comme analogue d'un «échiquier» de taille nx n., Nous considérerons une «matrice de solution» de taille nx n.
Commencer
Afin de mener une étude, un algorithme a été développé pour rechercher toutes les solutions pour une valeur arbitraire de n. Nous n'avons pas utilisé la récursivité standard ou le système habituel de boucles imbriquées. Pour de grandes valeurs de n, cette approche serait assez problématique. L'algorithme a été construit sur la base d'un ensemble d'événements en interaction, dans chacun desquels un certain système d'actions se déroule, interconnecté. Cela permet d'implémenter simplement le mécanisme de changement de l'espace d'états lors du choix du nœud suivant dans la branche de la solution du problème (suivi Forward), ou d'effacer les traces d'actions précédemment effectuées, lors du retour d'une ou plusieurs étapes (Back Tracking). Il n'y a pas d'exigences particulières pour la taille de la mémoire ou la vitesse du processeur dans l'algorithme.
Sur la base de cet algorithme, toutes les solutions séquentielles (à la fois courtes et complètes) pour diverses valeurs de la matrice de solutions n = (7, ..., 16) ont été trouvées. Comme la taille de la liste des solutions complètes est la séquence nommée l' Encyclopédie en ligne des séquences entières (séquence A000170 [9]) et est indiquée dans de nombreuses publications, il me semble intéressant de lister la taille de la liste de toutes les solutions (courte + complète) pour les valeurs de n considérées par nous: 7 (194), 8 (736), 9 (2 936), 10 (12 774), 11 (61076), 12 (314 730), 13 (1 716 652), 14 (10 030 692), 15 ( 62 518 772), 16 (415 515 376).
De plus, en utilisant les solutions trouvées, nous donnons le libellé de certains problèmes, les méthodes pour les résoudre et une description des résultats.
1. L'espace d'état dans lequel les solutions sont recherchées
L'énumération de diverses options pour l'arrangement des reines dans certaines rangées d'une matrice d'une décision de taille n conduit à la formation d'un espace d'états. S'il n'y avait aucune interdiction sur l'arrangement des reines dans l'une ou l'autre cellule de la matrice, alors la taille de l'espace d'état serait n n . Si nous ne prenons en compte que la règle interdisant l'emplacement de plus d'une reine dans chaque ligne et chaque colonne, nous obtenons alors un sous-ensemble de l'espace d'état, dont la taille sera égale à n! Ce sous-ensemble de l'espace d'état correspond au problème de la distribution de n par la tour. Si, en plus de cela, nous prenons également en compte la règle interdisant l'emplacement de plus d'une reine sur les diagonales gauche et droite passant par la cellule où se trouve la reine, alors nous obtenons un espace de recherche dont la taille sera inférieure à n! .. Nous appelons un tel sous-ensemble de l'espace d'état - un espace de recherche productif, basé sur le fait que ce n'est que dans ce sous-espace que toutes les solutions sont possibles. Toutes les branches terminées dans l'espace de recherche productif sont des solutions avec un certain nombre de reines correctement placées. Fondamentalement, ce sont des décisions courtes, et seule une petite partie restante sont des décisions complètes.
La figure 1 montre des graphiques du logarithme naturel de trois indicateurs: a) la valeur factorielle (n!) Sur la taille de la matrice de décision; b) le nombre de toutes les décisions (à la fois courtes et complètes); c) le nombre de solutions complètes, en fonction de la taille de la matrice de solutions (n). Comme prévu, toutes les courbes sont caractérisées par une augmentation exponentielle avec l'augmentation de n. Les taux de croissance du nombre de toutes les solutions et du nombre de solutions complètes diffèrent, bien que cela ne soit pas si visible sur le graphique, en raison de la petite taille de l'échantillon de n valeurs. Par exemple, pour n = 13, la différence entre les logarithmes de ces indicateurs est de 3,148, et pour n = 16, cette différence augmente de 0,190 et est de 3,338. De toute évidence, avec une nouvelle augmentation de n, cet écart sera plus important.

Fig.1 Dépendance du logarithme de la taille de l'espace d'état sur la valeur n
2. Comment la proportion de décisions complètes dans la liste générale de toutes les décisions change-t-elle?
De toute évidence, si le taux de croissance du nombre de solutions complètes est en retard sur le taux de croissance du nombre de toutes les solutions, la probabilité de trouver une solution complète dans la liste générale de toutes les solutions diminuera avec l'augmentation de la valeur de n. La figure 2 montre un graphique de la proportion de solutions complètes dans la liste générale de toutes les solutions sur la valeur de n. On voit qu'avec une augmentation de la taille de la matrice de solutions, la part de toutes les solutions complètes dans la liste générale diminue. Pour les valeurs initiales n = (7, ..., 14), cette valeur diminue 5,66 fois de la valeur 0,2062 à 0,0364, puis une diminution progressive et asymptotique de cette valeur se poursuit. Ici, une contradiction formelle survient entre deux affirmations: d'une part, le nombre de solutions complètes augmente exponentiellement avec l'augmentation de n, et d'autre part, la probabilité d'une solution complète dans une liste séquentielle de toutes les solutions diminue constamment. Ce paradoxe apparent s'explique très simplement, la taille de l'espace productif et la taille associée de la liste de toutes les solutions croît plus vite avec l'augmentation de n que le nombre de solutions complètes. C'est comme essayer de trouver une aiguille dans une botte de foin - la quantité de foin "avec n croissant" augmente plus rapidement que le nombre d'aiguilles qui y sont perdues. Par conséquent, nous pouvons supposer que si pour n = 27, le nombre de solutions complètes est d'environ 2,346 * 10 17 , alors la valeur correspondante du nombre de toutes les solutions sera très probablement de 3 à 4 ordres de grandeur supérieure à ~ 10 20
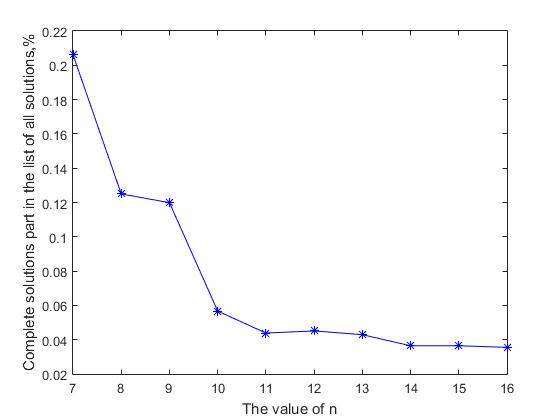
Fig.2 Diminution de la proportion de solutions complètes dans la liste générale de toutes les solutions avec n croissant
3. Quelle est la fréquence des solutions de différentes longueurs dans la liste de toutes les solutions?
Comme mentionné précédemment, toutes les branches terminées dans l'espace de recherche productif sont des solutions avec un nombre différent de reines correctement placées.
Il nous intéresse avec quelle fréquence il y a des solutions de différentes longueurs dans la liste générale de toutes les solutions.
Le tableau 1 pour les valeurs n = (7, ..., 12) présente les valeurs correspondantes des fréquences relatives pour des solutions de longueurs différentes. La représentation visuelle correspondante de ces données est illustrée à la figure 3.
L'analyse du tableau nous permet de tirer les conclusions suivantes:
a) pour chaque matrice de taille n, il existe une certaine longueur de la solution qui a une fréquence maximale (mise en évidence en gras).
Tableau 1. Fréquence relative (%) de solutions de longueurs différentes (k) pour une matrice de taille n = (7, ..., 12)
| n \ k | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|
| 7 | 10,31 | 31.23 | 27,84 | 20,62 | | | | | |
| 8 | 2,45 | 20,38 | 34,78 | 29,89 | 12,50 | | | | |
| 9 | 0,34 | 5.79 | 21,73 | 35,83 | 34,32 | 11,99 | | | |
| 10 | 0,05 | 1,35 | 8.41 | 25,62 | 32,94 | 25,96 | 5.67 | | |
| 11 | | 0,15 | 2.12 | 11.80 | 26,71 | 34,47 | 20,36 | 4.39 | |
| 12 | | 0,01 | 0,29 | 3.28 | 13,56 | 29,88 | 31,29 | 17.18 | 4.51 |
b) lorsque n augmente, le nombre de solutions de longueurs différentes augmente. En conséquence, la fréquence relative de toutes les décisions diminue.
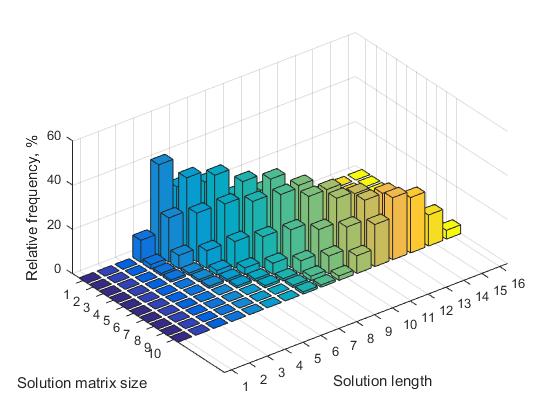
Fig.3 Fréquence des solutions de différentes longueurs en fonction de la taille de la matrice de solution, n = 7, ..., 16
c) pour chaque matrice de taille n, il existe une certaine taille minimale de la longueur de la solution, en dessous de laquelle les solutions courtes ne se produisent pas. Lorsque n augmente, la valeur de ce seuil augmente. Par exemple, pour n = 8, la valeur de seuil est 4, respectivement, pour n = 16, la valeur de seuil est 7.
4. Quelle est la disposition relative des solutions complètes dans une liste séquentielle de toutes les solutions?
Dans l'énoncé du problème "sur la distribution de n reines", il n'y a pas de raisons qui permettraient de faire des hypothèses sur la séquence des décisions complètes dans la liste générale de toutes les solutions. Nous voulions savoir si les solutions complètes de la liste générale sont distribuées de manière uniforme, aléatoire ou si elle présente des particularités. Pour le savoir, nous avons analysé les distances entre les solutions complètes les plus proches dans une liste séquentielle de toutes les solutions. Comme le montre la figure 4, où pour n = 12, un graphique des changements dans les fréquences correspondantes est présenté,
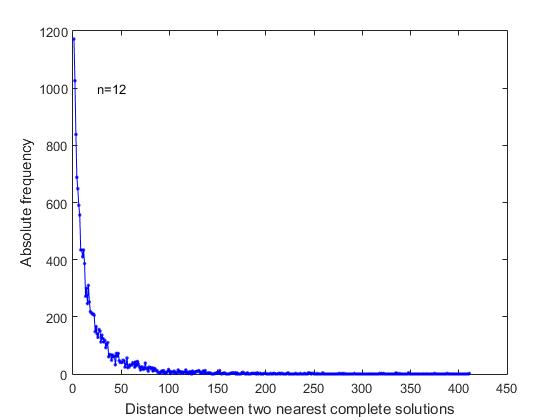
Fig.4 Fréquence en fonction de la distance entre les solutions complètes les plus proches dans une liste séquentielle de toutes les solutions complètes (n = 12)
avec la plus grande fréquence, il existe des solutions complètes qui se succèdent immédiatement dans une liste séquentielle commune de toutes les solutions. Ce sont les cas de la formation de la branche de recherche lorsque la relation des positions libres dans les dernières lignes vous permet de former deux ou plusieurs solutions complètes consécutives. De plus, la fréquence maximale sont les solutions complètes entre lesquelles se trouvent: une solution courte, deux solutions courtes, etc.
5. Y a-t-il un schéma dans la disposition des solutions complètes dans la liste générale de toutes les solutions?
Pour répondre à cette question, nous avons analysé des listes séquentielles de toutes les solutions pour les valeurs n = (7, ..., 16). Pour démontrer clairement les résultats, dans la figure 5, pour la valeur n = 8, un graphique est présenté où la longueur de chaque solution dans la liste des 736 solutions est successivement indiquée. Ici, seules 92 solutions sont complètes et elles sont surlignées en rouge, les 644 solutions restantes sont courtes et surlignées en bleu. On peut voir que les solutions complètes ne sont pas réparties uniformément dans la liste de toutes les solutions. Il y a des domaines où les solutions complètes sont plus courantes et il y a des endroits où les solutions complètes sont rares ou pas du tout.

Fig. 5 La longueur de chaque solution dans une liste séquentielle de toutes les solutions, pour une matrice 8 x 8 (rouge - solutions complètes, bleu - solutions courtes). Le nombre total de toutes les solutions est de 736
Cependant, quelque chose d'autre est important ici. Si vous regardez attentivement l'image ressemblant à un code-barres bleu-rouge, vous remarquerez une caractéristique très importante, toutes les lignes rouges sont symétriques par rapport à une ligne verticale conditionnelle passant par le milieu de la liste des solutions. , , i- , , m-i+1. , n=8, , 43- , , 736- 43 +1=694. 17- 10x10 368- , 12774-17+1=12407. . . n, , i- , , m-i+1 ( ). m, , . , n, , . ( – ).
, – . n+1 . , 17- n=10 368- (1, 5, 7, 10, 4, 2, 9, 3, 6, 8).
, 12407 (10, 6, 4, 1, 7, 9, 2, 8, 5, 3). , (11, 11, …,11). n, , , . . n, ( , ), , – n+1 ( ). Q(i ) Q1(i) – ,
<b>`Q ( i ) + Q1 ( i ) = n + 1, i = (1, n) `</b>
Cette règle signifie que si une solution complète est obtenue à la i- ème étape, alors la solution complète symétrique à l'étape m - i +1 devient connue . Par conséquent, lors de la recherche de toutes les solutions complètes, il suffit de ne trouver que la première moitié de toutes les solutions complètes. La seconde moitié de la liste des solutions complètes peut être déterminée à partir des solutions déjà obtenues, sur la base de la règle de complémentarité. Le critère pour atteindre la moitié de la liste des solutions complètes est le respect de la règle de complémentarité entre la solution complète précédente Q (i-1) et la Q suivante (i) . c'est-à-dire qu'il est nécessaire que la somme de chaque paire d'indices correspondants de deux solutions consécutives soit égale à n + 1 . Étant donné que toute solution complète de la liste de toutes les solutions complètes est unique, seules les solutions complètes consécutives seront complémentaires qui se trouvent des deux côtés de la frontière qui divise la liste en deux.
Ces deux règles permettront à l'avenir, lors de la recherche de toutes les solutions complètes pour toute valeur suivante de n, de réduire de moitié le temps de calcul et, par conséquent, le temps de calcul.
6. Visualisation de la séquence d'étapes pour trouver la première solution complète
Comment se déroule le processus d'avance (suivi vers l'avant) et de retour (suivi vers l'arrière) lors de la création d'une branche d'une recherche de solution? Afin de répondre à cette question, nous avons, pour une matrice 10 x 10, déterminé la séquence des 194 transitions initiales entre les lignes jusqu'à l'apparition de la première solution complète. Le graphique correspondant est illustré à la figure 6. Les lignes bleues indiquent un mouvement vers l'avant et les lignes rouges indiquent un retour. Au cours de ces 194 étapes, 35 solutions courtes ont été créées. La figure montre que la plupart des transitions (84,5%) se produisent entre les lignes (5, 6, 7, 8). Il s'agit d'une sorte de «goulot d'étranglement» sur le chemin du «but». Comme le montre la figure, il n'y a que 7 cas de passage à la 4ème ligne et un cas de passage à la troisième ligne. Il y a également 13 cas de passage à la 9e ligne. Trois tentatives pour passer à la 10e ligne ont échoué, car dans ces branches de recherche sur la 10e ligne il n'y avait pas de position vide. Cet exemple montre toutes les branches de court

Fig. 6 Visualisation des événements Backtracking (rouge) et Forwardtracking (bleu) pour les 194 premières étapes de recherche (n = 10)
jusqu'à la première solution complète. Tout algorithme pour résoudre un tel problème sera efficace s'il contient un mécanisme qui éliminera tout (ou une partie) des branches qui mènent à des solutions courtes.
7. Après combien de décisions brèves la première solution complète apparaît-elle?
Étant donné que les solutions complètes apparaissent différemment sur différentes parties de la liste de toutes les solutions, il semble important de savoir dans combien de solutions courtes la première solution complète apparaît lors de la recherche séquentielle de toutes les solutions. Pour cela, pour les valeurs n = (7, ..., 35), toutes les solutions courtes ont été successivement calculées jusqu'à l'apparition de la première solution complète. Comme le montre la figure 7, qui montre un graphique de la dépendance à n, le logarithme naturel du numéro d'étape, lorsque la première solution complète est apparue, pour les valeurs paires de n, la première solution complète apparaît beaucoup plus tard que pour les valeurs impaires les plus proches de n. Par exemple, pour une valeur impaire n = 21, la première solution complète apparaît à l'étape 3138, et pour la valeur paire suivante n = 22, la première solution complète apparaît à l'étape 628169. Par conséquent, pour la prochaine valeur impaire n = 23, la première solution complète apparaît à l'étape 9155.

Fig.7 Le nombre de solutions courtes jusqu'à la première solution complète, pour différentes valeurs de n
Le nombre d'étapes d'itération pour pair n = 22 est respectivement 200,2 et 68,6 fois supérieur aux valeurs impaires les plus proches. Cela est particulièrement évident dans le temps de comptage pour n = 34. Ici, la première solution complète apparaît à 826 337 184e étapes, et pour les nombres impairs les plus proches (33, 35), respectivement, à 50 704 900e et 84 888 759e étapes. Il faut aussi dire sur la violation de la croissance monotone du nombre de solutions courtes avant l'apparition de la première solution complète, avec l'augmentation de n. Pour les valeurs paires de n, cela se produit à n = 19, pour les valeurs impaires, à n = 24 et n = 26.
8. La fréquence des cellules de chaque ligne de la liste de toutes les solutions complètes est-elle la même?
La matrice de décision de taille nxn, qui sert d'analogue à un échiquier, est comme une scène sur laquelle tous les événements ont lieu. Toute solution complète formée sur cette scène se compose d'indices de cellules de différentes lignes, car chacune de ces cellules est un nœud dans la branche de recherche de solution. La question qui nous intéressera est la suivante: la charge dans chaque ligne est-elle la même pour différentes cellules lors de la formation d'une liste de toutes les solutions complètes? De toute évidence, plus la valeur de fréquence est élevée, plus l'activité de cette cellule dans la formation d'une liste de solutions complètes est élevée. Pour l'établir, nous déterminons pour chaque ligne, à partir d'une liste de toutes les solutions complètes, la fréquence relative des différents indices. Tout d'abord, nous analysons une matrice de solution de taille n = 8. Examinons séquentiellement chaque ligne du tableau de solutions complètes et déterminons la fréquence des différentes valeurs d'index. Le tableau 2 montre les valeurs correspondantes des fréquences d'activité absolue de différentes cellules dans chacune des huit rangées, et sur la Fig. 8
Tableau 2. Fréquence absolue de l'activité cellulaire dans chacune des huit lignes de la matrice de décision 8x8, basée sur une analyse de la liste de toutes les solutions complètes
| ligne \ col | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|
| 1 | 4 | 8 | 16 | 18 | 18 | 16 | 8 | 4 |
| 2 | 8 | 16 | 14 | 8 | 8 | 14 | 16 | 8 |
| 3 | 16 | 14 | 4 | 12 | 12 | 4 | 14 | 16 |
| 4 | 18 | 8 | 12 | 8 | 8 | 12 | 8 | 18 |
| 5 | 18 | 8 | 12 | 8 | 8 | 12 | 8 | 18 |
| 6 | 16 | 14 | 4 | 12 | 12 | 4 | 14 | 16 |
| 7 | 8 | 16 | 14 | 8 | 8 | 14 | 16 | 8 |
| 8 | 4 | 8 | 16 | 18 | 18 | 16 | 8 | 4 |
un groupe de 4 graphiques est présenté, où chaque graphique caractérise le changement de fréquences relatives sur une ligne. L'une des conclusions fondamentalement importantes que l'on peut tirer de l'analyse de toutes les données obtenues est la suivante:
- pour une matrice de décision de taille arbitraire n , l'activité des cellules de la i- ème ligne coïncide avec l'activité de la cellule n-i + 1 , c'est-à-dire l'activité des cellules de la première ligne coïncide toujours avec l'activité des cellules de la dernière ligne, respectivement, l'activité des cellules de la deuxième ligne coïncide avec l'activité des cellules de l'avant-dernière ligne, etc.
Si n est impair, seule la ligne médiane de la matrice de solution n'a pas de paire symétrique; pour toutes les autres cellules, la règle ci-dessus est valide - Nous appelons cela la «propriété de symétrie horizontale de l'activité des cellules des différentes rangées de la matrice de solution» . Pour cette raison, nous n'avons présenté que 4 graphiques pour la matrice de décision de taille n = 8, car les graphiques correspondants de l'activité cellulaire pour les lignes (1, 8), (2.7), (3.6) et (4.5) sont complètement identiques.
Il convient également de noter que les valeurs de fréquence sont symétriques par rapport à l'axe vertical divisant la matrice en deux parties égales (dans le cas d'une valeur paire de n), ou passant par la colonne médiane (dans le cas d'une valeur impaire de n). Nous appelons cela la «propriété de symétrie verticale de l'activité des cellules des différentes rangées de la matrice de solution» .
De plus, comme il ressort de l'analyse du tableau 2, les fréquences dans la matrice de solution sont symétriques par rapport aux diagonales principales gauche et droite.
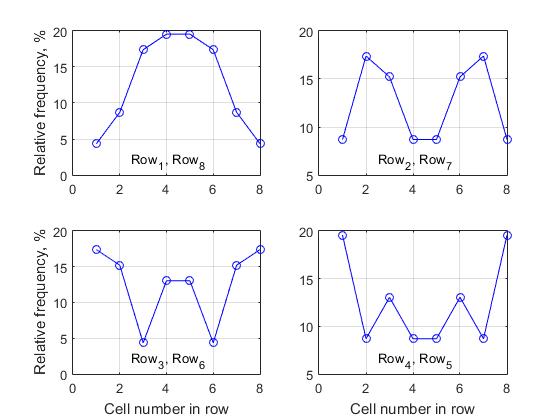
Fig.8 Activité cellulaire des rangées correspondantes lors de la formation de la liste des solutions complètes, n = 8
Je pense que la présence de règles restrictives dans l'énoncé du problème, et la propriété connexe du non-déterminisme, «forment» une sorte de relation harmonieuse entre les nœuds de lignes différentes. Les branches de la recherche qui correspondent à ces règles - conduisent à la formation d'une solution complète. Les branches restantes de la recherche, à un moment donné, violent ces règles et, par conséquent, «achèvent leur voyage» sous la forme de décisions brèves. Il convient de noter ici que les cellules de la matrice de décision n'ont qu'une relation locale au sein du groupe d'influence de projection, il n'y a pas de règles prescrites pour des actions coordonnées entre elles. L'activité collective des cellules n'est qu'une conséquence du résultat de l'influence de règles restrictives. Par conséquent, une question plutôt intéressante reste ouverte, comment les règles restrictives, comme les facteurs non déterministes, affectent les cellules de la matrice de décision, ce qui conduit finalement à la formation d'une matrice d'activité cellulaire «harmonieuse» - symétrique par rapport aux axes horizontal et vertical, ainsi que par rapport à la gauche et diagonales principales droites. Est-ce une propriété caractéristique de ce problème uniquement, ou vaut-il également pour d'autres problèmes non déterministes?
9. À partir de quel numéro de ligne l'algorithme de suivi avant - suivi arrière est-il activé?
Si nous suivons le fonctionnement de l'algorithme de sélection de ligne séquentielle dans la matrice de décision pour l'emplacement de la reine, nous pouvons voir qu'à partir d'une certaine ligne, que nous appellerons «StopRow», le processus d'avancement est «freiné». Dans la branche de recherche, c'est la première ligne où il y a des problèmes avec la disponibilité de

Fig. 9-1 Dépendance du rapport de l'indice StopRow à n sur la taille de la matrice de décision (partie 1)
position pour l'emplacement de la reine. C'est à partir de cette ligne que l'algorithme de suivi arrière est activé pour effacer les traces des actions précédemment effectuées et revenir en arrière. C'est la ligne sur laquelle apparaît la première solution courte.
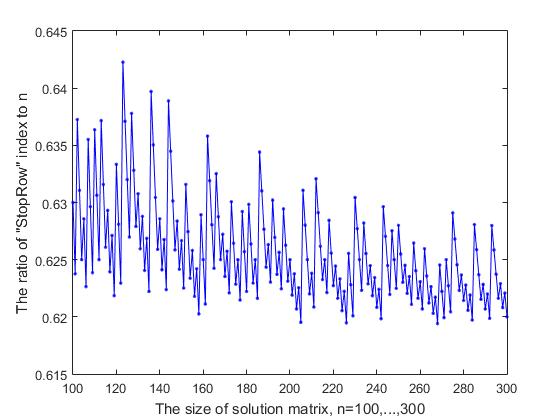
Fig. 9-2 Dépendance du rapport de l'indice StopRow à n sur la taille de la matrice de décision (partie-2)
L'indice de la ligne «StopRow», avec lequel les difficultés commencent à avancer, dépend de la taille n de la matrice de décision. Si nous considérons le rapport de cet indice, que nous désignons par StopInd à la taille de la matrice de solution n, alors, comme le montre la figure 9-1, où les résultats du calcul pour les valeurs initiales n = (7, ..., 99) sont présentés, ce rapport fluctue dans une mesure plus ou moins grande côté et a tendance à diminuer. Avec une augmentation de n = (100, ..., 300), ce rapport oscille entre 0,619 - 0,642 (Fig.9-2), et avec une nouvelle augmentation de n, nous obtenons les résultats suivants (les valeurs de n sont données en séquence et la valeur entre parenthèses est Rapport StopInd et StopInd / n: 1000 (619, 0,6190), 2000 (1239, 0,6195), 3000 (1856, 0,6187), 4000 (2473, 0,6182), 5000 (3091, 0,6182). -line divise la matrice de décision selon la règle du nombre d'or : à savoir, le rapport StopInd / n diffère de (n-StopInd) / StopInd d'une petite quantité qui tend vers zéro avec l'augmentation de n. Par exemple, pour n = 5000, la différence entre les relations 3091/5000 et 1909/3091 est 0,006, ce qui représente moins de 0,1% de la moyenne de ces deux relations.
Le graphique représenté sur les deux figures 9- (1,2) présente une forme de variabilité non aléatoire, qui ressemble à un enregistrement sur une «portée musicale». Des sauts répétés et des chutes par étapes sont visibles avec une périodicité irrégulière. De toute évidence, il existe une raison à ce type de comportement de courbe, et cela sera peut-être intéressant pour la recherche. Pour cette raison, dans un but de visualisation plus détaillée, le graphique a été présenté en deux figures.
Je n'ai considéré qu'une partie des questions qui peuvent être formulées à partir des résultats de la solution du problème "sur la distribution des n-reines". J'espère que les résultats obtenus rendront les mécanismes de la formation de processus non déterministes et les changements dans l'espace d'état plus transparents pour la compréhension. Peut-être que cela servira de point d'appui pour la formulation de nouvelles tâches et pour aller de l'avant.
Conclusion
- Si, en regardant la publication, nous sommes parvenus à une conclusion, alors naturellement la question se posera: "que signifie la solution du problème d'un milliard de reines dans le titre de l'article?" En préparant la publication pour Habr, j'ai pensé qu'une personne qui a, par exemple, une mine où les diamants sont extraits, devrait donner au moins un diamant chacun à ses amis et parents, sinon ce serait injuste. Par conséquent, je voudrais offrir un cadeau à tous les membres de la communauté habr: participants, organisateurs, visiteurs. Comme son nom l'indique, c'est la solution au problème de la distribution d'un milliard de reines sur un échiquier d'un milliard de milliards de dollars.
Bien sûr, ce n'est pas un diamant à facettes, mais pour les vrais connaisseurs de l'art intellectuel, il peut être plus précieux que "une sorte de diamant là-bas". De plus, les diamants sont très différents à travers le monde, et cette solution n'est pour l'instant qu'en un seul exemplaire. Et notre Byte-God (*) voit que je le fais sincèrement.
La solution qui en résulte est un tableau unidimensionnel d'un milliard de nombres, qui est présenté au format MatLab .mat et est disponible sur: One Billion Queens Problem Solution sur Google Drive
-Le premier élément de ce tableau caractérise la position de la reine dans la première ligne, le deuxième élément - la position dans la deuxième ligne, etc. Ce n'est qu'une solution parmi les milliards de solutions possibles. Et la valeur de nBillion est si grande qu'elle peut être considérée comme un proche parent de l'infini.
- Il me semble que cette solution peut être attribuée à la catégorie des valeurs intellectuelles virtuelles. On peut dire que "c'est quelque chose dans lequel il y a quelque chose". Ils ne peuvent vraiment pas être «touchés», donc ils ne sont perçus dans la conscience qu'au niveau des sensations. Là, en fait, il y a un ordre étonnant et une harmonie explicite et implicite. Il s'agit d'un cadeau purement symbolique (au sens propre et figuré) qui s'adresse à tous les membres de la communauté. Je pense: " Vous n'êtes pas comme tout le monde ."
(J'espère que quelqu'un «ramènera le cadeau à la maison». Le fichier est assez volumineux - 3,7 Go. Il s'agit de données propres et vérifiées. Que Google Drive affichera des avertissements - traitez-le avec compréhension)
- Avant de prendre cette décision, j'ai réfléchi à la nature individuelle et collective d'un tel cadeau. Est-il possible que l'un soit présenté avec l'original et le reste avec des copies? Mais la solution était simple. Les concepts habituels «quotidiens» de «original» et de «copie», dans ce cas, perdent leur sens. Nous ne copions pas, mais créons un autre original. Et les «originaux» sont les mêmes pour tous et également équivalents.
- Je pense qu'en compagnie de parents, vous serez très probablement le seul à avoir reçu un tel «produit intellectuel» en cadeau. Ce sera amusant si vous parlez à votre belle-mère d'un tel cadeau: "Imaginez un échiquier de maman mesurant 50 000 km sur 50 000 km, sur lequel 1 milliard de reines sont réparties de telle manière que l'une ne voit pas l'autre de près ...". Qui sait, peut-être après cela, le gendre sera plus apprécié, car il reçoit un cadeau si étrange.
Je souhaite à tous les membres de la communauté habr santé, succès et bien-être. Puisse la nouvelle année porter chance à nous tous.
(*) - Puisqu'il fait référence au nom de l'objet, sa description doit également être donnée.
Byte Dieu signifie une entité multidimensionnelle, composée de zéros et de uns, raisonnable dans tous les sens et infinie dans toutes les directions. Toute séquence de zéros et de uns dans cet espace représente une certaine connaissance.
Les références
[4] Max Bezzel, Proposition du problème des 8 reines ", Berliner Schachzeitung, Volume
3 (1848), page 363. (Soumis sous le nom d'auteur \ Schachfreund ".)
[5] Franz Nauck, Briefwechseln mit allen fur alle ", Illustrirte Zeitung, Volume
377 Numéro 15 (1850), page 182.
[6] Bell Jordan; Stevens Brett (2009). "Une enquête sur les résultats connus et les domaines de recherche pour les n-reines." Mathématiques discrètes. 309 (1): 1–31
[7] Gent, Ian P.; Jefferson, Christopher; Nightingale, Peter (août 2017). "Complexité de l'achèvement de n-Queens". Journal of Artificial Intelligence Research. AAAI Press. 59: 815–848
[8] W. Kosters and all, n-Queens - 342 références, (20 novembre 2018)
[9] NJA Sloane, l'Encyclopédie en ligne des séquences entières, publiée par voie électronique. 2016