Modèles mathématiques du chaos

Présentation

Habr a déjà discuté de la théorie du chaos dans des articles [1,2,3]. Les aspects suivants de la théorie du chaos sont examinés dans ces articles: schéma généralisé du générateur de Chua; modélisation de la dynamique du système de Lorentz; attracteurs programmés par circuits intégrés logiques Lorentz, Ressler, Rikitake et Nose-Hoover.

Cependant, les techniques de la théorie du chaos sont également utilisées pour modéliser des systèmes biologiques, qui, sans aucun doute, sont l'un des systèmes les plus chaotiques de tous ceux que l'on puisse imaginer. Des systèmes d'égalisation dynamique ont été utilisés pour tout modéliser, de la croissance démographique et épidémique aux battements cardiaques arythmiques [4].

En fait, presque tout système chaotique peut être modélisé - le marché des valeurs mobilières génère des courbes qui peuvent être facilement analysées à l'aide d'étranges attracteurs, le processus de chute des gouttes d'un robinet qui fuit est aléatoire lorsqu'il est analysé à l'oreille nue, mais s'il est présenté comme un étrange attracteur, il s'ouvre un ordre surnaturel qui ne pouvait être attendu des moyens traditionnels.

Le but de cet article est de considérer la théorie du chaos en utilisant l'exemple de l'augmentation du nombre de populations biologiques et du doublement du cycle dans les systèmes mécaniques avec la visualisation graphique de modèles mathématiques basés sur des programmes simples et intuitifs écrits en Python.

L'article a été écrit dans le but d'enseigner, mais permettra même à un lecteur sans expérience en programmation d'utiliser les programmes ci-dessus pour résoudre de manière indépendante la plupart des nouveaux problèmes éducatifs sur le thème de la modélisation des phénomènes de chaos.

Doubler la période des cycles et du chaos sur l'exemple de la croissance du nombre de populations biologiques

Commençons par examiner l'équation différentielle logistique qui modélise une augmentation limitée plutôt qu'exponentielle du nombre de populations biologiques:

$$$\ frac {dN} {dt} = aN-bN ^ {2}, (a, b> 0). (1)$

C'est cette équation qui peut prédire des modèles de comportement exotiques et inattendus de certaines populations. En effet, selon (1), pour $$$t \ rightarrow + \ infty$ la taille de la population s'approche de la frontière égale à a / b .

Pour la solution numérique de la solution différentielle logistique, vous pouvez utiliser l'algorithme le plus simple, avec la valeur numérique du pas de temps, en prenant $$$t_ {n + 1} = t_ {n} + h$ , alors la solution (1) peut être obtenue en appliquant à plusieurs reprises la relation suivante:

$$$N_ {n + 1} = N_ {n} + (aN_n-bN {_ {n}} ^ {2}) h.$ (2)

Nous représentons l'équation (2) sous la forme d'une équation logistique en différences finies:

$$$N_ {n + 1} = rN_ {n} -sN {_ {n}} ^ {2}$ . (3)

où: r = 1 + ah et s = bh .
Remplacement en (3) $$$N_ {n} = \ frac {r} {s} x_ {n}$ on obtient la formule itérative:

$$$x_ {n + 1} = rx_ {n} (1-x_ {n})$ , (4)

En calculant les valeurs données par la relation (3), nous pouvons générer une séquence $$$x_ {1}, x_ {2}, x_ {3}, .....$
les valeurs maximales du nombre de populations que l'environnement supportera à des moments donnés $$$t_ {1}, t_ {2}, t_ {3}.$ .

Nous supposons qu'il existe une valeur limite de fractions exprimant une partie de la taille de la population:

$$$x _ {\ infty} = \ lim_ {n \ to \ infty} x_ {n}$ , (5).

Nous étudierons comment cela dépend $$$x _ {\ infty}$ du paramètre de croissance r dans l'équation (4). Pour ce faire, en Python, nous écrivons un programme qui, en commençant par $$$x_ {1} = 0,5$ calcule les résultats à plusieurs centaines d'itérations ( n = 200 ) pour r = 1,5; 2,0; 2,5 :


Le résultat du programme (pour réduire la sortie des résultats, les trois premières et les quatre dernières valeurs sont données):

  nr=1,5 r=2,0 r=2,5 0 0.5000 0.5000 0.5000 1 0.3750 0.5000 0.6250 2 0.3516 0.5000 0.5859 . . . 197 0.3333 0.5000 0.6000 198 0.3333 0.5000 0.6000 199 0.3333 0.5000 0.6000 200 0.3333 0.5000 0.6000 

Une analyse du modèle discret montre que pour r = 1,5; 2,0; 2,5 avec une augmentation du nombre d'itérations, la valeur $$$x_ {n}$ se stabilise et devient presque égal à la limite $$$x _ {\ infty}$ , qui est déterminé par la relation (5). De plus, pour les valeurs données de r, la quantité $$$x _ {\ infty}$ en conséquence égal $$$x _ {\ infty} = 0,3333; 0,5000; 0,6000$ .
Nous augmentons r = 3,1; 3,25; 3,5 et le nombre d'itérations n = 1008, pour cela nous apportons les modifications suivantes au programme:


Le résultat du programme (pour réduire la sortie des résultats, les quatre premières et huit dernières valeurs sont données):

  nr=3,1 r=3,25 r=3,5 0 0.5000 0.5000 0.5000 1 0.7750 0.8125 0.8750 2 0.5406 0.4951 0.3828 3 0.7699 0.8124 0.8269 . . . 1000 0.5580 0.4953 0.5009 1001 0.7646 0.8124 0.8750 1002 0.5580 0.4953 0.3828 1003 0.7646 0.8124 0.8269 1004 0.5580 0.4953 0.5009 1005 0.7646 0.8124 0.8750 1006 0.5580 0.4953 0.3828 1007 0.7646 0.8124 0.8269 

Comme il ressort des données ci-dessus, au lieu de se stabiliser près d'une seule population limitante, la partie fractionnaire de la population oscille entre deux fractions à mesure que le temps change. Par rapport à r = 3,1 , la période de cycle pour r = 3,25 double et pour r = 3,5 quatre fois.


Le résultat du programme:



En raison du doublement de la période d'itération, $$$x_ {n + 1} = rx_ {n} (1-x_ {n})$ est devenu largement connu. Lorsque la valeur du taux de croissance dépasse r = 3,56 , le doublement de la période s'accélère et un chaos extrême se produit déjà au point r = 3,57 . Pour afficher le début du chaos, nous utilisons le programme suivant:


Le résultat du programme:

  nr=3,57 1000 0.4751 1001 0.8903 1002 0.3487 1003 0.8108 1004 0.5477 1005 0.8844 1006 0.3650 1007 0.8275 1008 0.5096 1009 0.8922 1010 0.3434 1011 0.8050 1012 0.5604 1013 0.8795 1014 0.3784 1015 0.8397 

Nous allons écrire un programme pour visualiser la dépendance du comportement d'itération sur le paramètre de croissance r . Pour chaque valeur de r dans l'intervalle $$$a \ leqslant r \ leqslant b$ 1000 itérations sont effectuées pour atteindre la stabilité. Ensuite, toutes les 250 valeurs obtenues à la suite d'itérations sont tracées le long de l'axe vertical, formant des points ( r, x ):


Le résultat sous forme de diagramme:



Le graphique résultant est appelé un «diagramme de branche» , qui vous permet de déterminer si une valeur r donnée correspond à un cycle ou au chaos. La seule valeur de la taille de la population est déterminée par la valeur $$$r \ environ 3$ puis un cycle d'une période de 2 à $$$r \ environ 3,4$ , puis un cycle avec une période de 4, puis un cycle avec une période de 8 en avant avec une approche rapide du chaos.

Il convient de noter que les zones verticales de l'espace non rempli sur le graphique sont les régions r = 3,6 et r = 3,7 , entre r = 3,7 et r = 3,8 , entre r = 3,8 et r = 3,9 où l'ordre cyclique revient du chaos précédent.
Considérer l'apparition d'un cycle avec une période multiple de 3 dans la région $$ apporter des modifications au programme précédent:


Le résultat du programme:



Le cycle de la période 3 apparaît au voisinage du point r = 3,83 , puis il est divisé séquentiellement en cycles 6,12,24. L'existence d'un cycle de période 3 implique la présence de cycles de toute autre période finie, ainsi que de cycles chaotiques sans aucune période.

Le diagramme de branchement vous permet de suivre le développement du système avec un changement en douceur du paramètre. Avec une valeur fixe du paramètre, le diagramme en araignée (diagramme de Lamera) permet de tracer les orbites des points.

La construction d'un diagramme en araignée vous permet d'identifier divers effets invisibles sur le diagramme de branche. Écrivons un programme:


Diagramme lamera:

Doublement de la période dans les systèmes mécaniques

Considérons une équation différentielle qui modélise les vibrations amorties libres d'un point matériel d'une masse donnée sur un ressort non linéaire, à laquelle l'amortissement est déterminé par la vitesse.

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = 0$ (6)

Dans l'équation (6), le terme kx représente la force d'un ressort linéaire appliqué à un point matériel d'une masse donnée, et le terme $$$\ beta x ^ {3}$ représente la non-linéarité réelle du ressort.

Si une force agit sur le système d'oscillations libres (6), alors le déplacement du point matériel de la masse à laquelle cette force est appliquée est décrit par l'équation différentielle de Duffing pour les oscillations forcées:

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = F_ {0} cos \ omega t$ (7)

L'équation (7) pour la plupart des paramètres qui y sont inclus est résolue numériquement. Le système mécanique du modèle mathématique selon l'équation (7) est illustré dans la figure:



Une caractéristique du système donné est qu'au lieu d'un ressort, un fil métallique flexible est utilisé, qui oscille dans un plan vertical, pour lequel la constante de crochet k est négative. Dans ce schéma, les points d'équilibre stable (a) et (c), et le point d'équilibre instable (b).

Lorsqu'un point matériel est déplacé de la position (b), la force qui agit sur lui est répulsive. Si la force périodique, par exemple, créée par le champ magnétique oscillant est partiellement amortie par la résistance de l'air. Ensuite, l'équation (7) est un modèle mathématique acceptable pour le déplacement horizontal x (t) d'un point de matériau avec les plages de paramètres suivantes $$$k <0, c> 0, \ beta> 0$ .

Pour étudier le comportement d'un tel système non linéaire, nous prenons $$$k = -1, m = c = \ beta = \ omega = 1$ alors l'équation différentielle (7) prend la forme:

$$$x ^ {''} + x ^ {'} - x + x ^ {3} = F_ {0} cos (t)$ , (8)

Nous écrivons un programme d'intégration numérique de l'équation (8) dans les conditions initiales $$$x (0) = 1, x ^ {'} (0) = 0$ sur le terrain $$ et pour chacune des valeurs d'amplitude suivantes $$$F_ {0} = 0,6; 0,7; 0,75; 0,8$ , et dans chaque cas, tracez les solutions pour les avions $$$x (t), x ^ {'} (t)$ et $$$t, x (t)$ :


Graphiques résultant du programme





Cette transition du doublement de période au chaos montre le comportement général d'un système mécanique non linéaire en réponse à une modification du paramètre physique correspondant, par exemple $$$k, m, c, \ beta, \ omega, F_ {0}$ . De tels phénomènes ne se produisent pas dans les systèmes mécaniques linéaires.

Attracteur Lorenz

La substitution dans l'équation de Duffing pour les oscillations forcées (7) conduit à un système non linéaire bidimensionnel d'équations différentielles, qui a été montré dans la liste précédente. E.N.a étudié un système non linéaire tridimensionnel d'équations différentielles appliqué aux problèmes météorologiques. Lorenz:

$$$\ frac {dx} {dt} = - sx + sy,$
$$$\ frac {dy} {dt} = - xz + rx-y,$ (9)
$$$\ frac {dz} {dt} = xy-dz$

La solution du système (9) est mieux vue en projection sur l'un des trois plans. Nous écrivons un programme d'intégration numérique pour les valeurs des paramètres b = \ frac {8} {3}, s = 10, r = 28 et les conditions initiales x (0) = - 8, y (0) = 8, z (0) = 27 :


Le résultat du programme:



En considérant l'image sur le graphique au fil du temps, on peut supposer que le point P (x (t), y (t), z (t)) fait un nombre aléatoire d'oscillations, à droite ou à gauche. Pour une application météorologique du système de Lorenz, après un nombre aléatoire de jours clairs, un nombre aléatoire de jours pluvieux s'ensuit.

Considérons un programme pour cartographier l'attracteur de Lorentz dans le plan xyz pour des conditions initiales légèrement différentes:


Les résultats du programme sont présentés dans les graphiques suivants:





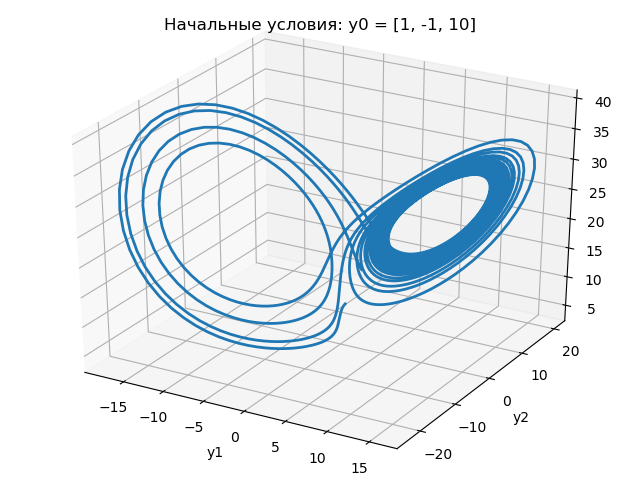
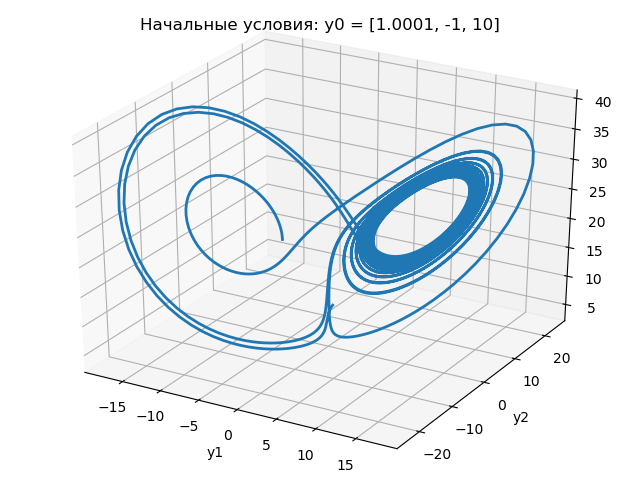
Des graphiques ci-dessus, il s'ensuit qu'un changement de la condition initiale de 1.0 à 1.0001 change radicalement la nature du changement de l'attracteur de Lorentz.

Système Rossler

Il s'agit d'un système tridimensionnel non linéaire très étudié:
$$$\ frac {dx} {dt} = - y-z,$
$$$\ frac {dy} {dt} = x- \ alpha y,$ (10)
$$$\ frac {dz} {dt} = b + x (x-c).$

Nous écrirons un programme d'intégration numérique du système (10) pour les paramètres suivants a = 0,39, b = 2, c = 4 dans les conditions initiales x (0) = 0, y (0) = 0, z (0) = 0 :


Le résultat du programme:



Dans l'avion, la bande de Rossler ressemble à une boucle, mais dans l'espace, elle se révèle tordue comme une bande de Moebius.

Conclusions

Pour démontrer les phénomènes du chaos, des programmes simples et intuitifs dans un langage de programmation Python de haut niveau sont présentés, qui sont faciles à mettre à niveau vers de nouveaux projets sur ce sujet. L'article a un objectif pédagogique et méthodologique et peut être utilisé dans le processus d'apprentissage.

Les références

1. Un peu de chaos et comment le créer
2. Un regard critique sur l'attracteur de Lorenz
3. Générateurs de chaos FPGA
4. Équations différentielles et problèmes de valeurs limites: modélisation et calcul à l'aide de Mathematica, Maple et MATLAB. 3e édition.: Per. de l'anglais - M.: LLC «I.D. Williams, 2008. - 1104 p.: Ill. - Paral. tit. Anglais