À un moment donné, pendant le développement du jeu, j'ai été confronté à la question des performances sur les PC modernes. Notre modeleur dispose d'un ordinateur d'assemblage rouge moderne assez puissant. Mais il avait notre projet terriblement lent, chargeant un cœur de processeur.
La raison est simple - les nouveaux processeurs ont de nombreux cœurs, mais en fait ils sont moins efficaces dans les applications à un seul thread. À cette époque, j'avais un rendu dans un flux. Mais en fait, les raisons n'étaient pas tellement là-dedans. Et dans le processus de recherche du problème, j'ai décidé de calculer le nombre de polygones présents dans la scène:
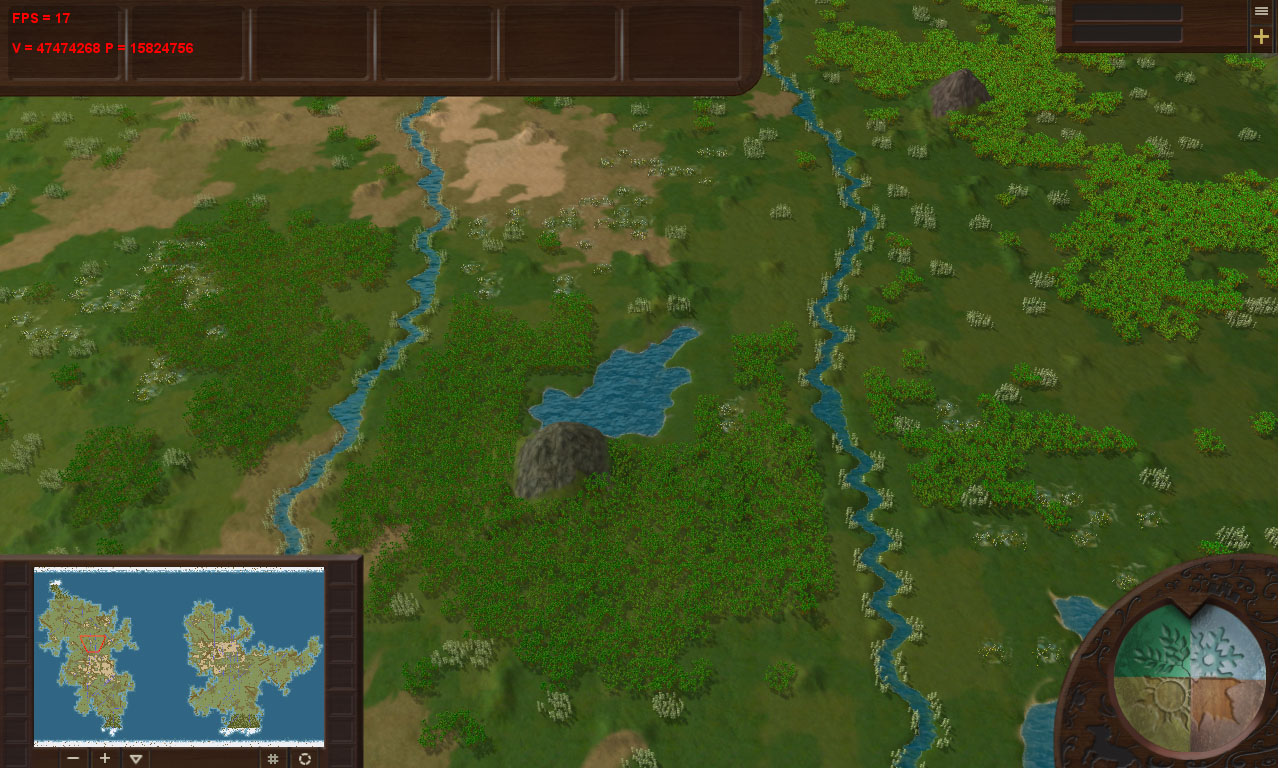
Sur la carte de jeu moyenne, avec la distance maximale et avec un grand groupe de palmiers -
15 824 756 triangles! Près de 16 millions! Un nombre énorme.
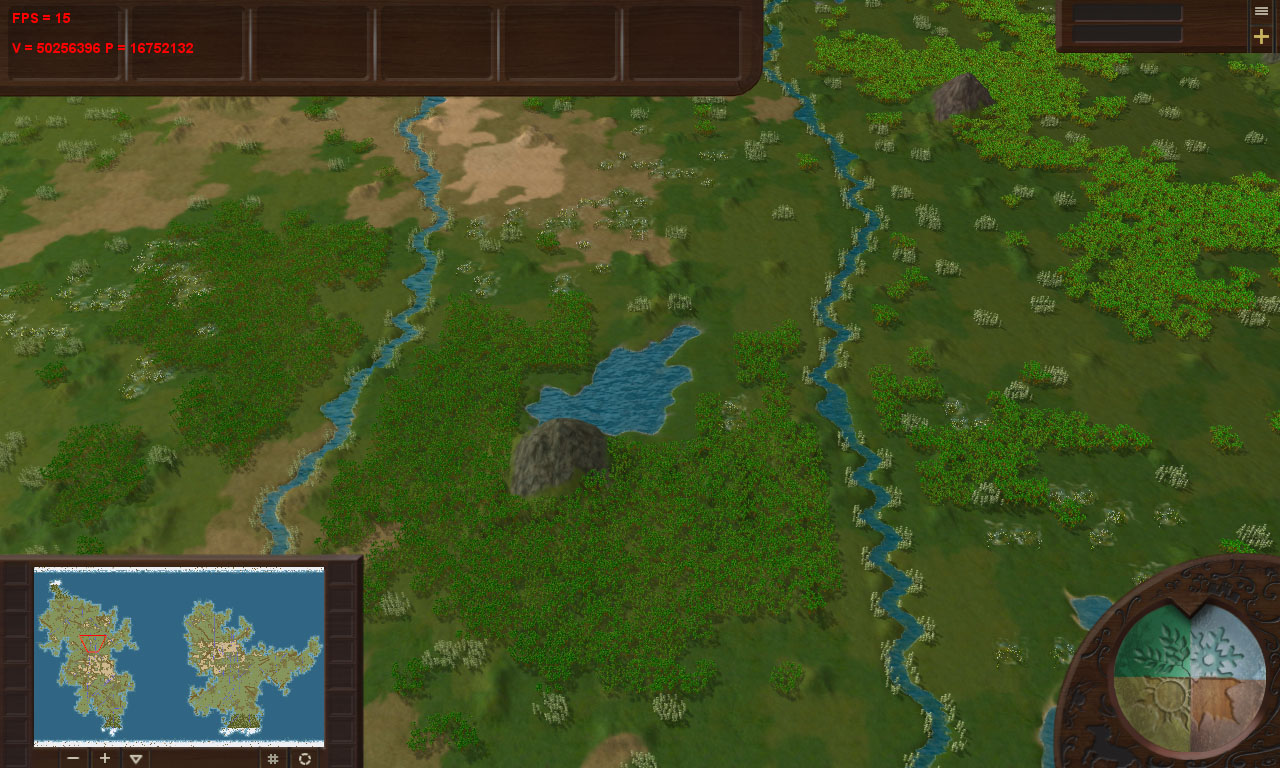
Ayant un peu joué avec le générateur de carte, j'ai réussi à trouver une place avec 16,75 millions:
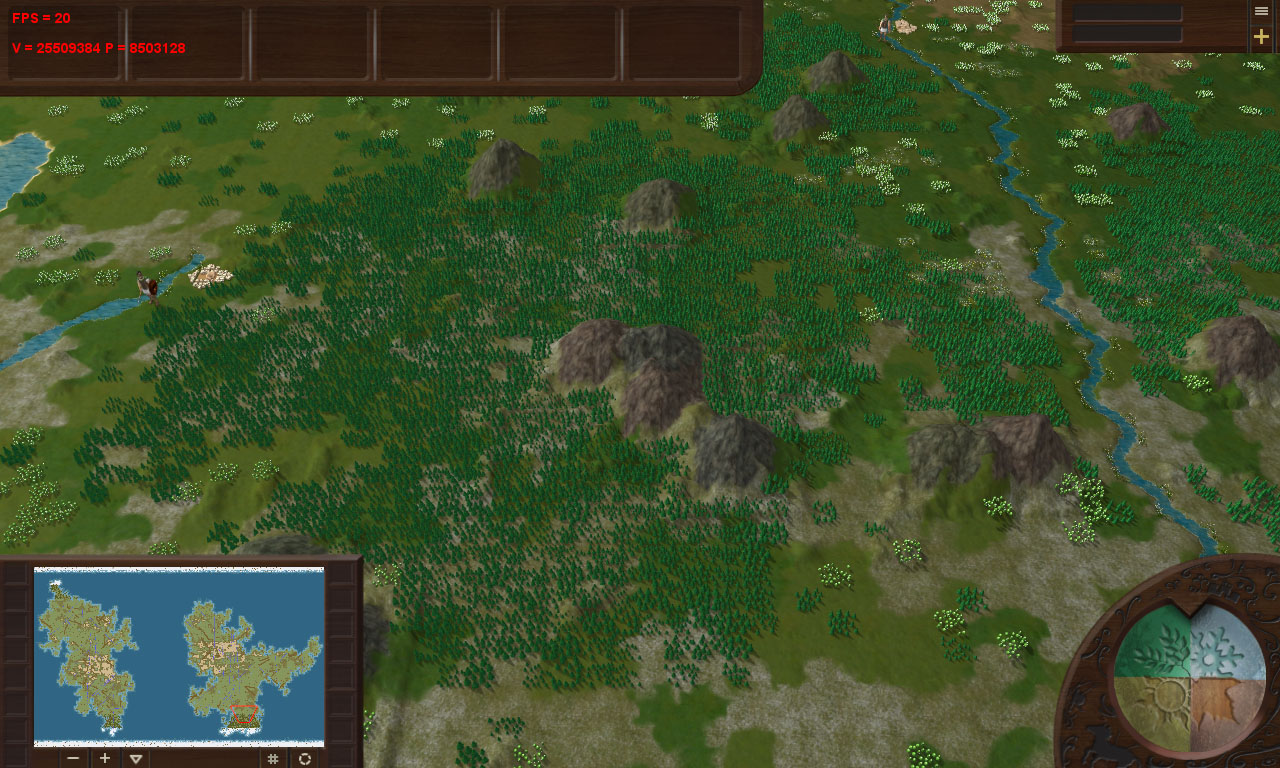
Bien que, ici, un endroit similaire avec des arbres de Noël ne donne que 8,5 millions de triangles:
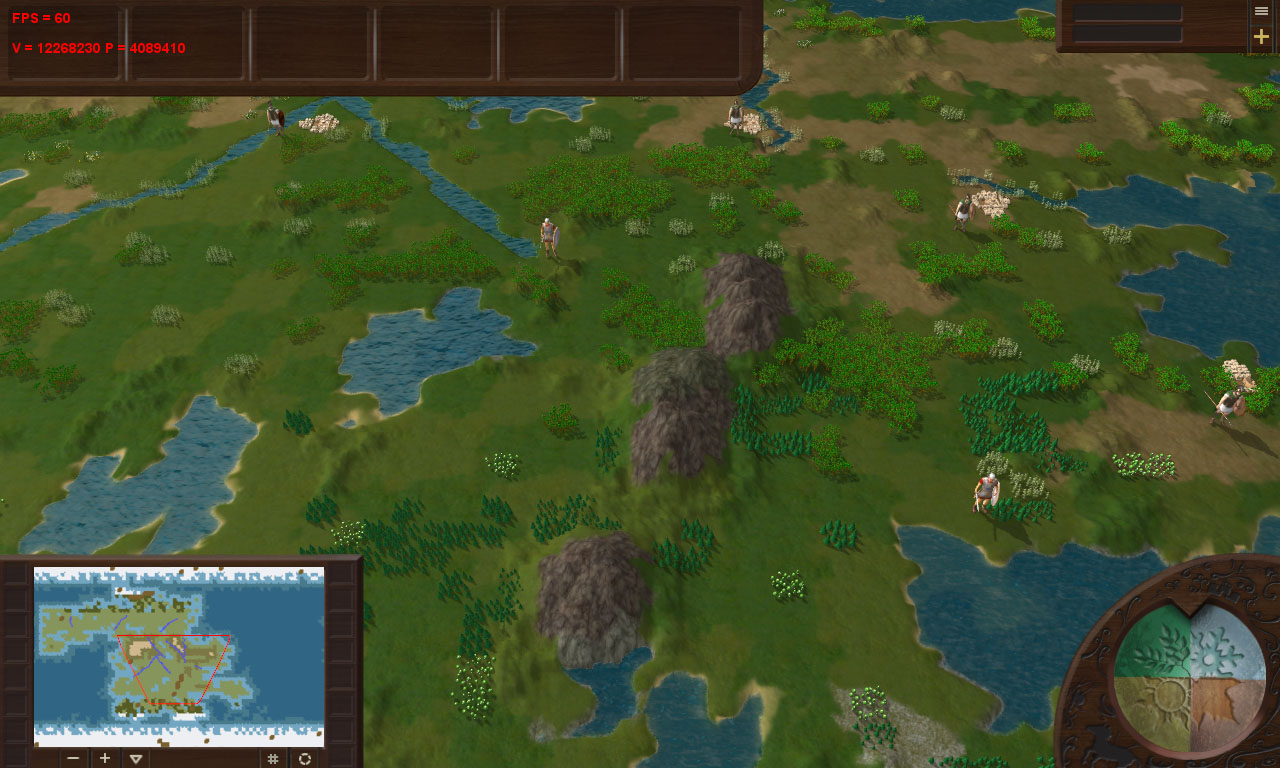
La scène moyenne se composait de ~ 4 millions:
En général, j'étais content que mon rendu fasse face à un si grand nombre de triangles, mais leur nombre était excessif. La solution était en surface:
- Optimisez le nombre de polygones dans les modèles.
- Optimisez le maillage polygonal du paysage.
- L'implémentation du rendu multi-thread.
Pour ceux qui peuvent ne pas être intéressés par le premier paragraphe de notre programme d'optimisation, par exemple les spécialistes inexpérimentés, je recommande de passer en toute sécurité à la deuxième partie.
1. Optimisation du nombre de polygones dans les modèles
Dans notre moteur, la végétation est dessinée en «packs», l'ensemble du paysage est divisé en tuiles et sous-tuiles, le pack minimum est d'une sous-tuile.

Un pack est un maillage, car la réduction du nombre de mailles réduit considérablement le nombre d'appels CPU-> GPU.

Au départ, nos arbres étaient constitués de cônes tronqués, passant à des cônes pleins, nous avons réussi à supprimer quelques triangles supplémentaires:

La cerise sur le gâteau a été la décision de retirer les troncs des arbres, car avec notre angle de caméra, ils n'étaient tout simplement pas visibles.
En conséquence, nous avons réussi à réduire le nombre de polygones, sur un paquet d'arbres de Noël, de 40% en moyenne. Les différences sont presque invisibles:

Avec les palmiers, c'était plus difficile, mais des paquets de 5000 à 6000 polygones devaient être réparés. Comment atteindre la massivité et la densité de la jungle? La haute densité de la jungle a été atteinte en raison du grand nombre de palmiers:

Nous avons décidé de simplifier les palmiers et d'introduire un deuxième niveau de végétation, ce qui nous a permis de maintenir une densité visible et d'atteindre les 600 à 700 polygones souhaités par paquet.

Réduire le nombre de polygones de 10 fois est un excellent résultat.

2. Optimisation du paysage de maillage polygonal
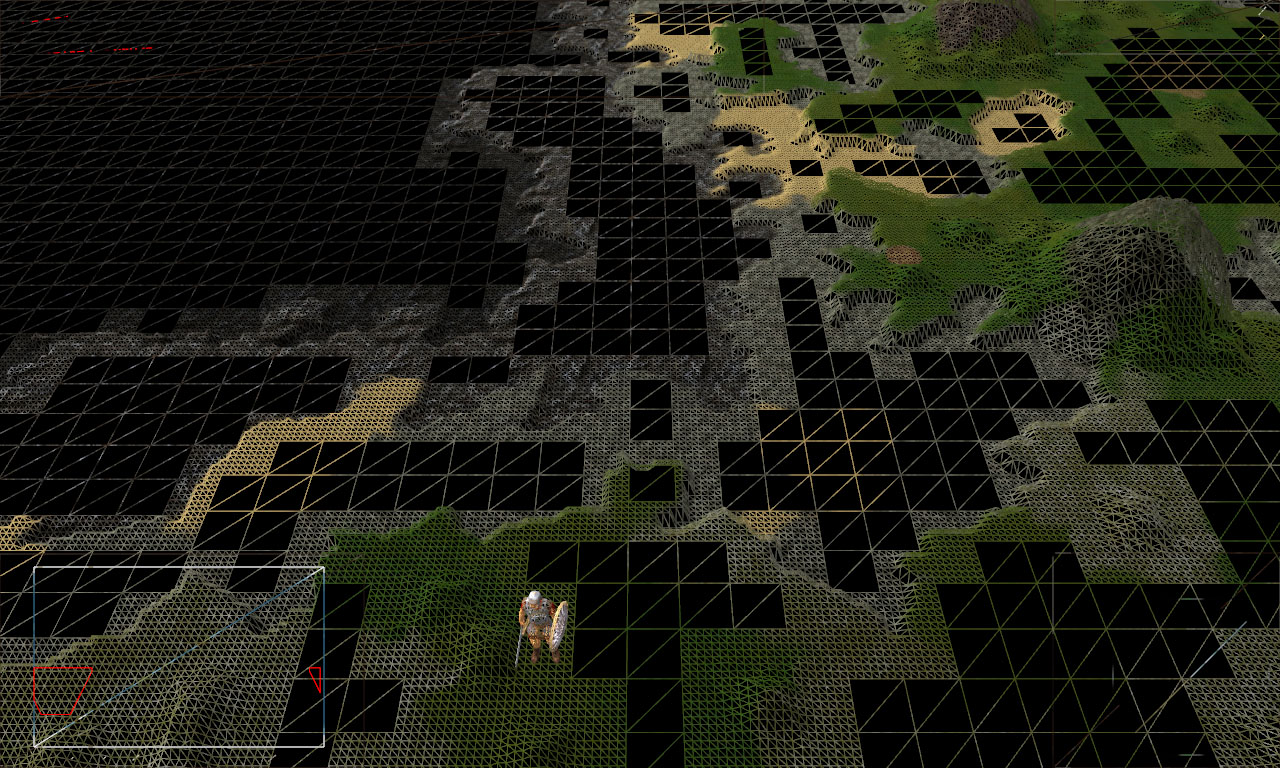
Initialement, la grille paysagère était:

La capture d'écran montre des sections simples du paysage, ce sont des carreaux de prairies, de plaines, bien que d'autres surfaces lisses. J'ai décidé de supprimer les petites irrégularités du paysage. Ainsi, il a augmenté la surface des tuiles de même hauteur. Ce n'est pas en vérifiant astucieusement tous les sommets des tuiles et sous-tuiles pour l'égalité en hauteur, j'ai réussi à obtenir ce résultat:
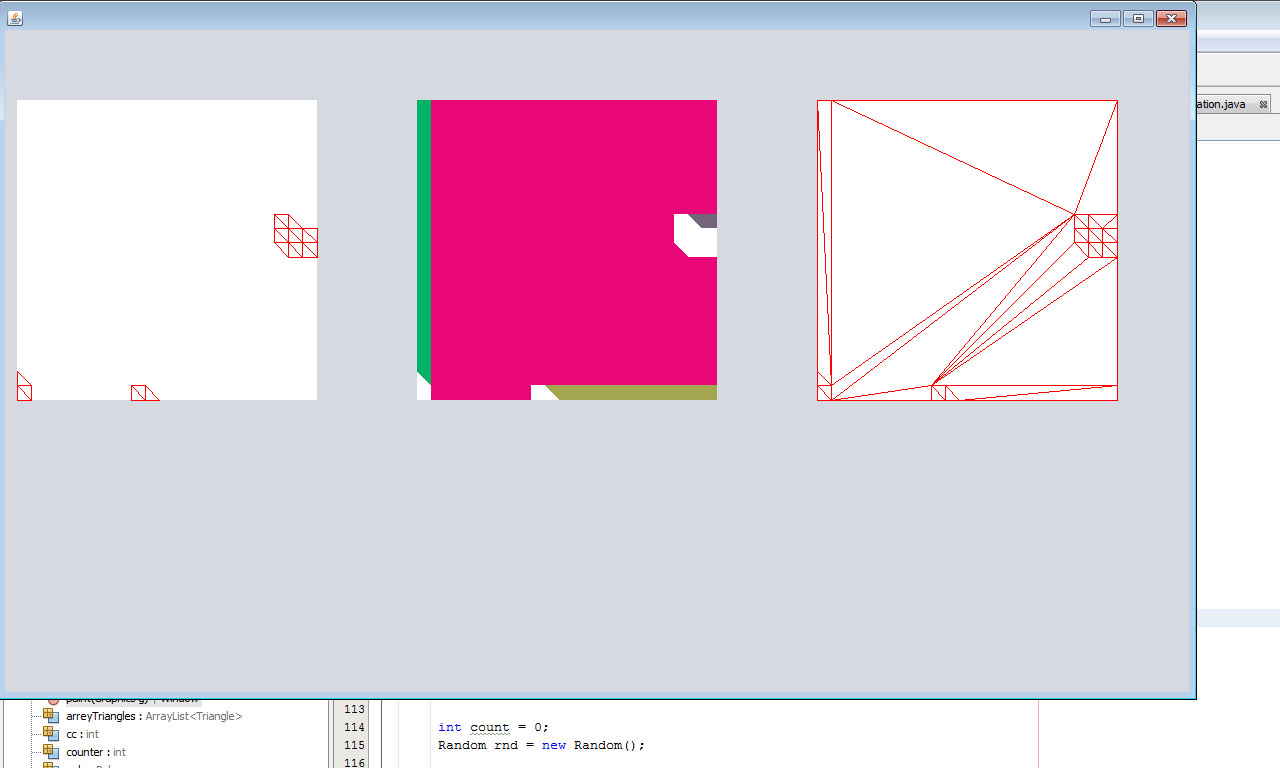
Il y avait encore des endroits plats qui pouvaient être optimisés, et j'ai commencé à construire des polygones à partir de ces triangles qui avaient la même hauteur. Une tuile a été prise et tous ses triangles ont été triés en un tableau de triangles de hauteur inégale et une liste de tableaux composés de triangles de hauteur égale et adjacents.

Dans l'exemple donné, il s'est avéré: 1 tableau de triangles qui ne peuvent pas être modifiés, car ils étaient tous de hauteurs différentes (triangles rouges) et une liste composée de deux tableaux de triangles de même hauteur (les tableaux sont remplis de couleur).
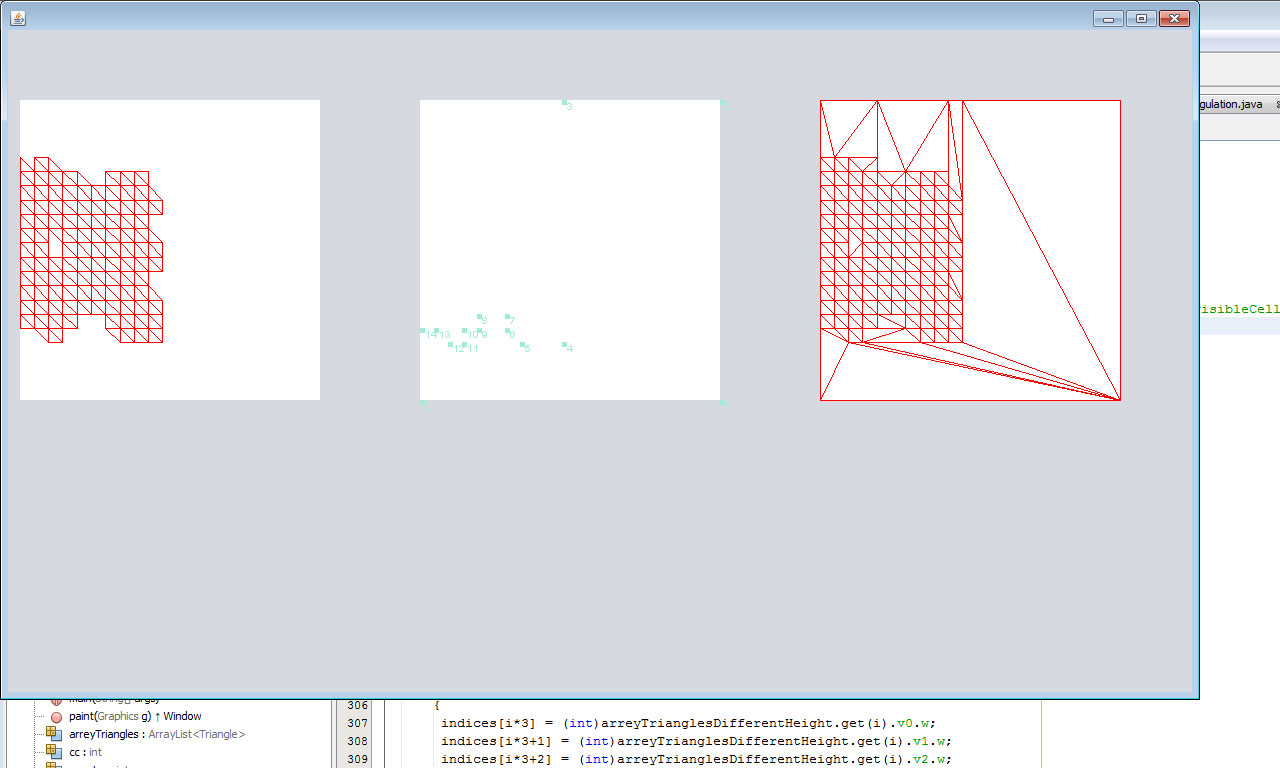
Maintenant, la tâche consistait à trouver dans le tableau de triangles leur contour convexe-concave (coque concave), et de nombreux triangles pouvaient avoir des trous. Plus tôt dans mon travail, j'ai rencontré des coques convexes, il n'y a eu aucun problème avec elles, j'ai déjà utilisé l'algorithme de Graham. Mais il y a eu des problèmes avec la construction de la coque concave ... Il s'est avéré assez difficile de trouver des informations sur ce sujet sur Internet. J'ai dû écrire une implémentation d'algorithmes à partir de zéro. Je ne mentirai pas si je dis avoir lu une dizaine de dissertations différentes sur ce sujet. Mais tous les algorithmes proposés ont donné un résultat approximatif avec quelques erreurs. Après une semaine de tourments et de douleurs, j'ai eu l'idée de mon algorithme.
J'ai essayé de construire un contour à partir de l'ensemble des sommets des triangles, c'est-à-dire J'ai traduit le tableau de triangles en un tableau de sommets et j'ai déjà construit un shell sur eux. Mais pour ma tâche, cela n'était pas nécessaire. Selon mes conclusions, la construction d'une coque directement à partir de triangles était plus facile et la précision de la coque concave était de 100%.
Au départ, je voulais mettre un patchwork du code source de l'algorithme ici, mais il semble plus facile de le décrire en quelques mots: la base est la règle: si le sommet d'un triangle est inclus dans quatre triangles ou moins, alors l'un des bords qui forme le sommet se trouve sur la frontière. Ensuite, une liste de ces bords est formée en tenant compte de la suppression des bords identiques. Nous trouvons le bord avec le plus petit X et Y et à partir de là, nous commençons le passage / tri des bords avec l'ajout de sommets uniques à la liste. Cette liste sera la coquille de nombreux triangles. La seule chose en finale est de supprimer les points colinéaires de la liste.
À la suite de cela, j'ai pu construire une coque concave de presque n'importe quelle complexité. Cet algorithme ne correspondait pas à un ensemble de trous, mais je l'ai fait en divisant simplement cet ensemble en deux moitiés dans un trou. Ensuite, j'ai eu le circuit et l'ai triangulé:
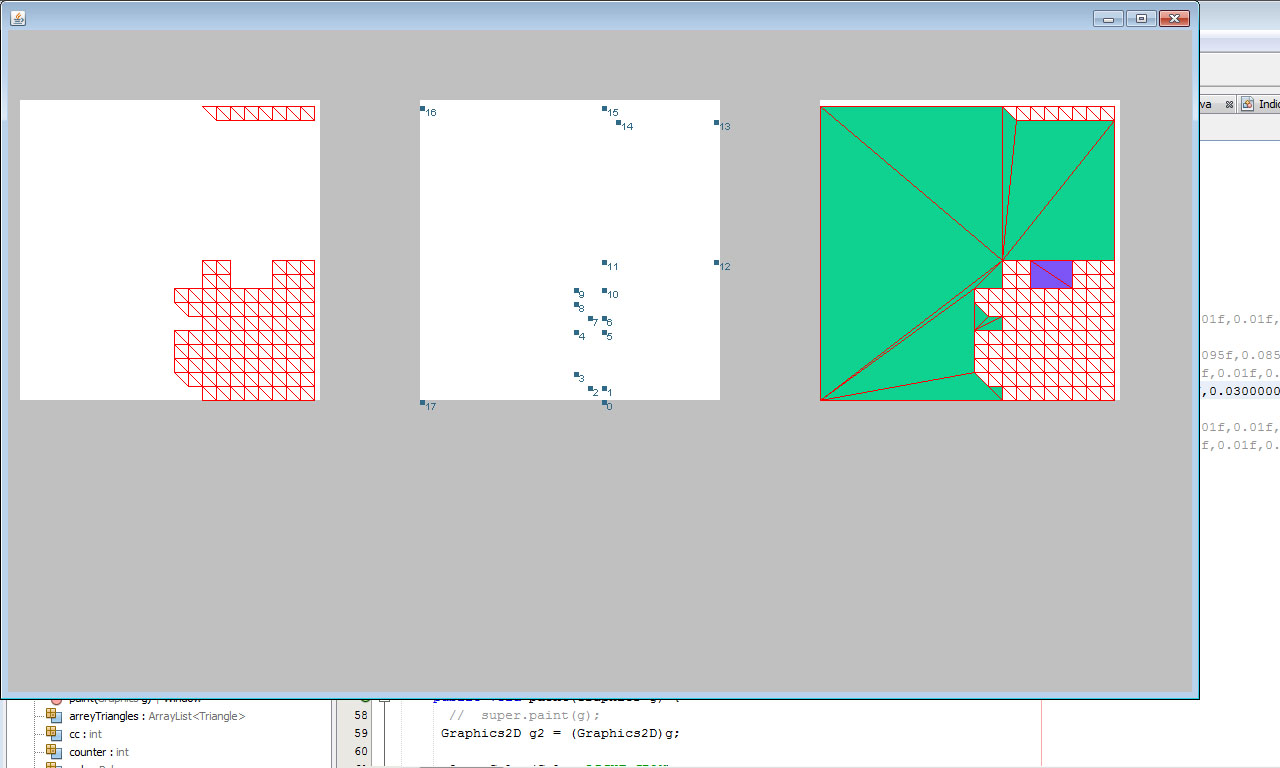
Tout s'est bien passé:

Mais au final, j'ai été bouleversé par le résultat. L'algorithme que j'ai développé a donné une augmentation tangible des performances lors du rendu d'une scène, car le nombre de polygones en moyenne a été réduit de 60 à 70%. Mais en même temps, la génération de cartes a commencé à se produire 10 fois plus lentement. L'algorithme s'est avéré être très long.
Il a fallu trois jours pour envisager une version allégée de l'algorithme d'optimisation du maillage polygonal du paysage, qui a donné ces résultats:

Maintenant, les calculs de données pour l'optimisation ne sont plus perceptibles dans le contexte de la génération de cartes, et le nombre de polygones a diminué en moyenne de 40 à 50%.
Cet article est d'essai et superficiel. Si quelqu'un s'intéresse au sujet du développement de jeux, je suis prêt à continuer et à développer l'article avec le fantôme d'étapes spécifiques, de solutions et de plans futurs. De plus, je pense que vous serez intéressé par le sujet de la construction d'une application Open GL multithread développée en Java, dont je vais essayer de parler dans le prochain article.