Récemment, du
matériel a été publié dans le magazine Quanta, dans lequel l'auteur a parlé d'un phénomène surprenant du point de vue des lecteurs inexpérimentés, prouvé par les mathématiciens. Son essence est que presque tous les polynômes d'un certain type sont irréductibles, c'est-à-dire qu'ils ne peuvent pas être décomposés. Cette preuve est appliquée dans de nombreux domaines des mathématiques pures. Mais c'est aussi une bonne nouvelle pour l'un des piliers de la vie moderne - le cryptage numérique.
Pour un stockage fiable des informations numériques, le cryptage utilisant l'algorithme RSA est largement utilisé. Il s'agit d'une version accélérée du programme que même un élève de septième année peut trouver pour échanger des messages avec des amis: chaque lettre se voit attribuer un numéro, qui est multiplié par une clé secrète et convenue à l'avance. Pour décrypter un message, il suffit de le diviser en une clé secrète.
Le cryptage RSA fonctionne de manière similaire. Nous donnons une explication très simplifiée. L'utilisateur propose un message et effectue certaines opérations mathématiques sur celui-ci, y compris la multiplication par un très grand nombre (plusieurs centaines de chiffres). La seule façon de décrypter le message est de trouver des facteurs simples du résultat *.
*Les facteurs premiers d'un nombre sont les nombres premiers qui doivent être multipliés pour obtenir ce nombre. Donc, pour le nombre 12, c'est 2 * 2 * 3, et pour le nombre 495, c'est 3, 3, 5 et 11.
La sécurité du cryptage RSA repose sur le fait que les mathématiques ne connaissent pas de moyens rapides pour trouver des facteurs premiers de très grands nombres. Et si le message chiffré ne vous était pas destiné et que vous n'avez pas de clé pour le déchiffrer, les tentatives pour trouver cette clé peuvent prendre un bon millier d'années. De plus, cela est également vrai pour les ordinateurs les plus modernes, à l'aide desquels il ne sera toujours pas possible de sélectionner les bons facteurs simples.
Mais il existe une solution de contournement.
Chaque nombre peut être représenté comme une équation algébrique unique. Et, contrairement à la recherche des facteurs premiers d'un nombre, la recherche des facteurs premiers d'un polynôme est beaucoup plus facile. Et dès que le polynôme est décomposé en de tels facteurs premiers, cette information peut être utilisée pour rechercher des facteurs premiers du nombre d'origine.
Voici comment cela fonctionne.
Première étape: choisissez n'importe quel nombre dont vous devez connaître les principaux facteurs. Pour plus de simplicité, prenez le chiffre 15.
Deuxième étape: 15 se traduit en binaire:
1111.
Troisième étape: cette expression binaire se transforme en polynôme en traduisant tous les nombres binaires en coefficients du polynôme:
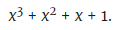
(Remarque: ce polynôme est 15 si x = 2. Le numéro 2 est la base du système binaire.)
Quatrième étape: Le polynôme est factorisé:
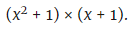Cinquième étape: x = 2 est substitué dans chacun de ces facteurs:
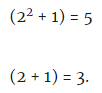Conclusion: 5 et 3 sont des facteurs premiers de 15.
Oui, c'est une façon trop compliquée de trouver des facteurs simples d'un petit nombre comme 15, qui sont faciles à comprendre dans l'esprit. Cependant, lorsqu'il s'agit de grands nombres composés de centaines de nombres, cette méthode polynomiale offre un avantage incroyable. Pour décomposer les nombres premiers, les algorithmes rapides n'existent pas. Mais il existe de tels algorithmes pour décomposer de grands polynômes. Par conséquent, dès que vous parvenez à transformer un grand nombre en un grand polynôme, vous pouvez être très près de trouver des facteurs simples du nombre.
Est-ce à dire que le cryptage RSA est en danger? Pas vraiment. Et un nouveau modèle récemment prouvé concernant les polynômes est précisément lié à cela.
Les mathématiciens
Emmanuel Brulya et
Peter Varju de l'Université de Cambridge ont prouvé que plus les polynômes avec les coefficients 0 et 1 s'allongent, plus la probabilité qu'ils puissent être étendus diminue. Et si le polynôme ne peut pas être décomposé, il ne peut pas être utilisé pour rechercher des facteurs simples du nombre à calculer.
Les preuves de Brull et Varju suggèrent en fait qu'une solution de contournement pour casser le chiffrement RSA ne mène nulle part. Les très grands nombres utilisés dans RSA correspondent à des polynômes très longs. Les scientifiques de Cambridge affirment qu'il est presque impossible de trouver des polynômes de cette longueur qui peuvent être décomposés. Les cryptographes et les mathématiciens soupçonnent depuis longtemps qu'il en est ainsi. Cependant, lorsque la cybersécurité mondiale dépend de l'impossibilité d'utiliser une technique mathématique, il est toujours bon d'avoir la preuve que cette technique ne fonctionne pas vraiment.
