Biquaternions

Si vous avez ouvert cet article, vous avez probablement déjà entendu parler des quaternions, et peut-être même les utilisez-vous dans vos créations. Mais il est temps de s'élever à un niveau supérieur - jusqu'aux biquaternions.

Cet article donne des concepts de base sur les biquaternions et les opérations avec eux. Pour une meilleure compréhension de l'utilisation des biquaternions, un exemple clair en Javascript utilisant Canvas est montré.

Biquaternion

Le biquaternion est un nombre hypercomplexe ayant une dimension de 8. Dans les articles et la littérature de langue anglaise, ils sont appelés «dual quaternion», et dans la littérature de langue russe, il existe également les noms de «dual quaternion» ou «complex quaternion».

La principale différence avec les quaternions est que le quaternion décrit l'orientation de l'objet dans l'espace, et le biquaternion décrit également la position de l'objet dans l'espace.

Le biquaternion peut être représenté par deux quaternions:

$$

$$\ widetilde {\ textbf {q}} = \ begin {bmatrix} \ textbf {q} _1 \\ \ textbf {q} _2 \ end {bmatrix},$$

$$$\ textbf {q} _1$ - la partie réelle, détermine l'orientation de l'objet dans l'espace;
$$$\ textbf {q} _2$ - la partie double, détermine la position de l'objet dans l'espace.

Le biquaternion est également appelé le quaternion complexe, dans ce cas, il est représenté comme un quaternion, dont chaque composant est un nombre double (à ne pas confondre avec le complexe). Numéro double $$$A = a_1 + \ epsilon a_2$ où $$$a_1$ et $$$a_2$ Sont des nombres réels, et $$$\ epsilon$ - Symbole Clifford (complexité), possédant la propriété $$$\ epsilon ^ 2 = 0$ . Nous ne nous attarderons pas sur les mathématiques, car nous nous intéressons davantage à la partie appliquée, par conséquent, nous considérerons le biquaternion comme deux quaternions.

Interprétation géométrique du biquaternion

Par analogie avec le quaternion, avec lequel vous pouvez définir l'orientation de l'objet, le biquaternion peut également définir la position. C'est-à-dire Le biquaternion définit deux valeurs à la fois - la position et l'orientation de l'objet dans l'espace. Si nous les considérons dans la dynamique, alors le biquaternion définit deux quantités - la vitesse linéaire de mouvement et la vitesse angulaire de rotation de l'objet. La figure ci-dessous montre la signification géométrique du biquaternion.



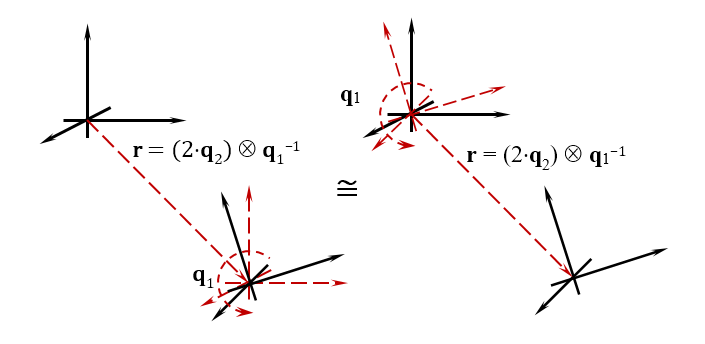
Les développeurs de jeux savent que pour déterminer la position et l'orientation d'un objet dans l'espace de jeu, des matrices de rotation et des matrices de déplacement sont utilisées et, selon l'ordre dans lequel vous les appliquez, le résultat de la position finale de l'objet est différent. Pour ceux qui sont habitués à diviser le mouvement en opérations distinctes, acceptez la règle pour travailler avec des biquaternions: d'abord nous déplaçons l'objet, puis nous le faisons pivoter. En fait, vous décrivez ces deux mouvements avec un seul numéro, bien qu'il s'agisse d'un hypercomplexe complexe.

Caractéristiques scalaires

Considérez les principales caractéristiques scalaires. Ici, il faut faire attention au fait qu'ils ne renvoient pas des nombres réels ordinaires, mais des nombres doubles.

1. La norme du biquaternion

$$

$$\ | \ widetilde {\ textbf {q}} \ | = \ | \ textbf {q} _1 \ | + \ epsilon (q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2)$$

2. Module Biquaternion

$$

$$| \ widetilde {\ textbf {q}} | = | \ textbf {q} _1 | + \ epsilon \ frac {q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2} {| \ textbf {q} _1 |}$$

Opérations de base

Considérez les opérations de base de l'utilisation des biquaternions. Comme vous pouvez le voir, ils sont très similaires à des opérations similaires avec des quaternions.

1. Jumelage biquaternion

$$

$$\ widetilde {\ textbf {q}} ^ * = \ begin {bmatrix} \ textbf {q} _1 ^ * \\ \ textbf {q} _2 ^ * \ end {bmatrix}$$

2. Addition et soustraction de biquaternions

$$

$$\ widetilde {\ textbf {q}} \ pm \ widetilde {\ textbf {p}} = \ begin {bmatrix} \ textbf {q} _1 \ pm \ textbf {p} _1 \\ \ textbf {q} _2 \ pm \ textbf {p} _2 \ end {bmatrix}$$

L'addition et la soustraction de biquaternions sont commutatives (les termes peuvent être échangés).

3. Multiplication du nombre réel par biquaternion

$$

$$a \ widetilde {\ textbf {q}} = \ widetilde {\ textbf {q}} a = \ begin {bmatrix} a \ textbf {q} _1 \\ a \ textbf {q} _2 \ end {bmatrix}$$

4. Multiplication du biquaternion

$$

$$\ widetilde {\ textbf {q}} \ otimes \ widetilde {\ textbf {p}} = \ begin {bmatrix} \ textbf {q} _1 \ otimes \ textbf {p} _1 \\ \ textbf {q} _1 \ otimes \ textbf {p} _2 + \ textbf {q} _2 \ otimes \ textbf {p} _1 \ end {bmatrix}$$

La multiplication des biquaternions n'est pas commutative (avec un changement dans l'ordre des facteurs, le résultat de la multiplication des biquaternions est différent).

Cette opération est l'une des principales lorsque vous travaillez avec des biquaternions et a une signification physique, à savoir que le résultat de la multiplication des biquaternions est l'opération consistant à ajouter les rotations et les mouvements linéaires de deux biquaternions.

5. Biquaternion inversé

$$

$$\ widetilde {\ textbf {q}} ^ {- 1} = \ frac {\ widetilde {\ textbf {q}} ^ *} {\ | \ widetilde {\ textbf {q}} \ |}$$

Détermination du biquaternion par les angles d'orientation et le vecteur de position

Tout d'abord, nous définissons les systèmes de coordonnées dans lesquels nous considérerons l'orientation et la position de l'objet dans l'espace. Cela doit être fait pour spécifier la partie réelle du biquaternion (quaternion d'orientation), dont la séquence de rotation affecte le quaternion résultant à partir des angles d'orientation. Ici, nous serons guidés par les angles de l'avion - lacet $$$\ psi$ pas $$$\ vartheta$ et rouler $$$\ gamma$ .

Définissez le système de coordonnées de base. Imaginez que vous vous tenez à la surface de la Terre et que vous regardez en direction du Nord.

Point O _o - l'origine du système de coordonnées, situé au point d'origine de l'objet.
L'axe O _o Y _g - est dirigé verticalement vers le haut et est opposé à la direction du vecteur de gravité.
L'axe O _o X _g - est dirigé vers le nord, le long de la tangente du méridien local.
L'axe O _o Z _g - complète le système vers la droite et est dirigé vers la droite, vers l'est.

Le deuxième système de coordonnées est connecté. Imaginez, par exemple, un avion ou un autre objet.
Point O - l'origine du système de coordonnées, en règle générale, est située au centre de masse de l'objet.
Axe OY - dirigé verticalement vers le haut et perpendiculaire au plan horizontal de l'objet.
Axis OX - dirigé vers l'avant jusqu'au point avant de l'objet.
Axe OZ - complète le système vers la droite.

La position de l'objet dans l'espace est déterminée par le vecteur rayon de l'origine (point O ) du système de coordonnées associé par rapport au système de coordonnées de base fixe. L'orientation du système de coordonnées associé par rapport à la base est déterminée par trois allumages successifs:

angle de lacet $$$\ psi$ - rotation autour de l'axe OY ,
angle de tangage $$$\ vartheta$ - rotation autour de l'axe OZ ,
angle de roulis $$$\ gamma$ - rotation autour de l'axe OX .

Pour la détermination initiale du biquaternion, vous devez spécifier les parties réelle et double du biquaternion. L'orientation et la position de l'objet sont définies par rapport à un certain système de coordonnées de base en utilisant des angles d'orientation $$$\ psi, \ vartheta, \ gamma$ et vecteur de position du centre de masse $$$r = (r_x, r_y, r_z) ^ T$ .

La vraie partie $$$\ textbf {q} _1$ peut être défini à l'aide de la formule:

$$

$$\ textbf {q} _1 = \ begin {bmatrix} \ cos \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} & - & \ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ cos \ frac { \ vartheta} {2} \ sin \ frac {\ gamma} {2} & + & \ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} & + & \ sin \ frac {\ psi} { 2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} & - & \ sin \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \ end {bmatrix}$$

Veuillez noter que si vous avez une séquence de rotation différente, les expressions seront également différentes.

Double partie $$$\ textbf {q} _2$ défini par l'expression:

$$

$$\ textbf {q} _2 = \ frac12 \ textbf {r} \ otimes \ textbf {q} _1$$

Calcul des angles d'orientation et du vecteur de position à partir du biquaternion. Transformation inverse

Les angles d'orientation peuvent être calculés à partir de la partie réelle du biquaternion $$$\ textbf {q} _1$ :

$$

$$\ psi = \ arctan {\ frac {2 (q_0 q_2 - q_1 q_3)} {q_0 ^ 2 + q_1 ^ 2 - q_2 ^ 2 - q_3 ^ 2}}$$

$$

$$\ vartheta = \ arcsin {(2 (q_1 q_2 + q_0 q_3))}$$

$$

$$\ gamma = \ arctan {\ frac {2 (q_0 q_1 - q_2 q_3)} {q_0 ^ 2 - q_1 ^ 2 + q_2 ^ 2 - q_3 ^ 2}}$$

La position de l'objet est déterminée par l'expression:

$$

$$\ textbf {r} = 2 \ textbf {q} _2 \ otimes \ textbf {q} _1 ^ {- 1}$$

le résultat est un vecteur sous forme de quaternion $$$\ textbf {r} = (0, r_x, r_y, r_z) ^ T$

Faire pivoter et déplacer le vecteur biquaternion

L'une des grandes propriétés des biquaternions est la rotation et le mouvement d'un vecteur d'un système de coordonnées à un autre. Soit O _o X _g Y _g Z _g un système de coordonnées de base fixe, et OXYZ le système de coordonnées connecté de l'objet. Ensuite, l'orientation et la position de l'objet par rapport au système de coordonnées de base peuvent être spécifiées par le biquaternion $$$\ widetilde {\ textbf {q}}$ . Si un vecteur est spécifié $$$\ textbf {r}$ dans un système de coordonnées connecté, vous pouvez obtenir un vecteur $$$\ textbf {r} _0$ dans le système de coordonnées de base en utilisant la formule:

$$

$$\ textbf {r} _0 = \ widetilde {\ textbf {q}} \ otimes \ textbf {r} \ otimes \ widetilde {\ textbf {q}} ^ {- 1}$$

et retour:

$$

$$\ textbf {r} = \ widetilde {\ textbf {q}} ^ {- 1} \ otimes \ textbf {r} _0 \ otimes \ widetilde {\ textbf {q}}$$

où $$$\ textbf {r}$ Est un vecteur sous forme de biquaternion, $$$\ textbf {r} = (1, 0, 0, 0, 0, 0, r_x, r_y, r_z)$

Bibliothèque JavaScript Biquaternion

Toutes les opérations ci-dessus avec biquaternions sont implémentées dans la bibliothèque javascript, en fonction de vos tâches, elles peuvent être implémentées dans d'autres langages de programmation. Les principales fonctions du travail avec les biquaternions:

Fonction	La description
DualQuaternion.dq	Corps biquaternion sous forme de tableau de 8 nombres
DualQuaternion(dq0, dq1, dq2, dq3, dq4, dq5, dq6, dq7)	Un constructeur qui définit un biquaternion en spécifiant les huit nombres
DualQuaternion.fromEulerVector(psi, theta, gamma, v)	Obtenez le biquaternion en définissant l'orientation de l'objet avec des angles d'Euler et le vecteur de position de l'objet
DualQuaternion.getEulerVector()	Obtenez les angles d'Euler et le vecteur de position à partir du biquaternion
DualQuaternion.getVector()	Obtenez le vecteur de position de biquaternion
DualQuaternion.getReal()	Obtenez la partie réelle du biquaternion (détermine l'orientation de l'objet dans l'espace)
DualQuaternion.getDual()	Obtenez la double partie du biquaternion (détermine la position de l'objet dans l'espace)
DualQuaternion.norm()	Obtenez la norme biquaternion sous la forme d'un nombre double
DualQuaternion.mod()	Obtenez le module biquaternion en tant que numéro double
DualQuaternion.conjugate()	Obtenez le biquaternion conjugué
DualQuaternion.inverse()	Obtenez Biquaternion inversé
DualQuaternion.mul(DQ2)	Multiplication de biquaternions
DualQuaternion.toString()	Convertir biquaternion en chaîne, par exemple, pour la sortie vers la console de débogage

Un exemple de travail avec des biquaternions

Pour une meilleure compréhension des bases de l'utilisation des biquaternions comme exemple, considérons un petit jeu. La zone rectangulaire est définie - la carte. Un navire flottant sur une carte avec un pistolet rotatif monté sur la carte. Ici, il faut tenir compte du fait que pour le navire, le système de coordonnées de base est le système de coordonnées de la carte, et pour le canon, le système de coordonnées de base est le navire. Tous les objets sont dessinés dans le système de coordonnées de la carte et ici, il sera intéressant de voir comment vous pouvez passer du système de coordonnées du pistolet au système de coordonnées de la carte en utilisant la propriété de multiplication biquaternion. Le mouvement du navire est contrôlé par les touches W, A, S, D. La direction du pistolet est définie par le curseur de la souris.



Le navire et le canon sont décrits par deux classes: le navire et le canon. Dans le constructeur de la classe de navire, sa forme sous la forme de points de biquaternion, l'orientation et la position initiales sur la carte sous la forme de this.dq_pos biquaternion de this.dq_pos sont this.dq_pos .

Des incréments de biquaternion sont également donnés pour le contrôle des navires. Lorsque vous vous déplacez d'avant en arrière (touches W, S), seule la partie double du biquaternion change et lorsque vous contrôlez de droite à gauche (touches A, D), la partie réelle et double du biquaternion change, ce qui définit l'angle de rotation.

 function Ship(ctx, v) { this.ctx = ctx; this.dq_pos = new DualQuaternion.fromEulerVector(0*Math.PI/180, 0, 0, v); //   this.dq_forward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, -10]); this.dq_forward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, 10]); this.dq_backward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, -10]); this.dq_backward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, 10]); this.dq_forward_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 30, 0, 0]); //      this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 1, 0, 0]); this.dq_dx_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [-1, 0, 0]); return this; }; 

Dans la classe elle-même, il n'y a qu'une seule fonction pour rendre le Ship.draw() . Faites attention à l'application de l'opération biquaternion consistant à multiplier chaque point du navire par le biquaternion de la position et de l'orientation actuelles du navire.

 Ship.prototype = { 'ctx': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, 0, 0, 0), /** *   */ 'draw': function() { //         v_pos = this.dq_pos.getVector(); v_forward_left = this.dq_pos.mul(this.dq_forward_left).getVector(); v_forward_right = this.dq_pos.mul(this.dq_forward_right).getVector(); v_backward_left = this.dq_pos.mul(this.dq_backward_left).getVector(); v_backward_right = this.dq_pos.mul(this.dq_backward_right).getVector(); v_forward_forward = this.dq_pos.mul(this.dq_forward_forward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward_left[0], v_backward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_forward[0], v_forward_forward[2]); ctx.lineTo(v_forward_right[0], v_forward_right[2]); ctx.lineTo(v_backward_right[0], v_backward_right[2]); ctx.lineTo(v_backward_left[0], v_backward_left[2]); ctx.stroke(); ctx.closePath(); } }; 

Dans le constructeur de la classe des armes à feu, sa forme sous la forme de points biquaternion est spécifiée. Le pistolet sera affiché sous forme de ligne. L'orientation et la position initiales sur le navire sont définies par le biquaternion this.dq_pos . En outre, la liaison avec le navire sur lequel il est installé est également définie. Le pistolet sur le navire ne peut que tourner, donc les incréments de biquaternion lors du contrôle du pistolet ne changeront que la partie réelle du biquaternion, qui définit l'angle de rotation. Dans cet exemple, l'outil est guidé par le curseur de la souris, de sorte que la rotation du pistolet se produira instantanément.

 function Gun(ctx, ship, v) { this.ctx = ctx; this.ship = ship; //     this.dq_pos = new DualQuaternion.fromEulerVector(0, 0, 0, v); //   this.dq_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [20, 0, 0]); this.dq_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 0, 0, 0]); //     this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); return this; }; 

Dans la classe gun, une seule fonction de son rendu Ship.draw() également implémentée. Le pistolet est affiché sous la forme d'une ligne définie par deux points this.dq_backward et this.dq_forward . Pour déterminer les coordonnées des points de canon, l'opération de multiplication biquaternion est utilisée.

 Gun.prototype = { 'ctx': 0, 'ship': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]), /** *   */ 'draw': function() { //     v_pos = this.ship.dq_pos.getVector(); v_forward = this.ship.dq_pos.mul(this.dq_backward).mul(this.dq_forward).getVector(); v_backward = this.ship.dq_pos.mul(this.dq_backward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward[0], v_backward[2]); ctx.lineTo(v_forward[0], v_forward[2]); ctx.stroke(); ctx.closePath(); } }; 

Le traitement du contrôle des navires et des armes à feu est mis en œuvre au moyen d'événements. Quatre variables leftPressed, upPressed, rightPressed, downPressed , qui sont traitées dans la boucle de programme principale, sont chargées d'appuyer et de relâcher les touches de commande du navire.

 leftPressed = false; rightPressed = false; upPressed = false; downPressed = false; dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]); document.addEventListener("keydown", keyDownHandler, false); document.addEventListener("keyup", keyUpHandler, false); document.addEventListener("mousemove", mouseMoveHandler, false); //     function keyDownHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = true; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = true; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = true; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = true; } //  S } //     function keyUpHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = false; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = false; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = false; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = false; } //  S } 

L'une des fonctions les plus intéressantes, du point de vue de l'utilisation des opérations de biquaternion, est de contrôler le canon du navire dans la direction du pointeur de la souris. Tout d'abord, les coordonnées du pointeur de la souris sont déterminées dans le biquaternion dq_mouse_pos . Ensuite, le biquaternion de la position de la souris par rapport au navire est calculé en utilisant la multiplication du biquaternion. Le biquaternion du navire provient de la souris biquaternion dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos);
(Remarque: les opérations de multiplication biquaternion séquentielles se lisent de droite à gauche). Et enfin, l'angle entre les vecteurs de l'outil et de la souris est déterminé. Le point de départ du pistolet gun_1.dq_backward reçoit la valeur reçue.

 function mouseMoveHandler(e) { var relativeX = e.clientX - canvas.offsetLeft; var relativeY = e.clientY - canvas.offsetTop; //           if (relativeX > 0 && relativeX < canvas.width && relativeY > 0 && relativeY < canvas.height) { //    dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [relativeX, 0, relativeY]); //      //  .       //     // DQ_ship^(-1) * DQ_mouse dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos); //       q_gun_mouse = new Quaternion.fromBetweenVectors(gun_1.dq_forward.getVector(), dq_mouse_pos_about_ship.getVector()); dq_gun_mouse = new DualQuaternion(q_gun_mouse.q[0], q_gun_mouse.q[1], q_gun_mouse.q[2], q_gun_mouse.q[3], 0, 0, 0, 0); gun_1.dq_backward = dq_gun_mouse; // console.log(dq_gun_mouse.getEulerVector()); // console.log(relativeX + ' ' + relativeY + ' ' + gun_1.dq_forward.toString()); } } 

Dans le corps principal du programme, les objets du navire et des canons ship_1 et gun_1 , les informations de débogage sont affichées et le traitement de contrôle du navire est effectué.

 var canvas = document.getElementById("myCanvas"); var ctx = canvas.getContext("2d"); ship_1 = new Ship(ctx, [100, 0, 100]); gun_1 = new Gun(ctx, ship_1, [0, 0, 0]); function draw() { ctx.clearRect(0, 0, canvas.width, canvas.height); ship_1.draw(); gun_1.draw(); // Debug info ship_euler_vector = ship_1.dq_pos.getEulerVector(); ship_euler_vector[0] = ship_euler_vector[0]*180/Math.PI; ship_euler_vector[1] = ship_euler_vector[1]*180/Math.PI; ship_euler_vector[2] = ship_euler_vector[2]*180/Math.PI; ship_euler_vector = ship_euler_vector.map(function(each_element){ return each_element.toFixed(2); }); ship_dq = ship_1.dq_pos.dq.map(function(each_element){ return each_element.toFixed(2); }); gun_dq = ship_1.dq_pos.mul(gun_1.dq_backward).dq.map(function(each_element){ return each_element.toFixed(2); }); ctx.font = "8pt Courier"; ctx.fillText("Ship: " + ship_dq + " | psi, theta, gamma, vector:" + ship_euler_vector, 10, 20); ctx.fillText("Gun: " + gun_dq, 10, 40); //   if (leftPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_left); } if (rightPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_right); } if (upPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_forward); } if (downPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_backward); } requestAnimationFrame(draw); } draw(); 

Le lien vers l'archive contient le code complet des bibliothèques pour travailler avec les quaternions et les biquaternions, le script du programme lui-même et le fichier index.html, qui peut être ouvert localement dans le navigateur afin d'exécuter l'exemple ci-dessus.

Un exemple de travail avec des biquaternions

Conclusion

Vous vous posez peut-être une question: pourquoi utiliser un appareil mathématique aussi complexe alors que vous pouvez vous en tirer avec des outils standard pour déplacer et faire tourner des objets? L'un des principaux avantages est que la forme d'écriture biquaternion est plus efficace en termes de calcul, car toutes les opérations avec des biquaternions après le développement des expressions sont linéaires. Cette vidéo, Skinning géométrique avec mélange approximatif de quaternions doubles, montre à quel point les calculs de biquaternions sont plus efficaces que les autres méthodes.

J'ai principalement pris des informations sur l'utilisation des biquaternions de sources anglaises.
De la littérature domestique, je peux conseiller deux livres:

1. Chelnokov Yuri Nikolaevich. Modèles quaternion et biquaternion et méthodes de la mécanique des solides et leurs applications. Géométrie et cinématique du mouvement. - travail théorique monumental.
2. Gordeev Vadim Nikolaevich. Quaternions et biquaternions avec des applications en géométrie et en mécanique. - Il est écrit dans un langage plus compréhensible et montre des applications dans les tâches de mise en forme de structures spatiales courbes.