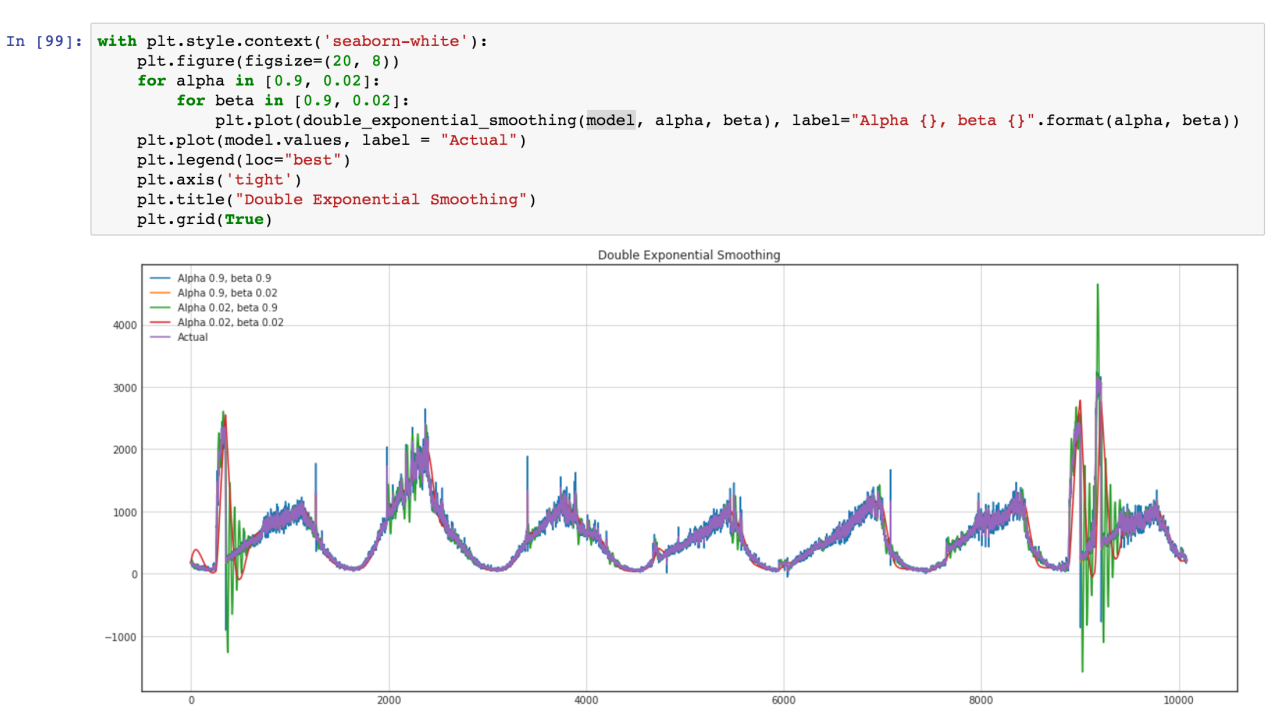
Il s'agit d'un court article sur la compréhension des séries chronologiques et des principales caractéristiques qui en découlent.
Énoncé du problème
Nous avons des données chronologiques avec une régularité quotidienne et hebdomadaire. Nous voulons découvrir comment modéliser ces données de manière optimale.

Analyser les séries chronologiques
L'une des caractéristiques importantes des séries chronologiques est la stationnarité.
En mathématiques et statistiques, un processus stationnaire (alias un processus stationnaire strict (ly) ou un processus stationnaire fort (ly)) est un processus stochastique dont la distribution de probabilité conjointe ne change pas lorsqu'il est décalé dans le temps.
Par conséquent, des paramètres tels que la moyenne et la variance, s'ils sont présents, ne changent pas non plus avec le temps. Étant donné que la stationnarité est une hypothèse sous-jacente à de nombreuses procédures statistiques utilisées dans l'analyse des séries chronologiques, les données non stationnaires sont souvent transformées pour devenir stationnaires.
Les causes les plus fréquentes de violation de la stationnarité sont les tendances de la moyenne, qui peuvent être dues soit à la présence d'une racine unitaire, soit à une tendance déterministe. Dans le premier cas d'une racine unitaire, les chocs stochastiques ont des effets permanents et le processus ne revient pas à la moyenne. Dans le dernier cas d'une tendance déterministe, le processus est appelé processus stationnaire de tendance, et les chocs stochastiques n'ont que des effets transitoires qui reviennent à la moyenne (c'est-à-dire que la moyenne revient à sa moyenne à long terme, qui change déterministe au fil du temps selon la tendance).
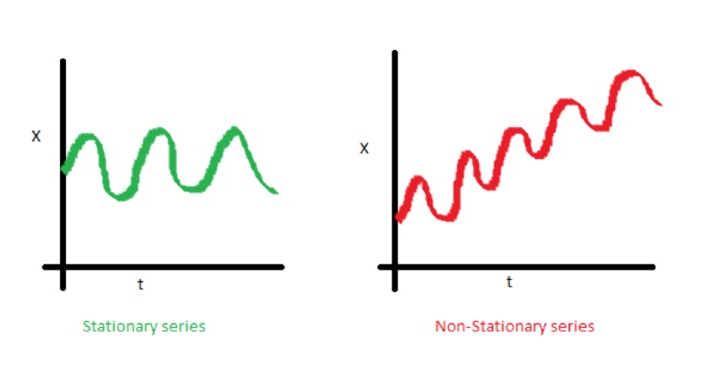
Exemples de processus stationnaires vs non stationnaires
Ligne de tendance
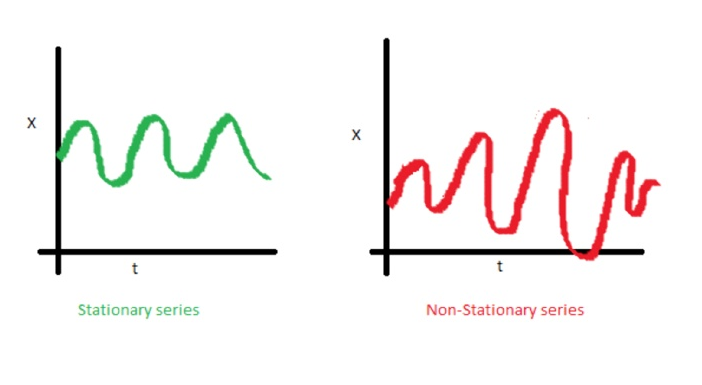
Dispersion
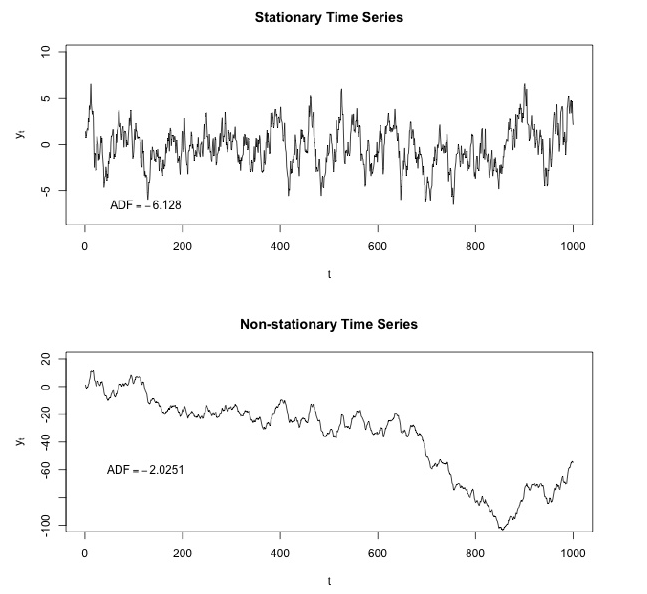
Le bruit blanc est un processus stationnaire stochastique qui peut être décrit en utilisant deux paramètres: la moyenne et la dispersion (variance). En temps discret, le bruit blanc est un signal discret dont les échantillons sont considérés comme une séquence de variables aléatoires non corrélées en série avec une moyenne nulle et une variance finie.
Si nous faisons une projection sur l'axe y, nous pouvons voir une distribution normale. Le bruit blanc est un processus gaussien dans le temps.
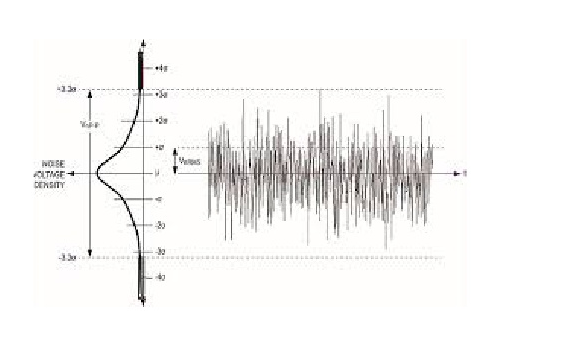
Dans la théorie des probabilités, la distribution normale (ou gaussienne) est une distribution de probabilité continue très courante. Les distributions normales sont importantes en statistique et sont souvent utilisées en sciences naturelles et sociales pour représenter des variables aléatoires à valeur réelle dont les distributions ne sont pas connues. La distribution normale est utile en raison du théorème de la limite centrale. Dans sa forme la plus générale, dans certaines conditions (qui incluent la variance finie), il indique que les moyennes d'échantillons d'observations de variables aléatoires tirées indépendamment de distributions indépendantes convergent en distribution vers la normale, c'est-à-dire deviennent normalement distribuées lorsque le nombre d'observations est suffisamment grand. Les quantités physiques qui devraient être la somme de nombreux processus indépendants (comme les erreurs de mesure) ont souvent des distributions presque normales. De plus, de nombreux résultats et méthodes (comme la propagation de l'incertitude et l'ajustement des paramètres des moindres carrés) peuvent être dérivés analytiquement sous une forme explicite lorsque les variables pertinentes sont normalement distribuées.
Supposons que nos données aient une tendance. Les pics qui l'entourent sont dus à de nombreux facteurs aléatoires, qui affectent nos données. Par exemple, le nombre de demandes traitées est très bien décrit en utilisant cette approche. Garbage collection, cache misses, paging by OS, beaucoup de choses affectent le temps particulier de réponse servie. Prenons une demi-heure de tranche de nos données, de 2017–08–27 de midi à 12h30. Nous pouvons voir que ces données ont une tendance, et quelques oscillations
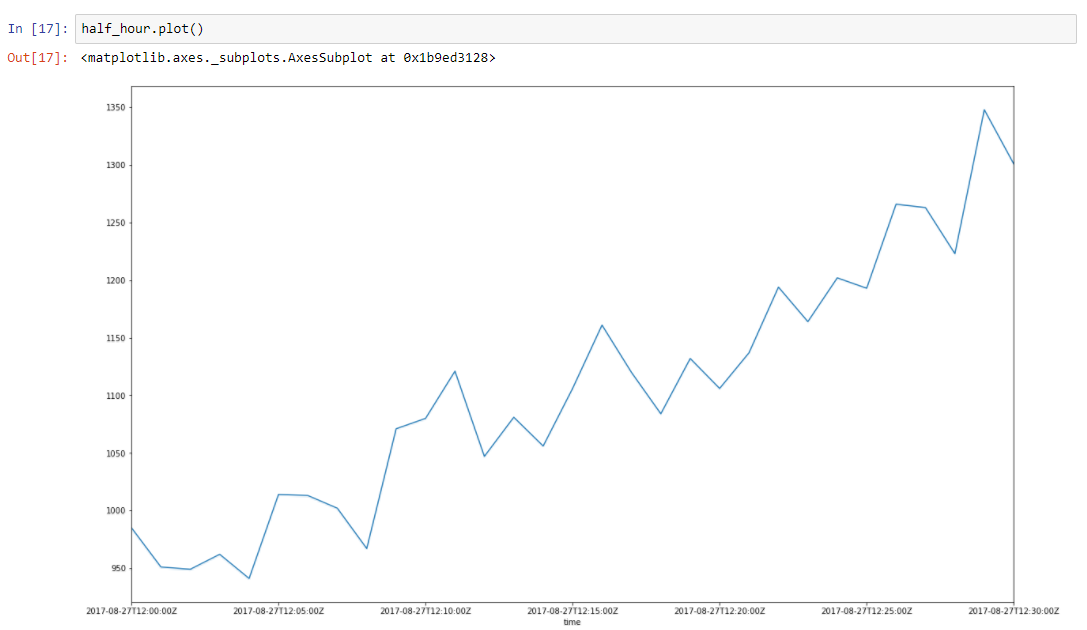
Construisons une ligne de régression pour définir la pente de cette ligne de tendance.
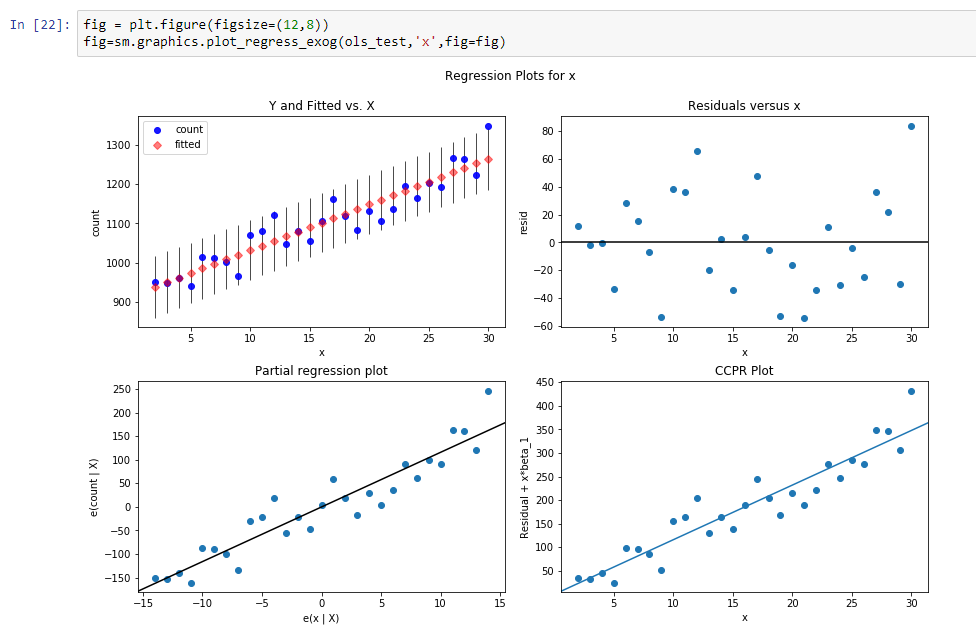
Les résultats de cette régression sont:
const 916.269951dy / dx 11.599507Les résultats signifient que const est un niveau pour cette ligne de tendance, et dy / dx est une ligne de pente qui définit la vitesse à laquelle le niveau augmente en fonction du temps.
Donc, en fait, nous réduisons la dimension des données de 31 paramètres à 2 paramètres. Si nous soustrayons de nos données initiales nos valeurs de fonction de régression, nous verrons un processus, qui ressemble à un processus stochastique stationnaire.
Ainsi, après soustraction, nous pouvons voir que la tendance a disparu et nous pouvons supposer que le processus est stochastique dans cette plage. Mais comment en être sûr.

Faisons
Dickey - test plus complet .
Dickey - Fuller teste l'hypothèse nulle selon laquelle la série chronologique a une racine et est également stationnaire ou rejette cette hypothèse. Si nous faisons le test de Dickey-Fuller sur notre tranche initiale, nous obtiendrons
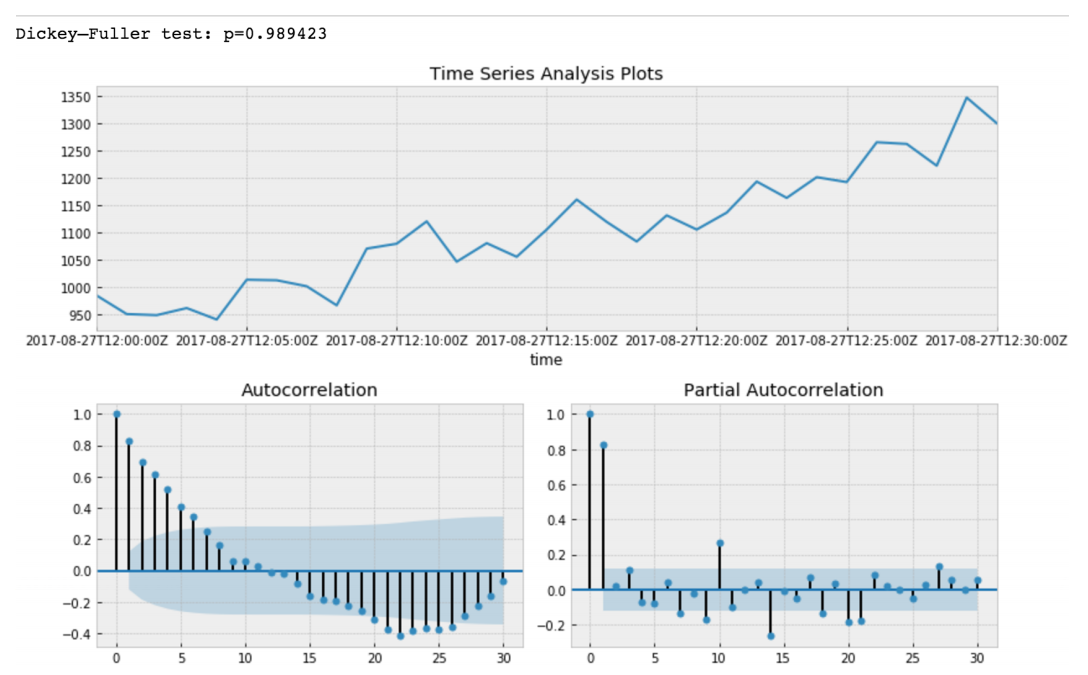
La valeur du test Dickey-Fuller rejette l'hypothèse nulle avec une forte confiance. Ainsi, notre tranche de séries chronologiques est non stationnaire. Et nous pouvons voir que la fonction d'autocorrélation montre les autocorrélations cachées.
Après soustraction de notre modèle de régression des données initiales.

Ici, nous pouvons voir que la valeur du test de Dickey-Fuller est vraiment petite et ne rejette pas une hypothèse nulle sur la non stationnarité de notre tranche de séries chronologiques. La fonction d'autocorrélation semble également bien.
Ainsi, nous avons effectué une certaine transformation de nos données et nous pouvons faire pivoter nos données en fonction de notre pente de notre ligne de tendance.
Régression segmentée des données
La régression segmentée , également connue sous le nom de
régression par morceaux ou «régression bâton cassé», est une méthode d'analyse de régression dans laquelle la variable indépendante est partitionnée en intervalles et un segment de ligne distinct est adapté à chaque intervalle. Une analyse de régression segmentée peut également être effectuée sur des données multivariées en partitionnant les différentes variables indépendantes. La régression segmentée est utile lorsque les variables indépendantes, regroupées en différents groupes, présentent des relations différentes entre les variables dans ces régions. Les limites entre les segments sont des points d'arrêt.
En fait, notre pente est une dérivée discrète de nos séries chronologiques non stationnaires en raison de l'intervalle constant de nos points métriques que nous ne pouvons pas prendre en compte dx. Par conséquent, nous pouvons approximer nos données comme une fonction par morceaux qui est calculée à l'aide de dérivées discrètes des tendances de régression des séries chronologiques.

Ci-dessus, une tranche de données du 26-08-2007 00.00 à 08.00
Il semble qu'il y ait une autocorrélation linéaire pour chaque tranche et si nous trouvons une ligne de régression pour chaque tranche, nous pouvons construire un modèle de nos tranches de temps en utilisant les hypothèses que nous avons faites.
En conséquence, nous aurons des données qui sont décrites en utilisant une quantité minimale de paramètres, ce qui est favorable en raison d'une meilleure généralisation. La dimension Vapnik - Chervonenkis doit être aussi petite que possible pour une bonne généralisation.
Dans la théorie Vapnik - Chervonenkis, la dimension VC (pour la dimension Vapnik - Chervonenkis) est une mesure de la capacité (complexité, puissance expressive, richesse ou flexibilité) d'un espace de fonctions qui peut être apprise par un algorithme de classification statistique. Elle est définie comme la cardinalité du plus grand ensemble de points que l'algorithme peut briser. Il a été initialement défini par Vladimir Vapnik et Alexey Chervonenkis.
Officiellement, la capacité d'un modèle de classification est liée à sa complexité. Par exemple, considérons le seuillage d'un polynôme de haut degré: si le polynôme est évalué au-dessus de zéro, ce point est classé comme positif, sinon comme négatif. Un polynôme de haut degré peut être ondulé, il peut donc bien s'adapter à un ensemble donné de points d'entraînement. Mais on peut s'attendre à ce que le classificateur fasse des erreurs sur d'autres points, car il est trop ondulé. Un tel polynôme a une capacité élevée. Une alternative beaucoup plus simple consiste à seuiller une fonction linéaire. Cette fonction peut ne pas convenir à l'ensemble d'entraînement, car elle a une faible capacité.
Par conséquent, nous avons approximé nos tranches horaires en utilisant une régression segmentée.
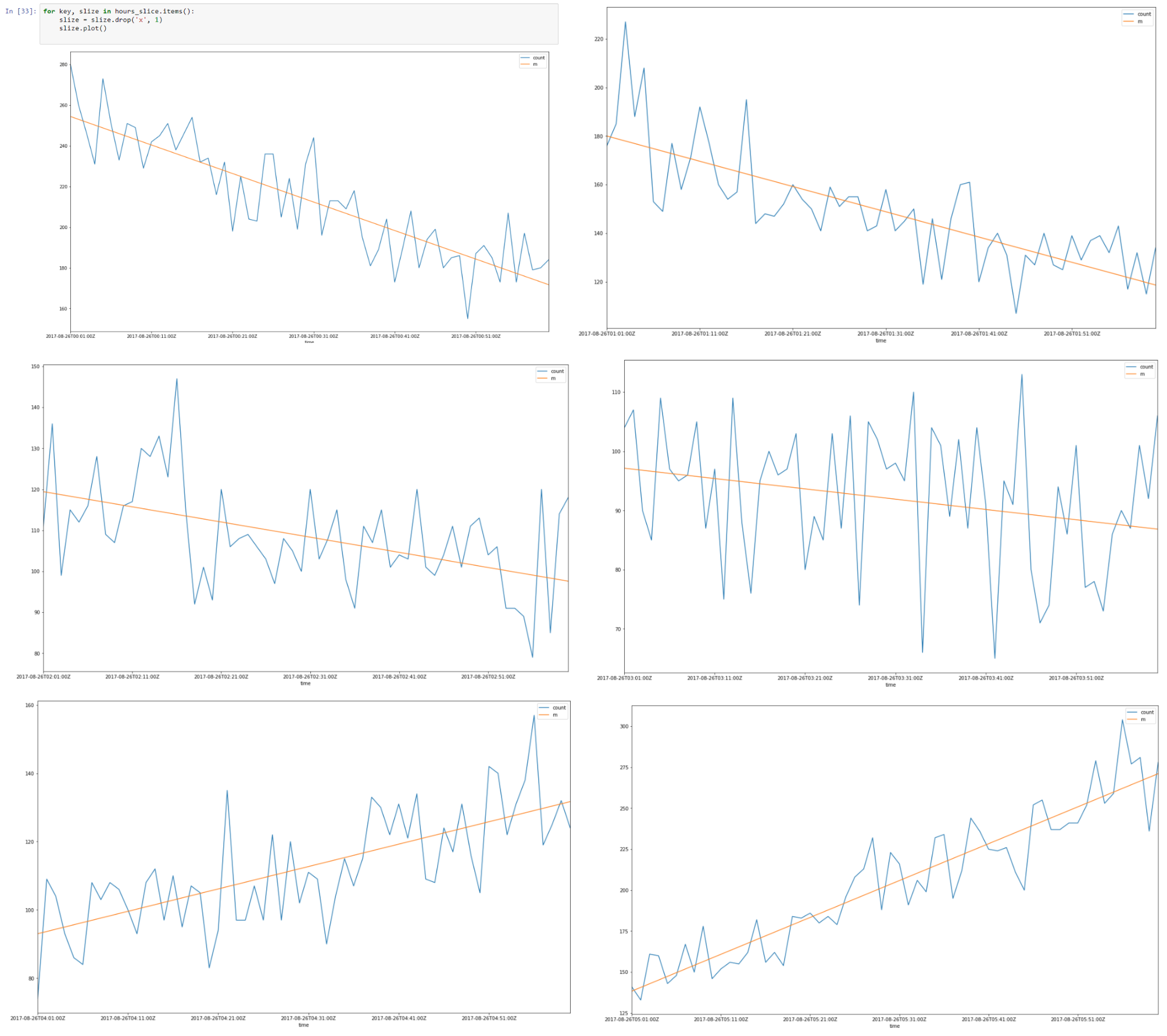
Assembler toutes les tranches de 8 heures

Et le rendre stochastique stationnaire en soustrayant le modèle de régression.
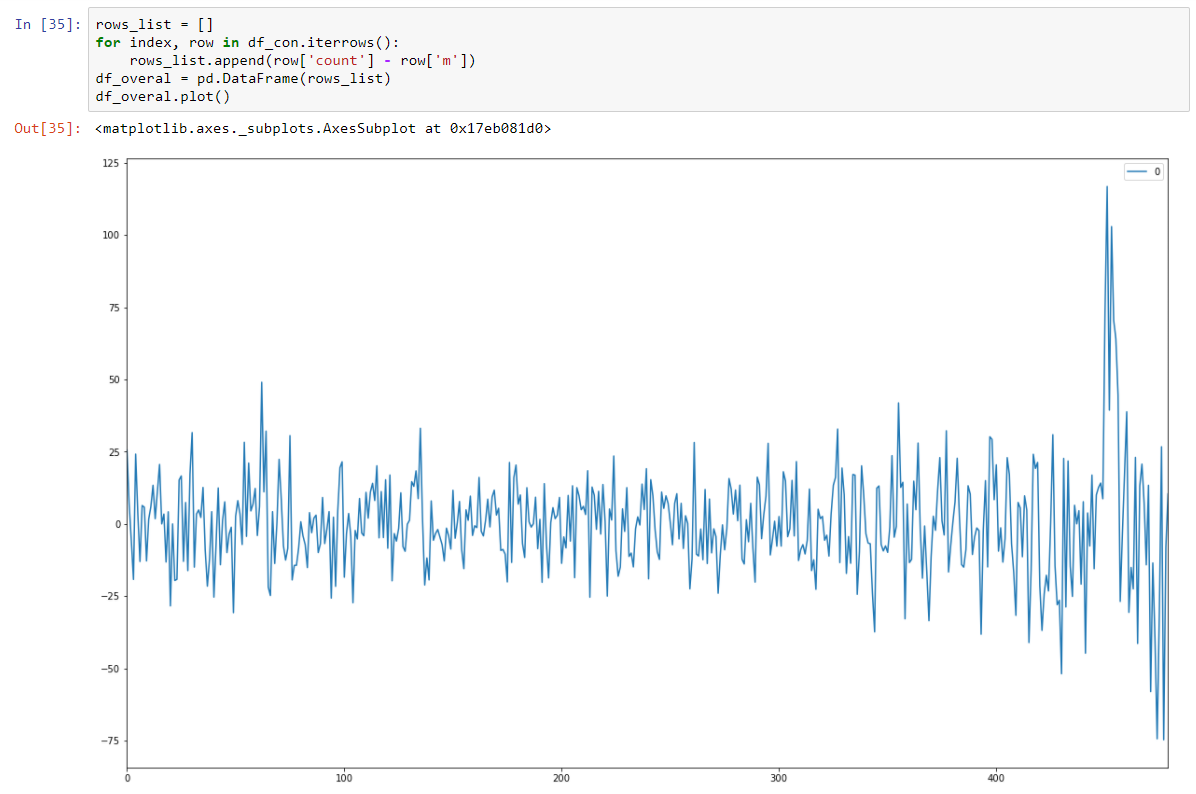
Et notre test Dickey-Fuller sur stationnaire montre avec une forte confiance que nous avons transformé nos données en séries stationnaires.
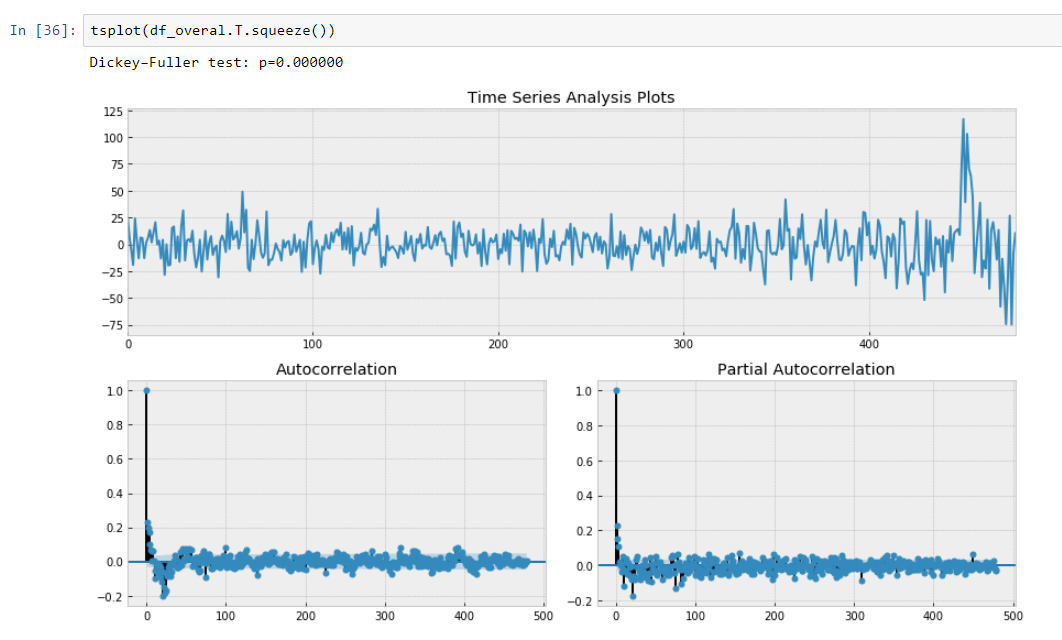
Nous avons donc un modèle de prédiction qui décrit nos données de séries chronologiques. Nous avons réduit la dimensionnalité de nos données 15/30 fois plus petites!
En fait, nous devons renvoyer la moyenne de la prédiction de notre modèle et la transformer à nouveau en utilisant le niveau et la pente pour une tranche particulière. Il minimisera la somme des erreurs quadratiques pour nos prédictions de modèles.
Mais nous devons également stocker la variance car l'augmentation de la variance pourrait conduire à la présence de nouveaux facteurs inconnus et comme nous le savons par la connaissance du domaine, il en est ainsi.
Il faut donc également alerter l'évolution rapide de la variance.
Nous voulons également utiliser le modèle ARIMA, mais une approche plus générale est préférable, et nous prévoyons de comparer ce modèle et l'ARIMA standard pour de meilleurs résultats. Voyons nos séries chronologiques (les verts sont des salves de variance sur les valeurs aberrantes)