🏇🏾 👨🏾‍🤝‍👨🏽 📇 Amélioration de l'agent Q-Learning basé sur les actions en ajoutant la récurrence et les récompenses 🏁 👨🏾‍✈️ 🤤

Rappel

Bonjour, Habr! J'attire votre attention sur une autre traduction de mon nouvel article à partir du médium .

La dernière fois ( premier article ) ( Habr ), nous avons créé un agent utilisant la technologie Q-Learning, qui effectue des transactions sur des séries temporelles d'échange simulées et réelles et essayé de vérifier si ce domaine de tâches est adapté à un apprentissage renforcé.

Cette fois, nous ajouterons une couche LSTM pour prendre en compte les dépendances temporelles au sein de la trajectoire et récompenser l'ingénierie de mise en forme basée sur les présentations.

Permettez-moi de vous rappeler que pour vérifier le concept, nous avons utilisé les données synthétiques suivantes:

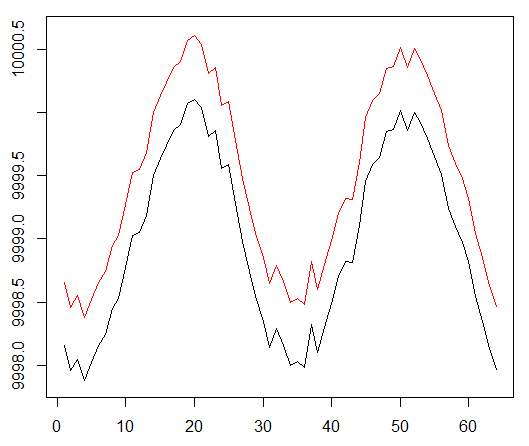
Données synthétiques: sinus avec bruit blanc.

La fonction sinus était le premier point de départ. Deux courbes simulent le prix d'achat et de vente d'un actif, où l'écart correspond au coût de transaction minimal.

Cependant, cette fois, nous voulons compliquer cette tâche simple en étendant le chemin d'attribution de crédit:

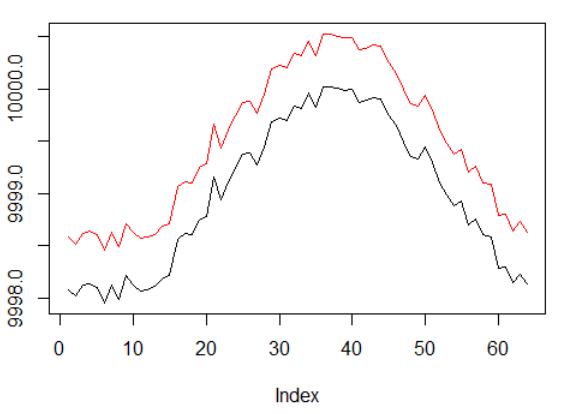
Données synthétiques: sinus avec bruit blanc.

La phase sinusale a été doublée.

Cela signifie que les rares récompenses que nous utilisons doivent s'étaler sur des trajectoires plus longues. De plus, nous réduisons considérablement la probabilité de recevoir une récompense positive, car l'agent a dû effectuer une séquence d'actions correctes 2 fois plus longtemps afin de surmonter les coûts de transaction. Les deux facteurs compliquent grandement la tâche de RL, même dans des conditions aussi simples qu'une onde sinusoïdale.

De plus, nous rappelons que nous avons utilisé cette architecture de réseau neuronal:

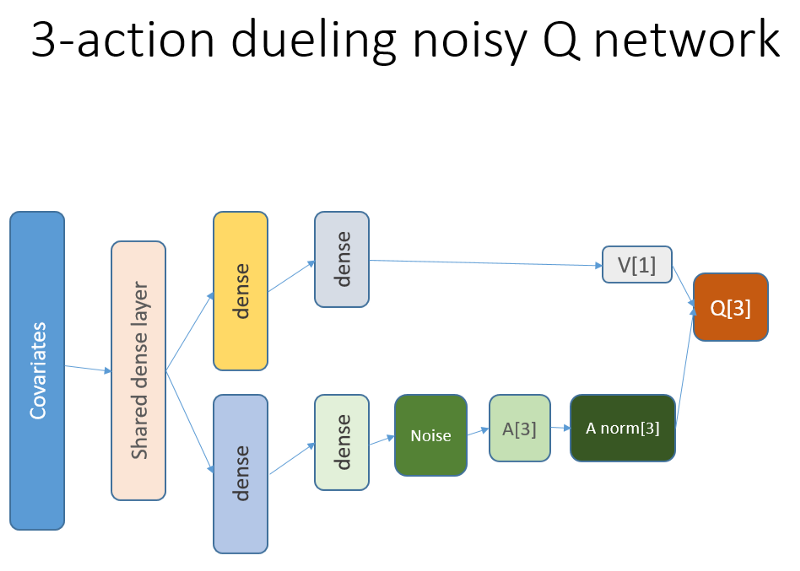
Ce qui a été ajouté et pourquoi

Lstm

Tout d'abord, nous voulions donner à l'agent une meilleure compréhension de la dynamique des changements au sein de la trajectoire. Autrement dit, l'agent devrait mieux comprendre son propre comportement: ce qu'il a fait en ce moment et pendant un certain temps dans le passé, et comment la distribution des actions de l'État, ainsi que les récompenses reçues, se sont développées. L'utilisation d'une couche de récurrence peut résoudre exactement ce problème. Bienvenue dans la nouvelle architecture utilisée pour lancer un nouvel ensemble d'expériences:

Veuillez noter que j'ai légèrement amélioré la description. La seule différence avec l'ancien NN est la première couche LSTM cachée au lieu d'une couche entièrement liée.

Veuillez noter qu'avec LSTM dans le travail, nous devons changer la sélection d'exemples d'expérience de reproduction pour la formation: maintenant nous avons besoin de séquences de transition au lieu d'exemples séparés. Voici comment cela fonctionne (c'est l'un des algorithmes). Nous avons utilisé l'échantillonnage ponctuel avant:

Le schéma fictif du tampon de lecture.

Nous utilisons ce schéma avec LSTM:

Maintenant, les séquences sont sélectionnées (dont nous spécifions empiriquement la longueur).

Comme auparavant, et maintenant l'échantillon est régulé par un algorithme de priorité basé sur des erreurs d'apprentissage temporo-temporel.

Le niveau de récurrence LSTM permet la diffusion directe des informations des séries chronologiques pour intercepter un signal supplémentaire caché dans les décalages passés. La série temporelle avec nous est un tenseur bidimensionnel de taille: la longueur de la séquence sur la représentation de notre état-action.

Présentations

L'ingénierie primée, Potential Based Reward Shaping (PBRS), basée sur le potentiel, est un outil puissant qui vous permet d'augmenter la vitesse, la stabilité et de ne pas violer l'optimalité du processus de recherche de politiques pour résoudre notre environnement. Je recommande de lire au moins ce document original sur le sujet:

people.eecs.berkeley.edu/~russell/papers/ml99-shaping.ps

Le potentiel détermine dans quelle mesure notre état actuel est relatif à l'état cible dans lequel nous voulons entrer. Une vue schématique de la façon dont cela fonctionne:

Il y a des options et des difficultés que vous pourriez comprendre après essais et erreurs, et nous omettons ces détails, vous laissant avec vos devoirs.

Il convient de mentionner une dernière chose, à savoir que le PBRS peut être justifié à l'aide de présentations, qui sont une forme de connaissance experte (ou simulée) sur le comportement presque optimal de l'agent dans l'environnement. Il existe un moyen de trouver de telles présentations pour notre tâche à l'aide de schémas d'optimisation. Nous omettons les détails de la recherche.

La récompense potentielle prend la forme suivante (équation 1):

r '= r + gamma * F (s') - F (s)

où F est le potentiel de l'État et r est la récompense initiale, gamma est le facteur d'actualisation (0: 1).

Avec ces réflexions, nous passons au codage.

Implémentation en R
Voici le code du réseau neuronal basé sur l'API Keras:

Code

# configure critic NN — — — — — — library('keras') library('R6') state_names_length <- 12 # just for example lstm_seq_length <- 4 learning_rate <- 1e-3 a_CustomLayer <- R6::R6Class( “CustomLayer” , inherit = KerasLayer , public = list( call = function(x, mask = NULL) { x — k_mean(x, axis = 2, keepdims = T) } ) ) a_normalize_layer <- function(object) { create_layer(a_CustomLayer, object, list(name = 'a_normalize_layer')) } v_CustomLayer <- R6::R6Class( “CustomLayer” , inherit = KerasLayer , public = list( call = function(x, mask = NULL) { k_concatenate(list(x, x, x), axis = 2) } , compute_output_shape = function(input_shape) { output_shape = input_shape output_shape[[2]] <- input_shape[[2]] * 3L output_shape } ) ) v_normalize_layer <- function(object) { create_layer(v_CustomLayer, object, list(name = 'v_normalize_layer')) } noise_CustomLayer <- R6::R6Class( “CustomLayer” , inherit = KerasLayer , lock_objects = FALSE , public = list( initialize = function(output_dim) { self$output_dim <- output_dim } , build = function(input_shape) { self$input_dim <- input_shape[[2]] sqr_inputs <- self$input_dim ** (1/2) self$sigma_initializer <- initializer_constant(.5 / sqr_inputs) self$mu_initializer <- initializer_random_uniform(minval = (-1 / sqr_inputs), maxval = (1 / sqr_inputs)) self$mu_weight <- self$add_weight( name = 'mu_weight', shape = list(self$input_dim, self$output_dim), initializer = self$mu_initializer, trainable = TRUE ) self$sigma_weight <- self$add_weight( name = 'sigma_weight', shape = list(self$input_dim, self$output_dim), initializer = self$sigma_initializer, trainable = TRUE ) self$mu_bias <- self$add_weight( name = 'mu_bias', shape = list(self$output_dim), initializer = self$mu_initializer, trainable = TRUE ) self$sigma_bias <- self$add_weight( name = 'sigma_bias', shape = list(self$output_dim), initializer = self$sigma_initializer, trainable = TRUE ) } , call = function(x, mask = NULL) { #sample from noise distribution e_i = k_random_normal(shape = list(self$input_dim, self$output_dim)) e_j = k_random_normal(shape = list(self$output_dim)) #We use the factorized Gaussian noise variant from Section 3 of Fortunato et al. eW = k_sign(e_i) * (k_sqrt(k_abs(e_i))) * k_sign(e_j) * (k_sqrt(k_abs(e_j))) eB = k_sign(e_j) * (k_abs(e_j) ** (1/2)) #See section 3 of Fortunato et al. noise_injected_weights = k_dot(x, self$mu_weight + (self$sigma_weight * eW)) noise_injected_bias = self$mu_bias + (self$sigma_bias * eB) output = k_bias_add(noise_injected_weights, noise_injected_bias) output } , compute_output_shape = function(input_shape) { output_shape <- input_shape output_shape[[2]] <- self$output_dim output_shape } ) ) noise_add_layer <- function(object, output_dim) { create_layer( noise_CustomLayer , object , list( name = 'noise_add_layer' , output_dim = as.integer(output_dim) , trainable = T ) ) } critic_input <- layer_input( shape = list(NULL, as.integer(state_names_length)) , name = 'critic_input' ) common_lstm_layer <- layer_lstm( units = 20 , activation = “tanh” , recurrent_activation = “hard_sigmoid” , use_bias = T , return_sequences = F , stateful = F , name = 'lstm1' ) critic_layer_dense_v_1 <- layer_dense( units = 10 , activation = “tanh” ) critic_layer_dense_v_2 <- layer_dense( units = 5 , activation = “tanh” ) critic_layer_dense_v_3 <- layer_dense( units = 1 , name = 'critic_layer_dense_v_3' ) critic_layer_dense_a_1 <- layer_dense( units = 10 , activation = “tanh” ) # critic_layer_dense_a_2 <- layer_dense( # units = 5 # , activation = “tanh” # ) critic_layer_dense_a_3 <- layer_dense( units = length(actions) , name = 'critic_layer_dense_a_3' ) critic_model_v <- critic_input %>% common_lstm_layer %>% critic_layer_dense_v_1 %>% critic_layer_dense_v_2 %>% critic_layer_dense_v_3 %>% v_normalize_layer critic_model_a <- critic_input %>% common_lstm_layer %>% critic_layer_dense_a_1 %>% #critic_layer_dense_a_2 %>% noise_add_layer(output_dim = 5) %>% critic_layer_dense_a_3 %>% a_normalize_layer critic_output <- layer_add( list( critic_model_v , critic_model_a ) , name = 'critic_output' ) critic_model_1 <- keras_model( inputs = critic_input , outputs = critic_output ) critic_optimizer = optimizer_adam(lr = learning_rate) keras::compile( critic_model_1 , optimizer = critic_optimizer , loss = 'mse' , metrics = 'mse' ) train.x <- array_reshape(rnorm(10 * lstm_seq_length * state_names_length) , dim = c(10, lstm_seq_length, state_names_length) , order = 'C') predict(critic_model_1, train.x) layer_name <- 'noise_add_layer' intermediate_layer_model <- keras_model(inputs = critic_model_1$input, outputs = get_layer(critic_model_1, layer_name)$output) predict(intermediate_layer_model, train.x)[1,] critic_model_2 <- critic_model_1

Déboguer votre décision sur votre conscience ...

Résultats et comparaison

Plongeons droit dans les résultats finaux. Remarque: tous les résultats sont des estimations ponctuelles et peuvent différer sur plusieurs séries avec différents couvercles de semences aléatoires.

La comparaison comprend:

version précédente sans LSTM et présentations
LSTM simple à 2 éléments
LSTM à 4 éléments
LSTM à 4 cellules avec récompenses PBRS générées

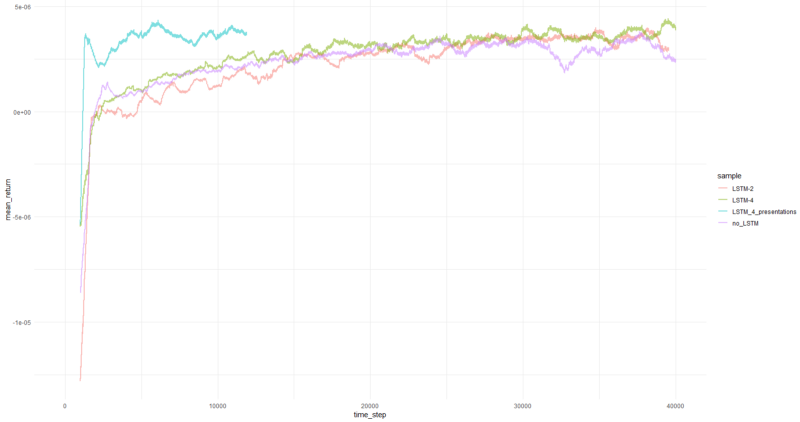
Le rendement moyen par épisode était en moyenne de 1 000 épisodes.

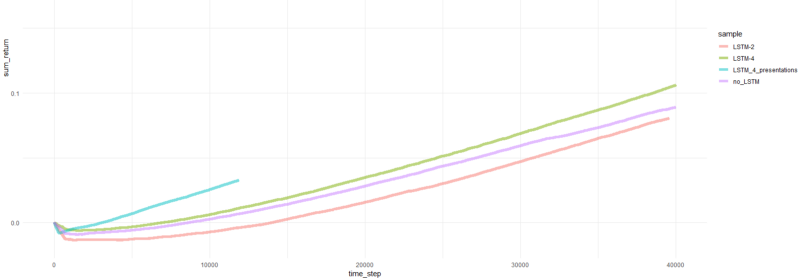
L'épisode total revient.

Graphiques de l'agent le plus performant:

Performances de l'agent.

Eh bien, il est assez évident que l'agent sous forme de PBRS converge si rapidement et de manière stable par rapport aux tentatives antérieures qu'il peut être accepté comme un résultat significatif. La vitesse est environ 4-5 fois plus élevée que sans présentations. La stabilité est merveilleuse.

En ce qui concerne l'utilisation de LSTM, 4 cellules ont donné de meilleurs résultats que 2 cellules. Un LSTM à 2 cellules a donné de meilleurs résultats qu'une version non LSTM (cependant, c'est peut-être l'illusion d'une seule expérience).

Les derniers mots

Nous avons vu que les récompenses récurrentes et de renforcement des capacités sont utiles. J'ai particulièrement apprécié la performance du PBRS.

Ne croyez pas quiconque me fait dire qu'il est facile de créer un agent RL qui converge bien, car c'est un mensonge. Chaque nouveau composant ajouté au système le rend potentiellement moins stable et nécessite beaucoup de configuration et de débogage.

Néanmoins, il est clair que la solution au problème peut être améliorée simplement en améliorant les méthodes utilisées (les données sont restées intactes). C'est un fait que pour n'importe quelle tâche, une certaine plage de paramètres fonctionne mieux que d'autres. Dans cette optique, vous vous lancez dans un parcours d'apprentissage réussi.

Je vous remercie