Bonjour à tous! Le développement de l'hexapode avance et enfin la partie mathématique de base a été testée et prête pour la documentation. Pour que le projet survive jusqu'au bout et ne ramasse pas de poussière sur l'étagère, vous devez voir ses changements positifs, même s'ils sont insignifiants. Dans cet article, je vais parler d'un algorithme pour résoudre le problème de la cinématique inverse et le démontrer en action. J'espère que ce sera intéressant.
Stades de développement:Partie 1 - ConceptionPartie 2 - AssemblagePartie 3 - CinématiquePartie 4 - Trajectoires et séquences mathématiquesPartie 5 - ÉlectroniquePartie 6 - transition vers l'impression 3DPartie 7 - Nouveaux logements, logiciels d'application et protocoles de communicationSystèmes de coordonnées
Pour commencer, il est nécessaire de déterminer les systèmes de coordonnées du robot - il y en a jusqu'à trois:
En fait, ils ne sont pas différents les uns des autres, mais sont situés à différents endroits du boîtier et peuvent être tournés les uns par rapport aux autres selon un certain angle. Vu de dessus, l'emplacement des axes sera le suivant (le paramètre coxa_zero_rotate sera décrit un peu plus loin):
Comme vous l'avez probablement déjà remarqué, les systèmes de coordonnées sur les côtés gauche et droit sont situés symétriquement par rapport au centre du corps. Il me semblait que ce serait plus facile.
Les coordonnées de chaque point sont définies par rapport au membre auquel ce point est destiné. Cette approche vous permet de déplacer sans douleur le membre n'importe où sans interférer avec la configuration.
Et donc ils sont situés par rapport au membre:
Les coordonnées du point cible sont relatives au MAIN COORDINATE SYSTEM. Au départ, je voulais définir les coordonnées par rapport au centre du boîtier, mais cela s'est avéré peu pratique et a nécessité le stockage d'un certain nombre de paramètres supplémentaires.
Ci-après, la notation X *, X **, etc. sera remplacé par X ′, X ′ ′.
Résolution du problème de cinématique inverse
Commençons par le moment le plus difficile et le plus intéressant pour moi - la cinématique. J'ai inventé l'algorithme moi-même, jetant parfois un coup d'œil aux propriétés d'un triangle et aux fonctions trigonométriques. Avec la mécanique, c'est difficile pour moi, et avec la trigonométrie c'est encore pire, donc peut-être quelque part je ne pourrais pas tenir compte de quelque chose, mais cet algorithme fonctionne (vidéo à la fin).
1. Énoncé du problème
Supposons que nous ayons besoin du membre avant droit pour atteindre le point A avec les coordonnées (150; -20; 100). On sait également que le membre est tourné de 45 degrés par rapport au corps (paramètre coxa_zero_rotate):
Le membre lui-même a les paramètres suivants:
Je pense que vous n'avez pas besoin de décrire ce que signifient ces paramètres, les noms parlent d'eux-mêmes. Vous pouvez seulement ajouter que tous ces paramètres sont déterminés par la configuration du boîtier, sont permanents et stockés dans la mémoire FLASH avec la possibilité d'éditer de l'extérieur (pour plus de flexibilité).
Voilà pourquoi vous en avez besoin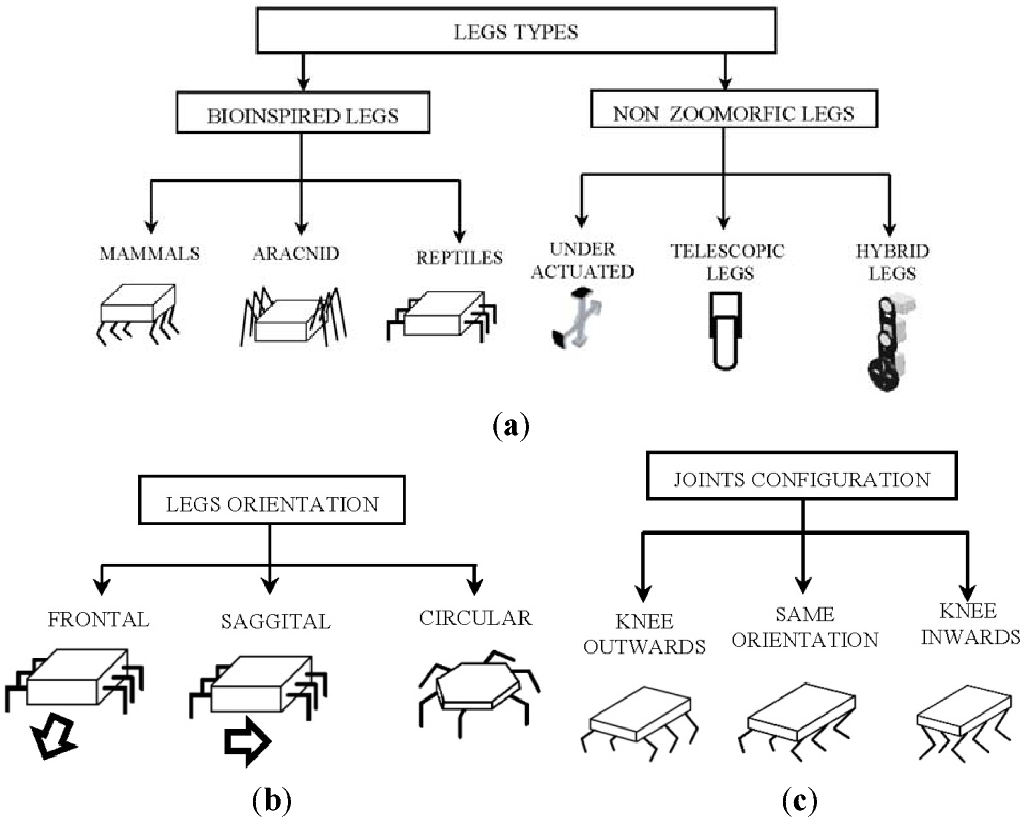
La photo montre différentes variations de la coque et l'emplacement des jambes de l'hexapode. Maintenant, il correspond à la configuration ARACNID. Supposons qu'il m'est venu à l'esprit de changer le cas en REPTILES, et pour cela, il sera assez simple de changer les valeurs des paramètres sans mesure dans le programme lui-même, même les points cibles n'auront pas à être modifiés (à moins bien sûr de l'approcher correctement).
Tous les paramètres ci-dessus sont suffisants pour résoudre le problème.
2. La solution au problème
2.1 Trouver l'angle de rotation de COXACette étape est la plus simple. Vous devez d'abord recalculer les coordonnées du point A par rapport au LIMB COORDINATE SYSTEM. De toute évidence, vous devez faire pivoter l'angle coxa_zero_rotate, vous pouvez le faire en utilisant les formules suivantes:
$$ afficher $$ x ′ = x ⋅ cos (α) + z ⋅ sin (α) = 150 ⋅ cos (45) + 100 ⋅ sin (45) = 176,78 $$ afficher $$
y′=y=−20
$$ afficher $$ z ′ = -x ⋅ sin (α) + z ⋅ cos (α) = -150 ⋅ sin (45) + 100 ⋅ cos (45) = -35,36 $$ afficher $$
Ainsi, nous avons obtenu les coordonnées du point cible A (176,78; -20; -35,36) par rapport au LIMB COORDINATE SYSTEM.
Vous pouvez maintenant trouver l'angle COXA en utilisant la fonction atan2:
COXA=atan2(z′,x′)=atan2(−35,36,176,78)=−11,30°
Et donc, nous avons obtenu l'angle selon lequel vous devez faire tourner le servo COXA de sorte que le point A soit dans le plan X'Y '. Voyons maintenant nos calculs dans KOMPAS 3D:
D'accord.
2.2 Trouver l'angle de rotation de FEMUR et TIBIAPour trouver ces angles, il faut aller dans le plan X'Y '. Pour aller dans l'avion, vous devez faire pivoter le point de l'angle COXA, que nous avons déjà calculé plus tôt.
$$ afficher $$ x ′ = x ′ ⋅ cos (α) + y ′ ⋅ sin (α) = 176,78 ⋅ cos (-11) + -20 ⋅ sin (-11) = 180,28 $$ afficher $$
y′=y=−20
La coordonnée
y ' ne change pas, car nous tournons le long de l'axe Y'.
Ensuite, vous devez supprimer la longueur COXA du calcul, c'est-à-dire on passe au plan X''Y '', pour cela on effectue un décalage de la coordonnée
x 'du point de la longueur COXA:
x′′=x′−coxaLength=180,28−40=140,28
y′′=y′
Après toutes ces manipulations, la solution du problème se résume à trouver les angles
a et
b du triangle:
Avant de trouver les angles, vous devez trouver le troisième côté C de ce triangle. Cette distance n'est rien d'autre que la longueur du vecteur et est calculée par la formule:
$$ afficher $$ C = \ sqrt {x ′ ′ ^ 2 + y ′ ′ ^ 2} = \ sqrt {140,28 ^ 2 + (-20) ^ 2} = 141,70 $$ afficher $$
Vous devez maintenant vérifier si le membre peut atteindre ce point. Si C est supérieur à la somme des longueurs de FEMUR et TIBIA, alors le point n'est pas accessible. Dans notre cas, 141,70 <141 + 85 - le point est accessible.
Maintenant, nous connaissons tous les côtés du triangle et nous pouvons trouver les angles
a et
b dont nous avons besoin en utilisant le théorème du cosinus:
a=acos(A2+C2−B2 over2AC)=72,05°
b=acos(B2+A2−C2 sur2BA)=72,95°
Les angles obtenus ne sont pas applicables pour les alimenter aux servos, car cela ne prend pas en compte la position initiale et l'angle d'inclinaison de la droite C vers l'axe X. Si nous connaissons les angles initiaux FEMUR et TIBIA (135 ° et 45 °), alors l'angle d'inclinaison C vers l'axe X n'est pas connu. Vous pouvez le trouver en utilisant la fonction atan2 (y ′ ′, x ′ ′):
$$ affichage $$ φ = atan2 (y ′ ′, x ′ ′) = atan2 (-20, 140,28) = -8,11 ° $$ affichage $$
Enfin, vous pouvez calculer l'angle de rotation des servos FEMUR et TIBIA:
FEMUR=femurZeroRotate−a−φ=135−72.05+8.11=71.06°
FEMUR=b−tibiaZeroRotate=45−72,95=27,95°
Vérifions nos calculs:
Cela semble être la vérité.
Résumé
Les angles calculés COXA, FEMUR et TIBIA conviennent pour alimenter leurs servos. Vous remarquerez peut-être que l'angle COXA est négatif et, par conséquent, la question se pose: «Comment faire tourner le variateur de -11,3 degrés?». L'astuce est que j'utilise la position neutre du servo COXA comme un zéro logique, cela permet au variateur de faire pivoter les angles positifs et négatifs. C'est bien sûr évident, mais je pense qu'il ne serait pas déplacé de le mentionner. J'en parlerai plus en détail dans les articles suivants lorsque je parlerai de la mise en œuvre de tout ce qui précède.
Code source
Assez de mots, laissez-moi voir le code#define RAD_TO_DEG(rad) ((rad) * 180.0 / M_PI) #define DEG_TO_RAD(deg) ((deg) * M_PI / 180.0) typedef enum { LINK_COXA, LINK_FEMUR, LINK_TIBIA } link_id_t; typedef struct {
Algorithme en action
Puis, par hasard, une séquence est apparue qui rappelait quelque peu une danse
PS
Je serais heureux si quelqu'un pouvait simplifier cet algorithme. Je l'ai fait pour que je puisse le comprendre après, disons, une demi-année.