À notre époque, les machines ont réussi à atteindre 99% de précision dans la compréhension et la définition des caractéristiques et des objets dans les images. Nous sommes confrontés à cela tous les jours, par exemple: la reconnaissance faciale dans l'appareil photo du smartphone, la possibilité de rechercher des photos sur google, de scanner du texte à partir d'un code à barres ou de livres à une bonne vitesse, etc. le réseau. Si vous êtes un passionné d'apprentissage en profondeur, vous en avez probablement entendu parler et vous pourriez développer plusieurs classificateurs d'images. Les frameworks modernes d'apprentissage en profondeur tels que Tensorflow et PyTorch simplifient l'apprentissage automatique d'images. Cependant, la question demeure: comment les données passent-elles à travers les couches du réseau neuronal et comment l'ordinateur en tire-t-il des leçons? Pour obtenir une vue claire à partir de zéro, nous plongons dans une convolution, en visualisant l'image de chaque couche.

Réseaux de neurones convolutifs
Avant de commencer à étudier les réseaux de neurones convolutifs (SNA), vous devez apprendre à travailler avec les réseaux de neurones. Les réseaux de neurones imitent le cerveau humain pour résoudre des problèmes complexes et rechercher des modèles dans les données. Au cours des dernières années, ils ont remplacé de nombreux algorithmes d'apprentissage automatique et de vision par ordinateur. Le modèle de base d'un réseau neuronal est constitué de neurones organisés en couches. Chaque réseau de neurones a une couche d'entrée et de sortie et plusieurs couches cachées qui lui sont ajoutées en fonction de la complexité du problème. Lors de la transmission de données à travers des couches, les neurones sont entraînés et reconnaissent les signes. Cette représentation d'un réseau neuronal s'appelle un modèle. Une fois le modèle formé, nous demandons au réseau de faire des prévisions sur la base des données de test.
Le SNS est un type spécial de réseau de neurones qui fonctionne bien avec les images. Ian Lekun les a proposés en 1998, où ils ont reconnu le nombre présent dans l'image d'entrée. Le SNA est également utilisé pour la reconnaissance vocale, la segmentation d'images et le traitement de texte. Avant la création de réseaux de neurones convolutifs, des perceptrons multicouches étaient utilisés dans la construction de classificateurs d'images. La classification des images fait référence à la tâche d'extraction des classes d'une image raster multicanal (couleur, noir et blanc). Les perceptrons multicouches mettent beaucoup de temps à rechercher des informations dans les images, car chaque entrée doit être associée à chaque neurone de la couche suivante. Le SCN les a contournés en utilisant un concept appelé connectivité locale. Cela signifie que nous connecterons chaque neurone uniquement à la région d'entrée locale. Cela minimise le nombre de paramètres, permettant à diverses parties du réseau de se spécialiser dans des attributs de haut niveau tels que la texture ou le motif répétitif. Confus? Comparons la façon dont les images sont transmises à travers les perceptrons multicouches (MP) et les réseaux de neurones convolutifs.
Comparaison de MP et SNA
Le nombre total d'entrées dans la couche d'entrée pour le perceptron multicouche sera de 784, car l'image d'entrée a une taille de 28x28 = 784 (l'ensemble de données MNIST est pris en compte). Le réseau doit être en mesure de prédire le nombre dans l'image d'entrée, ce qui signifie que la sortie peut appartenir à l'une des classes suivantes dans la plage de 0 à 9. Dans la couche de sortie, nous renvoyons des estimations de classe, par exemple, si cette entrée est l'image avec le numéro «3», puis dans la couche de sortie, le neurone "3" correspondant a une valeur plus élevée que les autres neurones. Encore une fois, la question se pose: "De combien de couches cachées avons-nous besoin et combien de neurones doivent être dans chacune?" Par exemple, prenez le code MP suivant:
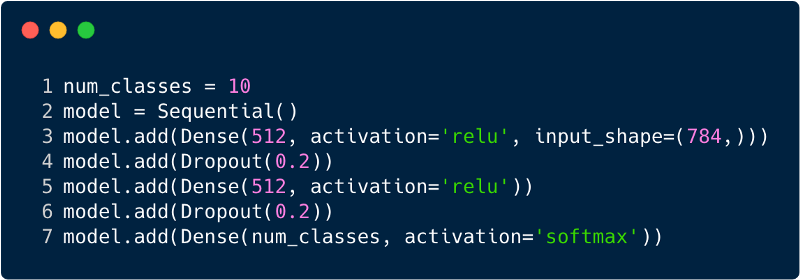
Le code ci-dessus est implémenté à l'aide d'un framework appelé Keras. La première couche cachée a 512 neurones qui sont connectés à la couche d'entrée de 784 neurones. La prochaine couche cachée: la couche d'exclusion, qui résout le problème du recyclage. 0,2 signifie qu'il y a 20% de chances de ne pas prendre en compte les neurones de la couche cachée précédente. Nous avons à nouveau ajouté une deuxième couche cachée avec le même nombre de neurones que dans la première couche cachée (512), puis une autre couche exclusive. Enfin, terminer cet ensemble de couches avec une couche de sortie composée de 10 classes. La classe qui compte le plus sera le nombre prévu par le modèle. Voici à quoi ressemble un réseau multicouche après avoir identifié toutes les couches. L'un des inconvénients du perceptron à plusieurs niveaux est qu'il est entièrement connecté, ce qui prend beaucoup de temps et d'espace.
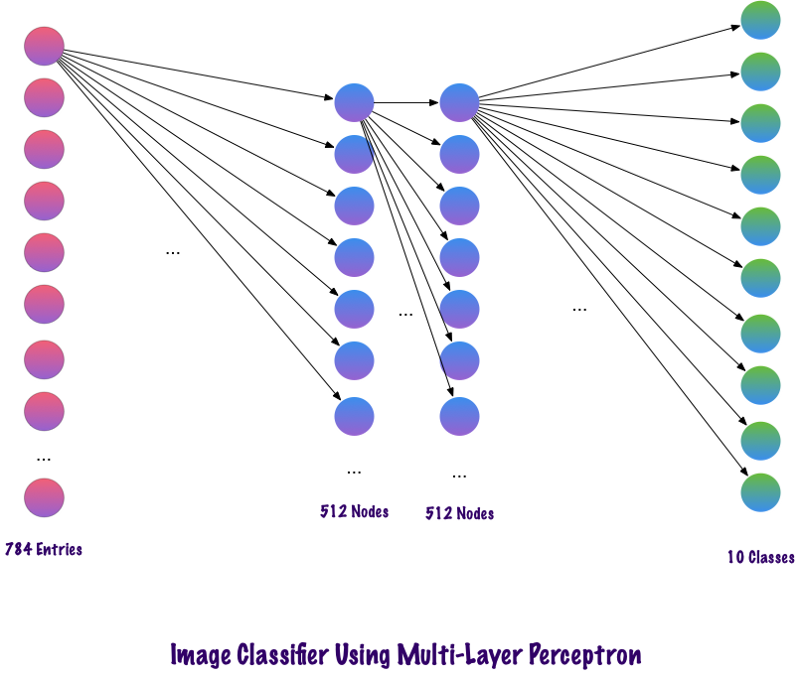
Les convoltes n'utilisent pas de couches entièrement connectées. Ils utilisent des couches clairsemées, qui prennent des matrices en entrée, ce qui donne un avantage sur MP. Dans MP, chaque nœud est responsable de la compréhension de l'ensemble de l'image. Dans le SCN, nous divisons l'image en zones (petites zones locales de pixels). La couche de sortie combine les données reçues de chaque nœud caché pour trouver des modèles. Voici une image de la façon dont les couches sont connectées.
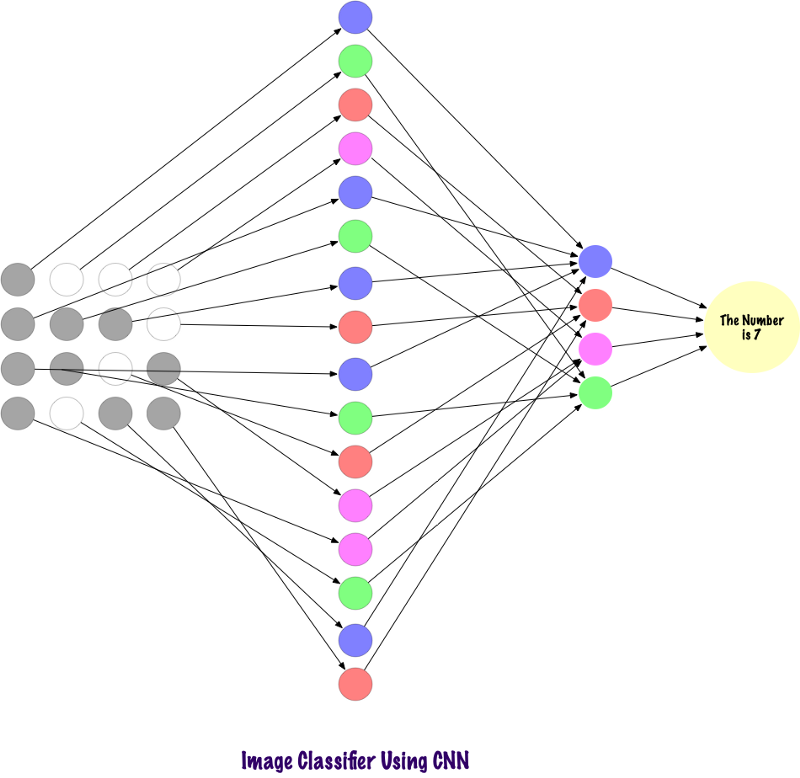
Voyons maintenant comment le SCN trouve des informations sur les photos. Avant cela, nous devons comprendre comment les signes sont extraits. Dans le SCN, nous utilisons différentes couches, chaque couche préserve les signes de l'image, par exemple, elle prend en compte l'image du chien, lorsque le réseau a besoin de classer le chien, elle doit identifier tous les signes, tels que les yeux, les oreilles, la langue, les jambes, etc. Ces signes sont brisés et reconnus au niveau du réseau local à l'aide de filtres et de cœurs.
Comment les ordinateurs regardent-ils une image?
Une personne qui regarde une image et en comprend le sens semble très raisonnable. Disons que vous marchez et remarquez les nombreux paysages qui vous entourent. Comment comprenons-nous la nature dans ce cas? Nous prenons des photos de l'environnement en utilisant notre principal organe sensoriel - l'œil, puis nous l'envoyons à la rétine. Tout cela semble assez intéressant, non? Imaginons maintenant qu'un ordinateur fasse de même. Dans les ordinateurs, les images sont interprétées à l'aide d'un ensemble de valeurs de pixels allant de 0 à 255. L'ordinateur examine ces valeurs de pixels et les comprend. À première vue, il ne connaît pas les objets et les couleurs. Il reconnaît simplement les valeurs de pixels et l'image est équivalente à un ensemble de valeurs de pixels pour l'ordinateur. Plus tard, en analysant les valeurs des pixels, il apprend progressivement si l'image est grise ou couleur. Les images en niveaux de gris n'ont qu'un seul canal, car chaque pixel représente l'intensité d'une couleur. 0 signifie noir et 255 signifie blanc, les autres variantes du noir et blanc, c'est-à-dire du gris, sont entre elles.
Les images en couleur ont trois canaux, rouge, vert et bleu. Ils représentent l'intensité de 3 couleurs (matrice tridimensionnelle), et lorsque les valeurs changent simultanément, cela donne un large éventail de couleurs, vraiment une palette de couleurs! Après cela, l'ordinateur reconnaît les courbes et les contours des objets dans l'image. Tout cela peut être étudié dans le réseau neuronal convolutif. Pour cela, nous utiliserons PyTorch pour charger un ensemble de données et appliquer des filtres aux images. Voici un extrait de code.
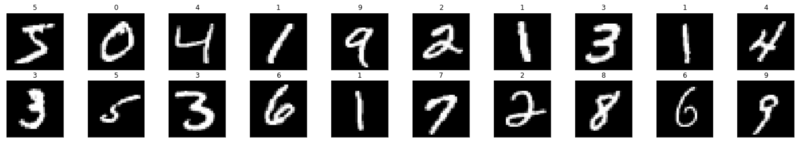
Voyons maintenant comment une seule image est introduite dans un réseau neuronal.
img = np.squeeze(images[7]) fig = plt.figure(figsize = (12,12)) ax = fig.add_subplot(111) ax.imshow(img, cmap='gray') width, height = img.shape thresh = img.max()/2.5 for x in range(width): for y in range(height): val = round(img[x][y],2) if img[x][y] !=0 else 0 ax.annotate(str(val), xy=(y,x), color='white' if img[x][y]<thresh else 'black')

C'est ainsi que le nombre «3» est divisé en pixels. À partir de l'ensemble des chiffres manuscrits, «3» est sélectionné au hasard, dans lequel les valeurs des pixels sont affichées. Ici, ToTensor () normalise les valeurs réelles des pixels (0–255) et les limite à une plage de 0 à 1. Pourquoi est-ce? Parce qu'il facilite les calculs dans les sections suivantes, soit pour interpréter des images, soit pour trouver des modèles communs qui y existent.
Créez votre propre filtre
Filtre, comme son nom l'indique, filtre les informations. Dans le cas des réseaux de neurones convolutifs, lorsque vous travaillez avec des images, les informations sur les pixels sont filtrées. Pourquoi devrions-nous filtrer? N'oubliez pas qu'un ordinateur doit passer par un processus d'apprentissage pour comprendre les images, très similaire à la façon dont un enfant le fait. Dans ce cas, cependant, nous n'aurons pas besoin de plusieurs années! Bref, il apprend à partir de zéro puis progresse vers l'ensemble.
Par conséquent, le réseau doit initialement connaître toutes les parties grossières de l'image, à savoir les bords, les contours et autres éléments de bas niveau. Une fois découverts, le chemin des symptômes complexes est ouvert. Pour y accéder, nous devons d'abord extraire les attributs de bas niveau, puis ceux du milieu, puis ceux de niveau supérieur. Les filtres sont un moyen d'extraire les informations dont l'utilisateur a besoin, et pas seulement un transfert de données aveugle, à cause duquel l'ordinateur ne comprend pas la structuration des images. Au début, les fonctions de bas niveau peuvent être extraites en fonction d'un filtre spécifique. Le filtre ici est également un ensemble de valeurs de pixels, semblable à une image. Il peut être compris comme les poids qui relient les couches du réseau neuronal convolutif. Ces poids ou filtres sont multipliés par des valeurs d'entrée pour produire des images intermédiaires qui représentent la compréhension informatique de l'image. Ensuite, ils sont multipliés par quelques filtres supplémentaires pour étendre la vue. Ensuite, il détecte les organes visibles d'une personne (à condition qu'une personne soit présente dans l'image). Plus tard, avec l'inclusion de plusieurs filtres et plusieurs couches, l'ordinateur s'exclame: «Oh, oui! Ceci est un homme. "
Si nous parlons de filtres, nous avons de nombreuses options. Vous pouvez vouloir flouter l'image, puis appliquer un filtre de flou, si vous devez ajouter de la netteté, un filtre de netteté viendra à la rescousse, etc.
Examinons quelques extraits de code pour comprendre la fonctionnalité des filtres.
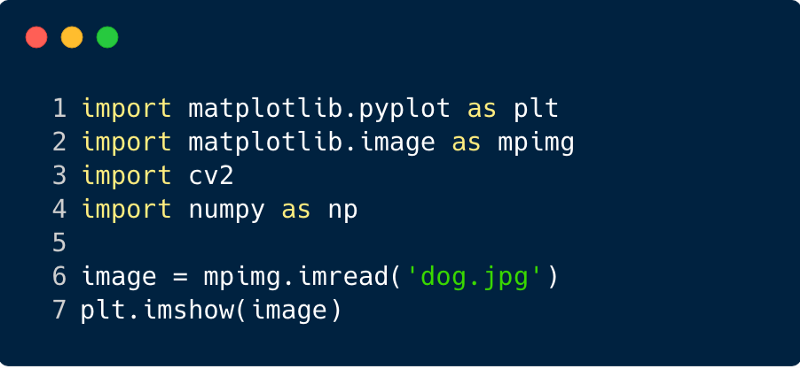

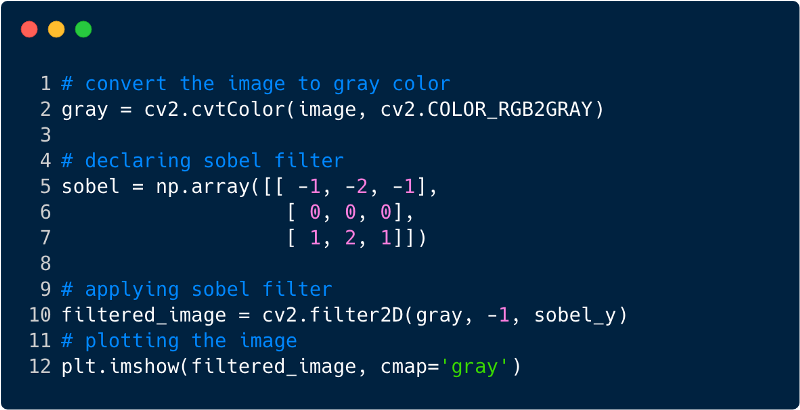

Voici à quoi ressemble l'image après avoir appliqué le filtre, dans ce cas, nous avons utilisé le filtre Sobel.
Réseaux de neurones convolutifs
Jusqu'à présent, nous avons vu comment les filtres sont utilisés pour extraire les fonctionnalités des images. Maintenant, pour compléter l'ensemble du réseau de neurones convolutionnels, nous devons connaître toutes les couches que nous utilisons pour le concevoir. Les couches utilisées dans le SCN,
- Couche convolutionnelle
- Couche de mise en commun
- Couche entièrement collée
Avec les trois couches, le classificateur d'images convolutionnel ressemble à ceci:
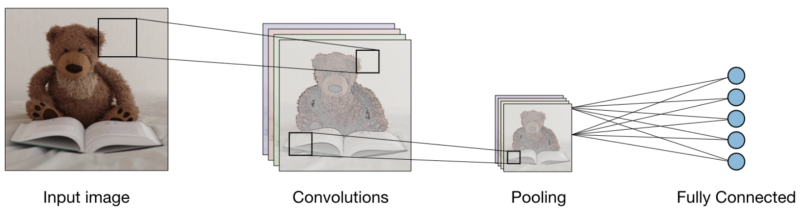
Voyons maintenant ce que fait chaque couche.
La couche convolutionnelle (CONV) utilise des filtres qui effectuent des opérations de convolution en balayant l'image d'entrée. Ses hyperparamètres incluent une taille de filtre, qui peut être 2x2, 3x3, 4x4, 5x5 (mais sans s'y limiter) et l'étape S. Le résultat O est appelé une carte d'entités ou une carte d'activation dans laquelle toutes les entités sont calculées à l'aide de couches d'entrée et de filtres. Vous trouverez ci-dessous une image de la génération de cartes d'entités lors de l'application de la convolution,
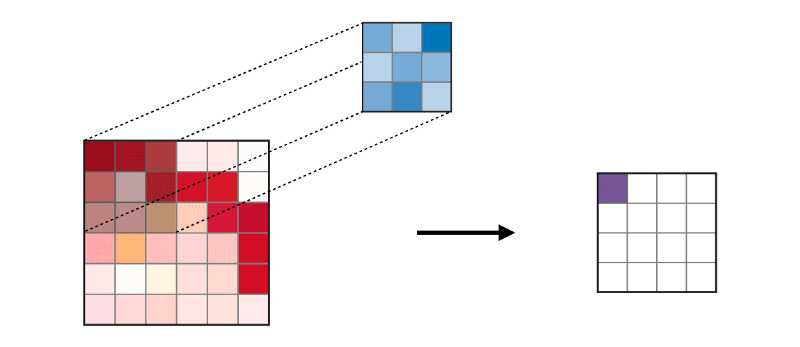 La couche de fusion (POOL) est
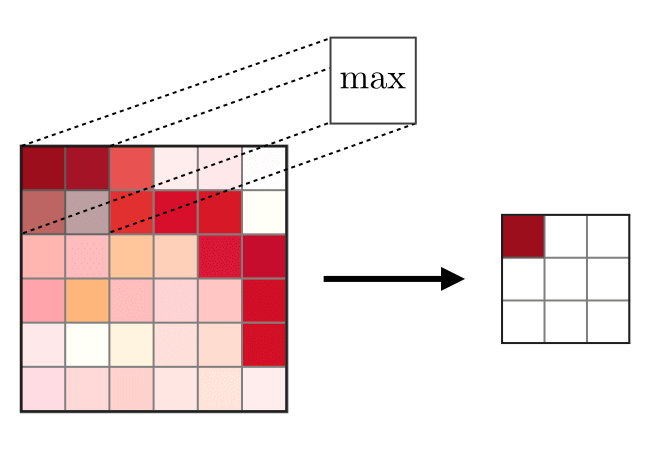
La couche de fusion (POOL) est utilisée pour compacter les entités généralement utilisées après la couche de convolution. Il existe deux types d'opérations syndicales - il s'agit de l'union maximale et moyenne, où les valeurs maximales et moyennes des caractéristiques sont prises, respectivement. Ce qui suit est le fonctionnement des opérations de fusion,
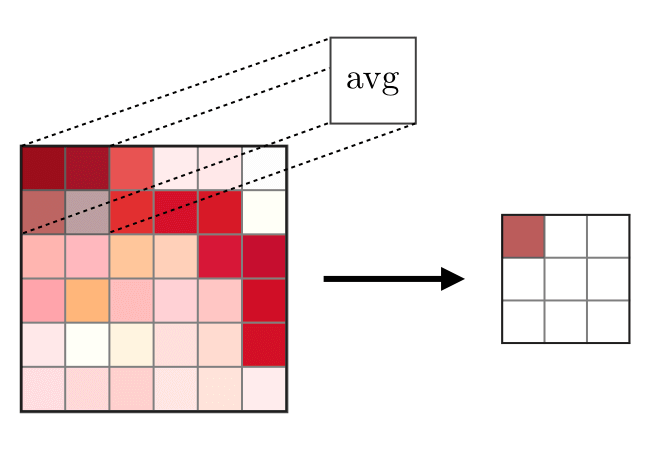 Les couches entièrement connectées (FC)
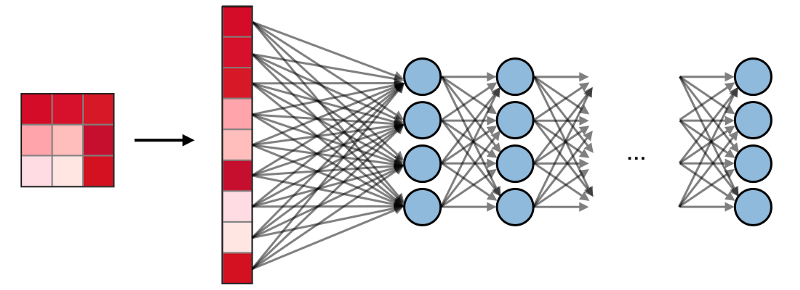
Les couches entièrement connectées (FC) fonctionnent avec une entrée plate, où chaque entrée est connectée à tous les neurones. Ils sont généralement utilisés à la fin du réseau pour connecter les couches cachées à la couche de sortie, ce qui permet d'optimiser les scores de classe.
Visualisation SNA dans PyTorch
Maintenant que nous avons l'idéologie complète de la construction du SNA, implémentons le SNA en utilisant le cadre PyTorch de Facebook.
Étape 1 : Téléchargez l'image d'entrée à envoyer sur le réseau. (Ici, nous le faisons avec Numpy et OpenCV)
import cv2 import matplotlib.pyplot as plt %matplotlib inline img_path = 'dog.jpg' bgr_img = cv2.imread(img_path) gray_img = cv2.cvtColor(bgr_img, cv2.COLOR_BGR2GRAY)
 Étape 2
Étape 2 : Filtres de rendu
Visualisons les filtres pour mieux comprendre ceux que nous utiliserons,
import numpy as np filter_vals = np.array([ [-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1] ]) print('Filter shape: ', filter_vals.shape)
 Étape 3
Étape 3 : déterminer le SCN
Ce SCN a une couche convolutionnelle et une couche de mise en commun avec une fonction maximale, et les poids sont initialisés à l'aide des filtres montrés ci-dessus,
import torch import torch.nn as nn import torch.nn.functional as F class Net(nn.Module): def __init__(self, weight): super(Net, self).__init__()
Net( (conv): Conv2d(1, 4, kernel_size=(4, 4), stride=(1, 1), bias=False) (pool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False) )
Étape 4 : Filtres de rendu
Un regard rapide sur les filtres utilisés,
def viz_layer(layer, n_filters= 4): fig = plt.figure(figsize=(20, 20)) for i in range(n_filters): ax = fig.add_subplot(1, n_filters, i+1) ax.imshow(np.squeeze(layer[0,i].data.numpy()), cmap='gray') ax.set_title('Output %s' % str(i+1)) fig = plt.figure(figsize=(12, 6)) fig.subplots_adjust(left=0, right=1.5, bottom=0.8, top=1, hspace=0.05, wspace=0.05) for i in range(4): ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[]) ax.imshow(filters[i], cmap='gray') ax.set_title('Filter %s' % str(i+1)) gray_img_tensor = torch.from_numpy(gray_img).unsqueeze(0).unsqueeze(1)
Filtres:
 Étape 5
Étape 5 : résultats filtrés par couche
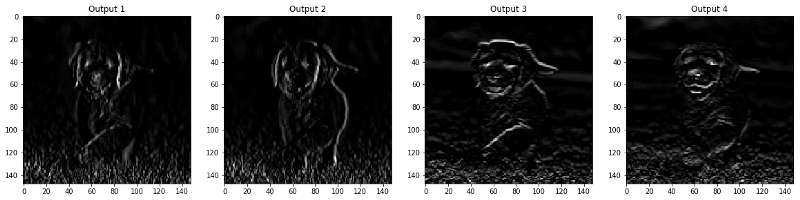
Les images qui apparaissent dans les couches CONV et POOL sont présentées ci-dessous.
viz_layer(activated_layer) viz_layer(pooled_layer)
Couches convolutives

Regroupement des couches
 Source
Source