L'énoncé du problème

L'autre jour, je surfais sur Internet et une chose assez curieuse a retenu mon attention: le moteur Mendocino . C'est un rotor à roulement à très faible friction: l'original avait un cylindre en verre suspendu à deux aiguilles, mais les modernes utilisent une suspension magnétique. C'est un moteur sans balais: le rotor est doté de batteries solaires qui génèrent du courant pour les bobines enroulées autour du rotor. Le rotor tourne dans un champ magnétique fixe, les batteries solaires étant exposées à la source de lumière l'une après l'autre. C'est une solution assez élégante qu'il est très possible de recréer chez soi.

Voici la vidéo qui explique comment cela fonctionne (en russe):


Mais cette vidéo avait une autre curiosité encore plus forte que le moteur lui-même. Dans la description de la vidéo, Dmitry Korzhevsky écrit: «Vous NE POUVEZ PAS remplacer le support latéral par un aimant! Ne me posez plus de questions à ce sujet! »

Avertissement: je ne suis pas un expert en physique et je peux me tromper sur certains points, les corrections sont donc les bienvenues.



Discutons encore une fois du fonctionnement du système de suspension magnétique du rotor. Si nous prenons deux aimants, l'isoligne potentielle ressemble à ceci, en fonction de la distance entre les aimants:



Donc, nous avons mis deux aimants fixes sur un stator. L'aimant placé sur l'axe du rotor ne voudra pas se déplacer latéralement, car l'isoligne potentielle a un certain point minimum local. Au lieu de cela, il voudrait sortir le long de l'axe du rotor. On fait deux de ces systèmes et au final, l'axe du rotor est stable radialement, mais instable latéralement. Nous corrigeons cela en inclinant le rotor contre une paroi en verre et le tour est joué - nous avons un roulement à faible friction.

Mais la paroi de verre est un peu ... pas esthétique, non? Il est logique que nous voulions suspendre complètement le rotor dans l'air, sans béquilles mécaniques comme celle-ci. Et évidemment, Dmitry a également été bombardé de la même question, c'est pourquoi il a dû noter dans la description que c'était impossible. Et je parie que Dmitry n'est pas le seul à s'en lasser.

Voyons cela, je cite:

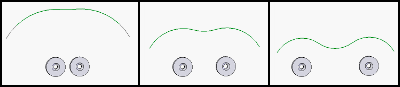
Que se passerait-il si les aimants de base étaient espacés et orientés comme dans ce dessin? Cela lui donnerait-il de la stabilité dans le plan axial et éliminerait-il l'exigence du miroir?

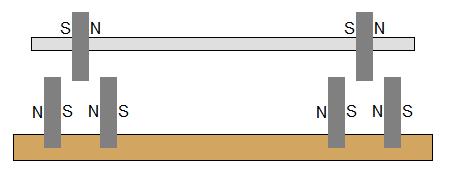
Ou ici , je cite:

Sur un moteur Mendocino, pourquoi un côté flotte-t-il librement tandis que l'autre a une pointe contre un mur? Je sais que la question peut sembler triviale, mais j'ai trouvé l'idée pourquoi ne pas utiliser les mêmes aimants utilisés pour léviter comme contre-force des deux côtés de l'arbre? J'ai joint un jpg très approximatif de ce que je veux dire. les aimants verts à l'extrémité des arbres sont ce à quoi je me réfère. y a-t-il une théorie ou une loi qui l'empêche?

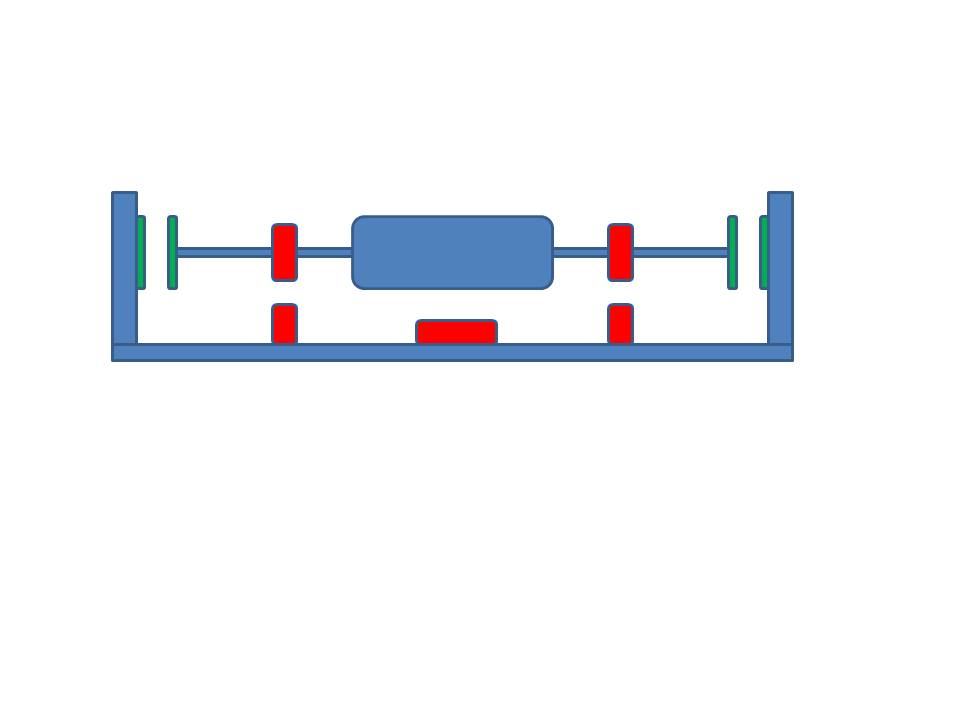
Nous pouvons voir que beaucoup de gens dans le monde veulent se débarrasser de cette partie mécanique inconvenante. Je n'accordais pas beaucoup d'attention à mes études, donc il n'était pas du tout évident pour moi pourquoi un système de suspension magnétique complètement stable était irréalisable. Un jour, à l'heure du déjeuner, j'ai posé cette question à mon superviseur, un scientifique de renommée mondiale (en mathématiques appliquées, pas en physique): «Pourquoi est-ce impossible?». Et vous savez quoi, il ne le savait pas non plus!

Les forums affichés ci-dessus n'ont pas non plus fourni de réponse appropriée à cette question. Dans le meilleur des cas, quelqu'un a fait référence à quelque chose appelé le théorème d'Earnshaw , qui ne se prête pas à la compréhension à première vue. Il stipule que: une collection de charges ponctuelles ne peut pas être maintenue dans une configuration d'équilibre stationnaire stable uniquement par l'interaction électrostatique des charges. L'avez-vous compris? Certainement pas. Disons que je peux accepter le fait que nous parlons de charges et non d'aimants. Alors quoi?

Première illustration

Quand je ne peux pas enrouler ma tête autour de quelque chose, j'ai tendance à le dessiner. Illustrons cela en 2D, pour plus de simplicité. Imaginez quatre charges fixes, placées dans un motif carré, plus une charge gratuite au centre. Comme ça:



La charge gratuite n'est-elle donc pas en équilibre? Peu importe où il se déplace, il se rapproche de l'une des charges fixes, ce qui augmente la force de poussée! Essayons de dessiner une carte de l'énergie potentielle d'une charge gratuite. J'ai manqué beaucoup de cours de physique à l'école, donc mon référentiel de connaissances est Wikipédia. Donc, si vous n'avez qu'une seule charge fixe, cela crée un potentiel électrostatique dans le champ qui l'entoure:

L'équation du potentiel électrostatique (ou potentiel de Coulomb) d'une charge ponctuelle dans le vide:

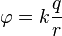
Dans toutes mes expériences de pensée, tous les coefficients sont soit 0 soit 1. Ainsi, la charge q est 1, et l'inconnu k est également 1. Cela signifie qu'une charge fixe crée une énergie potentielle mesurée comme 1 / r, où r est la distance à la charge.

Dans notre cas, l'énergie potentielle de la charge libre dans le champ de la charge fixe est également égale à 1 / r. (pour être juste, l'énergie est égale à k * q1 * q2 / r, mais nous choisissons les coefficients pour faciliter les calculs). Pour plusieurs charges, nous additionnons simplement tous les potentiels.

Tirons une carte de l'énergie potentielle de notre charge gratuite. J'utilise la sauge pour cela:

var('x,y') def unit_potential(a,b,x,y): return 1/(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True) 

Voici notre carte. Les points blancs (perforés) sont l'endroit où l'énergie potentielle devient infinie:



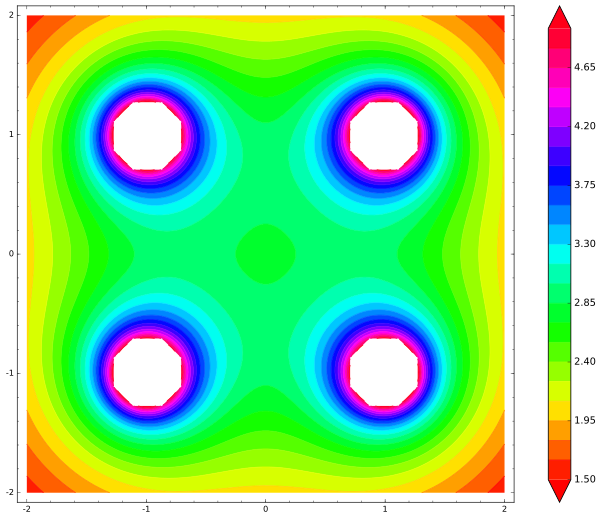
Nous voyons clairement le minimum local d'énergie au centre. Partout où la charge centrale veut se déplacer, l'énergie augmentera, donc de petites perturbations la forceront à revenir au centre - le point d'équilibre stable. Earnshaw avait-il tort alors? Non, il ne l'était pas, j'ai juste dessiné l'illustration de manière incorrecte. Et c'est une erreur courante chez les personnes qui posent cette question. Arrêtez-vous quelques minutes maintenant et devinez: qu'est-ce que j'ai raté?

En fait, dans ce cas, l'erreur était que dans un espace à deux dimensions, la charge fixe crée une énergie potentielle mesurée comme -ln r, où r est la distance à la charge, et non 1 / r. Prends ma parole pour le moment et laisse-moi corriger l'équation sans trop expliquer. Le code correct ressemble à ceci:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True) 

Et voici la carte qu'elle produit:



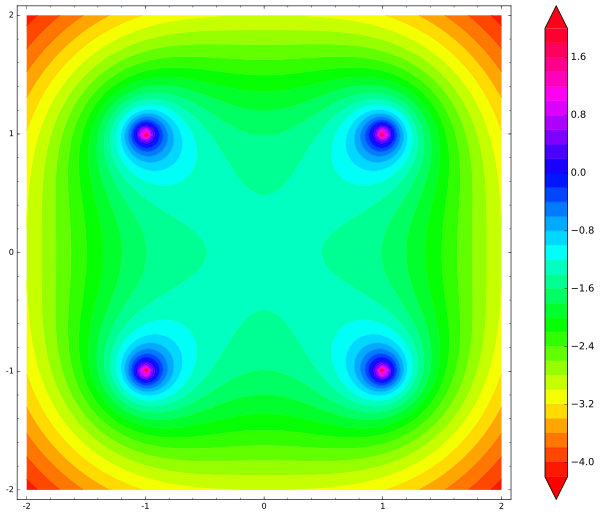
Notez qu'il n'y a de minimum local nulle part. Le centre est le point de selle, ou le point d'équilibre instable . Dès que la charge gratuite s'éloigne même d'un micron du centre, elle s'envolera inévitablement du système, accélérant en cours de route,

Attendez une seconde, qu'est-ce que vous venez de faire à l'équation?

Au début, quand j'ai réalisé que mes calculs étaient totalement contraires au théorème d'Earnshaw, j'ai réalisé que j'avais fait une erreur quelque part. Il est plus facile de retracer mes pas depuis le tout début. Je pris une profonde inspiration et allai lire sur les équations de Maxwell . Encore une fois, je n'étais pas trop bon à l'école: pas dans les notes (c'était excellent), mais dans la quantité de connaissances que j'en retirais. Par exemple, j'ai immédiatement oublié les équations de Maxwell, car à l'université et au-delà, je n'avais pas à travailler avec elles.

Il s'avère qu'ils sont assez simples, surtout si nous parlons uniquement de lois électrostatiques! Il existe quatre équations de Maxwell, une pour chacune de ces lois:

• La loi de Gauss, nous en aurons besoin plus tard. En bref, c'est une loi de conservation: l'énergie ne peut pas être créée à partir de rien, ni détruite.
• La loi de Gauss pour les champs magnétiques, qui est essentiellement la même chose. Et nous n'entrons pas encore dans les champs magnétiques, car nous ne parlons que de particules chargées. Ignorez cette loi.
• La loi de Faraday: les aimants en mouvement créent un champ électrique. C'est intéressant, nous verrons cela plus tard.
• La loi Ampère: déplacer un champ électrique crée un champ magnétique. Inutile pour nos fins.

Ainsi, ces quatre lois lient deux vecteurs E et B, les champs électriques et magnétiques. Ces vecteurs sont des fonctions avec quatre arguments (x, y, z, t) et chacun des quatre arguments est juxtaposé à un vecteur tridimensionnel. Nous ne sommes pas très intéressés par les champs magnétiques, alors regardons les champs électriques, ou E (x, y, z, t). N'oubliez pas que nous sommes dans le domaine électrostatique, donc E est constant dans le temps. Vous pouvez imaginer ce vecteur comme une rivière, où à chaque point, nous disons où et à quelle vitesse l'eau va.

La loi de Faraday stipule qu'un champ E à constante de temps (nous parlons ici d'électrostatique) n'a pas de boucle .

Comment le potentiel électrostatique est-il connecté aux champs électriques? Simple: si le champ E est sans boucle (comme c'est le cas ici), alors nous pouvons créer u d'une manière qui (pour revenir à l'exemple de la rivière), recouverte d'une couche d'eau de 1 mètre (à toutes les hauteurs! ) et «libérant: cela, la vitesse et la direction du débit d'eau créeraient le champ E. Ou, en termes mathématiques, il est possible de trouver une fonction scalaire u, dont le gradient est égal au champ E.

La loi de Gauss stipule: prenez un petit quartier. Si nous ne l'avons pas délibérément accusé, alors la quantité «d'eau» qui coule dans le quartier est égale à la quantité qui s'écoule. Si nous voulons paraître intelligents, la divergence du champ E est nulle.

Rappelez-vous: le champ E est une dérivée de la fonction scalaire u. Si sa divergence est nulle, cela signifie que le laplacien de u est nul. Le laplacien est un mot intelligent pour désigner la «courbure» de la fonction. Si nous parlons de fonctions à une variable, le laplacien est simplement la dérivée seconde. Dans les fonctions à deux variables, le laplacien est la somme de deux dérivées. S'il est égal à zéro, la courbure dans une direction doit être annulée par la courbure dans l'autre direction. Signification, les chips peuvent exister:



Mais la fonction zéro-laplacien n'a pas de minimums locaux (ou maximums), ce qui signifie que les chips sont autorisés, mais les collines ne le sont pas:



Imaginez plonger un cercle (incurvé) de fil dans de l'eau savonneuse. Le film de savon forme alors une surface zéro laplacienne:



Ce sera la soi-disant «surface minimale». Le film de savon essaie d'être aussi petit que possible, il est donc logique que s'il avait un certain maximum local, nous aurions un film plus petit en le lissant, donc il n'y en a pas. Ainsi, le potentiel électrostatique est une sorte de surface minimale qui n'a pas de maximum local (tant que nous n'y avons pas délibérément placé de charges).

La fonction 1 / r a un laplacien nul en trois dimensions, mais pas en deux! Si nous voulons dessiner des exemples à deux dimensions, nous aurions besoin de résoudre un problème de Dirichlet - pour la 2D, c'est -ln r.

L'utilisation de la formule des carrés inverses dans un espace à 1 ou 2 dimensions correspond à restreindre le mouvement des charges le long des axes restants d'une autre manière. Dans ce cas, il est évident qu'il est possible de faire une configuration stable - il suffit de prendre un tube en carton, de le mettre verticalement et de déposer son aimant. Ensuite, il est possible d'y placer un aimant de plus qui sera en équilibre - horizontalement, il est limité par le tube (c'est-à-dire qu'il est dans un espace unidimensionnel), et sur une force de gravité verticale et la répulsion d'un aimant sont contrebalancées. Le théorème d'Earnshaw doit soit être appliqué avec la loi des carrés inverses - mais en 3D, ou dans l'espace de n'importe quelle dimension, mais avec le potentiel correspondant. "Correspondant" signifie celui obtenu à partir des équations de Maxwell.

Le théorème d'Earnshaw et ses conséquences

Donc, revenons à notre exemple avec une particule chargée libre. Le potentiel d'un champ électrostatique n'a pas de minimum local et, par conséquent, l'énergie potentielle de la particule n'a pas de minimum local. Une particule ne peut donc pas atteindre un équilibre stable dans un champ statique. Félicitations, nous venons de prouver le théorème d'Earnshaw. Mais qu'en est-il des systèmes plus compliqués? Comment y appliquer le théorème?

Voici un autre exemple qui, selon mon patron, aurait dû réfuter le théorème d'Earnshaw. Fixons deux charges et créons un corps en mouvement composé d'un bâton non extensible et léger avec des charges aux deux extrémités:



Intuitivement, si nous déplaçons légèrement le bâton vers la gauche ou la droite, alors l'une des extrémités se rapprocherait des charges fixes, ce qui le repousserait et ramènerait le bâton à sa position d'origine. Alors quel est le problème? Tirons une carte du potentiel électrostatique de deux charges fixes:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True) 

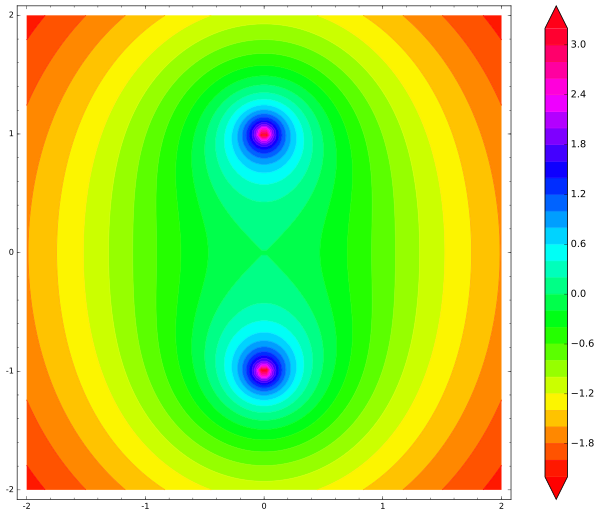
Comment illustrons-nous l'énergie potentielle de notre bâton? Le bâton a trois degrés de liberté (deux pour le mouvement et un pour la rotation), le graphique serait donc en quatre dimensions. Ignorons la rotation pour l'instant et ne laissons que le bâton se déplacer latéralement. Nous fixons un point sur un bâton (par exemple, son centre) et dessinons la carte de l'énergie potentielle du bâton pour son centre. Dans ce cas, l'énergie potentielle totale du bâton est la somme des énergies potentielles de ses charges aux deux extrémités:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y) def energy(x,y): return system_potential(x+2,y)+system_potential(x-2,y) contour_plot(energy(x,y), (x, -3, 3), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True) 

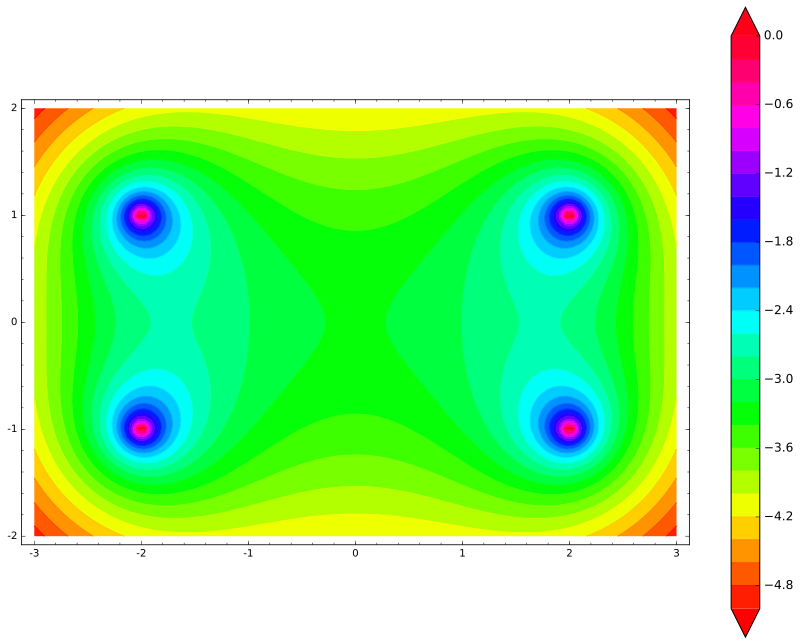
Ainsi, l'énergie du bâton a quatre pics (chaque extrémité peut toucher chacune des deux charges). Comme prévu, le bâton ne se déplacerait pas horizontalement - à la place, il se déplacerait verticalement!

C'est logique, car comment avons-nous obtenu l'énergie? Nous avons additionné les énergies potentielles de chaque charge. Nous savons que l'énergie potentielle de chaque charge est une fonction zéro-laplacienne. Sa somme a donc également un laplacien nul. Par conséquent, l'énergie potentielle de tout corps chargé (pas seulement notre bâton!) Ne peut pas avoir de minimum dans un champ électrique statique!

Conclusion

Des images intuitives de champs magnétiques et électriques de personnes qui ne travaillent pas étroitement en physique peuvent être trompeuses. Notre cerveau nous trompe en faisant des images de minimums d'énergie. Malheureusement, ce n'est pas le cas, et créer un moteur Mendocino sans support mécanique est très difficile, voire impossible.

Quelles sont les failles à exploiter? Le théorème d'Earnshaw (si nous l'appliquons aux aimants) ne s'applique qu'aux systèmes d' aimants statiques fixes .

1. Nous pouvons créer un champ magnétique dynamique.
2. Le diamagnétisme et les supraconducteurs ne relèvent pas non plus du théorème d'Earnshaw.
3. Les corps en mouvement (et en particulier en rotation) n'y sont pas du tout discutés, le lévitron étant l'exemple le plus célèbre.

Non, ce n'est pas sans espoir. Bien sûr, utiliser l'une de ces failles tuerait l'esthétique d'un moteur Mendocino, mais la magie d'une chose en métal à lévitation libre l'emporterait sur tout cela!

Dernière note: c'est le théorème d'Earnshaw qui a prouvé la non-existence de la matière solide, réfutant ainsi le modèle accepté d'un atome, qui a conduit au modèle atomique «planétaire».