Lorsque vous jouez selon les règles standard de Gomoku, les Noirs n'ont pas besoin de plus de
35 coups pour gagner. L'article présente à votre attention une stratégie gagnante complète et l'algorithme correspondant du jeu.
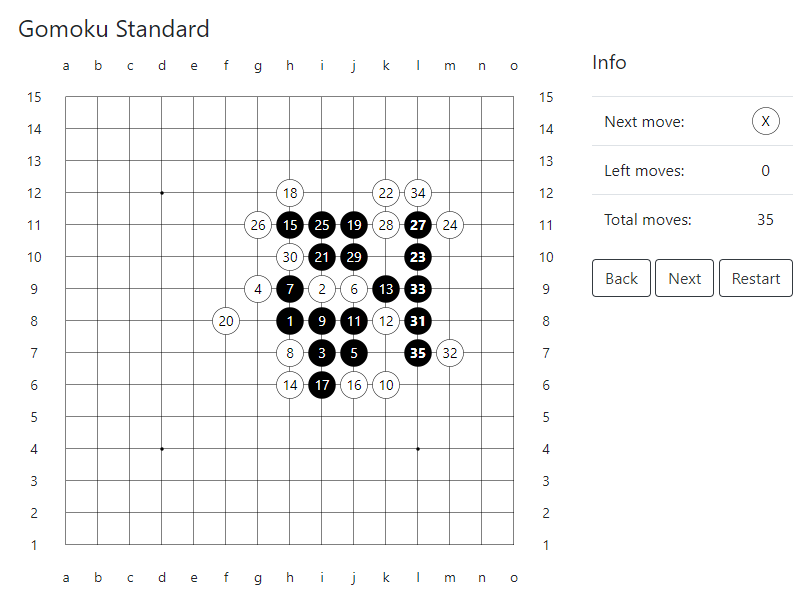
Démonstration de la solution complète -
ici - vous pouvez jouer et trouver les options les plus longues. Le programme gagne toujours et ne dépense pas plus de 35 coups. Le code source de l'application, la solution elle-même et des exemples de parties à la fin de l'article.
Je ne m'attarderai pas sur les règles et tactiques du jeu. Le sujet a été discuté en détail sur habr
ici , ainsi que sur les algorithmes de décision
ici et
ici .
Petite digression
Avant l'ère des smartphones, le tic-tac-toe «cinq de suite» (Gomoku, Renju) était l'un des tueurs les plus populaires de l'époque lors des cours scolaires. Envisager des combinaisons était plus intéressant que le développement de l'économie nationale d'Afrique du Nord ou la classification des fleurs de trèfle.
À l'automne 1985, les filles de notre 10e année ont été prises dans un cours de mathématiques. Nous, les six autres enfants, étions les plus susceptibles d'avoir une communication informelle avec un professeur de mathématiques sur des sujets abstraits. L'enseignant est entré dans la salle de classe en silence, a distribué des brochures à tout le monde dans une boîte et a commencé à écrire les noms des personnes présentes sur le tableau noir. Nous étions déprimés, un travail indépendant ou une enquête éclair était prévu. Mais la liste au tableau s'est transformée en classement et on nous a annoncé les règles du championnat. Chacun avec chaque série de cinq parties. Prix au gagnant - cinq au magazine. Selon les résultats du tournoi, j'ai eu la chance de gagner, mais le jeu ne s'est pas arrêté là. Le professeur a promis de mettre cinq à tous les gars si le vainqueur remporte les cinq matchs consécutifs de la série. Le droit du premier coup est donné au vainqueur. Contrairement à l'affirmation de notre professeur que dans une telle condition, avec le bon jeu, vous pouvez gagner 10, 100, ou n'importe quel nombre de matchs d'affilée, la victoire m'a semblé une chance incroyable.
Neuf ans plus tard, en 1994, le Dr Lewis Victor Allis a présenté des preuves de cette hypothèse dans un article de
Go-Moku et Threat-Space Search . L'auteur n'a pas publié sa stratégie gagnante, ce qui lui permet de vérifier la preuve. Cependant, dans son livre de 1996
Searching for Solutions in Games and Artificial Intelligence , une description générale des algorithmes a été fournie. En conclusion, nous mentionnons séparément la procédure de vérification de l'exhaustivité d'une stratégie gagnante, qui repose sur la justesse de la mise en œuvre de l'algorithme de recherche pour la "séquence de menaces" et l'analyse des options de contre-jeu de l'adversaire.
Les exemples de solutions donnés dans l'article et le livre avec les «bons coups» des adversaires, qui font partie d'une stratégie gagnante, démontrent la faiblesse de l'algorithme utilisé.

Par exemple, dans la figure, la solution du programme pour les règles Gomoku standard. Si les Noirs répondent avec j10 puis j8 en réponse au 10ème coup g9 des Blancs, alors le jeu se termine par 29 coups au lieu de 45. Ensuite, le programme deux fois "n'a pas remarqué" la combinaison de la "séquence de menaces" des Noirs en 17 coups après le 16 et après 26- Le mouvement de White. Et au final, si Blanc effectue le 36ème coup f12 au lieu de j12, il tiendra au moins jusqu'au 49ème coup. Pour être honnête, il faut dire que dans cet exemple, tous les mouvements des Noirs ne laissent aucune chance aux Blancs de terminer le match en sa faveur.
Sur Internet, j'ai trouvé plusieurs références à des travaux similaires à la recherche d'une stratégie gagnante. La question de l'optimalité des solutions trouvées reste en suspens. Quel est le nombre minimum de coups que les Noirs doivent gagner?
Ainsi, ayant un peu de temps libre, des ressources informatiques modernes et rendant hommage aux passe-temps des enfants 33 ans après le championnat mémorable de l'école, il s'est fixé pour tâche de trouver la stratégie gagnante optimale pour Black in Gomoku.
Numérisez la position au tableau
L'enregistrement d'une partie est assez primitif. Il n'y a que 225 cellules sur le terrain. Par conséquent, chaque cellule est codée sur 1 octet. Pour enregistrer un lot de 35 mouvements, seulement 35 octets sont nécessaires. Mais un tel enregistrement est mal adapté à l'évaluation de la position pour deux raisons: la même position peut être obtenue dans une séquence différente de mouvements et les positions symétriques ne sont pas prises en compte.
Atteindre l'objectif du jeu - construire cinq pierres d'affilée - peut être réalisé dans l'une des quatre directions: verticale, horizontale et deux diagonales. Ainsi, nous pouvons représenter n'importe quelle position comme un ensemble de lignes. Lignes horizontales et verticales d'une longueur de 15 cellules et lignes diagonales d'une longueur de 1 à 15 cellules. Chaque mouvement change la valeur de 4 lignes dans différentes directions à la fois.
L'évaluation d'une position consiste à déterminer tous les chiffres significatifs pour chaque ligne. Pour simplifier, nous décrivons chaque cellule de la ligne avec 2 bits. Le premier bit est plein lorsqu'une pierre blanche est installée, le deuxième bit est une pierre noire. Chaque ligne ne contient pas plus de 15 cellules et est codée en un entier 32 bits. Ainsi, la recherche de formes sur une ligne se réduit à comparer la valeur numérique de la ligne à travers une fenêtre coulissante avec le motif binaire de la forme.

Dans l'exemple illustré sur la figure, la position est décrite par 26 lignes. En conséquence, il est codé avec 104 octets, tandis qu'un enregistrement de lot régulier ne nécessite que 17 octets.
Il est facile de deviner que toutes les symétries - tours et images miroir - sont obtenues en changeant simplement le nombre (mélange) et la direction des lignes. Pour identifier une position et rechercher rapidement des collections, ce principe implémente une fonction de hachage 32 bits qui donne des valeurs différentes uniquement pour les positions asymétriques.
L'utilisation de symétries réduit considérablement le nombre de positions considérées. Par exemple, le nombre d'options pour le deuxième mouvement est réduit de 224 à 35.
Lors de la recherche de solutions et de combinaisons (cela sera discuté ci-dessous), les positions calculées constituent les sommets du graphe multicouche. Les sommets sont regroupés en couches en fonction du nombre de cellules remplies. Les mouvements constituent les bords du graphique, reliant les sommets des couches adjacentes. Lorsque les déplacements infructueux sont rejetés pendant la recherche, les bords sont supprimés et certains des sommets perdent leur connectivité avec la branche principale. Par conséquent, après les étapes de calcul, la récupération de place (ou la reconstruction du graphique à partir du haut) est effectuée.
Au cours du processus de développement, plusieurs algorithmes de codage ont été envisagés, mais celui décrit ci-dessus a montré le taux d'estimation de position le plus élevé.
Évaluer la position
Un facteur important pour évaluer une position est l'importance des adversaires pour construire les pièces importantes.
Cinq - si une telle pièce est trouvée sur le plateau, la partie est terminée. Pour les règles standard, pas de six, sept, etc., donnez un prix à Gomoku. Par conséquent, les cinq, comme d'ailleurs toutes les autres figures, nécessitent l'absence de leurs pierres sur les cellules voisines en ligne.
 Les quatre ouverts
Les quatre ouverts - la longueur de 6 cellules, les quatre du milieu sont occupés par des pierres de la même couleur, les externes sont nécessairement vides. Eh bien, comme pour cinq, leurs pierres sont absentes dans les cellules voisines. Un chiffre très fort signifie gagner même sur le coup de quelqu'un d'autre.
 Quatre
Quatre - la longueur de 5 cellules, une (n'importe laquelle) des cinq cellules est libre. Donne une victoire tout seul. Cela crée une menace et oblige l'adversaire à faire un mouvement dans une cellule libre s'il n'a pas ses quatre. Donne 5 points dans le classement de la position pendant la défense.

 Un triple ouvert
Un triple ouvert - la longueur de 6 ou 7 cellules, les cellules les plus externes sont nécessairement libres. Pour 6 cellules, trois des quatre centrales sont occupées par des pierres de même couleur, une libre. Pour 7 cellules - trois moyennes sont occupées par des pierres de la même couleur. Une pièce à son tour devient un quatre ouvert si l'adversaire n'en a pas quatre ou trois ouverts. Sur le coup de quelqu'un d'autre, cela crée une menace et force l'adversaire à fermer les trois ou à mettre ses quatre en réponse. Le triple de 6e cellule a 1 mouvement de relance et 3 mouvements de fermeture. Le triple de 7e cellule a 2 mouvements de relance et seulement 2 mouvements de fermeture. Donne de 2 à 4 points dans la cote de position.


 Un triple
Un triple , ou un triple fermé, est une longueur de 5 cellules, dont trois sont occupées par des pierres de la même couleur. Les trois à son tour peuvent être transformés en quatre et sont utilisés en attaque et en défense, créant une menace plus qu'un trois ouvert de l'adversaire. Donne 1 point en note de position.


 Un diable ouvert
Un diable ouvert (en perspective) - de 6 à 7 cellules de long. Lors d'une attaque, il est converti en trois ouverts. Donne 1 ou 2 points dans la cote de position.


 Un plug
Un plug est en même temps deux menaces ou plus qui ne peuvent pas être fermées en une seule fois. Il y a des fourches 3x3 (deux triples ouverts), des fourches 3x4 (trois et quatre ouvertes) et des fourches 4x4 (deux fours ouverts). créant de grandes menaces - une séquence de quatre pour une fourche 3x3.



 Combinaison
Combinaison - une séquence continue de menaces et de défenses contre des menaces plus importantes de l'adversaire, conduisant à un résultat positif pour le joueur. Les combinaisons attaquent (ou gagnent) et défensives.
La combinaison d'attaque ou de victoire est réussie si, sur n'importe quel mouvement défensif ou d'attaque de l'adversaire, des mouvements de réponse ont été trouvés conduisant à une victoire. La combinaison d'attaque se termine par l'installation d'un bouchon, que l'adversaire ne peut pas fermer.
La combinaison défensive, au contraire, réussit lorsque l'adversaire cesse de créer des menaces, ou lorsque la limite de mouvements pour le calcul est dépassée. Une combinaison défensive consiste en des mouvements défensifs ou en créant une plus grande menace pour l'adversaire.
Lors de l'évaluation d'une position, une recherche d'une combinaison gagnante est effectuée. En cas de succès, nous avons gagné. Sinon, s'il n'y a pas de menaces de la part de l'adversaire, l'État est neutre. S'il y a des menaces de l'adversaire, nous recherchons une combinaison défensive. En cas de succès, l'État est neutre; s'il échoue, nous perdons.
Étant donné que le nombre d'options d'attaques et de mouvements de représailles forcés est assez limité, il est permis de rechercher des combinaisons à une profondeur suffisamment grande. Lors de la construction initiale de la stratégie optimale, la profondeur autorisée de la recherche de combinaisons a été établie en 25 coups. Lors du recalcul de la solution pour implémenter l'algorithme d'estimation de position en javascript, la profondeur de recherche autorisée a été réduite à 17 mouvements.
Lors du calcul de la stratégie optimale, la profondeur de recherche de la combinaison gagnante ci-dessus a en outre été limitée par le nombre maximum de coups cible.
Nous recherchons une solution
Nous avons donc évalué la position donnée comme neutre et choisi le prochain coup. Notre comportement dans ce cas dépend de notre position d'attaque ou de défense. Pour le côté attaquant, la solution complète sera une séquence de mouvements dans laquelle pour tout mouvement de retour de l'adversaire, la position est évaluée comme gagnante (une combinaison gagnante est trouvée) ou contient le prochain coup propre dans la solution. Il est à noter que pour calculer la stratégie optimale, le côté attaquant est toujours noir, le côté défenseur est blanc.
L'attaquant n'a besoin de trouver qu'un seul coup, menant à la victoire la plus rapide. Dans les conditions de manque de ressources, l'attaquant limite artificiellement le nombre d'options de contournement, j'étudie tout d'abord les mouvements menant à la position avec le score le plus élevé. Une fois toutes les solutions trouvées, dans le sens des plus longues d'entre elles, l'attaquant élargit la gamme d'options, explorant des positions moins notées afin de réduire la longueur de la solution.
Il suffit que le camp en défense trouve un seul coup qui ne mène pas à la victoire de l'adversaire dans la limite de coups donnée. Toutes les cellules libres peuvent être utilisées pour le dénombrement.
Pour réduire le nombre de coups à trier, nous utilisons l'algorithme «skip». Nous sautons le mouvement défensif et recherchons une combinaison d'attaque gagnante. En cas de succès, les mouvements de défense possibles peuvent être limités aux mouvements qui affectent le succès de la combinaison trouvée. En moyenne, à chaque étape, cela vous permet de réduire la zone de recherche de 4 à 6 fois. Veuillez noter que parmi les mouvements ignorés, il peut y avoir des branches plus longues de la solution. Par conséquent, pour rechercher des solutions optimales, l'algorithme de «saut» n'est utilisé que dans la recherche initiale.
Nous calculons la stratégie
Tous les composants sont prêts, nous mettons la première pierre noire au centre du terrain, commençons la recherche d'une solution et ... Quelques heures plus tard, les ressources de mon ordinateur portable sont épuisées et je dois admettre la défaite "au combat, mais pas au combat".
En vérité, j'avais à portée de main une puissance de calcul avec cent cinquante cœurs Xeon et un téraoctet de RAM libre. Mais rappelez-vous qu'au milieu des années 90, Allis n'avait que 10 SUN SPARCstation 2 sur chacun des 128 Mo de RAM, avait des remords pour un comportement antisportif et avait décidé de limiter la quantité de RAM sur la machine java à 1 Go et alloué seulement 1 thread pour la tâche le processeur. Il pourrait en quelque sorte compenser mon GHz par rapport à son MHz. De plus, il s'est promis à la fin des travaux de transférer les algorithmes en javascript pour le navigateur.
Ainsi, la recherche de stratégies a dû commencer par la décision des premiers croquis. Une description détaillée des débuts du jeu Renju en russe peut être trouvée dans les célèbres livres de Sagar "From Debut to Middlegame" et Mikhail Kozhin et Alexander Nosovsky "Ringing of the Stones"
ici . Les livres ont déjà 20 ans, mais depuis lors, un peu de cette littérature a été publiée. La plus récente collection de Dmitry Epifanov «Tiger in a cage» de 2015, malheureusement, n'est pas disponible sous forme électronique.
La recherche de décisions d'ouverture optimales a été réalisée selon l'algorithme suivant. Lors de la première étape, un calcul préliminaire a été effectué sans limiter la longueur du lot. Ensuite, pour les solutions les plus longues, l'optimisation a été effectuée: remplacer les combinaisons trouvées par des solutions plus courtes pour les étapes finales et rechercher des branches de décision plus courtes pour tous les mouvements intermédiaires. L'optimisation a été effectuée jusqu'à ce que la limite cible soit atteinte pour toutes les branches de la solution. Ensuite, la limite cible a diminué et une tentative a été faite pour optimiser à une nouvelle valeur.


Il n'y a eu aucun problème avec le 3e début vertical de la figure 3. Le résultat a été un ensemble complet de solutions. Les positions les plus difficiles après le 4ème coup i8 et j10 en conséquence ont été résolues en 31 coups. Ensuite, une limite cible de 35 coups par partie a été fixée.


De la diagonale de la décision, il a traditionnellement choisi le 7e début. La position la plus difficile apparaît après le 4ème coup g9. Des solutions de longueur admissible ont été trouvées pour 6 mouvements g8 et g7.

Mais pour cette option, avec le 6ème coup sur j9, je n'ai pas réussi à trouver une solution plus courte que 33 coups. C'était presque un désastre. Par désespoir, j'ai essayé les solutions pour le 5ème mouvement alternatif, ainsi que tous les autres types d'ouvertures diagonales. Les débuts ont été résolus jusqu'à la fin, mais rien de plus court que 39 coups par partie n'a pu être trouvé.
Revenant aux débuts originaux de la 7e diagonale, il a refait l'algorithme pour générer des phrases pour les mouvements d'attaque. En conséquence, les mouvements menant à des positions avec un score de notation du troisième dix ont commencé de manière inattendue à donner un résultat et à réduire la longueur du chemin de la solution. La variabilité du calcul avec un tel montant est devenue assez importante. Avec une profondeur de solution de 12 mouvements, il y avait plus de 2 millions de positions (hors positions lors de la recherche de combinaisons). La suite reposait sur 1 Go de RAM alloué à la tâche. Ainsi, afin de vérifier la décision à la fourche finale, dans certains cas, il était nécessaire de décider séparément des positions à partir du 18e coup.
Après que le début de la 7e diagonale eut été décidé en 35 coups, on pouvait célébrer la victoire - la lutte pour le centre était gagnée. Il y avait encore une énorme quantité de travail de calcul de routine, des calculs de mouvements blancs «non optimaux» pour compléter la stratégie. Sur le volume total de la stratégie optimale, la réponse à de tels mouvements a donc été de 80%. Heureusement, ils ont été automatiquement résolus complètement sur le calcul préliminaire après le 2e déménagement, et tout ce volume a été ajouté à la stratégie optimale en quelques jours.
Ainsi, des solutions pour les 2 mouvements ont été trouvées. Nous plaçons la première pierre noire au centre du terrain, entamons la recherche d'une solution et n'avons même pas le temps de ressentir l'importance du moment - la position initiale a été résolue en 35 coups. Le graphique de la stratégie gagnante optimale est construit.
Nous vérifier
L'étape suivante consiste à vérifier la solution. Désactivez complètement l'intelligence de la partie défensive. Après chaque mouvement de Noir, Blanc va sur n'importe quelle case libre du plateau. La position obtenue après le coup de Blanc doit être trouvée dans le graphique de décision ou évaluée comme gagnante pour le nombre de coups ne dépassant pas la branche la plus longue dans la position de départ. Lors de l'évaluation de chaque position, nous vérifions la combinaison gagnante trouvée pour tous les mouvements admissibles de Blanc avant que Noir ne construise la pièce finale - cinq d'affilée.
La vérification a été effectuée plusieurs fois jusqu'à la fin. L'exécution finale sans erreur en mode monothread a pris 14 heures. Au cours de la vérification, des erreurs ont été trouvées et corrigées, résultant de différences dans la profondeur de la recherche de combinaisons, d'hypothèses de saut, de duplication de positions symétriques.
Répondez à la question - la décision en 35 mouvements est-elle vraiment la plus optimale? Selon mes recherches, pour certaines des branches les plus longues des débuts verticaux, il est possible de trouver des solutions plus optimales avec une longueur de 33 mouvements. Mais pour la diagonale après le 6e coup sur j9, beaucoup de temps a été consacré à la recherche d'une solution en 33 coups, la variation pour les Noirs s'est étendue à 50 coups à chaque pas et en vain. Il n'est pas possible de prouver rigoureusement l'absence de solution en 33 mouvements, le temps alloué au projet est arrivé à son terme et il a été décidé de s'arrêter à la limite cible de 35 mouvements.
Convertir de java en javascript
La publication d'une solution à un problème demande de la clarté.
Pour utiliser la solution directement dans le navigateur, il fallait:- Réduisez la profondeur de la recherche de combinaisons lors de l'évaluation des positions à 17 mouvements. Cela a conduit à une augmentation de 2 à 3 fois du nombre de mouvements calculés de la stratégie optimale.
- Convertissez le format du graphique de décision binaire en séquence JSON de mouvements. Ce format est plus pratique en javascript et visuel.
- Convertissez les classes java en modules javascript, à l'exception des procédures de prise de décision. Ici, dans l'interface Web, remplacez les appels rest-service par des fonctions locales.
Liste des classes d'application:- Board - gestion des parties sur le board, interface visuelle
- Sommet - sommet du graphique de décision, hérité de la position
- Bord - bord du graphique de décision, déplacer les positions de connexion
- Disposition - position, contient une collection de lignes
- Ligne - une ligne dans une direction donnée, contient une collection de formes
- Figure - une figure qui détermine le type et le début d'une figure sur une ligne
- Modèle - modèles de figures pour comparaison lors de la recherche
La solution complète au format JSON peut être téléchargée à partir du fichier gomoku.json .Sources dans le référentiel sur GitHub .Pour plus de clarté, je vais donner ci-dessous des exemples des jeux les plus longs obtenus dans la démonstration en cliquant sur Suivant.Débuts en diagonale:
 Débuts verticaux:
Débuts verticaux:
