Niveaux de difficulté de lecture
Introduction et règles du jeu
Il y a quelques années, j'ai acheté le jeu Dobble ( Dobble , le nom d'origine est «Spot It!»). C'est un jeu très simple, rapide et amusant, que je considère comme l'un des meilleurs jeux de société en général.
Il y a 55 cartes dans le jeu avec 8 symboles différents sur chacune. Voici à quoi ressemblent ces cartes:

Fig. 1. Un exemple de carte de jeu.
Sur chacune des deux cartes, un et un seul symbole correspond. Dans la figure ci-dessus, il s'agit d'un symbole de crayon:

Fig. 2. Correspondance des personnages sur les cartes.
Le joueur qui a vu le match pour la première fois effectue une action sur l'une des cartes, en fonction du tour de jeu. Par exemple, le prend à lui-même ou le lance à un adversaire.
Cela conduit souvent au fait que l'une des cartes pour lesquelles les joueurs recherchent des matchs est en train de changer. Pour cette raison, vous devez rechercher une nouvelle correspondance, qui peut être un symbole complètement différent:


Fig. 3, 4. La première carte est remplacée par une nouvelle. Maintenant, il y a une nouvelle coïncidence entre eux - le symbole du clown.
Comment font-ils?
À première vue, il semble incroyable que sur deux cartes exactement une coïncidence, ni plus, ni moins. Les questions se posent immédiatement - combien de personnages y a-t-il dans le jeu? Ils ne peuvent pas être trop peu nombreux (alors il y aura plus d'un match sur les cartes) ou trop (alors il ne peut y avoir aucun match sur les cartes).
De plus, il est évident que les symboles sont situés sur les cartes dans un ordre spécial, ce qui garantit la seule correspondance pour deux cartes.
Les compétences élémentaires de Google nous conduisent au site Web stackoverflow, ce qui explique pourquoi cela se produit: http://stackoverflow.com/questions/6240113/what-are-the-mathematical-computational-principles-behind-this-game
Le jeu utilise les principes de la géométrie finie . Bien qu'il y ait le mot «géométrie» dans cette phrase, ce concept se réfère plus à la combinatoire qu'à la géométrie. Il fonctionne avec un nombre fini de points qui peuvent être localisés, notamment, sous la forme d'un plan projectif .
Les cartes et les symboles du jeu sont des éléments du plan projectif du 7e ordre. Cela signifie que sur chaque carte il y a n + 1 symbole, et le nombre total de symboles uniques dans le jeu est n ^ 2 + n + 1 , c'est-à-dire 57 caractères.
Il existe des avions d'ordre inférieur et supérieur. Par exemple, il existe un avion du 5e ordre. Pour elle, 6 symboles sont affichés sur la carte, et le nombre total de symboles uniques dans le jeu est de 5 ^ 2 + 5 + 1 = 31. Le plan projectif de cette configuration est utilisé dans une version plus simple du jeu Doble appelée "Doble 1,2,3" .
La connexion entre les points et les lignes pour le plan projectif est établie à l' aide de la matrice d'incidence . Son apparence est présentée dans la section «Matrice d'incidence du jeu Dobble».
Géométrie finale pour les bébés
Bien plus tard qu'écrire l' article original, j'ai assisté à une conférence d' Alexei Savvateev , où il a parlé de la géométrie projective beaucoup plus courte et plus compréhensible. Mais comme je n'ai pas la force ou le désir de réécrire la moitié de l'article à cause de cela, je recommande simplement son livre "Mathematics for Humanities", si ma tentative par le sauvage d'expliquer le dispositif de la voiture sur les doigts serait incompréhensible ou ennuyeuse.
Tout d'abord, allez sur Wikipedia et lisez quelques articles. Le premier article décrit le concept de géométrie finie:
Une géométrie finie est tout système géométrique ayant un nombre fini de points . [1]
Jusqu'à présent, tout est simple. Si vous dessinez plusieurs points avec un stylo sur du papier, ils constitueront déjà une sorte de géométrie finie.
Une surprise en attend bien plus:
Par exemple, la géométrie euclidienne n'est pas finie, car la ligne euclidienne contient un nombre illimité de points, ou plutôt, contient exactement autant de points qu'il y a de nombres réels . [1]
Pour nous, cela signifie que la feuille de papier sur laquelle nos points sont tracés n'est pas un plan en termes de géométrie finie . Ce n'est qu'un porteur de points.
Il existe deux types de géométrie sur le plan: affine et projective . En géométrie affine, la notion habituelle de parallélisme des lignes est utilisée. [1]
Rappelez-vous ce que les axiomes décrivent la géométrie affine:
La géométrie affine sur un plan est un ensemble X non vide (dont les éléments sont appelés «points»), avec une collection non vide de L sous-ensembles de X (dont les éléments sont appelés «directs»), tels que:
- Pour deux points différents, une seule ligne contient les deux points.
- Pour une ligne ℓ et un point p n'appartenant pas à ℓ , il existe une et une seule ligne ℓ ′ contenant p telle que ℓ ∩ ℓ ′ = ∅.
- Il y a beaucoup de quatre points, dont aucun ne se trouve sur la même ligne. [1]
Ces axiomes nous permettent de comprendre à quoi ressemble le plan affine le plus simple en géométrie finie:
Le plan affine le plus simple ne contient que 4 points, et est appelé un plan affine de second ordre . Chaque paire de points définit une ligne unique, donc le plan indiqué contient 6 lignes. [1]
Pas très clair? C'est vrai. Si vous regardez de près la définition de la géométrie affine, vous pouvez voir qu'elle fonctionne avec les concepts de la théorie des ensembles (élément, ensemble, sous-ensemble).
Cela signifie que les lignes peuvent ne pas ressembler du tout aux lignes habituelles de la géométrie euclidienne.
En fait, ça l'est. Si vous regardez l'image du plan affine de second ordre, nous verrons l'image suivante:

Fig. 5. Plan athénien du second ordre. (Source ru.wikipedia.org )
Les points ressemblent ici à des points noirs ordinaires, mais les lignes droites sont des segments multicolores. Les lignes de même couleur sont considérées comme parallèles.
Comme vous pouvez le voir, les lignes ici ne sont pas de longueur infinie. En secret, je dirai qu'il n'y a aucun concept de longueur ici, et les lignes droites peuvent avoir n'importe quelle forme, comme nous le verrons bientôt.
Certes,% username% doute encore que l'image de ce plan satisfasse les axiomes de la géométrie affine. Vérifions:
- Nous prenons 2 points quelconques, par exemple, le coin supérieur gauche et le coin inférieur gauche.
Ces deux points ne contiennent qu'une seule ligne rouge à gauche.
La ligne rouge de droite ne contient aucun de ces points et les lignes restantes n'en contiennent qu'un seul. - Prenez la ligne droite rouge gauche et le point supérieur droit. De toute évidence, une seule ligne droite (rouge droite) est parallèle à la ligne rouge gauche, car elle passe par le point supérieur droit, mais ne passe par aucun des deux points gauches.
- La figure montre clairement que peu importe les 3 points que nous prenons, l'un d'eux se trouve sur une ligne différente de la ligne sur laquelle se trouvent les deux autres points.
Les deux lignes qui composent les diagonales d'un carré ne se coupent pas, car elles n'ont pas de points communs.
Si vous avez bien compris le contenu de l'image précédente, alors l'image est plus compliquée:
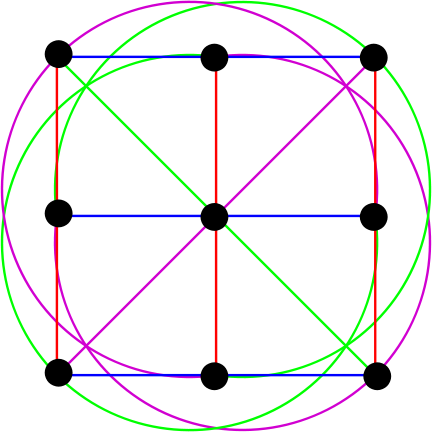
Fig. 6. Plan athénien du troisième ordre. (Source ru.wikipedia.org )
Ici, nous voyons 9 points et 12 lignes. Oui,% username%, ces ellipses sont en fait des lignes droites en termes de géométrie finie.
Les formes de la même couleur sont des lignes parallèles. Ils sont difficiles à remarquer, nous divisons donc l'image en plusieurs:
| Avion numéro 1 | Avion numéro 2 | Avion numéro 3 | Avion numéro 4 |
|---|
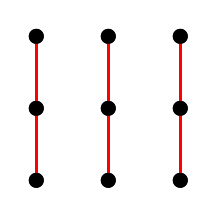 | 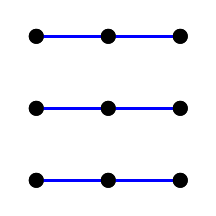 |  |  |
Fig. 7. Lignes droites parallèles du plan affine du troisième ordre.
Ici, la vérification de l'exécution des axiomes prendra un peu plus de temps:
- Nous prenons 2 points quelconques, par exemple, le centre supérieur et inférieur droit. À travers eux ne passe qu'une seule des lignes violettes.
- Prenez la ligne rouge gauche et le point inférieur droit. Comme pour un avion du second ordre, une seule ligne rouge droite passe par ce point, mais ne passe par aucun des trois points gauches.
- Ici, c'est un peu plus compliqué que dans le cas d'un avion du 2ème ordre. La déclaration de l'axiome indique que vous devez trouver au moins un ensemble (non vide) de quatre points, dans lequel aucun ne se trouve sur plus d'une ligne.
Évidemment, 12 ensembles avec trois points par lesquels passent les lignes de la figure ne remplissent pas cette condition. Mais il satisfait, par exemple, un ensemble de quatre points d'angle.
Dans un cas plus général, un plan affine fini d'ordre n a n ^ 2 points et n ^ 2 + n lignes; chaque ligne contient n points et chaque point appartient à n + 1 lignes. [1]
Une fois la géométrie affine terminée, nous passons au deuxième type de géométrie sur le plan - projectif.
Dans la géométrie projective, au contraire, deux lignes se coupent au seul point possible, et donc les lignes parallèles n'existent pas. [1]
La phrase précédente décrit le deuxième axiome de la géométrie projective. Le premier et le troisième sont les mêmes que dans l'Athénien.
Le troisième axiome nécessitant l'existence d'au moins quatre points, l'avion doit contenir au moins 7 points pour satisfaire aux conditions des deux premiers axiomes. Dans ce plus simple des plans projectifs, il y a aussi 7 lignes; chaque point appartient à trois lignes et chaque ligne contient trois points. Un tel plan projectif est souvent appelé «plan Fano» . [1]
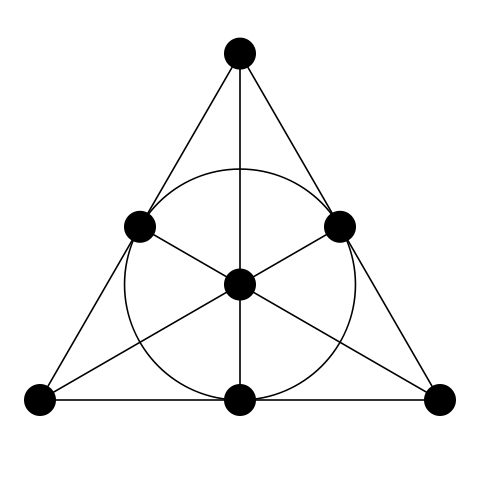
Fig. 8. Avion Fano. (Source en.wikipedia.org )
Sur cette figure, il est difficile de comprendre immédiatement les 7 lignes, voici donc une version poney du même avion:
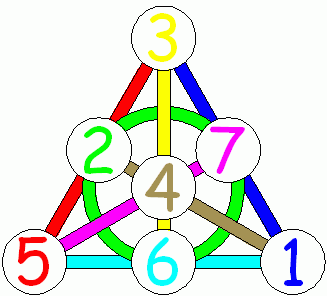
Fig. 9. Fano plane avec des lignes colorées. (Source mathpuzzle.com . Utilisé avec la permission d' Ed Pegg Jr. )
Ainsi, le plan de Fano est un plan projectif d'ordre 2 avec 7 points et 7 lignes.
Qu'est-ce que la carte a à voir avec ça?
Que se passera-t-il si nous reformulons 2 axiomes de géométrie finie , en remplaçant la «ligne» par le «symbole» et le «point» par la «carte»?
Le résultat est le suivant:
- Pour deux cartes différentes, il n'y a qu'un seul symbole, qui apparaît sur les deux cartes.
- Pour deux symboles différents, il n'y a qu'une seule carte qui contient ces deux symboles.
Maintenant, sur la base de ces connaissances, voyons à quoi ressemblerait Dobble dans le cas le plus simple. Il aurait 7 cartes et 7 caractères, chaque carte aurait 3 caractères (car 3 lignes se coupent en un point):
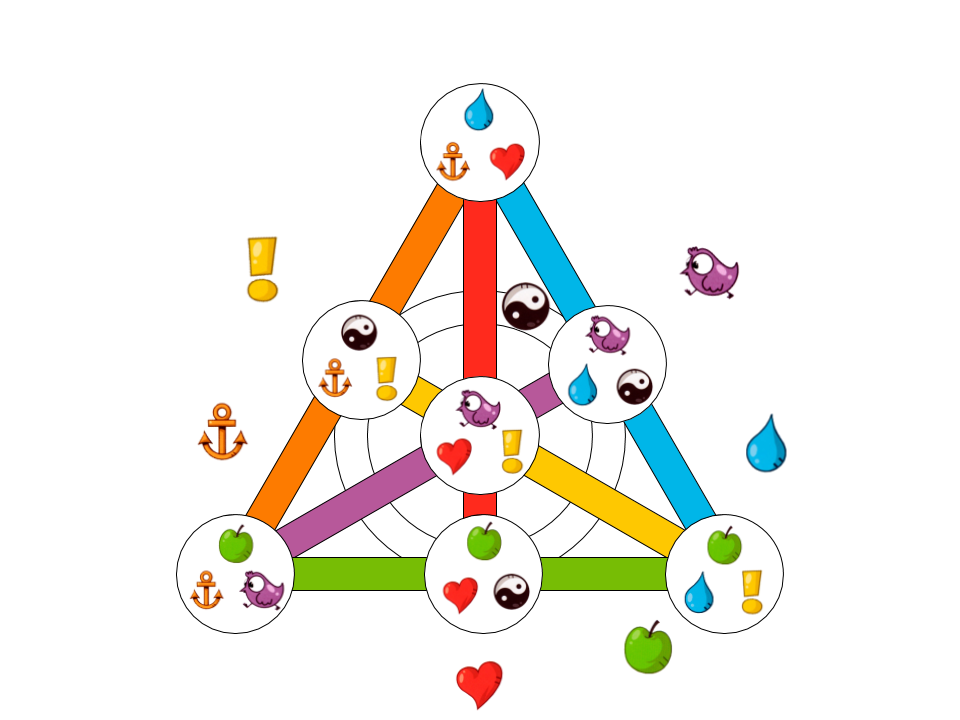
Fig. 10. Un exemple du plus petit jeu de cartes possible pour Dobble.
Les 7 caractères suivants sont utilisés ici:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
Peu importe les 2 cartes que nous prenons, elles auront un symbole commun, représenté à côté de la ligne sur laquelle se trouvent les deux cartes.
Par exemple, la carte dans le coin inférieur gauche et la carte au milieu du côté droit ont un symbole commun  . Il est affiché à côté de la ligne.
. Il est affiché à côté de la ligne.  .
.
Plans projectifs de petites commandes
Sur Wolfram, vous pouvez trouver une démonstration visuelle des plans projectifs de petites commandes: http://demonstrations.wolfram.com/ProjectivePlanesOfLowOrder/
Il est conçu comme un document au format CDF (Computable Document Format), pour lequel vous devez installer CDF Player .
Voici un exemple d'un plan projectif d'ordre 3:
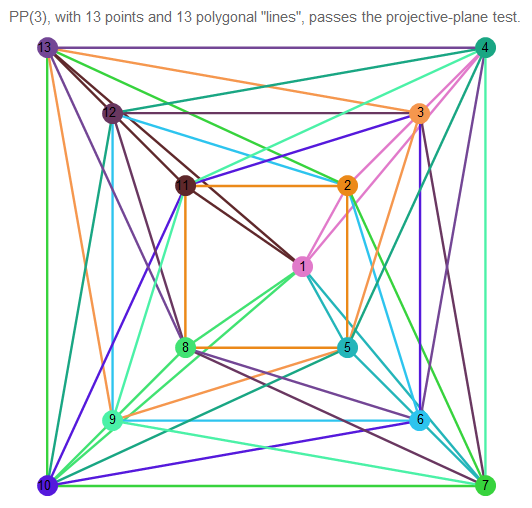
Fig. 11. Image du plan projectif de 3 ordres.
Il est difficile de comprendre ce qui se passe, alors prenez 2 lignes arbitraires:
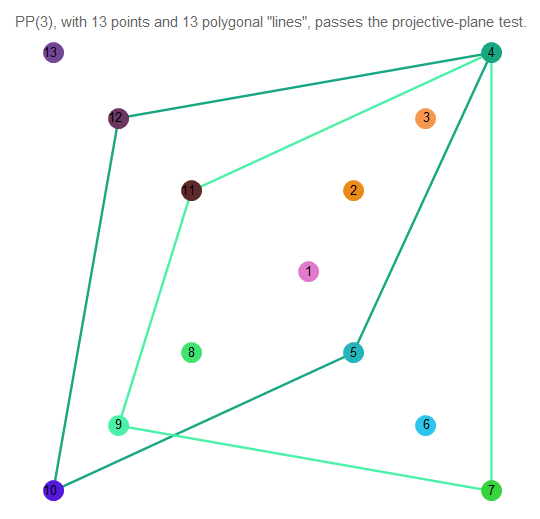
Fig. 12. L'intersection de deux lignes du plan projectif du 3ème ordre.
Comme nous le voyons, ils se coupent exactement en un point. Les lignes elles-mêmes contiennent 4 points.
Pour vous assurer que 4 lignes passent par chaque point, vous devez basculer les paires de lignes affichées dans un document interactif et vous concentrer sur un point.
Les plans projectifs d'ordre supérieur sont représentés dans les figures ci-dessous.
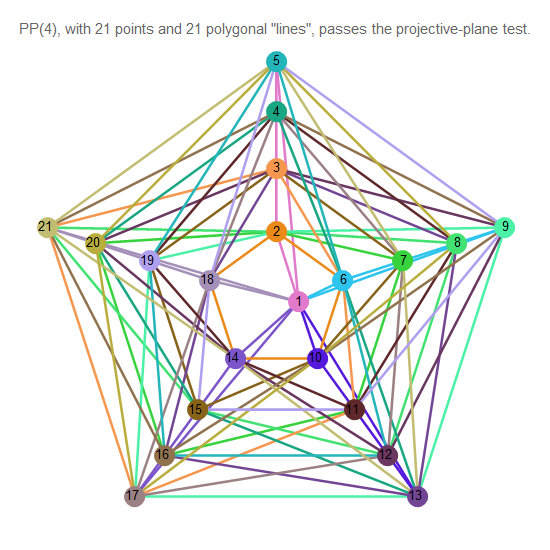
Fig. 13. Plan projectif d'ordre 4
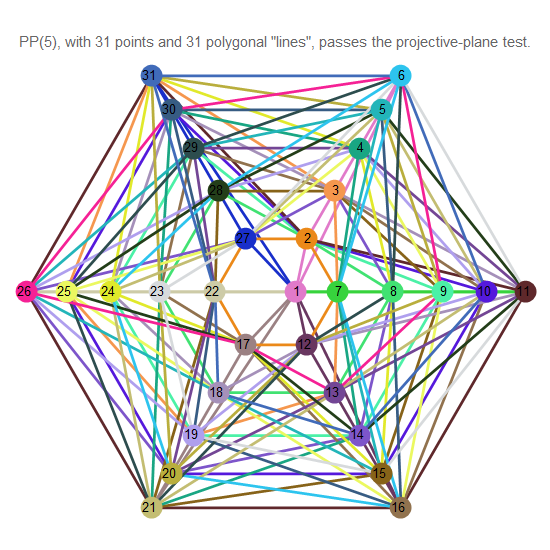
Fig. 14. Le plan projectif d'ordre 5

Fig. 15. Plan projectif d'ordre 7
Dans la séquence ci-dessus, il n'y a pas d'image pour le plan projectif du 6ème ordre. Ce n'est pas une erreur.
Bien que Wolfram génère une représentation graphique d'une telle structure, elle ne satisfait pas les axiomes de la géométrie projective et n'est pas un plan projectif.
On suppose, mais cela n'est pas encore prouvé, que l'ordre d'un plan fini est toujours une puissance première . [1]
Comment construire un plan projectif?
La représentation graphique du plan projectif semble intéressante et claire, mais comment trouver une telle combinaison de points pour qu'il possède les propriétés ci-dessus?
Le plus simple est de visiter des sites qui hébergent des données pré-calculées pour des plans projectifs de différents ordres.
Par exemple, pour le plan projectif d'ordre 7, vous pouvez visiter la page suivante: https://web.archive.org/web/20170619110638/https://www.uwyo.edu/moorhouse/pub/planes/pg27.txt
Une matrice de nombres y est présentée. Les lignes sont des cartes (points) en termes de Dobble. Les nombres dans les lignes sont les numéros de série des caractères (lignes), à partir de zéro, qui sont dessinés sur chaque carte (passez par ce point).
Vous pouvez également utiliser les services de packages mathématiques, tels que Matlab, pour construire la matrice d'incidence du plan projectif. [2] [3]
Matrices d'incidence
La matrice d'incidence est l'une des représentations graphiques qui indique les relations entre les éléments incidents du graphique (arête (arc) et sommet). Les colonnes de la matrice correspondent aux arêtes, les lignes aux sommets. Une valeur non nulle dans la cellule de la matrice indique la relation entre le sommet et le bord (leur incidence ). [2]
Un des exemples les plus simples de la matrice d'incidence peut être une matrice 2x1 pour un graphe non orienté de deux sommets reliés par une arête:

Fig. 16. Un graphique non orienté de deux sommets reliés par une arête et sa matrice d'incidence.
Un exemple plus complexe d'un graphique et de sa matrice d'incidence:
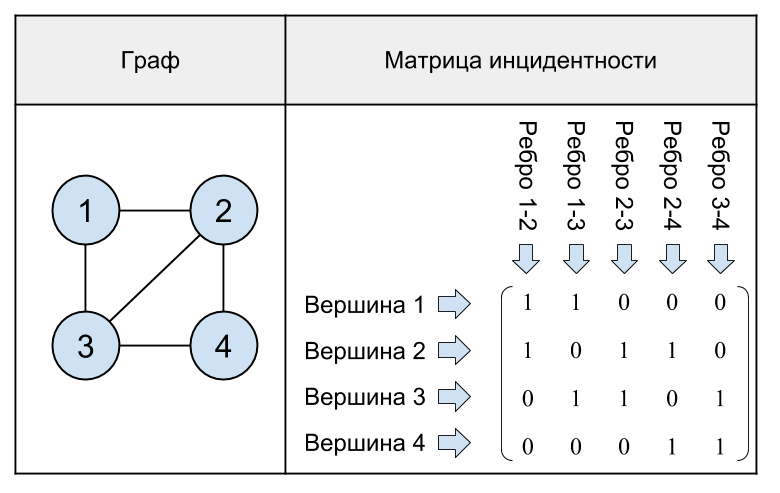
Fig. 17. Un graphique non orienté avec 4 sommets et sa matrice d'incidence.
Comme le montre le dernier exemple, dans la matrice d'incidence du graphique dans chaque colonne, il y a exactement deux unités, car une arête relie deux sommets.
Le plan projectif est un hypergraphe , car une ligne (arête) relie plusieurs points (sommets). Par conséquent, dans la matrice d'incidence du plan projectif, les unités dans chaque colonne se produisent n + 1 fois, où n est l'ordre du plan projectif.
Pour le plan Fano illustré à la Fig. 9, la matrice d'incidence sera la suivante:

Fig. 18. La matrice d'incidence du plan de Fano.
Pour simplifier la perception, les zéros ne sont pas affichés et les unités sont remplacées par le symbole X.
Dans cette représentation du plan projectif, le principe de dualité des points et des lignes est clairement visible - la ligne passe exactement par 3 points et, en même temps, le point appartient à exactement trois lignes.
Construire un plan projectif par force brute
Les connaissances actuelles sur les propriétés de la matrice d'incidence sont suffisantes pour la construire pour le plan projectif de tout ordre n. Pour ce faire, vous pouvez utiliser le pseudocode suivant:
n+1 , n+1 , ,
En suivant cet algorithme, nous obtenons une matrice symétrique pour le plan de Fano:

Fig. 19. La matrice d'incidence du plan de Fano construite par l'algorithme de pseudo-code.
Cette matrice ne correspond pas à la précédente. En fait, cela n'a pas d'importance.
La permutation de deux rangées quelconques de la matrice d'incidence équivaut à renuméroter les sommets du graphique.
La permutation de deux colonnes quelconques de la matrice d'incidence équivaut à renuméroter les bords du graphique (s'ils sont numérotés à l'avance).
Matrice des incidents pour Dobble
Pour le jeu Dobble dans la matrice d'incidence, les lignes sont responsables des cartes et les colonnes sont responsables des symboles qu'elles contiennent.
Ainsi, la permutation de deux colonnes quelconques de la matrice d'incidence équivaut à un changement dans la séquence de caractères sur la carte. Cependant, les symboles sur la carte ne sont pas classés, donc cette opération n'affecte pas l'apparence des cartes.
Le réarrangement de deux lignes signifie que sur toutes les cartes, deux symboles correspondants se remplacent.
La dernière opération change l'apparence des cartes, ce qui signifie que l'ensemble des personnages que nous voyons dans le jeu n'est qu'une des combinaisons possibles.
Le nombre de jeux de caractères pour une carte donnée est une combinaison de 57 éléments et 8 éléments sans répétition. Il est calculé par la formule 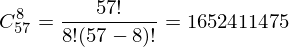
La matrice d'incidence de Dobble est présentée dans le tableau ci-dessous. Il est transposé, c'est-à-dire les lignes sont des symboles et les colonnes sont des cartes (l'image est cliquable). Habr ne vous permet pas d'insérer une image de la taille et de la qualité souhaitées, donc l'option pleine taille est un lien distinct: https://github.com/Skybladev2/DobbleMathModel/blob/master/images/Dobble%20incidence%20matrix.png

Fig. 20. La matrice d'incidence du jeu Dobble.
Quelles sont les deux cartes manquantes dans le jeu?
Au total, le tableau avec la matrice d'incidence du jeu comporte 57 lignes et 55 colonnes. Cela signifie que le jeu pourrait avoir 2 cartes supplémentaires.
Cela signifie que les personnages qui devraient figurer sur ces cartes sont moins courants dans le jeu que les autres. Le nombre de personnages dans le jeu est indiqué dans la dernière colonne du tableau.
Le nombre de caractères des cartes manquantes est le suivant:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  et
et 
(14 caractères au total) se produisent 7 fois. se produit 6 fois.
se produit 6 fois.
À quoi ressemblent les cartes manquantes? Pour répondre à cette question, prenez l'un des caractères ci-dessus dans la matrice d'incidence (sauf le bonhomme de neige) et placez-le sur la carte manquante (par exemple, l'avant-dernière colonne).
Ensuite, nous trouvons toutes les cartes (colonnes) sur lesquelles ce symbole est représenté. Cela signifie que sur toutes ces cartes les symboles coïncident, et il ne peut y avoir aucune autre correspondance.
Étant donné que ces cartes ont déjà une correspondance avec le personnage sélectionné, rayez de l'avant-dernière colonne tous les personnages qui apparaissent sur les autres cartes.
Les personnages manquants qui n'ont pas été supprimés et constituent les personnages de l'une des cartes restantes. Puisqu'ils se sont avérés être exactement 8, le type de la deuxième carte manquante est uniquement déterminé.
Voici ces 2 cartes:


Fig. 21. Un type possible de cartes manquantes est le n ° 56 et le n ° 57.
Reste à répondre à la dernière question - l'absence de ces cartes affecte-t-elle la propriété de coïncidence d'un seul symbole entre deux cartes (c'est-à-dire qu'il n'y a soudainement aucune correspondance entre certaines cartes)?
La réponse est évidente, si vous regardez toujours la matrice d'incidence du jeu - non, ce n'est pas le cas. Entre deux cartes (colonnes) est toujours la seule coïncidence.
Pourquoi y a-t-il 2 cartes de moins que le maximum possible dans le jeu?
Initialement, les règles des cinq mini-jeux n'étaient pas dans le livret, mais sur cinq cartes distinctes. En même temps, seulement 60 cartes pouvaient être imprimées. Par conséquent, les auteurs du jeu ont décidé de retirer 2 cartes, de sorte qu'au final, il s'est avéré 55 cartes avec symboles + 5 cartes avec règles. (Remerciements particuliers à Guillaume Gille-Naves pour les éclaircissements.)
Remerciements
J'exprime ma gratitude au réseau de magasins de jeux de société «Igroved» pour leur aide dans la rédaction de l'article.
Merci à Ed Pegg Jr d'avoir fourni l'image de l'avion Fano.
Séparément, je veux mentionner un anonymus et un Maître pour l'aide à la vérification de l'article.
Je remercie le magasin "Table City" pour son aide dans la préparation de la publication de l'article.
Je remercie de tout cœur les auteurs du jeu Igor Polouchine, Denis Blanchot, Guillaume Gille-Naves, ainsi qu'Asmodee pour le droit d'utiliser des images du jeu.