Ternaire équilibré
Je travaille sur un cours de principes d'architecture informatique pour notre université; et en tant que devoir, je voudrais proposer à mes étudiants de construire une machine programmable simple fonctionnant en
ternaire . La raison principale est le plaisir: en tant que conférencier, je dois apporter un peu de divertissement, sinon je ne serai pas écouté. En outre, c'est important pour des raisons historiques. Encore "pourquoi?!" on répondra aux questions "Parce que je peux."
Cette page décrit les bases, elle ne va pas au-delà d'un simple additionneur ternaire (et de son implémentation matérielle). Restez à l'écoute pour en savoir plus.
J'ai choisi le système ternaire équilibré: chaque trit représente l'un des trois états possibles, -1, 0 ou 1. Une description très détaillée de ce système peut être trouvée
ici .

L'élément de base: le multiplexeur ternaire
Abstraction
Le seul bloc qui sera utilisé dans mon ordinateur est le multiplexeur ternaire.
Il peut être vu comme une boîte noire à cinq broches: la broche de sélection reçoit un signal ternaire (-1, 0 ou 1), puis il y a un petit interrupteur à l'intérieur de la boîte qui relie la broche de sortie à l'une des trois broches d'entrée inN, inO ou inP.
Habituellement, il est représenté comme indiqué ici:
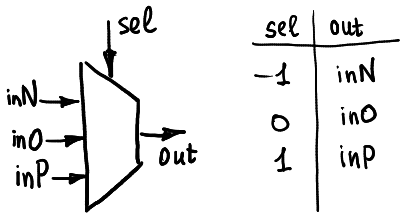
Le démultiplexeur ternaire fonctionne de la même manière: selon la broche de sélection, une entrée est connectée à l'une des trois broches de sortie possibles. Notez que dans mon matériel, j'utilise des commutateurs analogiques CMOS. Ceux-ci sont bidirectionnels, le matériel peut donc être utilisé à la fois comme multiplexeur et démultiplexeur. Mais de toute façon, pour l'instant je n'utilise pas les possibilités de démultiplexage.
Implémentation matérielle
La conception de base a été proposée par
Shaos .
La seule chose que j'ai faite est de créer une version SMD du TRIMUX. Les commutateurs dg403 à montage en surface peuvent être achetés pour 50p par pièce en Chine.
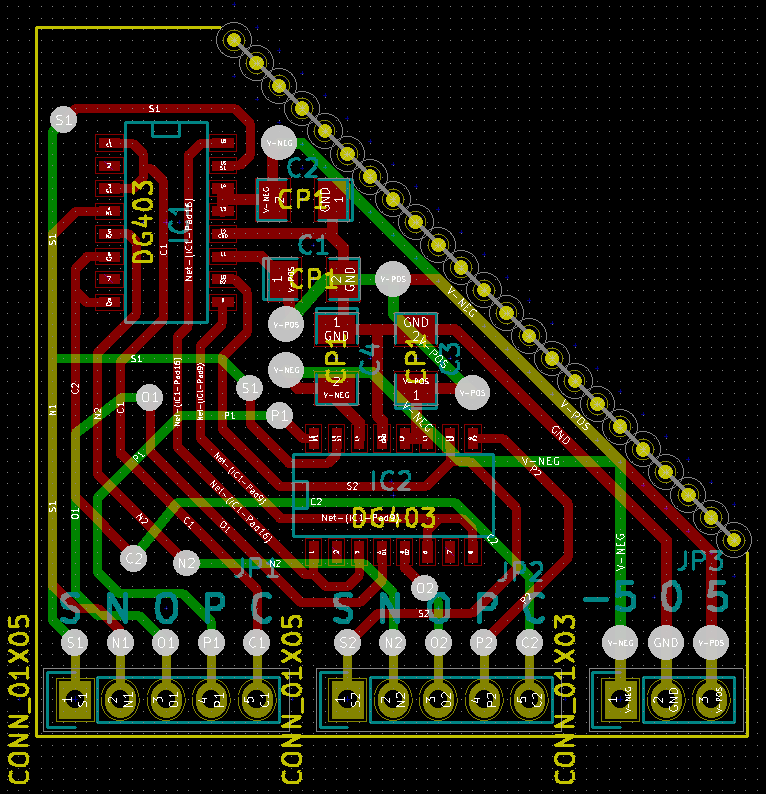
Avant de trouver cette conception, j'ai essayé d'utiliser des combinaisons de cd4007 et cd4016. Cela a fonctionné, mais le matériel est encombrant et laid. Les commutateurs DG403 offrent de véritables possibilités de calcul ternaire sans aucune redondance, comme l'utilisation du binaire deux bits et l'interdiction de l'une des quatre configurations.
Un multiplexeur ternaire peut être créé avec deux DG403: l'un des CI reçoit une alimentation de -5 V à 0 V, tandis que l'autre est alimenté de 0 V à 5 V, et il permet d'utiliser des signaux ternaires représentés par trois tensions -5 V, 0 V et 5 V, respectivement. Cette conception n'utilise que la moitié des broches dg403, il est donc naturel de créer une carte avec deux multiplexeurs.
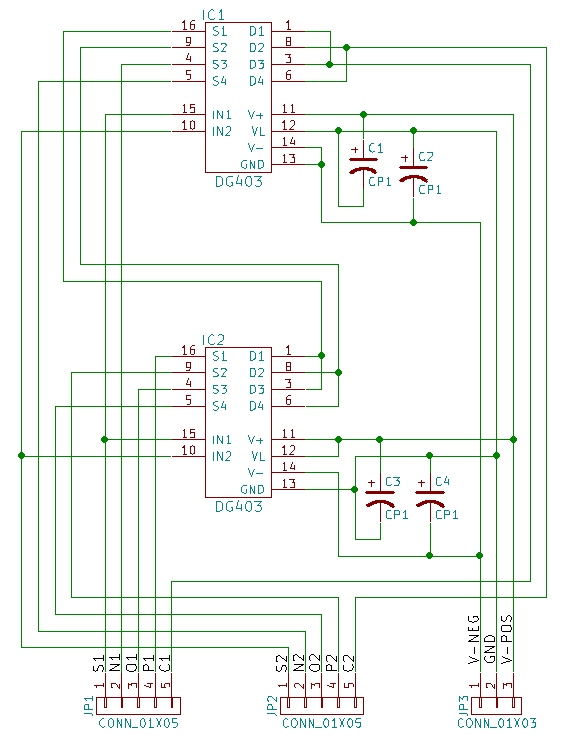
N'hésitez pas à contacter Shaos
ici . Guy incroyable, au lieu de spéculer sur les avantages du ternaire, il a conçu et fabriqué ses propres circuits intégrés ternaires!

Comment l'utiliser? Fonctions unaires
Oublions la fonction d'identité que nous pouvons obtenir en donnant -1.0 et 1 aux broches d'entrée correspondantes du multiplexeur.
Pour commencer, incrémentons le signal d'entrée A en calculant A + 1 (bien sûr, dans l'anneau -1,0,1):
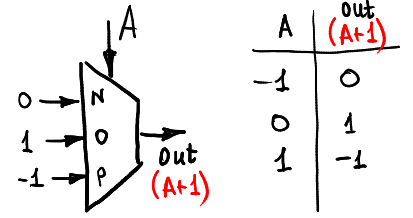
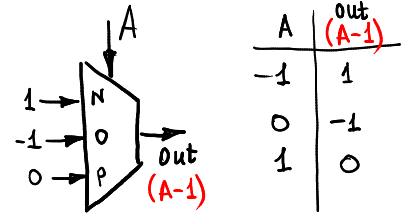
Voici la façon dont nous pouvons décrémenter l'entrée:
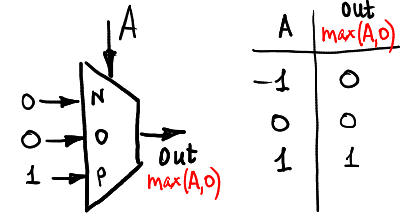
Calculons max (A, 0):
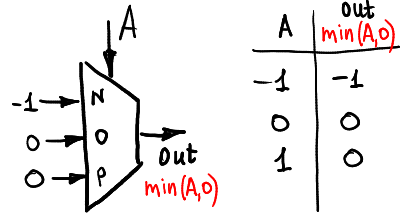
Et le min (A, 0):
Fonctions de deux arguments: demi-additionneur
A + B
Ainsi, un multiplexeur nous permet de calculer n'importe quelle fonction unaire. Pour calculer une fonction de deux arguments, nous devons utiliser trois ou quatre multiplexeurs. Par exemple, si nous voulons calculer une somme de deux signaux A et B (toujours dans l'anneau -1,0,1), alors nous pouvons utiliser ce schéma:
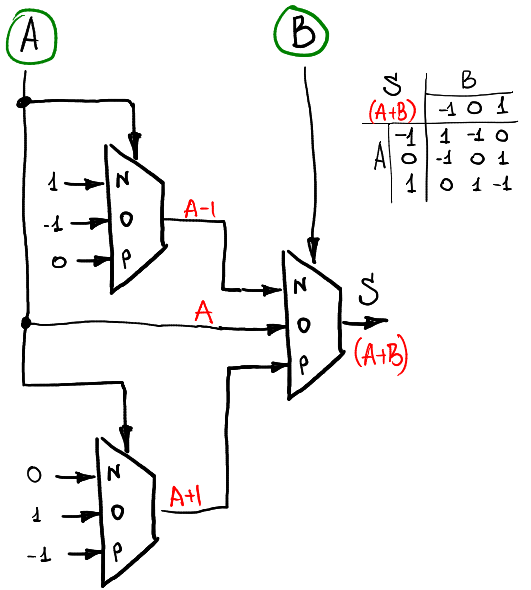
Il existe deux couches de multiplexeurs: la première calcule les fonctions unaires de A et la deuxième couche les combine en fonction de B.
Consensus
Si nous voulons calculer la fonction de consensus de deux signaux ternaires (le consensus est égal à -1 si A = B = -1, est égal à 1 si A = B = 1 et est nul sinon), alors nous pouvons le faire comme ceci:
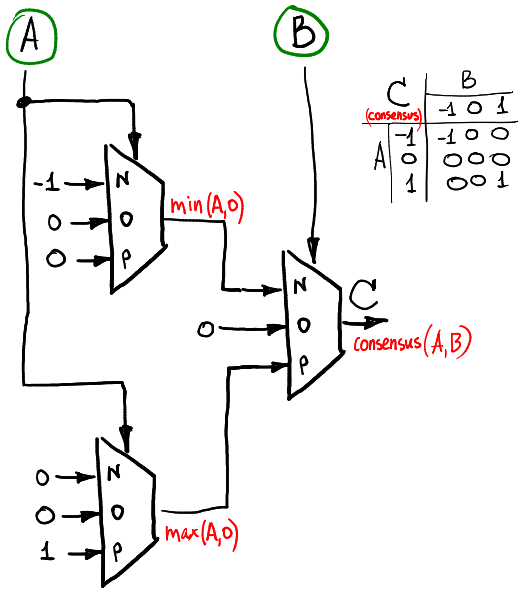
Implémentation matérielle
En fait, nous venons de créer
un demi-additionneur . Pour deux entrées A et B, il calcule deux sorties S et C liées comme A + B = S + 3 * C. S est la somme et C est le drapeau de retenue.
Laissez-nous tester le design! La LED rouge signifie -1, éteinte signifie 0, la LED verte signifie 1. Ainsi, cette photo nous dit que S = -1, C = 1, ou, en d'autres termes, 1 + 1 = -1 + 3 * 1:

Voici le tableau qui répertorie les neuf états possibles de notre demi-additionneur. Chaque cellule donne les valeurs correspondantes pour S et C. Un lien vers une photo est fourni pour chaque cellule.
| S, c | B |
| -1 | 0 | 1 |
| Un | -1 | 1, -1 | -1,0 | 0,0 |
| 0 | -1,0 | 0,0 | 1,0 |
| 1 | 0,0 | 1,0 | -1,1 |
Trois arguments: additionneur complet
Contrairement au demi-additionneur,
un additionneur
complet reçoit trois entrées A, B, Cin et calcule deux sorties S et Cout liées comme A + B + Cin = S + 3 * Cout.
Somme de trois trits
Si nous voulons calculer une somme de A + B + Cin, l'idée est la même que précédemment: nous utilisons une préparation couche par couche des entrées. La première couche reçoit A en entrée, la seconde utilise B et la dernière couche à multiplexeur unique utilise Cin. Voici une façon possible de calculer la sortie S:
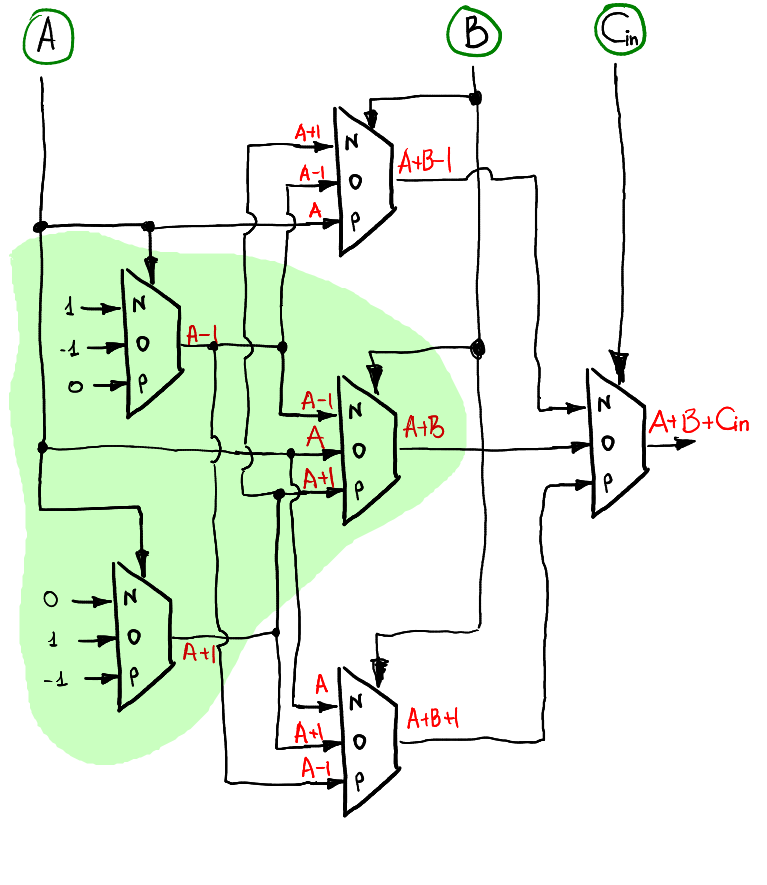
Notez que lorsque Cin = 0, il se comporte exactement de la même manière que le demi-additionneur, il est donc naturel de voir l'inclusion (surlignée en vert) des schémas du demi-additionneur dans l'additionneur complet.
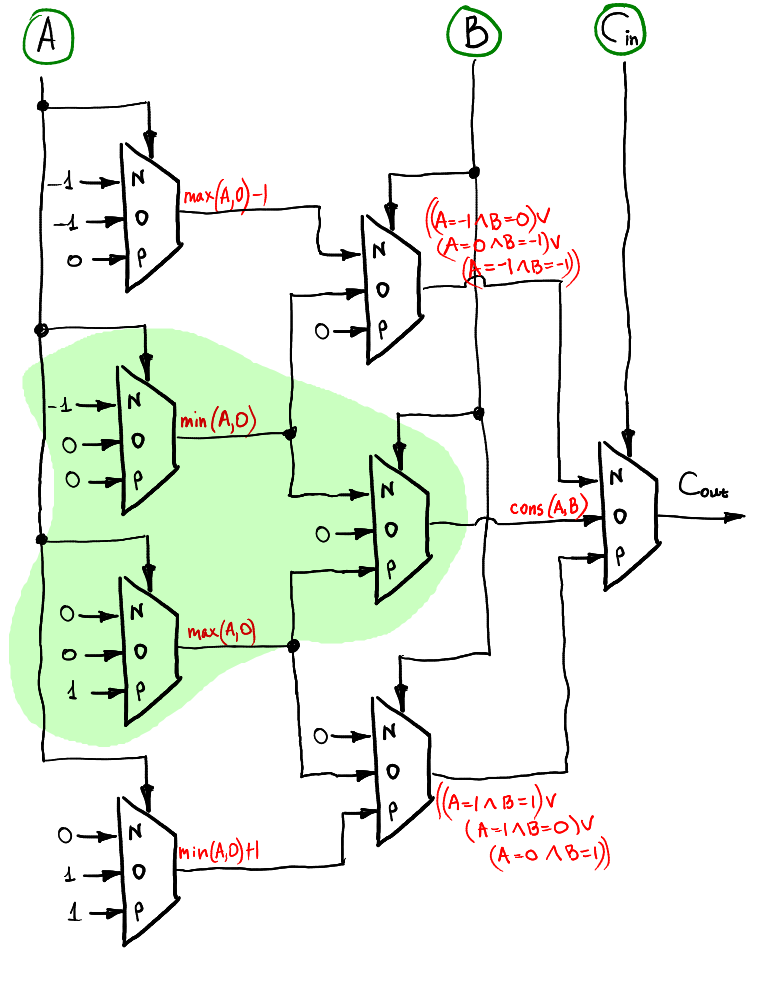
Débordement (drapeau de portage)
Le trit de débordement peut être calculé de la même manière couche par couche. Il comprend également le demi-additionneur!
Validation matérielle
Cette fois, j'étais trop paresseux pour utiliser des cartes d'essai pour tester l'additionneur complet, j'ai donc fait ce PCB à une couche:

Le voici après la gravure du cuivre:

Les trois tableaux suivants répertorient les 27 états possibles de l'additionneur complet. Comme précédemment, les photos sont disponibles pour chaque état. Notez que le tableau du milieu (Cin = 0) est exactement le même que pour le demi-additionneur.
L'avantage de l'additionneur complet par rapport au demi-additionneur est la possibilité d'empiler plusieurs additionneurs jusqu'à ce que nous obtenions suffisamment de trits pour représenter le nombre que nous voulons.
Voici une pile de deux additionneurs:

Et voici comment cela résout -4 + 2 (le trit le moins significatif est à gauche):

Bien sûr, nous n'avons pas besoin d'une carte d'additionneur complète pour le trit le moins significatif (nous n'avons pas d'indicateur de portage pour l'entrée du trit le moins significatif), un demi-additionneur suffirait.
Conclusion
C'est la fin de l'introduction à l'informatique ternaire. Restez à l'écoute pour les horloges, les compteurs, la mémoire et plus encore!