Que nous devrions construire une route. Partie 1

L'itinéraire quotidien de la plupart d'entre nous se limite à voyager de la maison au travail et à l'arrière. Et l'obstacle le plus difficile qui peut ralentir notre mouvement est les embouteillages. Mais dans notre pays, il existe un grand nombre d'endroits où vous ne pouvez monter que sur des véhicules spéciaux.

Un tel transport est bon si vous n'avez pas besoin de transporter de gros volumes de marchandises ou de vous rendre régulièrement dans de telles zones inaccessibles. Ensuite, il faut déjà penser à construire des infrastructures dont la circulation est possible sur les transports civils habituels.

Et c'est bien si toute la complexité de la conception d'un futur itinéraire réside dans la recherche d'une règle et d'un crayon pour tracer une ligne droite sur la carte reliant quelques objets. Mais, hélas, notre réalité est très différente de cela. Et si le terrain qui volait au-dessus ressemblait à un bon morceau de fromage suisse?

Depuis plus d'un an, nous travaillons avec des collègues du laboratoire de recherche Digital Design pour créer un outil permettant de construire différents réseaux de communication en mode automatique. Pour plus de détails, bienvenue au chat.

Comment tout a commencé

En règle générale, les voyages dans ces endroits éloignés sont dus à certains avantages financiers. Et bien que l'on sache souvent à l'avance que le développement de ces domaines apportera de bons profits, pourquoi ne pas économiser de l'argent sur des choses qui peuvent se faire sans difficultés particulières? Et si un tracé plus compétent nous permettait de ne pas construire plusieurs kilomètres supplémentaires de l'autoroute?

Mais seule la disponibilité de routes pour recevoir un profit significatif n'est clairement pas suffisante. Et fondamentalement, il n'est apporté que par des gisements minéraux. Par conséquent, en plus des routes, il est nécessaire de concevoir un réseau de pipelines divers, un réseau de canalisations d'eau, un réseau de lignes électriques avec des sous-stations électriques correctement placées. Toutes ces infrastructures peuvent être désignées comme des objets linéaires.

Et lorsqu'un ingénieur est confronté à la tâche de concevoir un réseau de communication sur le terrain avec des conditions d'ingénierie et géologiques complexes, une tâche analytique incroyablement complexe lui incombe.

Comment ne pas pénétrer dans la zone inondable du fleuve? Comment minimiser le chemin sur les sols de pergélisol? Comment économiser sur la quantité de coussin de sable lors de la pose d'une route à travers un marais? Où trouver du sable pour cet oreiller?

Ce n'est qu'une petite fraction des questions qu'un ingénieur se pose pendant le travail, et pourtant vous devez toujours prendre en compte divers GOST et SNiPs. Et bien, si vous voulez connecter seulement deux objets, et s'il y a quelques dizaines d'objets?

Par conséquent, l'industrie de la conception a un besoin urgent d'un outil capable de calculer à la fois le coût des objets linéaires conçus par un ingénieur et la capacité de les construire en mode automatique.

Les données

La première chose à laquelle nous avons dû faire face lorsque nous avons commencé la tâche était la recherche de données. Quelles données sont nécessaires? Où les obtenir? Et si la deuxième question peut être résolue avec l'aide de l'utilisateur, alors pour comprendre la première question, nous avions besoin d'une analyse sérieuse.

Et les données pour le calcul correct ont vraiment besoin de beaucoup - à partir du marquage le plus banal de la zone sur laquelle les lacs et les rivières sont marqués, divers marécages, ainsi que les zones karstiques, sur lesquelles il est fortement recommandé de ne pas construire en raison de la menace d'effondrement. Par conséquent, en plus des zones visibles depuis le satellite, des données d'études géologiques de la zone sont également nécessaires ici.

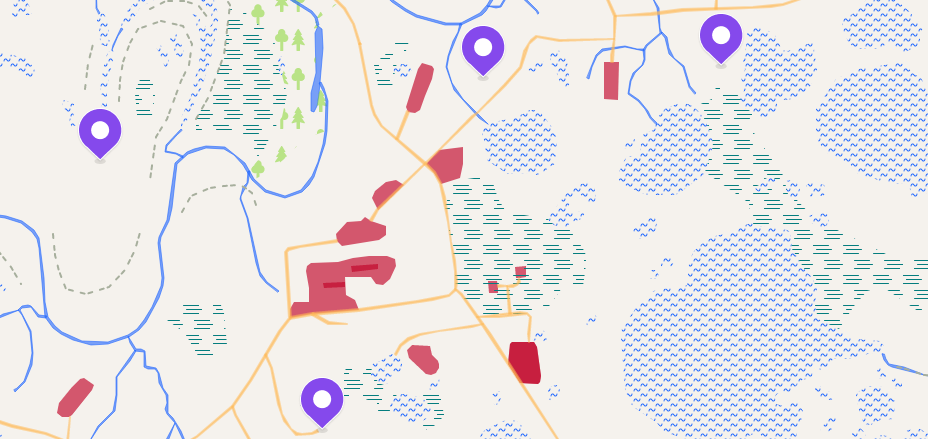
Mais toutes les données ne sont pas limitées aux objets naturels dans notre pays. Il y a aussi un tas de choses qui ont été créées par l'homme. Par exemple, dans le cas de la construction de routes, nous pouvons utiliser les routes construites précédemment. Mais dans la construction de pipelines, l'utilisation des infrastructures existantes est loin d'être toujours possible. Étant donné que la connexion d'un nouveau pipeline à un réseau existant risque de ne pas passer le calcul hydraulique.

En plus de la réutilisation de ce qui a été précédemment créé par l'homme, il faut également prendre en compte diverses restrictions de construction à proximité de tout objet. Par exemple, pour la construction de lignes électriques, vous devez prendre en compte les retraits des lieux d'habitation humains en fonction de la tension sur la ligne électrique elle-même.

Mais il n'est pas tout à fait correct de considérer le calcul du problème uniquement sur un plan, car en plus du terrain plat, il existe des zones avec une grande différence d'altitude, sur lesquelles la construction ne peut pas non plus être effectuée.

L'obtention de données sur le terrain est un processus beaucoup plus simple que les données sur le marquage des zones et les infrastructures existantes. Pour simplifier le développement, nous utilisons des données d'altitude ouvertes SRTM (Shuttle Radar Topography Mission) que tout le monde peut obtenir.

Donc, nous avons les données, nous savons où nous pouvons construire, où nous ne pouvons pas construire, il y a des coûts de construction pour différentes zones du terrain. Nous avons une région, elle a un ensemble d'objets que nous voulons connecter à un seul réseau de communication. En termes mathématiques, cela ressemblera à une recherche d'une solution au problème de Steiner.

Un peu de maths

Il est connu que chaque formule divise par deux le nombre de lecteurs, nous avons donc considérablement réduit cette section ...

Afin d'optimiser le parcours de l'installation linéaire conçue, il est nécessaire de pouvoir calculer son coût de construction. Chaque objet linéaire peut être représenté comme une polyligne $$$L = \ {A_i, B_i \} _ {i = 0} ^ n$ composé de segments $$$AB_ {i}$ .
Le coût de construction de chaque section droite peut être représenté comme une valeur de fonction $$$C_ {AB_ {i}}$ , où chaque segment est spécifié de manière paramétrique:

$$$$ afficher $$ {\ displaystyle AB_i \ colon \ left \ {{\ begin {aligné} & s = s \ left (t \ right) - \ mbox {courbe paramétrée}, \\ & h = h \ left (s (t ) \ droite) - \ mbox {fonction de la hauteur d'élévation}, \\ & c = c \ gauche (s (t) \ droite) - \ mbox {fonction du coût unitaire de construction en un point}, \\ \ end {aligné}} \ droite .} $$ afficher $$

où $$$t \ in \ left [0, 1 \ right]$ - paramétrage des segments.

$$$C_ {AB_i} = \ int \ limits_ {AB_i} c \ left (s (t) \ right) \ sqrt {\ left [g_ {xy} (s (t)) + \ frac {\ partial h} {\ partiel s_x} \ cdot \ frac {\ partiel h} {\ partiel s_y} \ droite] \ dot {s} _ {x} \ dot {s} _ {y}} dt$ où $$$g$ - le tenseur métrique de la surface de la Terre sans tenir compte du relief, c'est-à-dire, en termes simples, la fonction de mesurer la distance à la surface de la Terre.

Étant donné que notre planète a la forme d'un géoïde, il est nécessaire d'utiliser des formules spéciales pour mesurer les distances. Pour cela, nous utilisons la formule Haversinus. Dans celui-ci, la forme de la planète ressemble à une sphère, mais cela suffit pour nos besoins, car l'erreur de mesure est d'environ 0,3% et la vitesse de calcul des distances par cette méthode reste élevée.

Approches pour trouver la meilleure façon

Mais avant de passer à la jonction d'un groupe d'objets, vous devez apprendre à trouver le chemin optimal entre les deux. Deux façons de le faire viennent immédiatement à l’esprit:

1. construire un graphique, puis appliquer les méthodes de recherche de chemin le plus court;
2. utiliser une solution basée sur des méthodes d'optimisation.

Lors de la mise en œuvre de la première méthode, nous avons un problème associé à la méthode de construction d'un graphe pour obtenir la plus grande précision possible de la solution. Il est nécessaire de trouver un équilibre entre le nombre de sommets et d'arêtes dans le graphique, la qualité de la solution et le temps de calcul.

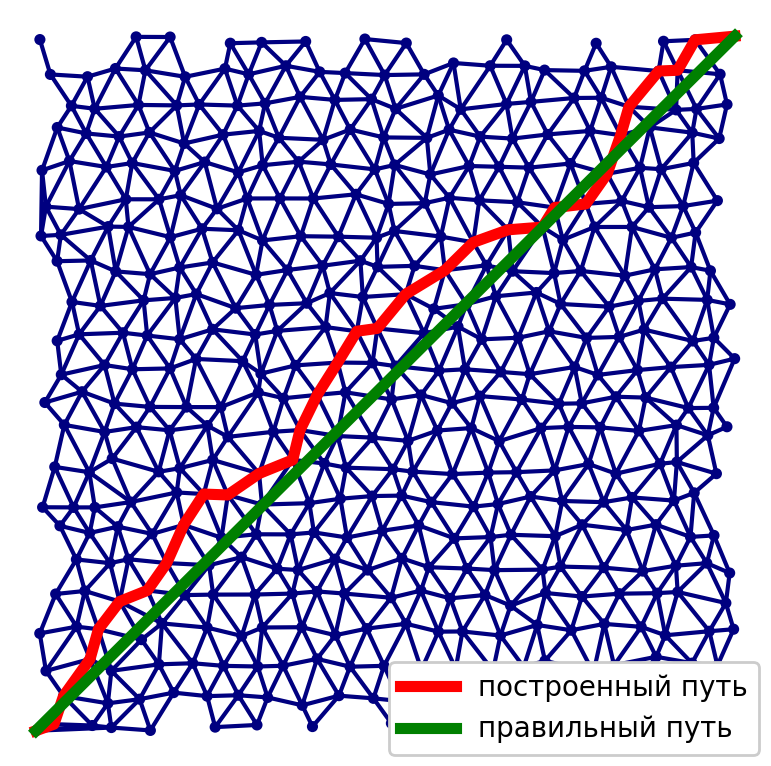
Dans le second cas, le problème principal est les minima locaux. Il est facile de choisir un cas où la solution peut ne pas converger ou être loin d'être optimale. Puisque la solution obtenue par cette méthode dépend incroyablement de l'approximation initiale. Si nous avons une bonne approximation initiale, le résultat sera de haute qualité.

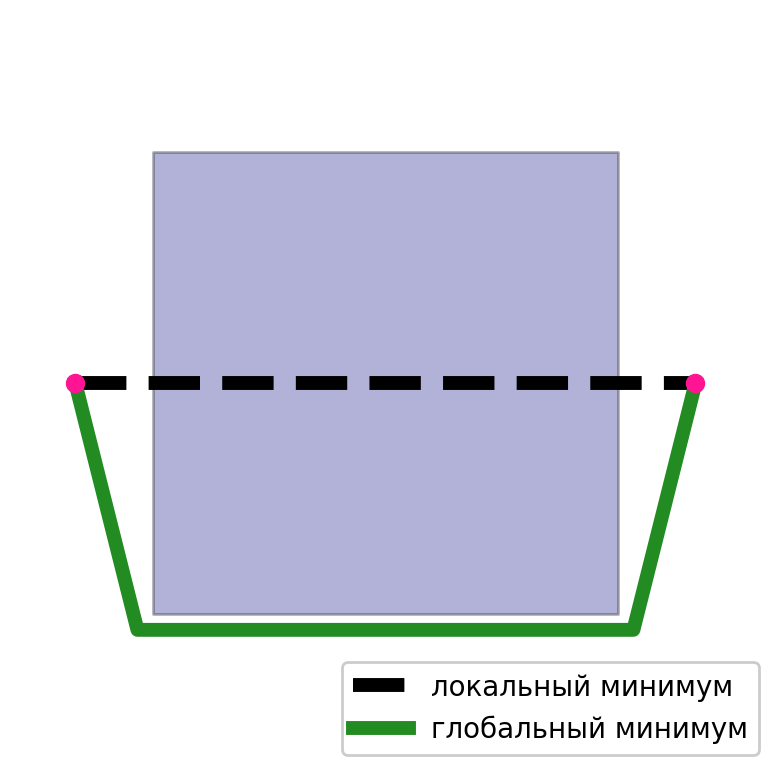
Nous avons donc deux approches pour résoudre ce problème. Le premier a une qualité plutôt faible, mais il n'y a pas de problème de minima locaux. Le second a un problème de minima locaux, mais une solution de haute qualité. Et si vous combinez correctement ces deux approches, les lacunes de chacune disparaîtront. Nous prenons la solution obtenue sur le graphique comme première approximation, puis nous lui appliquons des méthodes d'optimisation.

Dans cette partie de l'article, nous examinerons exactement la solution proposée à ce problème sur le graphique.

Sélection d'outils

Un plan d'action a été esquissé, il ne reste plus qu'à le «coder». Étant donné qu'au stade initial de la rédaction de l'application, nous avions peu de connaissances sur le sujet, nous avions besoin d'un langage flexible, de sorte qu'en cas de mauvais calculs architecturaux, nous réécrivions le code entier pour quelques canettes de bière du soir. Je souhaitais aussi éventuellement des bibliothèques pour toutes les occasions, afin de ne pas recourir à l'invention du vélo. Par conséquent, Python a été choisi comme langage de programmation principal.

Dans l'application, nous avons utilisé une pile technologique impressionnante, qui ne se limite pas aux suivantes:

• bien conçu pour travailler avec des données géométriques telles que des polygones et des polylignes;
• géopandas pour un travail pratique avec bien fait ;
• scipy pour stocker le graphique calculé et trouver le chemin le plus court sur celui-ci, ainsi que pour trouver le minimum d'arbres couvrant;
• PyTorch pour travailler avec la fonction de coût;
• oreiller pour travailler avec des images.

Implémentation

Le module peut être divisé en plusieurs étapes:

• génération de fonctions de coût;
• génération de grille de calcul;
• construire un graphique basé sur une grille;
• pondération graphique;
• calcul des chemins les plus courts sur un graphe.

Étant donné que les bords du graphique sont des segments, nous pouvons pondérer ces bords en calculant la valeur d'une certaine intégrale, qui est présentée ci-dessus. Mais il y a beaucoup d'arêtes dans le graphique et, par conséquent, les valeurs des coûts et des hauteurs devront être obtenues pour un très grand nombre de points, ce qui peut prendre beaucoup de temps.

Initialement, l'idée était de trouver le coût unitaire de construction en déterminant si un point appartient à un polygone. Mais cette idée a été notée en raison de la grande complexité algorithmique de cette approche, car il peut y avoir de nombreux polygones, et chacun d'eux a un grand nombre de sommets.

Par conséquent, pour résoudre ce problème, nous pouvons représenter tous les polygones que nous avons sous la forme d'une image, qui sous forme mathématique est une matrice. Ainsi, nous pouvons obtenir le coût unitaire de construction à un point au-delà de O (1) , et donc nous pouvons obtenir le coût de construction d'une nervure particulière avec une grande précision.

Nous sommes maintenant prêts à construire un graphe, mais il n'y a pas de manière unique et correcte de le construire pour obtenir des solutions de haute précision. Pour construire un graphe, il est nécessaire de générer une grille de calcul, à savoir un ensemble de points dans la région considérée, reliés dans l'ordre correspondant par des segments formant les faces des cellules. Les grilles peuvent être divisées en deux types: uniformes et inégales.

Le modèle de grille uniforme décrit les coordonnées des points individuels, de sorte que la distance entre les nœuds de la grille est la même. Une grille inégale apparaît comme un ensemble aléatoire de points individuels.

L'utilisation d'une grille uniforme ne donnera pas toujours un résultat de haute qualité pour trouver le chemin le plus court, il est donc nécessaire de tester cette approche sur une grille inégale. Le plus polyvalent est le maillage triangulaire.

La grille a été générée en introduisant du bruit avec un certain coefficient dans une grille rectangulaire uniforme, puis en appliquant des points de triangulation Delaunay pour cet ensemble de points.

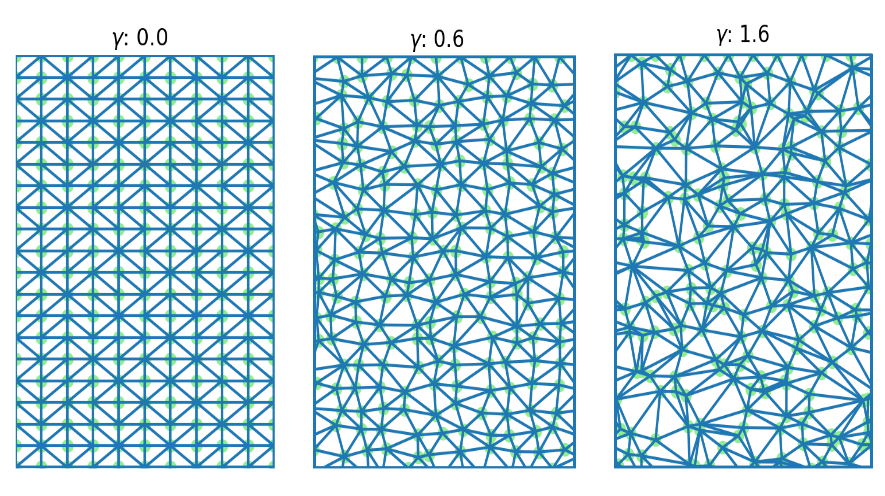
L'efficacité des grilles construites a été testée sur différents modèles de cartes de la zone, qui tenaient compte des différents coûts des régions et du relief, puis une comparaison a été faite avec la solution obtenue analytiquement. En recherchant la longueur du bord du graphique et le coefficient d'introduction de bruit dans la grille uniforme, des paramètres optimaux ont été trouvés pour construire le chemin optimal entre deux points.

Problèmes majeurs

Au début, tout s'est bien passé, l'algorithme a calculé les réseaux optimaux, mais une fois qu'il y a eu un problème avec la qualité du chemin construit. Le cas était assez simple: il fallait connecter deux objets sur une carte assez longue. L'algorithme ne voulait pas construire une route qui était évidemment correcte.

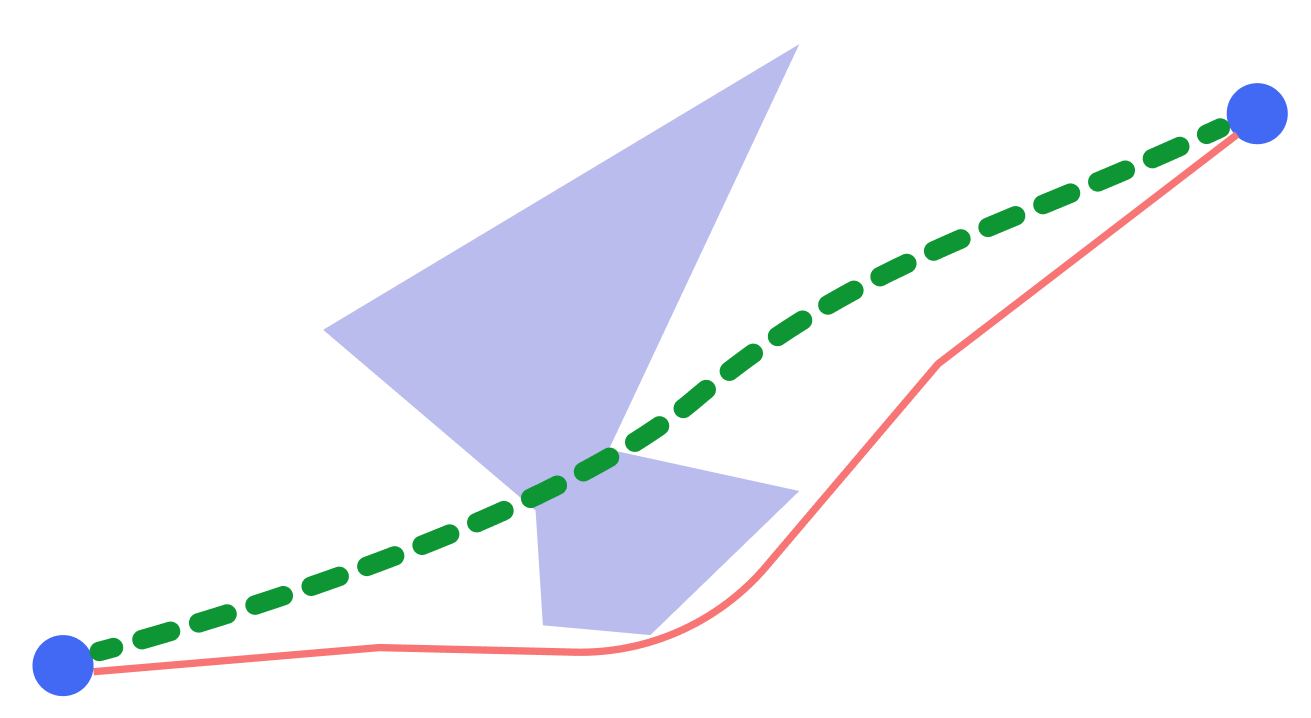
Le problème, comme toujours, était lié à la grille de calcul. Nous avons poursuivi nos expériences avec l'apparition des grilles et sommes arrivés à la conclusion que la connexion des sommets à un graphique, où chaque sommet est connecté aux n voisins les plus proches, est la solution à nos problèmes.

Réseautage

Après avoir appris à trouver des chemins optimaux entre deux points, l'étape suivante a été de résoudre le problème de la construction d'un réseau optimal d'objets linéaires. Les algorithmes rencontrés dans la littérature pour construire des arbres de Steiner sur des graphes sont orientés vers des problèmes plus généraux, et seront donc inefficaces dans notre cas. Notre graphique est très clairsemé, avec un petit nombre de sommets terminaux, par rapport au nombre total de sommets dans le graphique, et notre tâche est également appliquée. Par conséquent, pour un certain nombre d'autres raisons, il a été décidé de développer notre propre algorithme qui utilise une certaine heuristique pour construire efficacement un réseau optimal.

La description de l'algorithme de construction du réseau optimal sur le graphique pour notre cas est un sujet pour une publication séparée, nous ne l'examinerons pas ici. Étant donné que lors du calcul d'une tâche réelle, il est nécessaire de prendre en compte de nombreuses conditions supplémentaires de l'industrie de la construction pertinentes pour l'utilisateur final, qui imposent certaines restrictions à l'algorithme utilisé.

Cas réel

Nous passons maintenant aux résultats de l'algorithme. Notre tâche consiste à connecter un ensemble d'objets donné à un réseau de communication. La comparaison des résultats de l'algorithme s'est produite avec un réseau routier précédemment construit. La longueur totale du réseau existant est de 153,5 km contre 122,6 km pour le réseau calculé. Cela permet une réduction d'environ 25% de la longueur du réseau routier, ce qui permettra à terme d'économiser environ 5 à 15% sur les coûts de construction du capital.

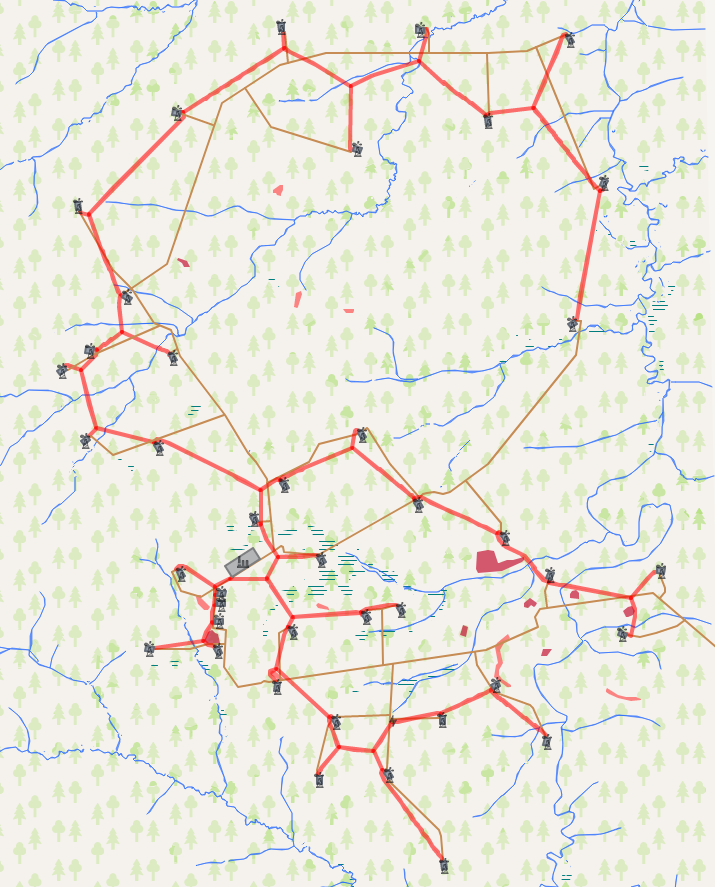
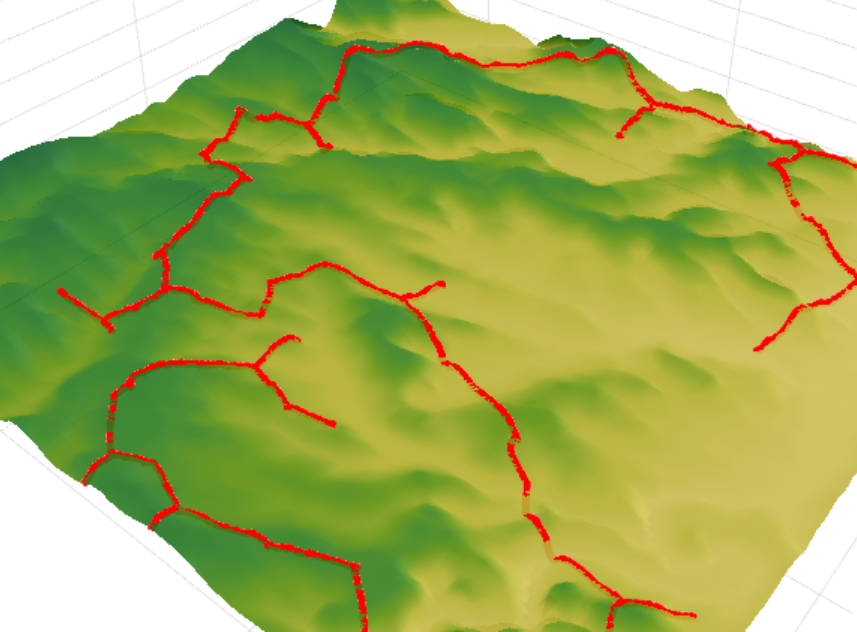
Vous pouvez regarder de plus près les résultats du calcul ici .

Une description des méthodes d'optimisation utilisées sera dans la prochaine partie de l'article.