
Nous avons traduit pour vous un article de Lauri Hartikka sur la création de l'IA la plus simple pour les échecs. Il a été rédigé en 2017, mais les principes de base sont restés les mêmes. Tous les fichiers utilisés par Lori sont également disponibles.
Une intelligence artificielle simple qui peut jouer aux échecs peut être créée sur la base de quatre concepts:
- 1. Déménagement;
- 2. Évaluation du conseil d'administration;
- 3. Minimax ;
- 4. Détourage alpha bêta . À chaque étape de l'utilisation de l'algorithme, l'un d'eux sera utilisé, ce qui améliorera progressivement les capacités de jeu de l'IA.
Skillbox recommande: Le cours en ligne appliqué Python Data Analyst .
Nous vous rappelons: pour tous les lecteurs de «Habr» - une remise de 10 000 roubles lors de l'inscription à un cours Skillbox en utilisant le code promo «Habr».
Le code source prêt à l'emploi peut être trouvé sur
GitHub .
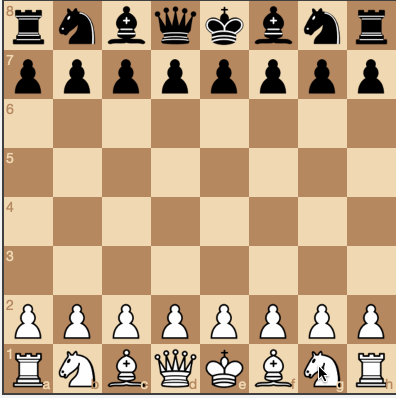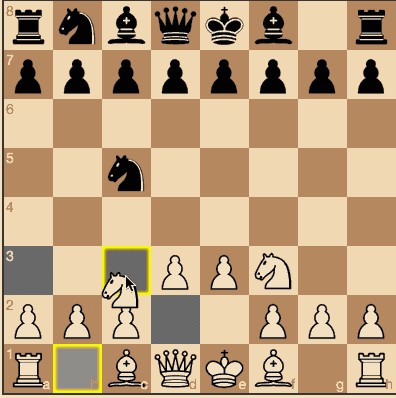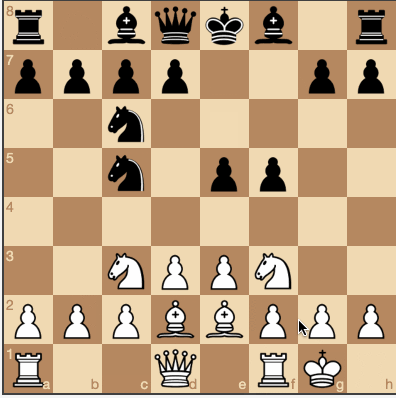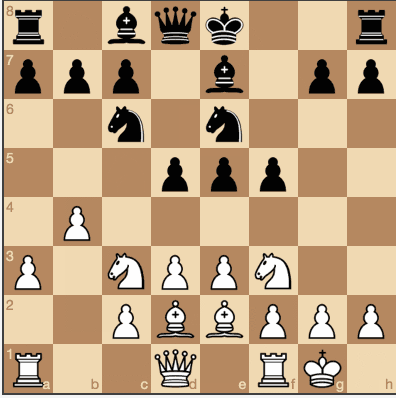
Étape 1. Visualisation d'un échiquier avec génération de mouvements
À ce stade, nous utiliserons les bibliothèques
chess.js pour générer des mouvements et
chessboard.js pour rendre l'échiquier. La bibliothèque, qui est responsable de la génération des mouvements, vous permet d'appliquer toutes les règles d'échecs, afin que nous puissions calculer chaque action pour un arrangement spécifique de pièces.
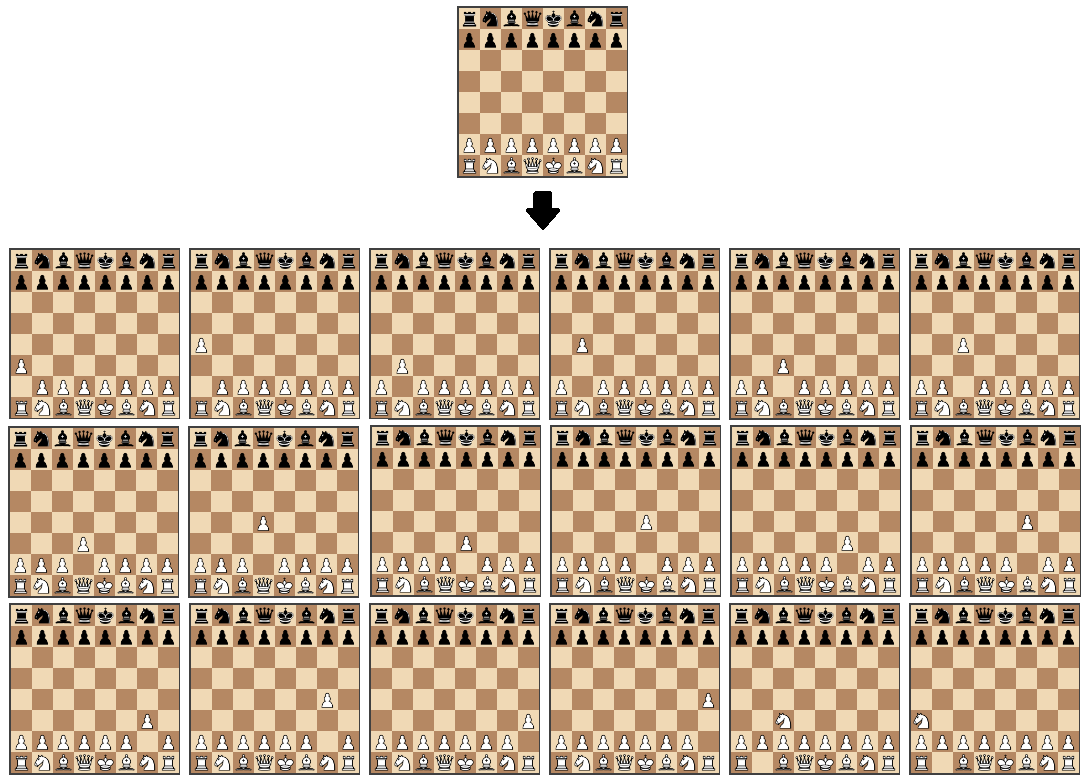
Lorsque vous cliquez sur l'image, elle s'ouvrira en pleine résolution.
Travailler avec ces bibliothèques vous permet de vous concentrer sur la tâche principale - rechercher et créer un algorithme qui vous permet de trouver le mouvement optimal. Nous commençons le travail en écrivant une fonction qui renvoie un mouvement aléatoire à partir d'une liste de toutes les fonctions possibles.
var calculateBestMove =function(game) {
Malgré le fait que l'algorithme n'est pas un joueur d'échecs idéal, cela suffira largement à la plupart des joueurs de son niveau.
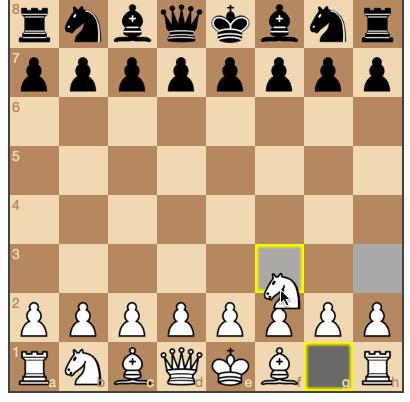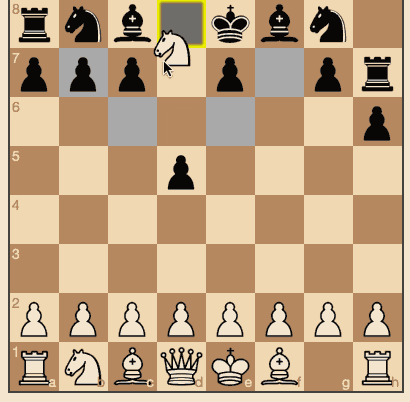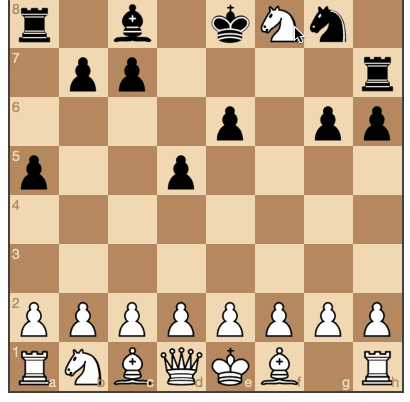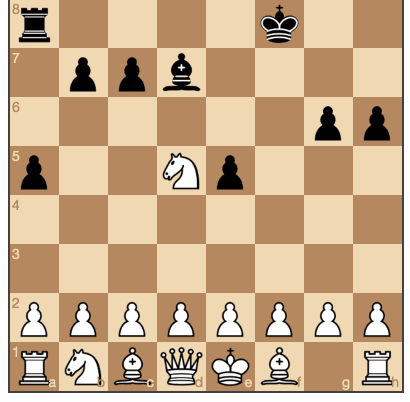
Les noirs se déplacent au hasard. (
source et jeu en ligne )
Étape 2. Évaluation du poste
Voyons maintenant quel côté a l'avantage dans telle ou telle position. Le moyen le plus simple est de calculer la force relative des pièces sur la planche, cela peut être fait en utilisant le tableau.

En utilisant la fonction d'évaluation, nous avons la possibilité de créer un algorithme qui sélectionne le mouvement avec la note maximale.
var calculateBestMove = function (game) { var newGameMoves = game.ugly_moves(); var bestMove = null;
En principe, le niveau est le même, mais l'algorithme peut déjà prendre la figure de quelqu'un d'autre quand une telle opportunité existe.
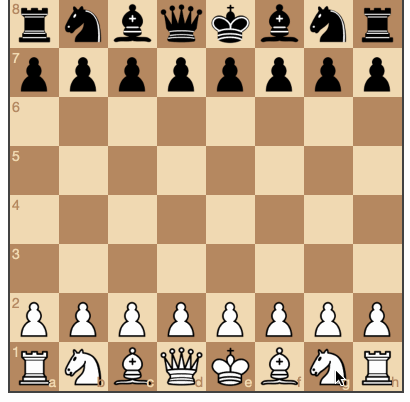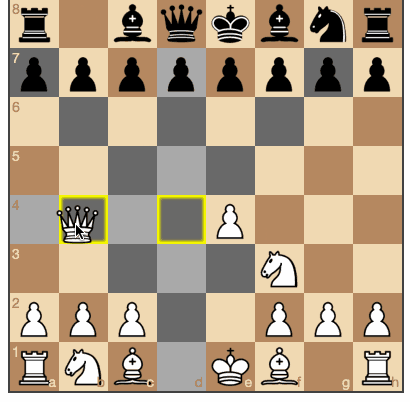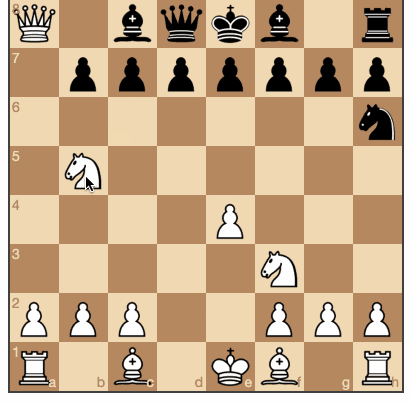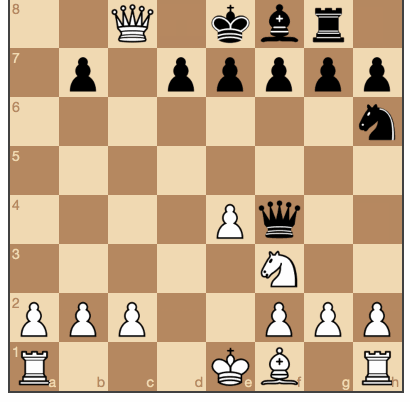
Les noirs ont eu l'occasion de prendre des pièces blanches. (Les sources et le jeu sont
ici ).
Étape 3. Arbre de recherche avec minimax
Après cela, nous créons un arbre de recherche. Maintenant, le programme peut choisir le meilleur mouvement. Cela se fait en utilisant l'algorithme minimax.
Ici, un arbre récursif avec l'affichage de tous les mouvements possibles est analysé à une profondeur donnée. La position est estimée par les feuilles de notre arbre.
Ensuite, nous renvoyons la valeur minimale ou maximale de l'enfant au nœud parent. Tout dépend de quel côté est actuellement mal calculé. En d'autres termes, le résultat est maximisé ou minimisé à chaque niveau.
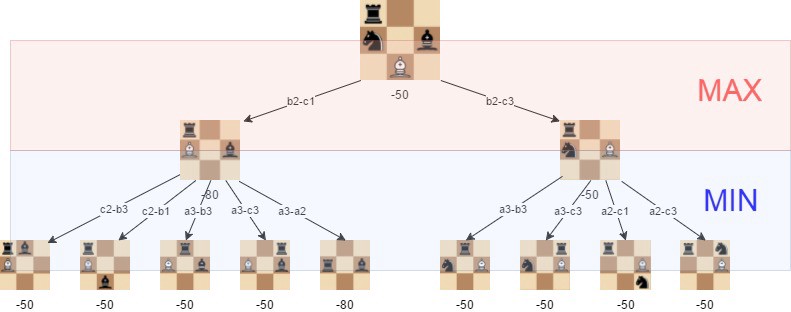
Ici, b2-c3 est le meilleur coup pour les blancs, car il s'assure que le joueur arrive à la position avec un score de -50.
var minimax = function (depth, game, isMaximisingPlayer) { if (depth === 0) { return -evaluateBoard(game.board()); } var newGameMoves = game.ugly_moves(); if (isMaximisingPlayer) { var bestMove = -9999; for (var i = 0; i < newGameMoves.length; i++) { game.ugly_move(newGameMoves[i]); bestMove = Math.max(bestMove, minimax(depth - 1, game, !isMaximisingPlayer)); game.undo(); } return bestMove; } else { var bestMove = 9999; for (var i = 0; i < newGameMoves.length; i++) { game.ugly_move(newGameMoves[i]); bestMove = Math.min(bestMove, minimax(depth - 1, game, !isMaximisingPlayer)); game.undo(); } return bestMove; } };
Avec l'algorithme minimax, notre IA a déjà commencé à comprendre les tactiques de base des échecs.
Minimax avec une profondeur de 2 (Sources et jeu
ici )
Il convient de noter que l'efficacité de l'algorithme minimax augmente avec la profondeur de la recherche. La prochaine étape en est responsable.
Étape 4. Alpha Beta Clipping
Il s'agit d'une méthode d'optimisation de l'algorithme minimax qui permet d'ignorer certaines branches de l'arbre de recherche. Et cela vous permet d'augmenter la profondeur de recherche, en dépensant la même quantité de ressources.
L'écrêtage alpha bêta est basé sur une situation où nous pouvons arrêter d'évaluer une certaine branche s'il s'avère qu'un nouveau mouvement conduira à une situation pire que celle que nous avons vue lors de l'évaluation de la précédente.
L'optimisation n'affecte pas le résultat de minimax, mais tout commence à fonctionner plus rapidement.
Cet algorithme est beaucoup plus efficace si vous vérifiez d'abord les chemins menant à de bons mouvements.
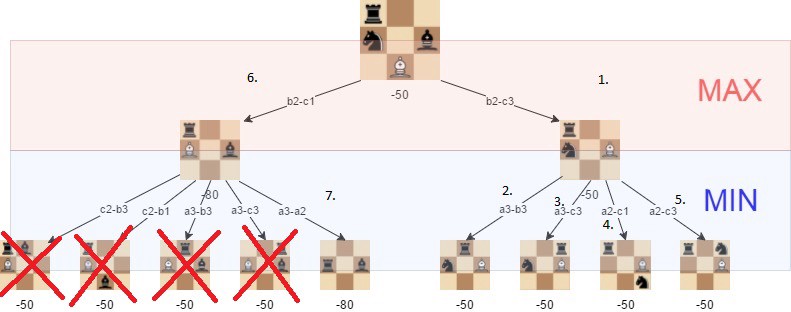
L'image montre des mouvements qui deviennent inutiles lors de l'utilisation de l'écrêtage alpha bêta.
Comme vous pouvez le voir, avec l'écrêtage alpha-bêta, minimax est optimisé, et de manière très significative.

Le nombre de positions que vous souhaitez évaluer dans le cas d'une recherche avec une profondeur de 4 et la position de départ, indiquée ci-dessus. (la source et le jeu sont disponibles
ici )
Étape 5. Fonction d'évaluation améliorée
La fonction d'évaluation initiale est assez simple, car elle compte simplement les points des pièces sur le plateau. Pour l'optimiser, vous pouvez prendre en compte la position des figures. Par exemple, si vous placez le cheval au centre de la planche, cela devient plus cher - la gamme de mouvements disponibles pour cette pièce s'élargira.
À ce stade, nous travaillerons avec une version légèrement modifiée des tables carrées décrites à l'origine dans le
wiki Chess Programming .
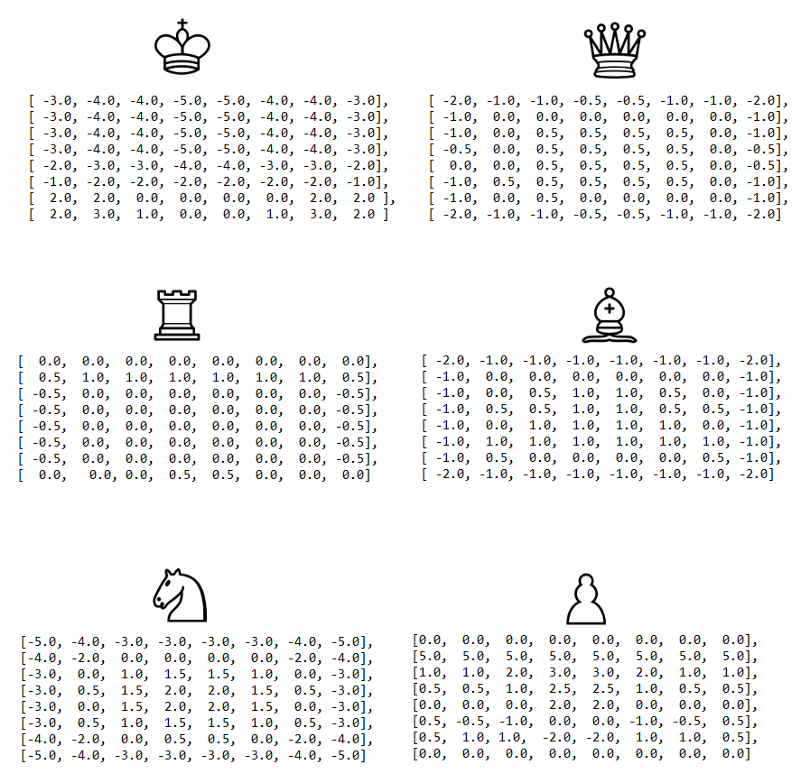
Et maintenant, notre algorithme fonctionne déjà assez bien, bien sûr, par rapport au joueur moyen.
Les sources et le jeu sont disponibles
ici.Conclusion
L'avantage de l'algorithme proposé est qu'il ne fait pas d'erreurs très stupides. Bien sûr, la stratégie ici ne peut guère être qualifiée de parfaite, mais néanmoins.
L'implémentation de notre algorithme ne comprend que 200 lignes de code, donc les principes de base sont assez simples. La version finale du programme peut être <a href= target
github.com/lhartikk/simple-chess-ai'> vue sur GitHub.
D'autres modules peuvent être ajoutés à l'algorithme, notamment:
Plus d'informations sur les algorithmes d'échecs peuvent être trouvées sur le
wiki de programmation d'échecs .
Skillbox recommande: