De nombreux développeurs pensent que la disposition automatique est un frein et un problème, et il est extrêmement difficile de la déboguer. Et c'est bien si cette conclusion est faite sur la base de ma propre expérience, et parfois c'est juste "J'ai entendu, je n'essaierai même pas de me faire des amis".
Mais peut-être que la raison n'est pas à l'extérieur, mais à l'intérieur. Par exemple, les oiseaux les plus dangereux du monde du casoar n'attaqueront pas les gens sans raison, uniquement pour se défendre. Par conséquent, essayez de supposer une seconde que ce n'est pas une mauvaise disposition automatique, que vous ne la comprenez pas assez bien et ne savez pas comment cuisiner. C'est ce qu'Anton Sergeyev a fait et s'est plongé dans la théorie afin de tout comprendre exactement. On nous offre une compression prête à l'emploi sur les fondements mathématiques de la mise en page automatique.
La mise en page automatique est un
système de mise en page . Avant de nous y plonger, parlons de la composition moderne en général. Ensuite, traitons de la
disposition automatique - nous déterminerons
quelle tâche elle résout et comment elle le fait. Examinons les
fonctionnalités de l'implémentation de la mise en page automatique dans iOS et essayons de développer
des conseils pratiques qui peuvent vous aider à travailler avec.
Cette histoire sera très proche d'un article mathématique, donc on s'entend d'abord sur la notation pour parler le même langage.
À propos du conférencier: Anton Sergeev (
antonsergeev88 ) travaille dans l'équipe Yandex.Mart, s'occupe du client mobile pour Maps sur iOS. Avant le développement mobile, il a traité des systèmes de contrôle des centrales électriques, où le coût des erreurs dans le code est trop élevé pour être toléré.
Désignations
Les systèmes d'équations linéaires nous sont familiers depuis l'école - ils sont indiqués par un crochet et leur solution est déjà sans. De plus, les systèmes d'équations linéaires ont des entités qui fonctionnent avec des restrictions de disposition automatique. Ils sont indiqués par une ligne droite.
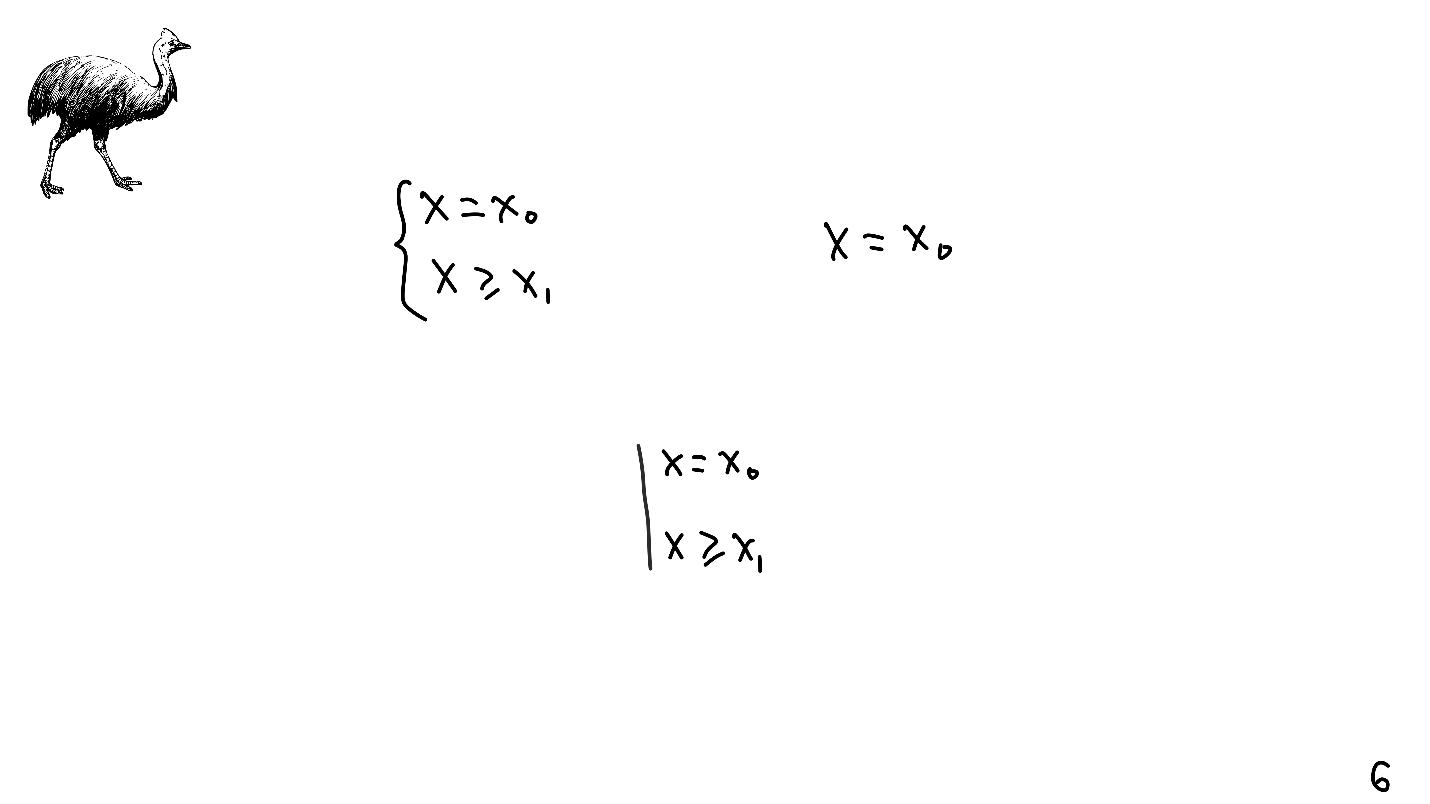
L'oiseau étrange et, comme nous le savons déjà, dangereux n'est pas accidentellement peint dans le coin supérieur du toboggan. En l'honneur du casoar (casoar lat.), Qui, bien sûr, vit en Australie, un algorithme est nommé dans tous nos iPhones.
La disposition automatique a ses propres limites, nous les désignerons par des couleurs par ordre de priorité: rouge - obligatoire; jaune - haut; bleu - bas.
Disposition
Lors de la rédaction de la présentation, j'ai placé divers éléments à l'écran, par exemple un casoar. Pour ce faire, j'ai déterminé que le casoar était une image rectangulaire. Vous devez l'organiser sur une feuille qui a des axes et son propre système de coordonnées, et pour cela j'ai déterminé les coordonnées du coin supérieur gauche, la largeur et la hauteur.
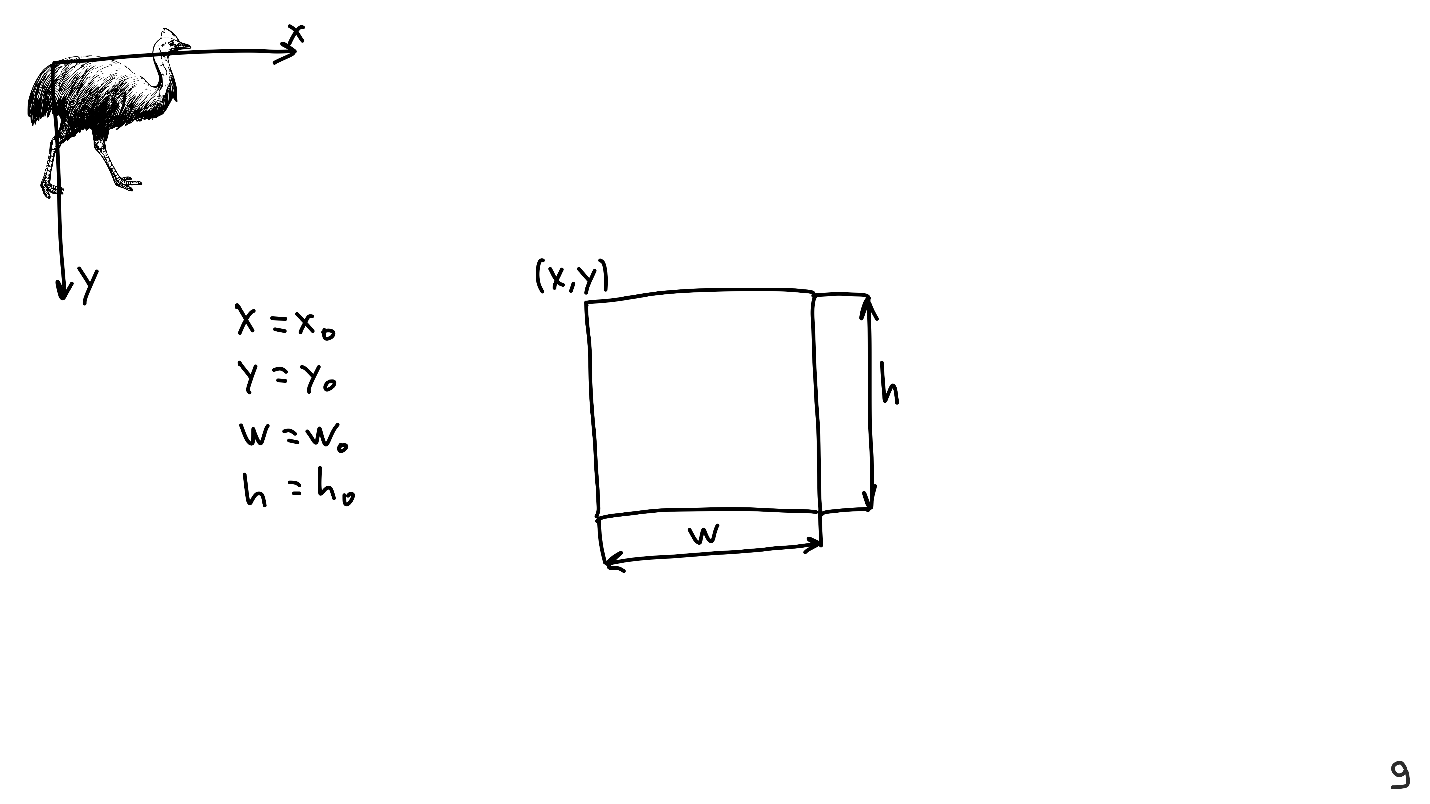
Connaître ces quatre valeurs suffit pour représenter n'importe quelle vue.
Algorithme n ° 1
En plaçant le casoar sur la feuille, nous avons discrètement décrit le premier algorithme de mise en page:
- déterminer les coordonnées et les tailles;
- appliquez-les à UIView.
L'algorithme fonctionne, mais est assez difficile à utiliser, nous allons donc le simplifier davantage.
Supposons que ci-dessous soit une solution à un système d'équations linéaires.
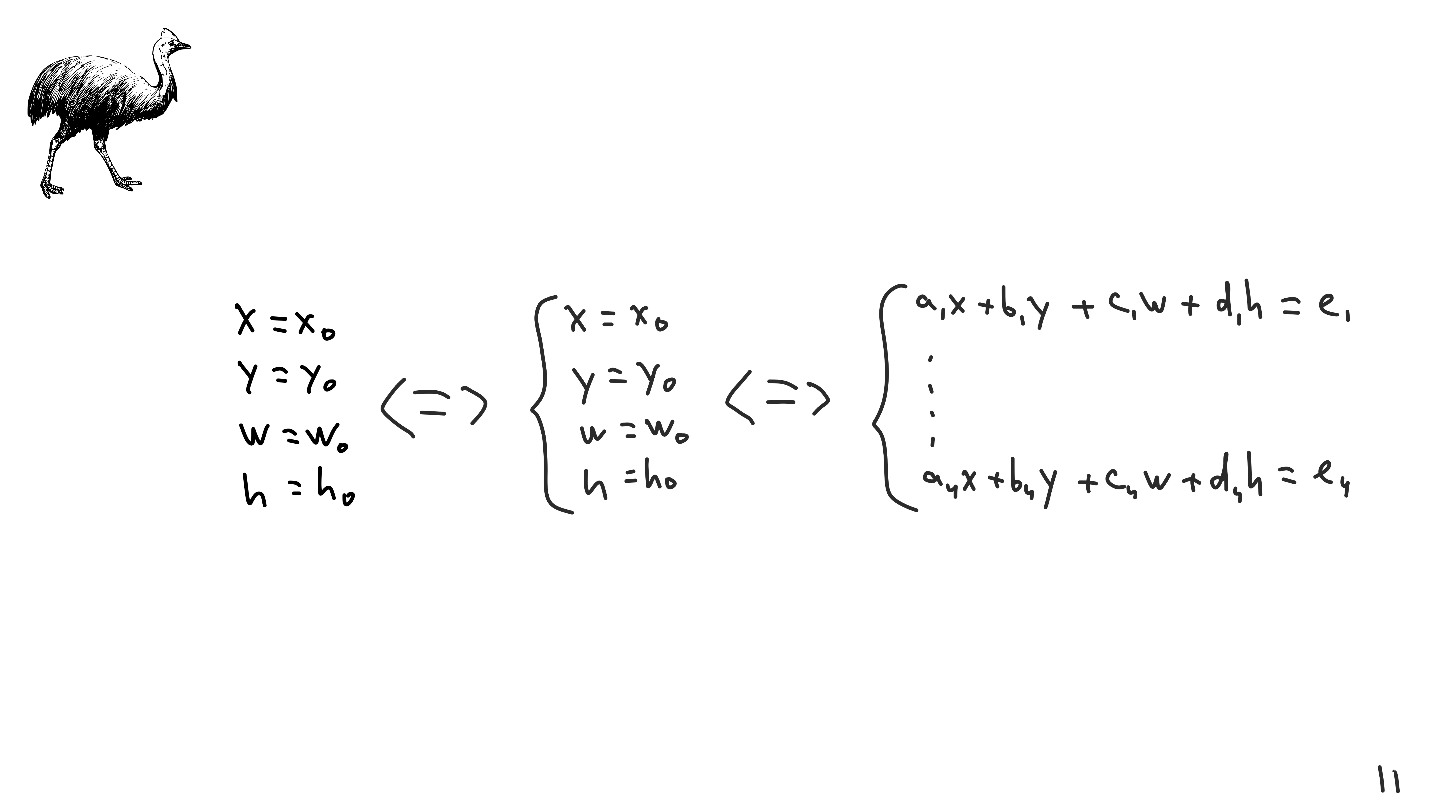
Le système d'équations linéaires est particulier en ce que de nombreuses opérations y sont définies: pliage de lignes, multiplication par constantes, etc. Ces opérations sont appelées transformations linéaires et, avec leur aide, le système est réduit à une forme arbitraire.
La beauté des transformations linéaires est qu'elles sont réversibles. Cela nous amène à une idée intéressante et plutôt subtile avec laquelle commence toute la mise en page moderne.
Soit une vue - un rectangle avec ses coordonnées et sa taille. Nous voulons l'arranger pour que le centre coïncide avec le point donné. Nous modélisons le centre à l'aide de transformations linéaires - les
coordonnées du coin supérieur gauche + la moitié de la largeur .
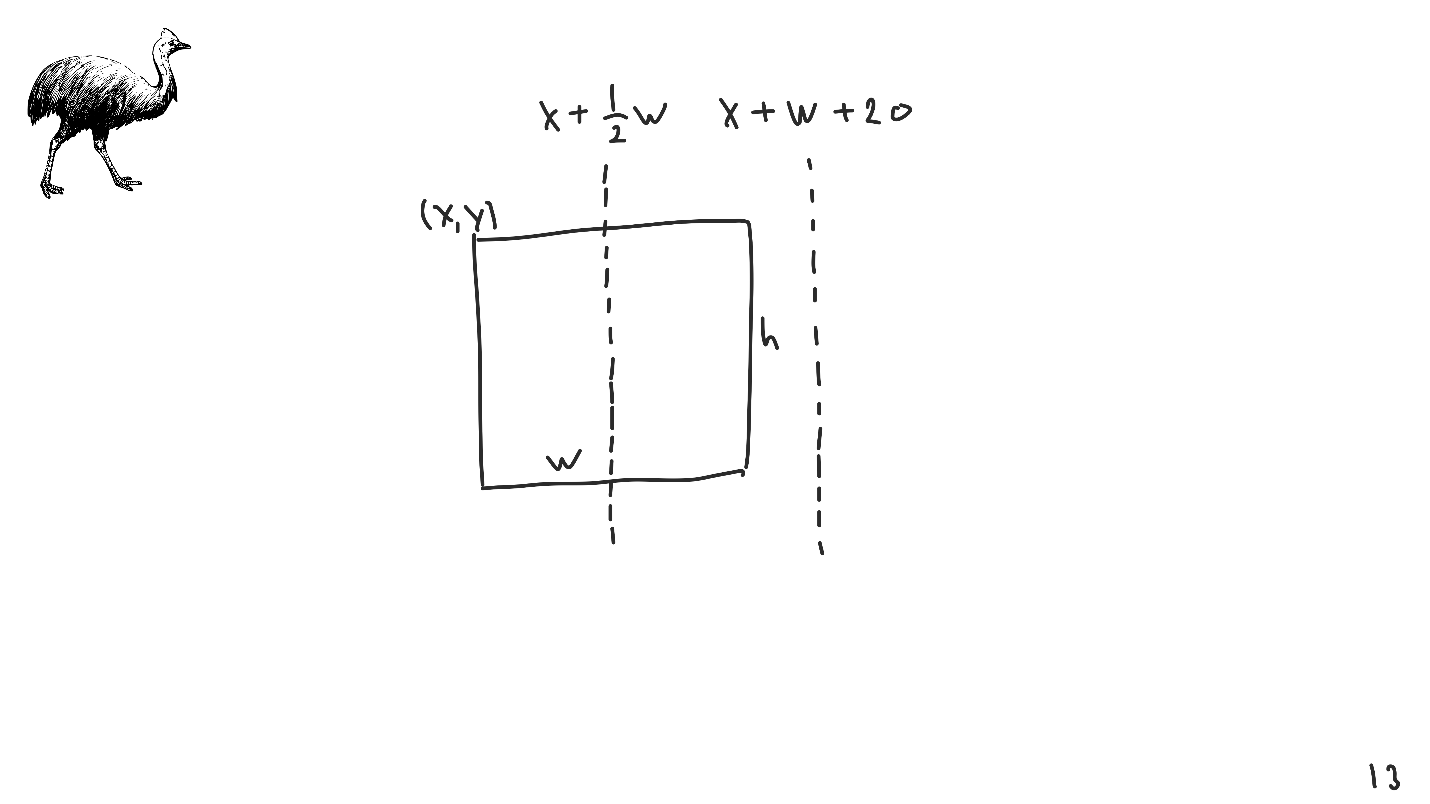
Nous avons modélisé le centre par transformation linéaire, ce n'était pas le cas: il n'y avait que les coordonnées du point supérieur gauche, la largeur et la hauteur.
De même, vous pouvez simuler toute autre indentation, par exemple, à 20 points du coin droit.
C'est l'idée de transformations linéaires qui nous permet de créer différents systèmes de composition.
Prenons un exemple élémentaire. Nous écrivons un système avec lequel nous établissons les coordonnées du milieu et du côté droit, la largeur et la relation entre la largeur et la hauteur. Nous résolvons le système et obtenons la réponse.
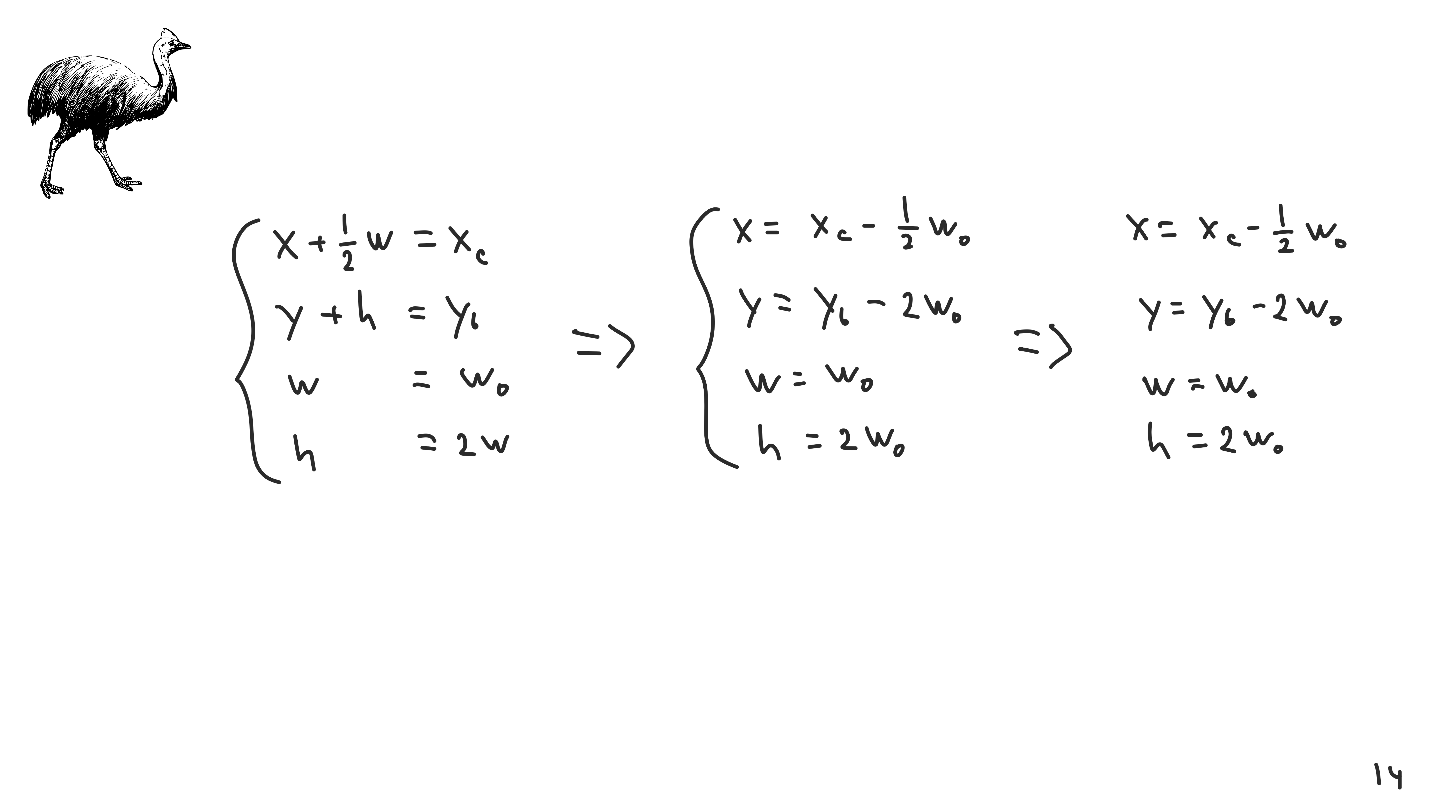
Nous arrivons donc au deuxième algorithme.
Algorithme n ° 2
La deuxième itération de l'algorithme se compose des éléments suivants:
- constituer un système d'équations linéaires;
- nous le résolvons;
- appliquer la solution à UIView.
Imaginez que nous étions au XXe siècle, à une époque où l'équipement informatique n'en était qu'à ses balbutiements, et que nous avons été les premiers à créer notre propre système de mise en page. Inventé, emballé, donné à l'utilisateur, et il commence à l'utiliser - remplit les paramètres initiaux et le transfère à notre système.
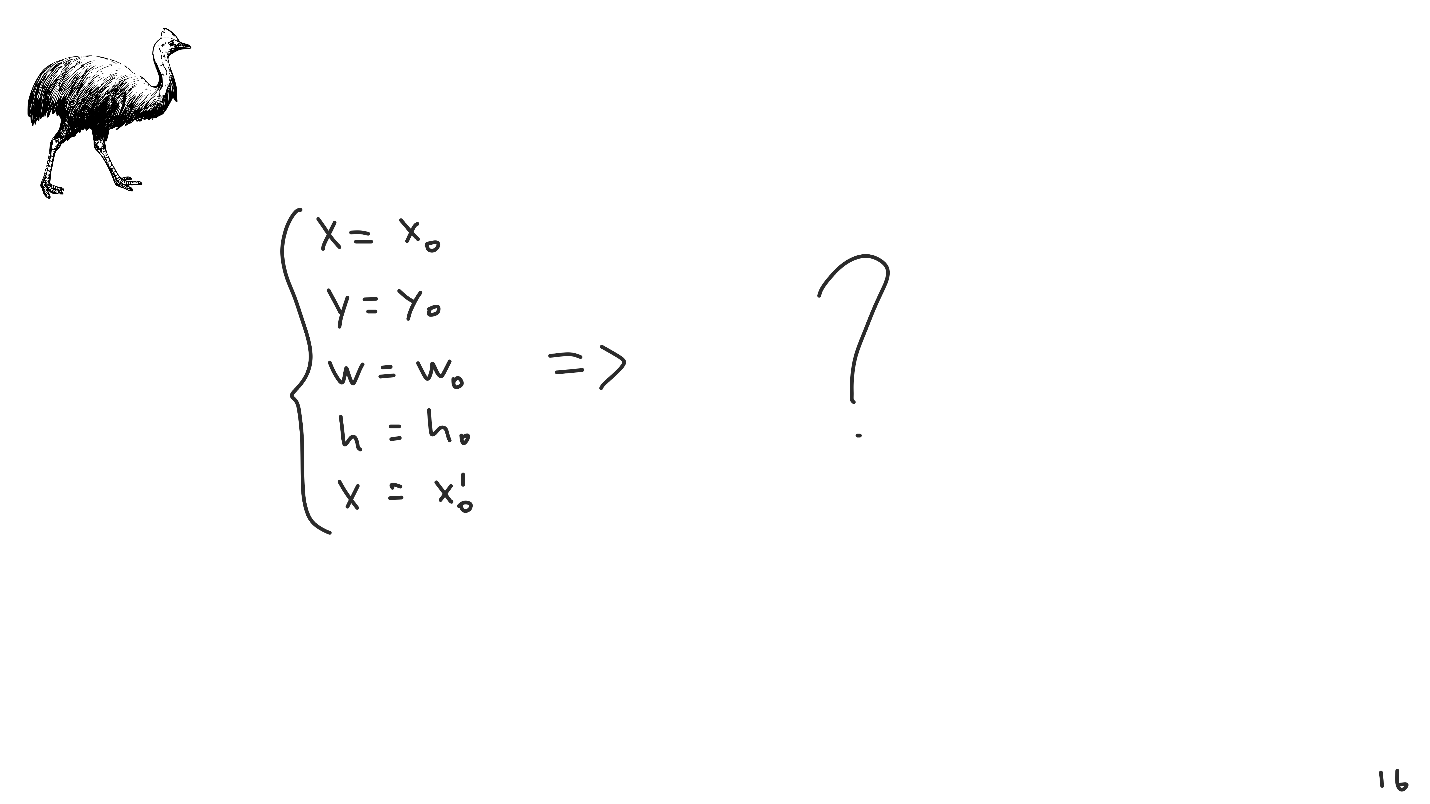
Il y a un problème - ce système n'a pas de solution unique. Le problème n'est pas exceptionnel, absolument tous les systèmes de mise en page s'y heurtent, et est appelé le
manque de solution .
Il n'y a pas tant de façons de sortir de cette situation:
- Vous pouvez tomber - c'est une méthode très courante. Ceux qui travaillent avec MacOS savent que NSLayoutConstraintManager fait exactement cela.
- Renvoie la valeur par défaut . Dans le cadre de la mise en page, nous pouvons toujours retourner tous les zéros.
- Une manière plus connue et délicate consiste à empêcher une entrée incorrecte . Cette méthode est utilisée par les systèmes de mise en page populaires, par exemple le Yoga , appelé Flex Layout . Ces systèmes essaient de créer une interface qui ne permettra pas une entrée incorrecte.
- Il y a une autre façon de résoudre absolument tous les problèmes - de tout repenser dès le début et d'abord d'éviter l'apparition de ce problème . La disposition automatique s'est déroulée de cette façon.
Disposition automatique Énoncé et solution du problème
Nous avons une image rectangulaire et pour l'identifier de manière unique, nous avons besoin de 4 paramètres:
- coordonnées du coin supérieur gauche;
- largeur et hauteur.
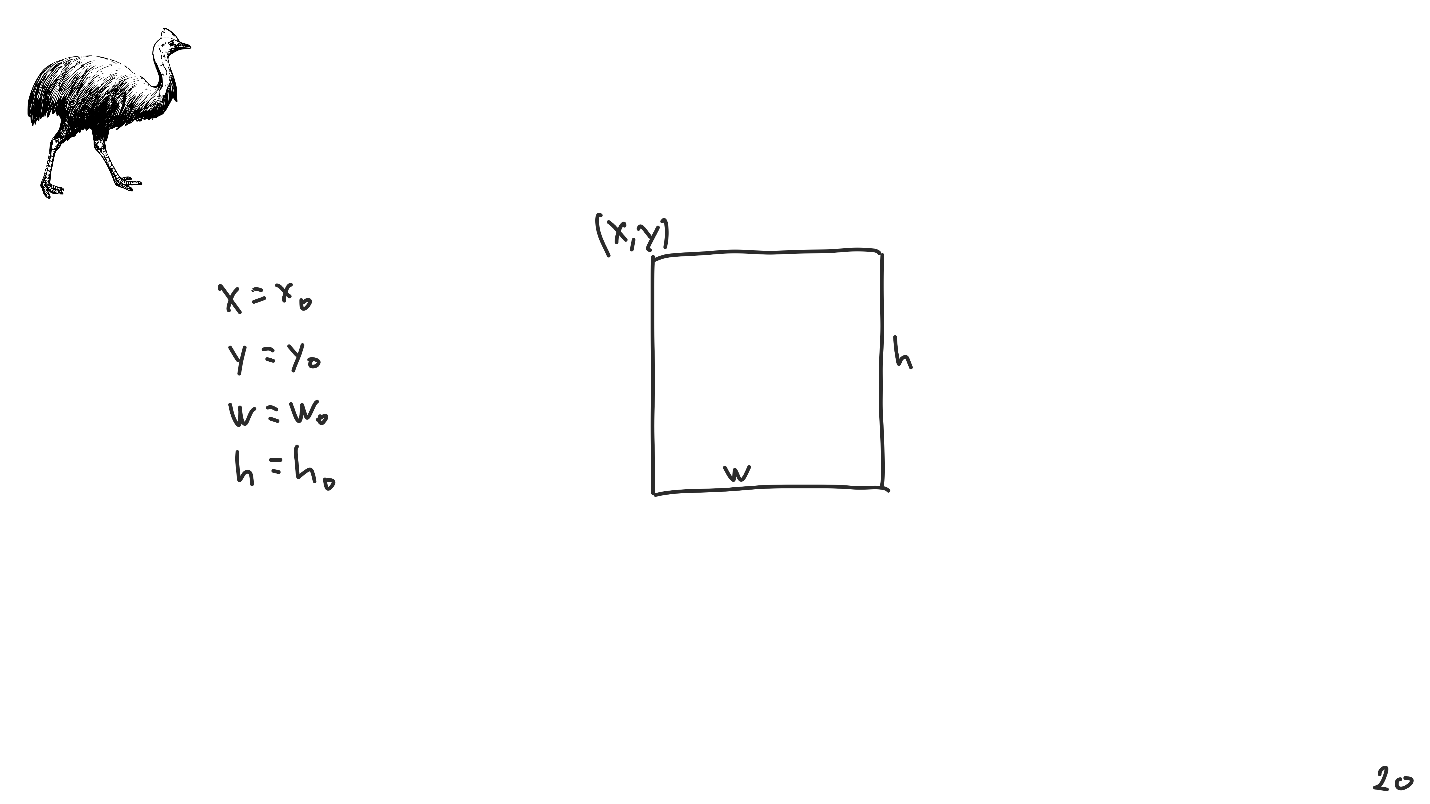
La mise en page automatique est très détaillée. Comparé à un système d'équations linéaires, il est beaucoup plus difficile de tout placer sur l'écran avec lui. Par conséquent, nous considérerons, sans perte de généralité, le cas unidimensionnel.

Tout est très simple: l'espace est une ligne droite, et tous les objets qui peuvent y être placés sont des points sur une ligne droite. Une valeur:
X = X P suffit pour déterminer la position du point.
Considérez l'approche de mise en page automatique. Il existe un espace dans lequel des restrictions sont définies. La solution que nous voulons obtenir est
X = X 0 , et aucune autre.
Il y a un problème - nous n'avons pas défini d'opérations avec des restrictions. Nous ne pouvons pas conclure directement de l'enregistrement que
X = X 0 , nous ne pouvons rien multiplier ou ajouter quoi que ce soit à quoi que ce soit. Pour ce faire, nous devons transformer la contrainte en ce avec quoi nous pouvons travailler - en un système d'équations et d'inégalités.

La disposition automatique transforme un système d'équations et d'inégalités comme suit.
- Introduit d'abord 2 variables supplémentaires qui ne sont pas négatives et dépendent les unes des autres . Au moins l'un d'eux est égal à zéro.
- La contrainte elle-même est convertie en notation X = X 0 + a + - a - .
Point
X 0 - solution du système: si
a + et
a - sont égaux à zéro, alors ce sera vrai. Mais
tout autre point sur cette ligne sera une solution.
Par conséquent, il est nécessaire de trouver le meilleur parmi l'ensemble des solutions. Pour ce faire, nous introduisons une fonction - une fonction ordinaire qui renvoie un nombre, et nous pouvons comparer les nombres. Nous dessinons un graphique et notons que la solution que nous voulions à l'origine est un minimum.
Vous avez
un problème de programmation linéaire . C'est exactement ce que fait Auto Layout avec les contraintes, qui sont non seulement sous forme d'égalités, mais aussi d'inégalités.
Contraintes d'inégalité
Dans le cas des restrictions d'inégalité, la transformation se produit de la même manière que pour les égalités: deux variables supplémentaires sont introduites et tout cela est collecté dans le système. Seule la fonctionnelle est différente, et elle est égale à
a - .

Le graphique ci-dessus montre pourquoi il en est ainsi - toute valeur de
a + avec
a - = 0 (de
X 0 à
+ ∞ ) sera la solution optimale pour le problème.
Essayons de combiner ces deux restrictions d'équations et d'inégalités en une seule - parce que les restrictions ne vivent pas isolément, elles sont appliquées ensemble à l'ensemble du système.

Pour chaque contrainte, une paire de variables supplémentaires est introduite et la fonction est compilée. Puisque nous voulons que toutes ces restrictions soient remplies simultanément, la
fonctionnelle sera égale à la somme de toutes les fonctionnelles de chaque restriction .
Nous collectons la fonction f et voyons que la solution est
X 1 . Comme nous nous y attendions, faire des restrictions. Nous arrivons donc au troisième algorithme.
Algorithme n ° 3
Pour faire quelque chose, il faut:
- créer un système de contraintes linéaires;
- le transformer en un problème de programmation linéaire;
- résoudre le problème de toute manière connue, par exemple, la méthode simplex utilisée dans la mise en page automatique;
- appliquer la solution à UIView.
Cet algorithme semble suffisant, mais considérons le cas suivant: on change l'ensemble initial de contraintes pour que la deuxième contrainte soit maintenant
X ≥ X 2 .

Quelle solution attendons-nous?
- X 1 ? En effet, dans la première restriction, il s'écrit ainsi: X = X 1 , et cette solution entre en conflit avec la deuxième restriction.
- X 2 ? Il y aura déjà un conflit avec la première restriction.
Pour sortir de la situation, nous allons effectuer des transformations que nous savons déjà faire.
Le graphique de la nouvelle fonctionnalité est différent: tout point de l'intervalle de
X 1 à
X 2 sera la bonne solution valide du système. C'est ce qu'on appelle l'
incertitude .
Incertitude
La disposition automatique a un mécanisme pour résoudre ces problèmes - les
priorités . Je vous rappelle que le jaune indique une priorité élevée et le bleu - faible.
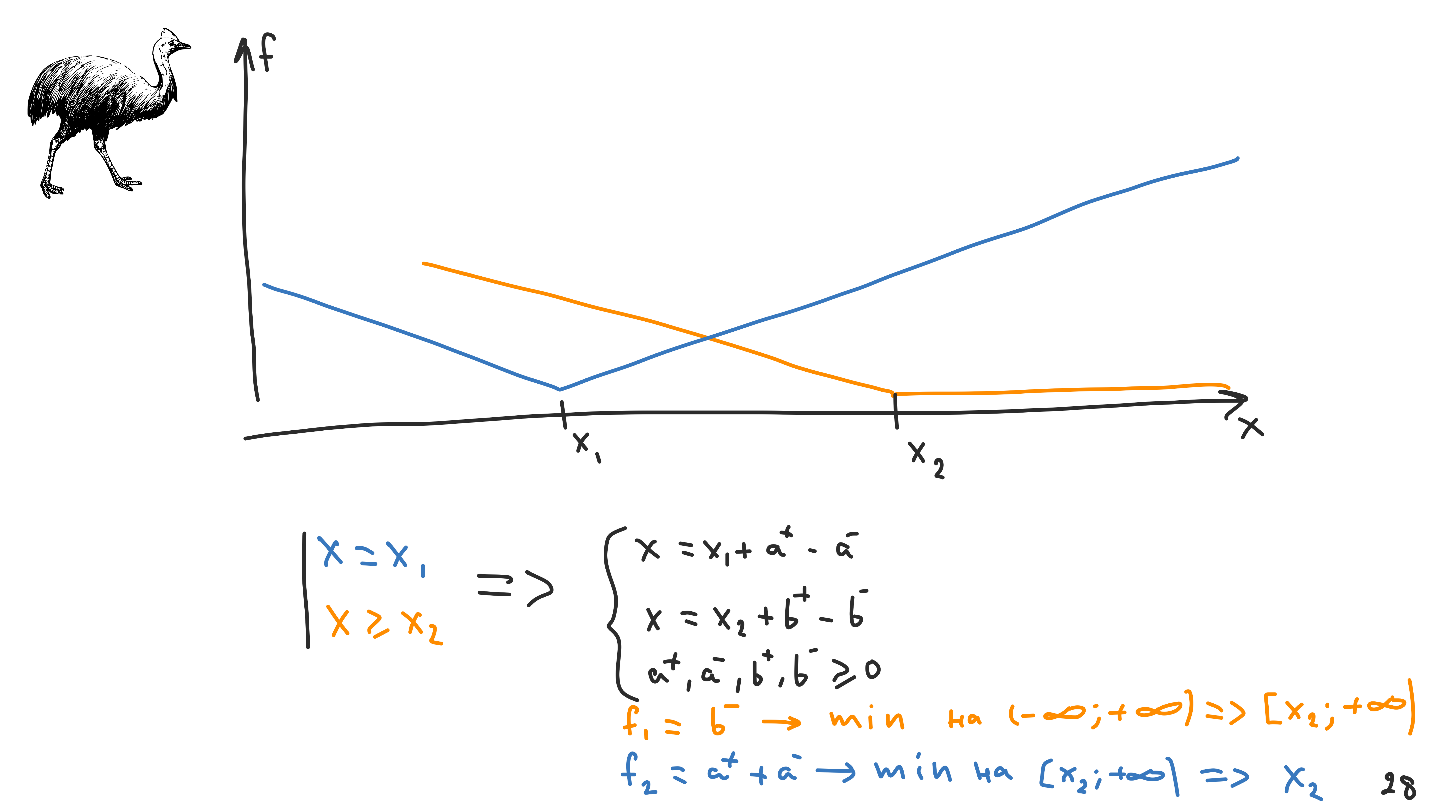
Convertir les restrictions. Veuillez noter que le système résultant est simplement noir. Nous savons comment travailler avec, et il n'y a aucune information sur les restrictions. C'est dans les fonctionnalités, dont il y en aura deux. La disposition automatique réduira d'abord le premier, puis le second.
Dans les problèmes de programmation linéaire, nous ne recherchons pas la solution elle-même, mais la gamme de solutions réalisables. Bien sûr, nous voulons que cette zone ne soit qu'un seul point, et la mise en page automatique agit de la même manière. Premièrement, il minimise la fonction la plus prioritaire sur (
- ∞, + ∞) et, en sortie, reçoit un domaine de solutions réalisables. La disposition automatique résout déjà le deuxième problème de programmation linéaire sur la plage obtenue de valeurs admissibles. Un tel mécanisme est appelé une
hiérarchie de contraintes , et dans ce problème donne le point
X 2 .
Algorithme n ° 4
- Créez une hiérarchie de contraintes linéaires;
- le transformer en tâche de programmation linéaire;
- résoudre séquentiellement le problème de programmation linéaire - de la priorité la plus élevée à la priorité la plus faible.
- appliquer la solution à UlView.
Reprenons la tâche précédente. Nous ne sommes pas des mathématiciens, mais des ingénieurs, et tout ingénieur doit être confondu ici.
Il y a un grave problème ici - l'
infini , et je ne sais pas ce que c'est.
L'algorithme Cassowary sous le capot de la mise en page automatique n'était pas un mécanisme existant qui tombait commodément sur la tâche de mise en page automatique, mais a été pensé comme un outil de mise en page, et il a fourni des mécanismes spéciaux pour échapper à l'infini au tout début. Pour cela, plusieurs types de restrictions ont été inventés:
- Les paramètres sont les contraintes avec lesquelles nous avons travaillé. Elles sont appelées préférences dans l'original , parfois dans la documentation Apple - contraintes facultatives .
- Exigences ou exigences - restrictions avec priorité requises .
Voyons comment les exigences avec de telles priorités sont transformées du point de vue des mathématiques.

Nous avons à nouveau une ligne droite avec deux points, et la première restriction est
X = X 1 . Sur la diapositive, elle est rouge, c'est-à-dire cette restriction avec la priorité requise - nous l'appellerons une exigence.
La disposition automatique la convertit en un système d'équations linéaires contenant une équation
X = X 1 . Rien de plus - pas de tâches de programmation linéaire, pas d'optimisations.
La situation est similaire avec les inégalités, mais un peu plus compliquée -
une variable supplémentaire apparaîtra qui peut prendre toutes les valeurs supérieures à 0. Pour toute valeur supérieure à 0, cette restriction sera satisfaite. Veuillez noter qu'ici, il n'y a pas de tâches de programmation linéaire et d'optimisations.
Essayons de combiner tout cela ensemble, de réunir deux exigences et de les convertir en un seul système. Un lecteur attentif a noté que nous étions arrivés au même problème que celui avec lequel nous avions commencé - les
exigences devraient être cohérentes .
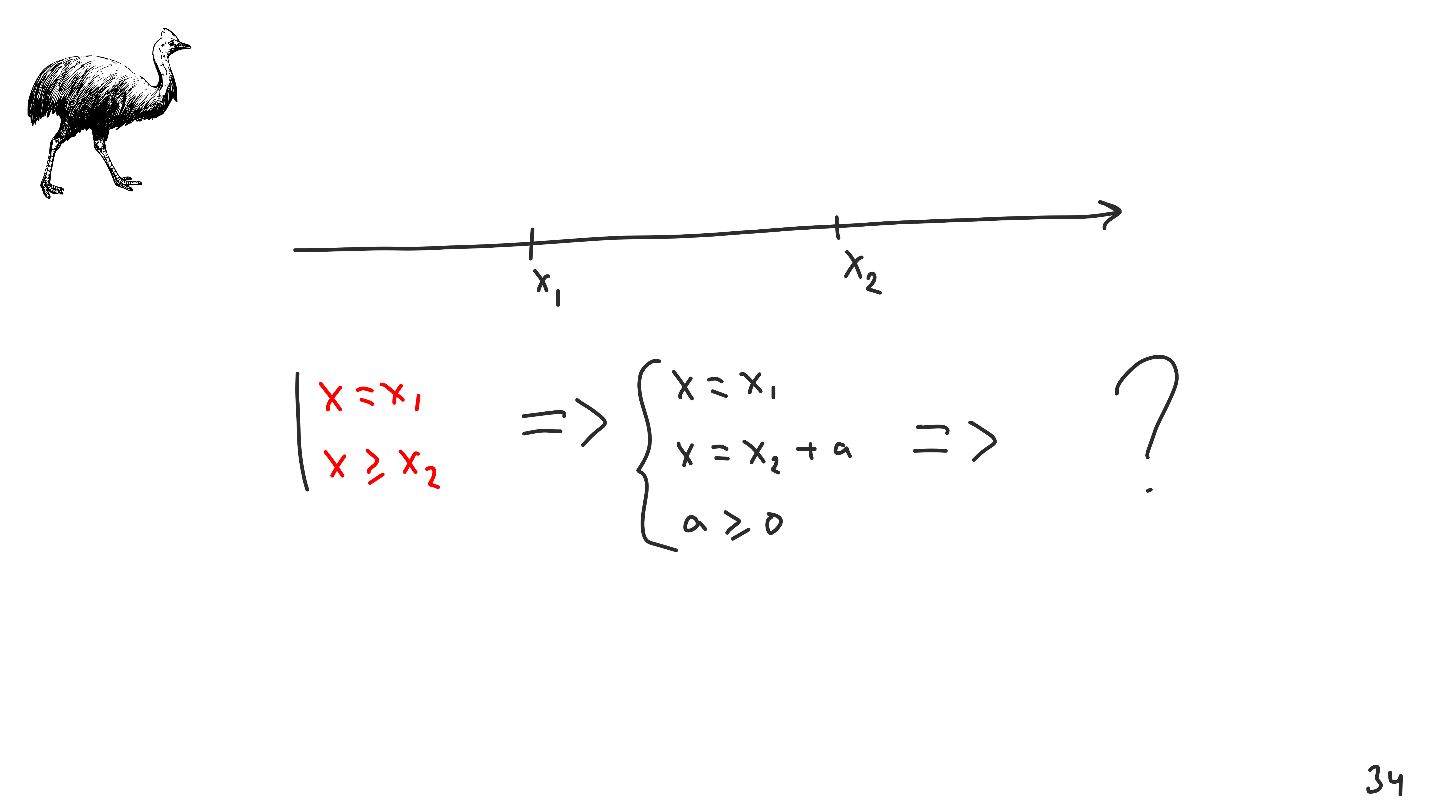
Les contraintes de type
requises ou exigences sont un
outil très puissant, mais pas le principal, mais l'auxiliaire. Il a été spécialement introduit dans Auto Layout pour résoudre le problème des intervalles infinis, il doit être utilisé avec précaution.
Essayons de combiner tous les types de restrictions que nous avons rencontrées dans un seul système. Supposons que nous voulons résoudre le problème non pas sur toute la ligne, mais seulement entre
X 0 et
X 3 . En transformant tout cela en un système d'équations et d'inégalités linéaires, nous obtenons ce qui suit.
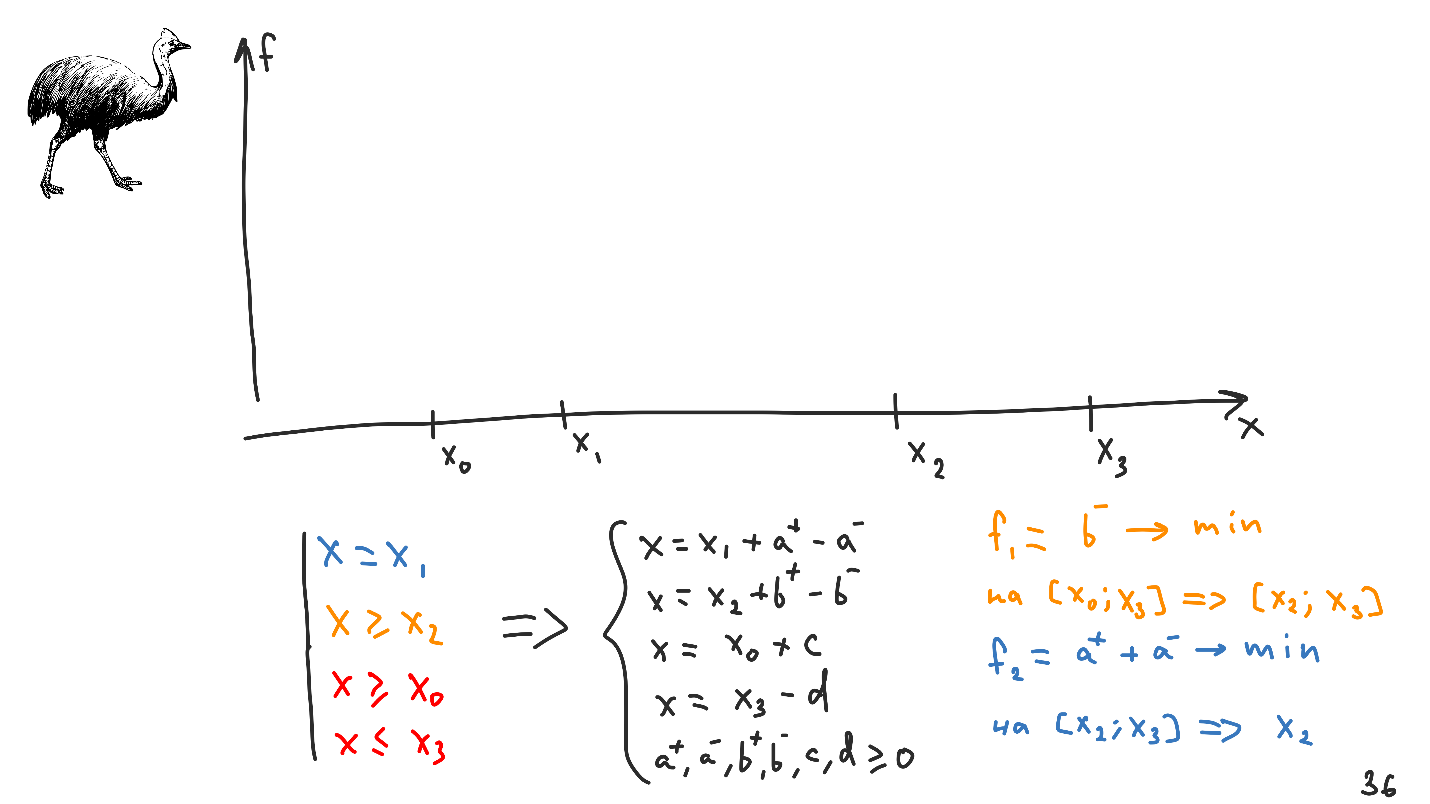
Par rapport au système précédent, deux variables supplémentaires ont été ajoutées -
c et
d , mais elles n'entreront pas dans les fonctionnelles, car les restrictions du type requis n'affectent pas la fonctionnelle dans sa forme d'origine.
Il semble que la tâche n'ait pas beaucoup changé - nous minimisons les mêmes qu'auparavant, mais la plage initiale de valeurs acceptables change, maintenant elle passe de
X 0 à
X 3 .
D'un point de vue mathématique, les exigences - restrictions du type requis - sont la capacité d'introduire des équations supplémentaires dans le système sans modifier ses fonctions.
Vous devez être très prudent avec cela, car un abus excessif des contraintes requises entraînera un
problème sans solutions et la mise en page automatique ne le résoudra pas.
Nous arrivons au dernier cinquième algorithme.
Algorithme n ° 5
- Définir les restrictions nécessaires - les exigences de mise en page;
- créer une hiérarchie de contraintes linéaires;
- convertir toutes les contraintes en un problème de programmation linéaire;
- résoudre le problème de la programmation linéaire;
- appliquer la solution à UlView.
Nous avons examiné Cassowary - un algorithme qui est à l'intérieur de la mise en page automatique, mais quand il est implémenté, diverses fonctionnalités apparaissent.
Fonctionnalités IOS
Il n'y a aucun calcul dans layoutSubviews () .
Quand sont-ils produits? Réponse: toujours, à tout moment la mise en page automatique est comptée. Le calcul se produit exactement lorsque nous ajoutons des contraintes à notre vue ou les activons à l'aide de méthodes API modernes pour travailler avec des contraintes.
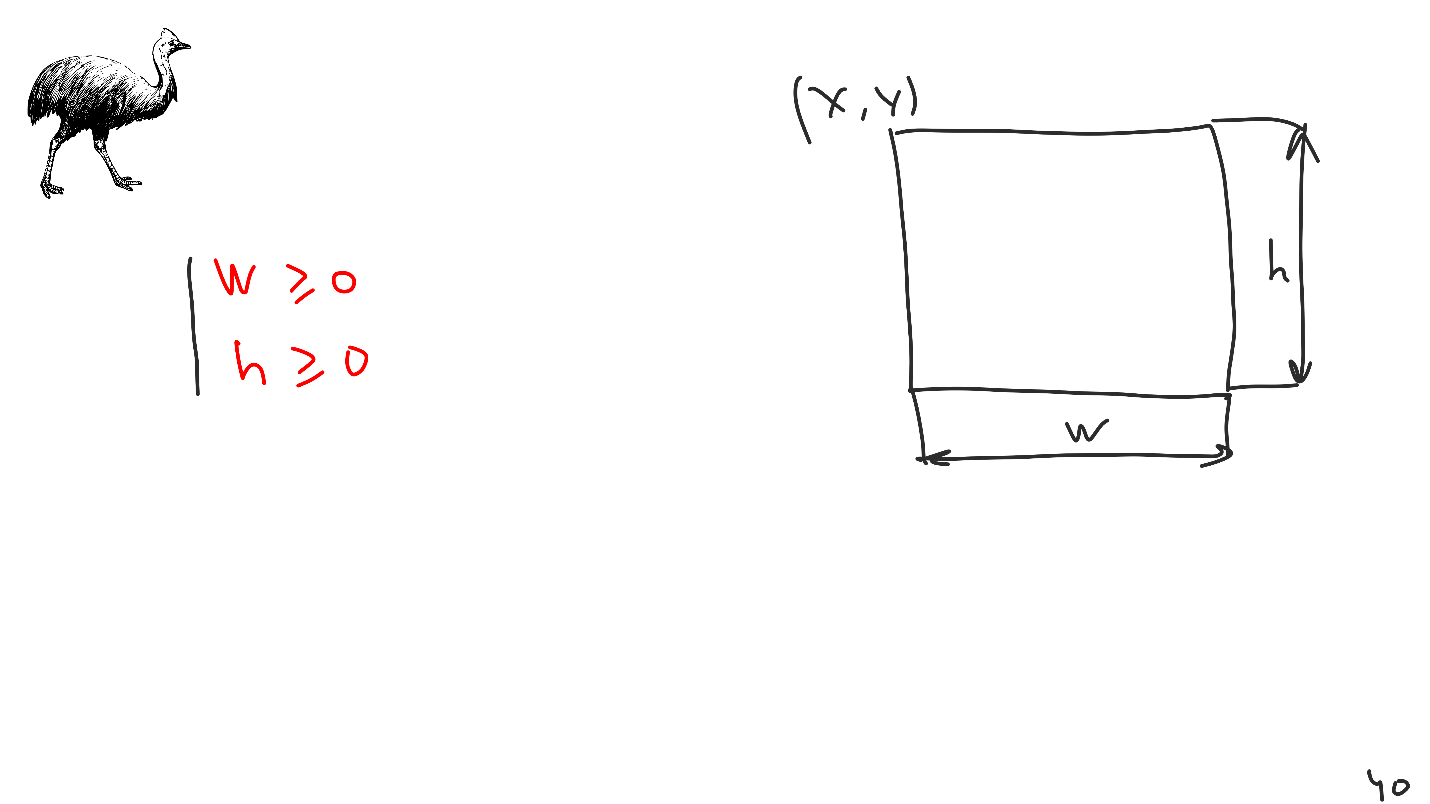
Nos vues sont des rectangles, mais le problème est que ces informations ne sont pas contenues dans le casoar, elles doivent y être en outre intégrées. Nous avons un mécanisme pour introduire des restrictions supplémentaires. Si nous introduisons pour chaque vue un ensemble de contraintes avec une largeur et une hauteur positives, alors nous aurons toujours des rectangles à la sortie. C'est pourquoi nous ne pouvons pas rattraper la vue Disposition automatique avec des dimensions négatives.
La deuxième caractéristique est
intrinsicContentSize - la taille intrinsèque qui peut être définie pour chaque vue.
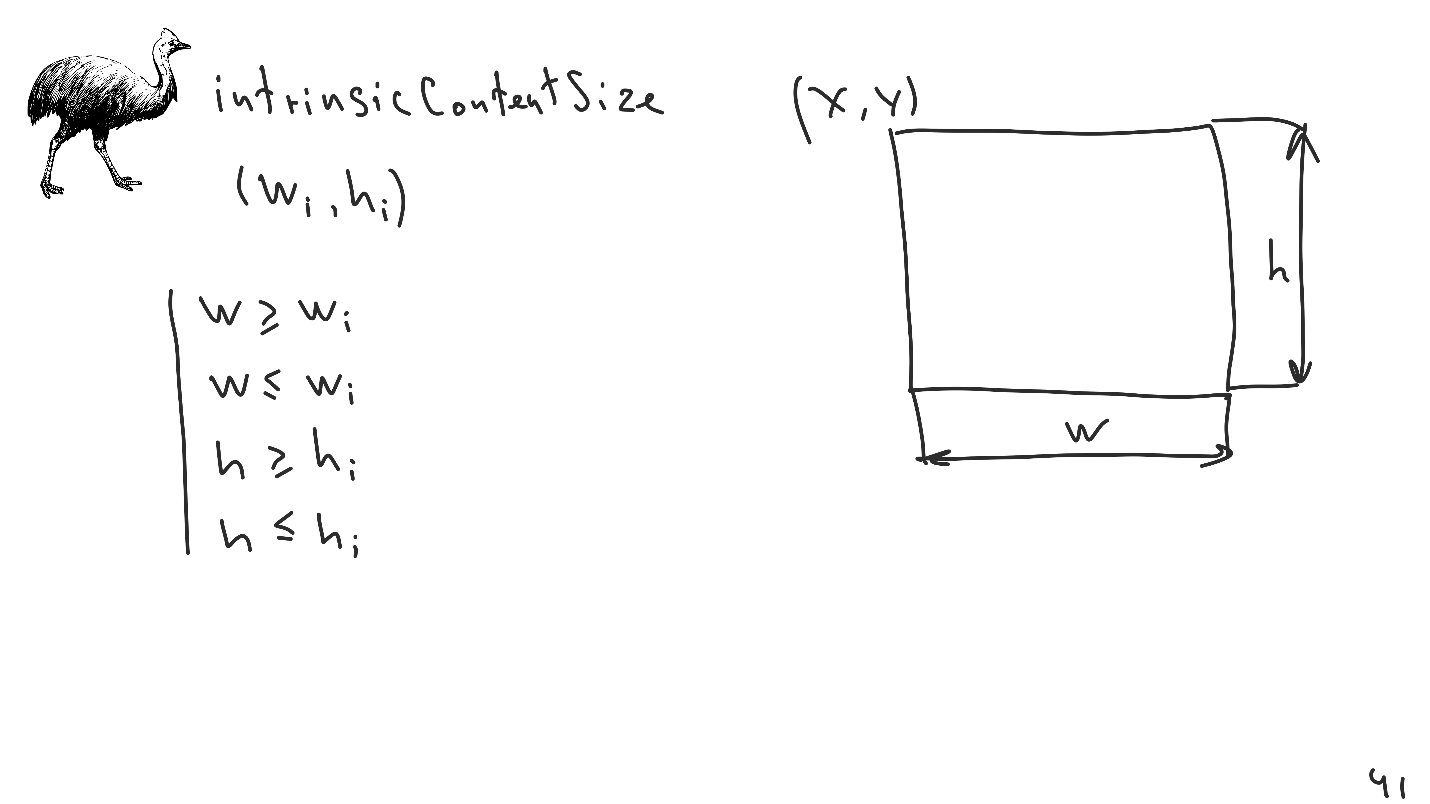
Il s'agit d'une interface simple pour créer 4 contraintes d'inégalité supplémentaires qui seront placées dans le système. Ce mécanisme est très pratique, il vous permet de réduire le nombre de restrictions explicites, ce qui simplifie l'utilisation de la mise en page automatique. Le dernier et le plus fin point qui est souvent oublié est
TranslateAutoresizingMaskIntoConstraints.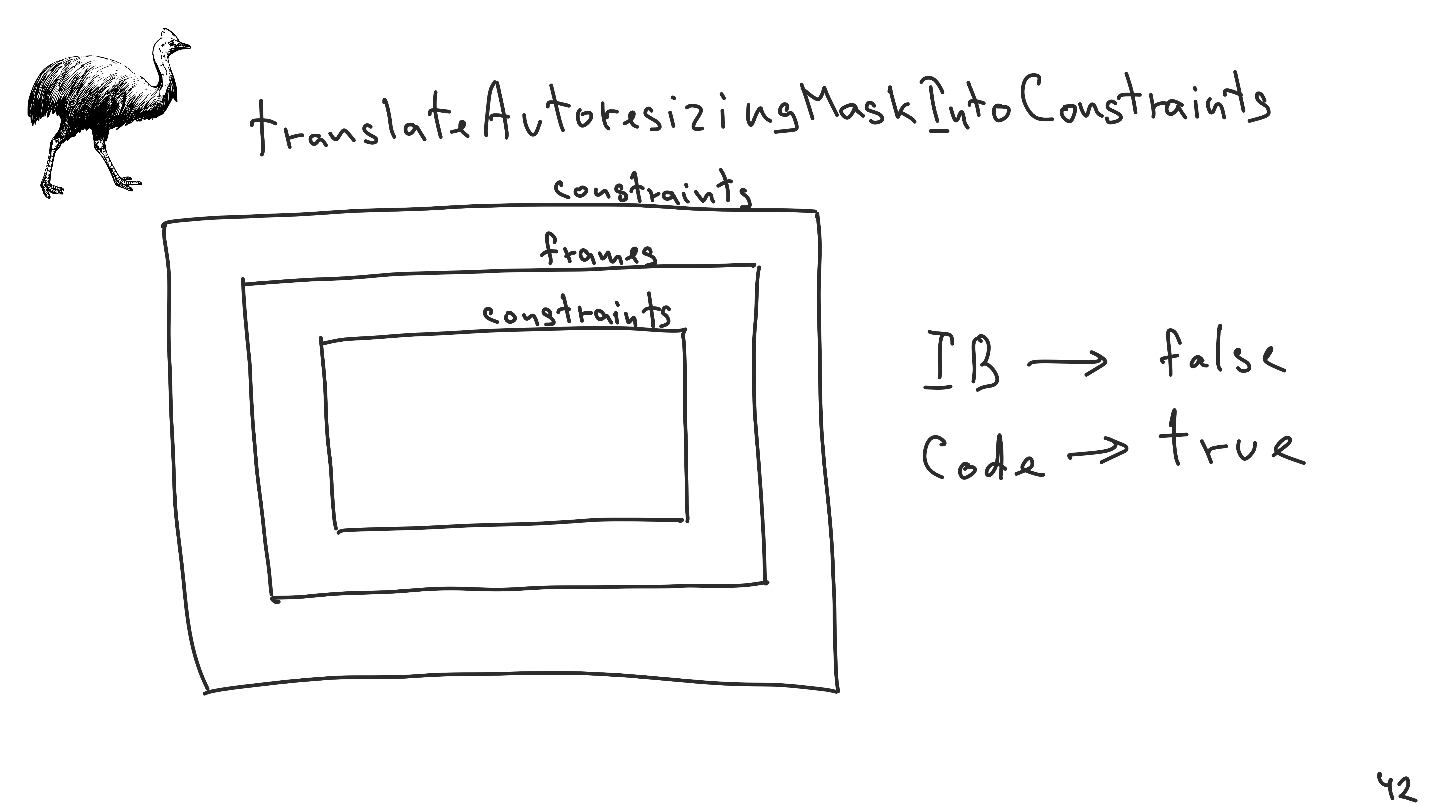
Il s'agit d'une
béquille qui a été introduite à l'époque d'iOS 5, afin que l'ancien code ne se casse pas après l'apparition de la mise en page automatique.
Imaginez une situation: nous imposons une vue sur les contraintes. À l'intérieur de la vue, nous utilisons la vue, qui ne connaît rien aux contraintes, tout se compose sur les cadres, mais à l'intérieur, elle tape la vue, qui a longtemps été traduite en contraintes.
Je vous rappelle qu'aucun cadre n'entre dans la tâche de mise en page automatique de Cassowary, seulement des limitations.
La taille et la position de la vue réduite sur les images ne sont pas entièrement déterminées par des contraintes. Lors du calcul de la taille et de la position de toutes les autres vues, les tailles incorrectes seront prises en compte, même si après la mise en page automatique, nous y appliquerons les cadres corrects.
Pour éviter cette situation, si la valeur de la variable TranslateAutoresizingMaskIntoConstraints est vraie, une restriction supplémentaire est appliquée à chaque vue disposée sur le cadre. Cet ensemble de restrictions peut varier d'une exécution à l'autre. Une seule chose est connue sur cet ensemble - sa trame sera celle qui a été transmise.
La compatibilité entre l'ancien code écrit sans contraintes et le nouveau code écrit avec des contraintes peut souvent souffrir en raison d'une mauvaise utilisation de cette propriété. Ces restrictions ont nécessairement la priorité des exigences, donc si nous imposons soudainement une contrainte à une telle vue, qui a une priorité très élevée, par exemple une exigence, nous pouvons accidentellement créer un système non cohérent qui n'aura pas de solutions.
Il est important de savoir:- Si nous créons une vue depuis Interface Builder , la valeur par défaut de cette propriété sera false .
- Si nous créons une vue directement à partir du code, ce sera vrai .
L'idée est très simple - l'ancien code dans lequel la vue a été créée ne savait rien de la disposition automatique, et il était nécessaire de faire en sorte que si la vue était utilisée quelque part dans un nouvel endroit, cela fonctionnerait.
Conseils pratiques
Il y aura trois conseils en tout et commencer par le plus important.
Optimisation
Il est important de localiser le problème.
Avez-vous déjà rencontré le problème de l'optimisation de l'écran, qui est présenté sur la disposition automatique? Probablement pas, vous avez plus souvent rencontré le problème de l'optimisation de la disposition des cellules à l'intérieur d'un tableau ou d'une
vue de collection .
La disposition automatique est suffisamment optimisée pour créer n'importe quel écran et n'importe quelle interface, mais en faire 50 ou 100 à la fois est un problème pour elle. Pour le localiser et l'optimiser, regardons l'expérience. Les chiffres sont tirés d'un
article où Cassowary a été décrit pour la première fois.

La tâche est la suivante: nous créons une chaîne de vues une par une, et nous connectons chaque chaîne suivante à la précédente. Ainsi, une séquence de 1000 éléments a été construite. Après avoir mesuré diverses opérations, le temps est indiqué en millisecondes. Les valeurs sont assez grandes, car la disposition automatique a été inventée à la jonction des années 80 et 90.
En collectant une telle chaîne, vous pouvez agir comme suit:
- Ajoutez une contrainte à la fois et décidez à chaque fois. Cela prendra 38 secondes.
- Vous pouvez ajouter toutes les restrictions à la fois , puis résoudre le système uniquement. Cette solution est plus efficace. Selon les anciennes données, l'efficacité augmente de 70%, mais dans la mise en œuvre actuelle sur les appareils modernes, il n'y aura que 20%. Mais un ajout qualitativement ponctuel de restrictions sera toujours plus efficace.
- Lorsque toute la chaîne est assemblée, vous pouvez ajouter une restriction supplémentaire . Comme le montre le tableau, cette opération est assez bon marché.
- La chose la plus intéressante: si nous n'ajoutons aucune nouvelle restriction, mais changeons une constante dans l'une des restrictions existantes , c'est un ordre de grandeur plus efficace que la suppression ou la création d'une nouvelle restriction.
Les deux premiers points peuvent être décrits comme le calcul principal des interfaces, les deux derniers - comme le suivant.
Calcul de l'interface principale
Ici, vous pouvez utiliser les méthodes d'ajout en masse de contraintes pour l'optimisation:
- NSLayoutConstraints.activate (_ :) - lors de la création d'une vue, collectez toutes les contraintes de manière séquentielle dans un tableau, mettez en cache et ajoutez-les ensuite à la fois.
- Ou créez des cellules dans Interface Builder. Il fera tout pour nous et procédera à une optimisation supplémentaire, ce qui est souvent pratique.
Calculs d'interface ultérieurs
L'ajout ou la modification d'une contrainte est une opération complexe. Il est donc préférable de
ne pas modifier l'ensemble de contraintes, mais uniquement de modifier les constantes des contraintes existantes. :
- UIView — . view , Auto Layout. , , view, .
- — IntrinsicContentSize. , , .
- . , , .
,
WWDC 2018S220 High Performance Auto Layout . — Apple , .
, constraints.
required , — , , . .
, .
:
, , .
constraint required, . , , , . , .
—
, . , — . - , , . Auto Layout , .
, . . , , , . layout, , , . .
— , Auto Layout, , .
, required, ,
. :
, ,
, .
, . , , , . ,
— . .
— . , , , — , — required -.
Liens utiles:Résolution des contraintes arithmétiques linéaires pour les applications d'interface utilisateurLa contrainte linéaire Cassowary Résoudre les contraintes de l'algorithme entant que modèle de conceptionGuide de mise en page automatique par AppleWWDC 2018 Session 220 Disposition automatique haute performanceMagic UILabel ou mise en page automatique de l'API privée - Alexander GoremykinMedium Blog Yandex.MapSoit dit en passant, nous avons déjà accepté le rapport d'Anton dans le programme AppsConf 2019 . Permettez-moi de vous rappeler que nous avons déplacé AppsConf de l'automne au printemps, et la prochaine conférence la plus utile pour les développeurs mobiles se tiendra les 22 et 23 avril. Il est temps de réfléchir au sujet de présentation et de soumettre un rapport , ou de discuter avec le chef de file de l'importance d'aller à la conférence et de réserver un billet.