🤰🏻 🚷 😝 Histoire de Shipastik 📿 👢 👩🏾‍🌾

Des pointes partout

Nous l'appelons Spikey, et dans ma vie aujourd'hui je le rencontre constamment:

Il provient d'un objet tridimensionnel, un polyèdre appelé «rhombique soixantième».

Mais quelle est son histoire et pourquoi en avons-nous fait notre symbole?

L'origine de Thorn

En 1987, lorsque nous développions la première version de Mathematica, l'une de ses innovations était la possibilité de générer des graphiques tridimensionnels indépendants de la résolution basés sur des descriptions symboliques. Dans les premières démonstrations, cela nous a permis de produire des images étonnamment claires de polyèdres réguliers. Mais, à l'approche de la sortie de Mathematica 1.0, nous voulions utiliser un exemple plus impressionnant. Par conséquent, nous avons décidé de prendre le dernier polyèdre ordinaire - l' icosaèdre - et d'en faire quelque chose de plus complexe en lui donnant une forme d'étoile, ou, plus correctement, un cumul. Oui, voilà à quoi ressemblait la première interface de portable il y a 30 ans.

Au début, c'était juste une belle démonstration qui a fonctionné assez rapidement sur nos ordinateurs de l'époque. Mais bientôt l'objet tridimensionnel généré par lui a commencé à être de facto utilisé comme logo pour Mathematica. Et au moment où la version 1.0 est sortie en 1988, l'icosaèdre étoilé était partout:

Au fil du temps, diverses dédicaces à notre polyèdre stellaire ont commencé à apparaître - faites dans différents matériaux et tailles:

Mais, un an seulement après la sortie de Mathematica 1.0, nous étions prêts à publier Mathematica 1.2, et pour transmettre la complexité du produit, nous avions besoin d'un logo sophistiqué. Un de nos développeurs, Igor Rivin, a soutenu sa thèse de doctorat sur les polyèdres dans l'espace hyperbolique - et grâce à ses efforts, les matériaux de la version 1.2 ont été décorés d'un icosaèdre hyperbolique:

Mes employés m'ont donné un T-shirt avec Shipastik alors moderne pour mon 30e anniversaire en 1989, et une citation que je soutiens même après tant d'années:

«La compagnie est amusante»

Après la sortie de Mathematica 1.2, dans nos supports marketing, on pouvait trouver toute une collection de polyèdres hyperboliques réguliers, mais avec l'avènement de la version 2.0 en 1991, nous avons décidé que nous aimions le plus l'icosaèdre hyperbolique:

Mais nous avons continué à explorer d'autres formes enrichies. Inspiré par le dessin de Léonard de Vinci d'un «modèle en bois» de l'icosaèdre étoilé (réalisé avec une perspective étonnamment précise) pour le livre de Luke Pacioli «On Divine Proportion», nous avons commandé une affiche de la version 2.0 où cinq tétraèdres qui se croisent sont disposés de sorte que leurs sommets extérieurs forment le dodécaèdre:

Aujourd'hui, en parcourant mes archives de 1991, je trouve le code «explicatif», et c'est agréable de voir qu'il s'exécute facilement dans notre dernière version de Wolfram Language (bien qu'aujourd'hui il puisse être écrit un peu plus élégamment):

Au fil des ans, cela est devenu un étrange rituel - en préparation du lancement de la prochaine version principale de Mathematica, nous organiserons des réunions sérieuses où nous nous engageons à «choisir un nouveau Shipastik». Parfois, vous devez choisir parmi des centaines d'options différentes créées à l'aide d'algorithmes complètement différents:

Mais, bien que les palettes de couleurs soient en mutation, et les Shipastiks reflètent souvent la présence de nouvelles fonctionnalités dans le système (quoique quelque peu implicitement), nous avons une tradition de 30 ans de choix des options pour un dodécaèdre hyperbolique:

Récemment, il est devenu courant d'étudier l'espace paramétrique - bien que nous ayons déjà accumulé des centaines de paramètres:

Le dodécaèdre hyperbolique a 20 pics - il était idéal pour célébrer le 20e anniversaire de Mathematica en 2008. Mais lorsque nous avons voulu faire quelque chose de similaire pour le 25e anniversaire en 2013, nous avons été confrontés au problème du manque de polyèdres réguliers à 25 sommets. Mais (en fait, en utilisant la fonction SpherePoints [25]), nous avons pu créer un chiffre approximatif et l'imprimer sur une imprimante 3D pour tous les employés de l'entreprise, avec des tailles correspondant à l'ancienneté des employés.

Quitter Wolfram | Alpha

En 2009, nous nous préparions pour la sortie de Wolfram | Alpha, et le système avait besoin d'un logo. Il y avait de nombreux concepts:

Nous voulions souligner que Wolfram | Alpha fonctionne au moyen de calculs et non pas, par exemple, comme moteur de recherche. Et depuis quelque temps, nous voulions utiliser quelque chose avec des engrenages. Mais nous voulions également que le logo ressemble au logo Mathematica de longue date. Cela a donné lieu à l'un de ces projets tels que «notre général est devenu fou»: la création d'un mécanisme d'engrenage à partir de formes à pointes.

Un utilisateur de longue date de Mathematica et Wolfram Language, un ingénieur en mécanique hongrois, Sandor Kabai, nous a aidés en proposant des «engrenages à pointes»:

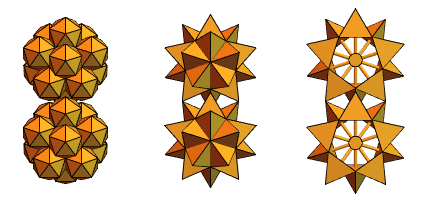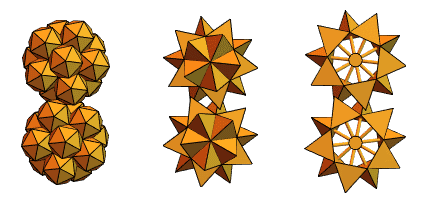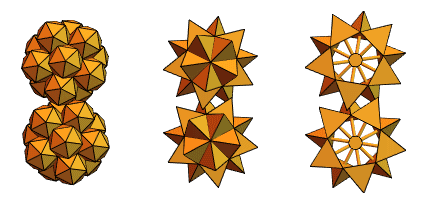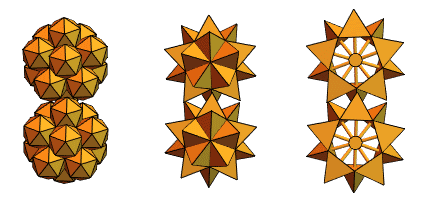
Revenant aux tétraèdres entrecroisés de la version 2, il a créé quelque chose comme ceci:

En 2009, les imprimantes 3D sont devenues très populaires, et nous avons pensé qu'il serait bien de créer un logo pour Wolfram | Alpha qui pourrait être imprimé. Le polyèdre hyperbolique ne convenait pas - les pointes pourraient se rompre et constituer une menace. Des formes comme des pointes de la 4e version, avec des "pointes sûres", manquaient d'élégance.

Pendant un certain temps, nous nous sommes accrochés à une idée avec des engrenages. Mais à la fin, ils ont décidé qu'il valait la peine de revoir les polyèdres ordinaires. Mais quel polyèdre pouvons-nous choisir?

Bien sûr, il existe un nombre infini de polyèdres possibles. Mais pour notre logo, nous voulions choisir un polyèdre symétrique et, dans une certaine mesure, «droit». Cinq polyèdres réguliers (ou «solides platoniciens») - dont les faces sont les mêmes polygones réguliers - peuvent être considérés comme les «plus réguliers» de tous:

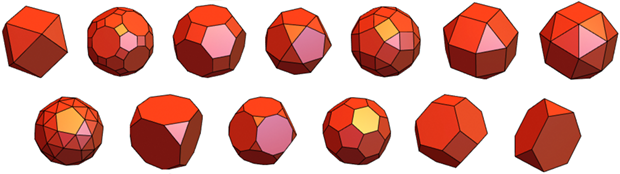
Il existe 13 autres corps archimédiens - ils ont des sommets identiques et des polygones réguliers, bien que de types différents, agissent comme des faces:

Il existe de nombreux types de «correction» des polyèdres. Un exemple en est le «polyèdre homogène» qu'une affiche du Mathematica Journal de 1993 montre:

Au cours des années où Eric Weinstein a collecté la collection, qui en 1999 était devenue MathWorld, il a essayé d'inclure des articles sur autant de polygones que possible. En 2006, dans le cadre de l'inclusion de diverses données systématisées dans Mathematica et Wolfram Language, nous avons commencé à inclure des données de polygones avec MathWorld. En conséquence, après la sortie de la version 6.0 en 2007, la fonction PolyhedronData est apparue, qui contenait des données complètes sur 187 polygones remarquables:

Dans Mathematica et Wolfram Language, vous pouviez toujours générer des polygones réguliers, mais maintenant c'est devenu plus facile à faire. Avec la version 6.0, nous avons également publié le Wolfram Demonstrations Project, qui a rapidement commencé à se reconstituer avec diverses démos liées aux polyèdres.

L'un d'eux a été réalisé par ma fille Katerina à l'âge de 10 ans (elle continue aujourd'hui de se développer dans les domaines de la géométrie): ce sont des «koalas polyédriques», décomposés par tous les polyèdres de PolyhedronData [] utilisés:

Dans un tel contexte, nous avons voulu en 2009 «choisir un polyèdre» pour Wolfram | Alpha. Tout a été décidé le vendredi 6 février, lorsque je me suis mis au travail par moi-même.

J'ai conservé ce cahier, et cela montre que j'ai d'abord essayé de mettre en œuvre l'idée douteuse de placer des sphères aux sommets des polyèdres:

Mais, comme enregistré dans le carnet d'histoire , deux minutes plus tard, je suis passé à des polyèdres purs - ils étaient tous orange, que nous voulions ensuite utiliser pour le logo:

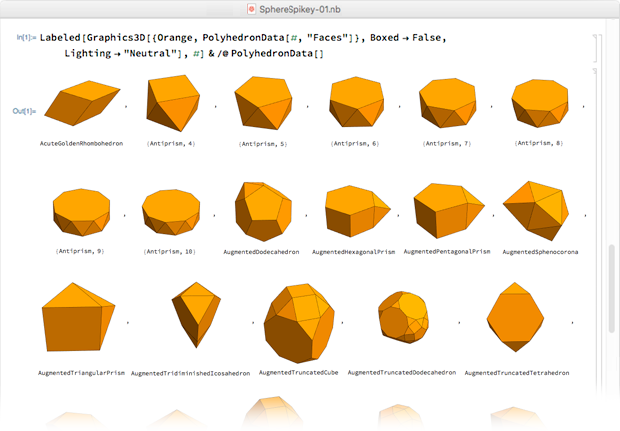
Les polyèdres ont été classés par ordre alphabétique par nom, et sur la 28e ligne, il est apparu - un hexaèdre rhombique.

Quelques minutes plus tard, à 7 h 24 min 24 s, le 7 février 2009, j'ai découvert cet hexaèdre rhombique et je l'ai transformé en une position symétrique, que nous utilisons maintenant:

Je voulais voir à quoi cela ressemblerait en gris et en silhouette, et quatre minutes plus tard, j'ai utilisé ColorSeparate pour découvrir:

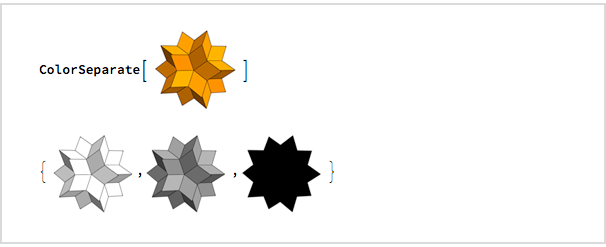
J'ai immédiatement commencé à écrire un e-mail, que j'ai envoyé à 00:32:

J'aime vraiment RhombicHexecontahedron. Il a une forme intéressante et très symétrique. Il me semble que sa précision nous convient, et la silhouette semble assez raisonnable.

Évidemment, je viens de copier RhombicHexecontahedron du cahier (je doute que j'aurais pu écrire l'hexagone [hexecontaèdre] sans erreur). D'après mes archives, je sais que c'était la première fois que j'écrivais le nom du polyèdre, qui est destiné à devenir mon préféré.

Dans Wolfram Language, il était très facile d'obtenir une image d'un hexaèdre rhombique et de jouer avec:

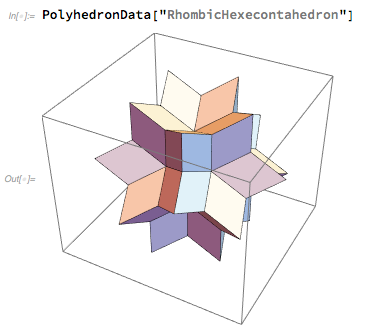
Lundi, il était clair que l'hexaèdre rhombique avait gagné - et notre service visuel était occupé à le rédiger en tant que logo pour Wolfram | Alpha. Nous en avons essayé différentes orientations, mais finalement nous nous sommes installés sur la position symétrique «en pleine vue» que j'ai choisie. (Nous devions également choisir la meilleure «distance focale» pour l'angle le plus approprié).

Comme notre icosaèdre étoilé de la version 1.0, l'hexaèdre rhombique a 60 faces. Mais d'une manière ou d'une autre, grâce aux combinaisons «cinq pétales», il a l'air beaucoup plus élégant. Beaucoup d'efforts ont été consacrés au choix d'un tel ombrage des visages afin que le dessin en deux dimensions reflète correctement l'objet en trois dimensions. Mais nous avons bientôt introduit la première version officielle de notre logo:

Elle a rapidement commencé à apparaître partout, et, en hommage à nos premières idées, souvent sur un fond orné d'engrenages:

Quelques années plus tard, nous avons légèrement corrigé l'ombrage des bords, ce qui a conduit à la création du logo Wolfram | Alpha, toujours utilisé:

Hexagone rhombique

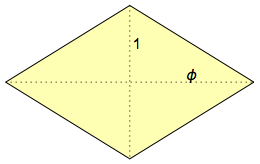
Qu'est-ce qu'un hexaèdre rhombique? En anglais, il est appelé hexécontaèdre, car il a 60 faces, et ἑξηκοντα (hexekont) est le mot grec pour «60». Ses visages sont des losanges dorés , qui sont nommés ainsi parce que leurs diagonales sont liées les unes aux autres selon le nombre d'or: φ = (1 + √5) / 2 & sime; 1,618:

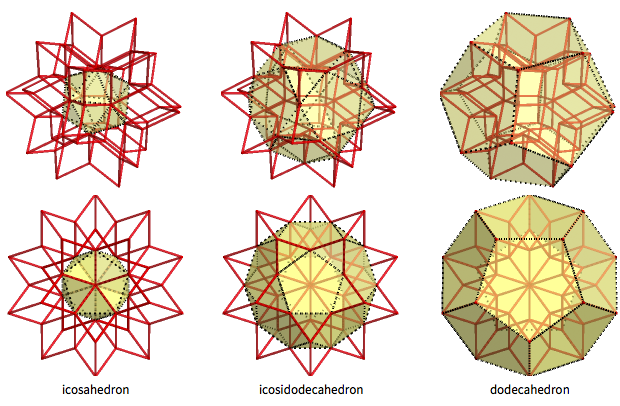
L'hexaèdre rhombique est un corps intermédiaire intéressant entre l'icosaèdre et le dodécaèdre (avec l'icosododécaèdre entre eux). Les 12 sommets intérieurs de l'hexaèdre rhombique forment l'icosaèdre régulier et les 20 sommets extérieurs forment le dodécaèdre régulier. 30 «pics intermédiaires» forment l'icosododécaèdre à 32 facettes (il a 20 faces triangulaires et 12 pentagonales):

Au total, l'hexaèdre rhombique a 62 sommets et 120 arêtes (ainsi que 120-62 + 2 = 60 faces). Il a trois types de sommets ("interne", "moyen" et "externe") correspondant à 12 + 30 + 20 sommets de l'icosaèdre, de l'icosododécaèdre et du dodécaèdre. À ces sommets, les arêtes 3, 4 et 5 convergent respectivement. Chaque face a un sommet «interne» où 5 arêtes se rencontrent, un sommet externe où trois arêtes se rencontrent et deux «intermédiaires» où 4 arêtes se rencontrent. Les sommets extérieur et intérieur sont les sommets à angle aigu des losanges dorés, et les sommets intermédiaires sont à angle obtus.

L'angle aux pics pointus des losanges dorés est de 2 tan ^-1 (φ ^-1 ) ≈ 63,43 °, et aux pics pointus est de 2 tan ^-1 (φ) ≈ 116,57 °. De tels angles vous permettent d'assembler un hexaèdre rhombique du constructeur Zometool en utilisant uniquement les supports rouges (comme dans le cas du dodécaèdre):

Sur 120 arêtes de l'hexaèdre rhombique de 60 «charnières internes», l'angle dièdre est de 4π / 5 = 144 °, et pour 60 externes il est de 2π / 5 = 72 °. Les angles contractés par les sommets extérieur et intérieur sont π / 5 et 3π / 5.

Pour dessiner un hexaèdre rhombique, vous devez connaître les coordonnées tridimensionnelles de ses sommets. Ils sont facilement obtenus en utilisant le fait que l'hexaèdre rhombique est invariant par rapport au groupe icosaèdre, vous pouvez donc commencer avec un losange doré et simplement ajouter 60 matrices qui forment une représentation tridimensionnelle du groupe icosaèdre. Cela donne, par exemple, les coordonnées finales des sommets en {± φ, ± 1,0}, {± 1, ± φ, ± (1 + φ)}, {± 2φ, 0,0}, {± φ, ± ( 1 + 2φ), 0}, {± (1 + φ), ± (1 + φ), ± (1 + φ)} et leurs permutations cycliques avec tous les signes possibles.

En plus du fait que les faces d'un hexaèdre rhombique sont des losanges dorés, un hexaèdre rhombique peut être construit à partir de 20 rhomboèdres dorés (dans lesquels les six faces sont des losanges dorés):

Il existe d'autres façons de créer un hexaèdre rhombique à partir d'autres polyèdres. Il peut être obtenu à partir de cinq cubes entrecroisés et de 182 dodécaèdres en contact avec les faces:

Vous ne pouvez pas disposer une mosaïque continue de soixante hexaèdres rhombiques, mais ils s'imbriquent bien les uns aux autres (et, oui, j'ai vu des dizaines de Shipastiks en papier se plier de cette façon):

Vous pouvez également en faire toutes sortes d'anneaux et d'autres configurations:

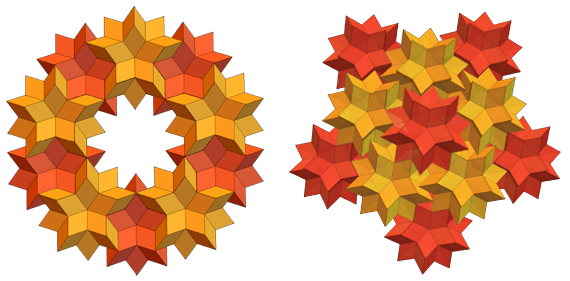
Un proche parent de l'hexaèdre rhombique (RS) est le trente-tétraèdre rhombique (RT). RS et RT ont des visages qui sont des losanges dorés. Mais RS en a 60 et RT en a 30. Voici à quoi ressemble une RT distincte:

Plusieurs RT sont parfaitement investis dans les poches RS, et des choses similaires se révèlent:

Sandor Kabay, mentionné précédemment, s'est intéressé aux RSh et RT vers 2002. Et après le lancement du Wolfram Demonstrations Project, lui, avec le mathématicien slovène Isidor Hafner, a ajouté plus d'une centaine de démonstrations au projet liées à RS, RT et à plusieurs de leurs propriétés:

Modèles de papier épineux

Dès que nous avons décidé que Shipastik serait un RS, nous avons commencé à fabriquer ses modèles 3D. Maintenant, il est très simple de le faire en utilisant la fonction Printout3D [PolyhedronData [...]], et des modèles déjà calculés peuvent être trouvés sur des ressources tierces .

En mai 2009, lors du lancement de Wolfram | Alpha, nous avions déjà beaucoup de pointes 3D à portée de main:

Mais, en préparant la première saison des fêtes après cet événement, nous avons décidé de donner à chacun la possibilité de créer son propre Shipastik en trois dimensions. Tout d'abord, nous avons envisagé l'option avec 20 aimants rhomboédriques recouverts de plastique. Mais ils sont sortis chers et ne se sont pas très bien collés.

Cela nous a conduit à l'idée de fabriquer Shipastik à partir de papier ou de carton fin. Par conséquent, au début, nous voulions créer un schéma qui pourrait être intégré à Shipastika:

Ma fille Katerina a servi de testeur (et elle a toujours un échantillon de test), mais il est devenu clair que de nombreuses situations inconfortables apparaissent dans le processus de pliage, dans lesquelles il n'est pas clair comment passer d'une position à une autre. Vous pouvez faire un grand nombre de dispositions (il y en a 43 380 uniquement pour le dodécaèdre et l'icosaèdre) - et nous avons pensé qu'il serait peut-être possible de choisir quelque chose de mieux parmi elles:

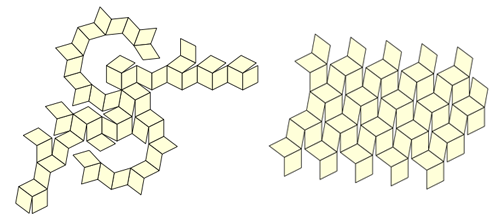
Mais, lorsque nous n'avons pas pu trouver un tel schéma, nous avons eu une idée nouvelle (quoique évidente): si le modèle tenait aux oreilles, pourquoi ne pas le fabriquer en quelques morceaux? Nous avons rapidement réalisé que pour cela, vous ne devez prendre que 12 pièces identiques de ce type:

Avec leur aide, nous avons créé nos " décors de sculptures en papier ":

Une tâche intéressante consistait à rédiger des instructions faciles à comprendre, mais après plusieurs itérations, les instructions sont devenues simples et bien développées:

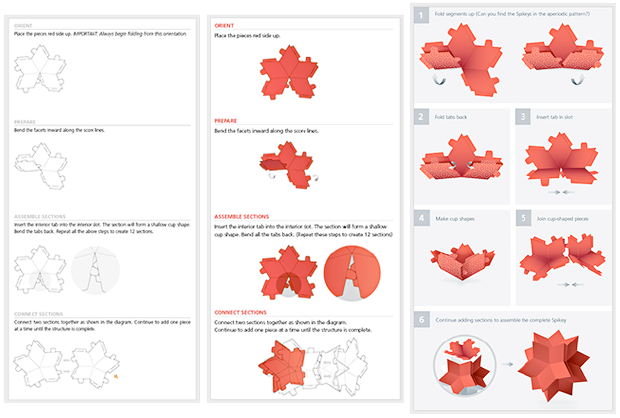
Et après que le papier Shipastiks soit allé aux gens, nos utilisateurs ont commencé à nous envoyer toutes sortes d'images Shipastik «sur le terrain»:

Le chemin vers l'hexagone rhombique

Le cube aux multiples facettes de l'Égypte ancienne

On ne sait pas qui a décrit pour la première fois les solides platoniciens. Peut-être cela a-t-il été fait par les Pythagoriciens (qui vivaient près de tels grands dépôts de cristaux de pyrite à multiples facettes). Peut-être que quelqu'un a fait cela bien avant eux. C'était peut-être un contemporain de Platon, Teetet d'Athènes . Mais, en tout cas, au moment de Platon (vers 400 avant JC), cinq solides platoniciens étaient connus. Et quand Euclide a écrit ses Éléments (vers 300 g av. J.-C.), l'un des piliers de ce travail était la preuve de l'absence d'autres polyèdres réguliers. Cette preuve est connue pour avoir pris le plus grand nombre de pas par rapport aux axiomes euclidiens originaux - 32.

Les solides platoniciens étaient utilisés pour les dés et les ornements. Mais on lui a également attribué un rôle central dans la réflexion sur la nature - par exemple, Platon a suggéré que, dans un sens, tout pourrait être composé d'eux: la terre à partir de cubes, l'air à partir d'octaèdres, l'eau à partir d'icosaèdres, le feu à partir de tétraèdres et le paradis ) des dodécaèdres.

Et les autres polyèdres? Au 4ème siècle après JC Papp d'Alexandrie a écrit que quelques siècles avant qu'Archimède ait découvert 13 autres "polyèdres réguliers" - apparemment, ce qu'on appelle maintenant des corps archimédiens - bien que les détails de cela soient perdus. Et depuis mille ans, peu de choses sont arrivées aux polyèdres. Mais au XVe siècle, avec le début de la Renaissance, les polyèdres redeviennent à la mode. Leonardo da Vinci et Albrecht Dürer les ont régulièrement utilisés dans l'art et le design, redécouvrant certains des corps archimédiens - ainsi que la découverte de nouveaux polyèdres, par exemple l'icodosodécaèdre.

Mais le plus grand pas en avant pour les polyèdres a été l' œuvre de Johannes Kepler au début du XVIIe siècle. Tout a commencé avec une théorie élégante, quoique complètement incorrecte. Kepler, sur la base d'hypothèses théologiques, croyait que l'Univers devrait être créé avec une précision mathématique, et a suggéré que les six planètes connues à ce moment se déplacent le long de sphères imbriquées inscrites et décrites autour de cinq solides platoniciens:

Dans son livre Harmonices mundi de 1619, Harmony of the World, Kepler a soutenu que de nombreuses caractéristiques de la musique, des planètes et des âmes fonctionnent selon des relations et des principes géométriques similaires. Pour confirmer les arguments, Kepler a étudié les polygones et les polyèdres, en s'intéressant particulièrement aux objets qui composent des ensembles complets, comme les solides platoniciens.

Il a étudié les «polyèdres de contact» avec lesquels paver l'avion - et a trouvé, par exemple, des « tuiles monstrueuses », comme il les appelait (consistant en pentagones, pentagrammes et décagones). Il a étudié les «polyèdres étoilés» et a trouvé diverses versions étoilées de solides platoniciens (et Kepler - Poinsot body ). En 1611, il publie un petit livre sur la structure hexagonale des flocons de neige, écrit comme cadeau pour la nouvelle année à l'un de ses mécènes. Dans ce livre, il a discuté de l'emballage tridimensionnel des sphères (et des atomes sphériques), proposant l' hypothèse que l'emballage le plus dense des boules dans l'espace tridimensionnel (nous observons régulièrement sa mise en œuvre dans les emballages de fruits dans les magasins) est un emballage cubique à face centrée (cette hypothèse n'a été formellement prouvée qu'après 2000 ans - en utilisant Mathematica).

Dans divers packages Kepler, différents polyèdres sont masqués. Partons de n'importe quelle sphère, prenons ses voisins et connectons leurs centres pour faire les sommets du polyèdre. Dans l'emballage le plus serré de Kepler, 12 autres touchent n'importe quelle sphère, et de leur centre un cuboctaèdre avec 12 sommets et 14 faces est obtenu. Mais Kepler a également décrit un autre paquet, 8% moins dense, dans lequel chaque sphère est couverte par 8 autres, et 6 autres sont très proches. Si nous connectons leurs centres, nous obtenons un dodécaèdre rhombique, avec 14 sommets et 12 faces:

Ayant découvert cela, Kepler a commencé à chercher d'autres «polyèdres rhombiques». Dans le dodécaèdre rhombique qu'il a trouvé, les losanges étaient constitués de paires de triangles équilatéraux. Mais en 1619, Kepler a également étudié les losanges dorés - et a trouvé un rhombique à trente faces, après quoi il a peint dans son livre sa belle image, à côté du dodécaèdre rhombique:

Kepler a immédiatement trouvé une application pour les polygones rhombiques: il a voulu les utiliser et un cube pour construire un modèle de sphères imbriquées adaptées aux orbites des quatre lunes de Jupiter découvertes par Galileo en 1610.

Pourquoi Kepler n'a-t-il pas ouvert l'hexaèdre rhombique? Je pense qu'il est venu assez près de lui. Il a étudié les polyèdres étoilés non convexes. Il a regardé les polyèdres rhombiques. Mais, apparemment, pour ses théories astronomiques, un rhombique à trente faces suffisait, après quoi il arrêta de chercher.

En conséquence, bien sûr, les lois de Kepler, sans rapport avec le polyèdre, sont devenues la principale contribution à l'astronomie qui lui a survécu. Mais les travaux de Kepler sur le polyèdre - quoique menés dans le cadre d’une théorie physique incorrecte - restent une contribution éternelle aux mathématiques.

Au cours des trois siècles suivants, plus de polyèdres de correction correcte ont été trouvés - et au début du XX, les mathématiciens connaissaient déjà plusieurs de leurs types:

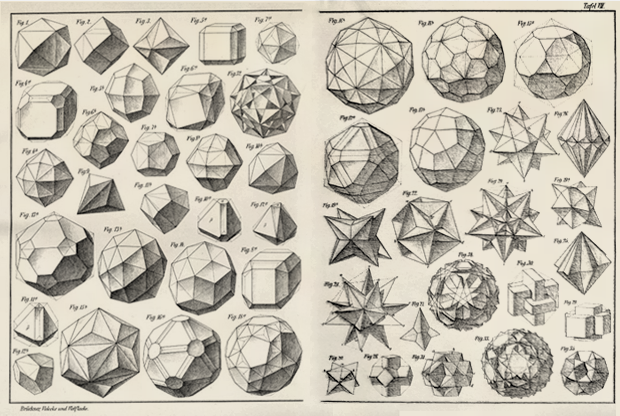
Mais, pour autant que je sache, il n'y avait pas de RS parmi eux. Sa découverte attendait le travail de Helmut Unkelbach . Né en 1910, il a soutenu son doctorat en mathématiques à l'Université de Munich en 1937 (bien qu'il ait d'abord étudié la physique). Il a écrit plusieurs ouvrages sur la cartographie conforme et - peut-être en raison de l'étude de la cartographie des polyèdres - en 1940, a publié en allemand l'ouvrage "Edge-Symmetric Polyhedra".

Il a expliqué que son objectif était une étude approfondie de tous les polyèdres possibles qui satisfont une nouvelle définition spéciale de l'exactitude: tous les bords ont la même longueur et sont dans le plan de symétrie du polyèdre. Le résultat principal du travail a été une table avec 20 polyèdres différents de cette propriété:

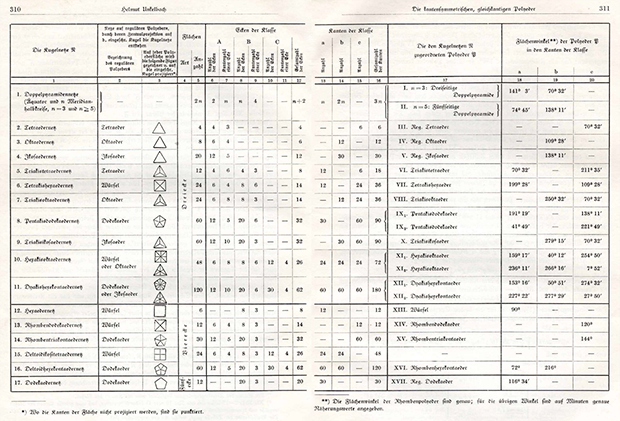Cliquable

La plupart d'entre eux étaient déjà célèbres. Mais Unkelbach en a distingué trois, qu'il considérait comme nouveaux: deux hexaciscosahèdres (ou disdakis dodécaèdre), deux hexacisicosahèdres (ou disdacystriacontahedron) et ce qu'il a appelé Rhombenhexekontaeder, ou un hexaèdre rhombique. Et il a clairement considéré RSh comme sa principale réalisation, et a inclus une photographie de son modèle faite par lui-même:

Comment a-t-il amené RS? Il a commencé avec le dodécaèdre, et a défini deux de ses plans de symétrie:

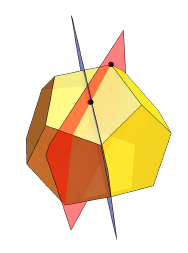
Puis divisé chacun de ses visages:

Puis, en substance, il a évincé les centres de chacune des faces d'une distance égale à la distance habituelle au centre multipliée par un certain α:

Pour α <1, les faces résultantes ne se sont pas intersectées. Mais pour la plupart des valeurs de α, leurs côtés n'étaient pas égaux. Cela ne se produit que dans un certain cas - lorsque le polyèdre résultant coïncide exactement avec le RS.

Unkelbach considérait son travail de 1940 comme un «échauffement» pour une étude plus approfondie des «polyèdres symétriques k» avec des exigences de symétrie moins strictes. Mais déjà, bien sûr, c'était un miracle qu'après le début de la Seconde Guerre mondiale , un journal mathématique ait été publié en Allemagne - peu après cette publication, Unkelbach a été appelé au front, où il a développé des torpilles acoustiques pour la flotte allemande pendant plusieurs années.

Il n'a pas publié plus d'ouvrages sur les polyèdres et est décédé en 1968. Après des années, il est revenu à la cartographie conforme et a également commencé à publier sur la théorie du vote , la considérant comme la clé pour créer une démocratie qui fonctionne bien et pensant que les mathématiciens étaient obligés de a commencé à l'utiliser.

Mais, apparaissant même dans une œuvre de 1940, la RS pourrait y rester éternellement si en 1946, Harold Scott MacDonald Coxeter ne rédigeait pas une courte critique de cette œuvre pour la revue relativement récente American Mathematical Reviews. Son examen répertorie les polyèdres mentionnés dans l'ouvrage, car un naturaliste peut répertorier de nouvelles espèces découvertes par lui lors d'une expédition. L'essentiel est qu'il y décrive "l'hexaèdre rhombique remarquable", et mentionne que "la forme de ses faces coïncide avec la forme des faces des trente faces, dont il est obtenu en donnant une forme d'étoile".

Les polyèdres n'étaient pas un sujet populaire en mathématiques au milieu du 20e siècle, mais Coxeter était leur principal partisan - et était en quelque sorte lié à tous ceux qui les étudiaient. En 1948, il a publié le livre The Right Political Scientists. Il décrit systématiquement différentes familles de polyèdres réguliers, en particulier, et le grand polyèdre étoilé à trente faces - en fait, contenant un RS:

Mais dans son livre, Coxeter ne mentionne pas explicitement RS, et bien qu'il ait été honoré des références de certains amateurs de polyèdres, RS a continué à être peu connu.

Quasi-cristaux

Les cristaux ont toujours été des exemples importants de polyèdres dans la nature. Mais au 19ème siècle, alors que la théorie atomique gagnait de plus en plus de reconnaissance, les scientifiques ont commencé à mener des recherches de plus en plus sérieuses dans le domaine de la cristallographie et de l'arrangement des atomes dans les cristaux. Les polyèdres ont commencé à apparaître fréquemment, en particulier dans les représentations de la géométrie des blocs répétitifs d'atomes («cellules») dans les cristaux.

En 1850, on savait qu'il ne pouvait y avoir que 14 géométries de ce type - parmi elles, il y en a également une basée sur le dodécaèdre rhombique. Ils se distinguent par la présence de symétries de deuxième, troisième, quatrième ou sixième ordre - ce qui, en substance, est une conséquence du fait que l'espace ne peut être rempli qu'avec certains polyèdres, tout comme seuls les polygones réguliers tels que les carrés peuvent remplir un plan bidimensionnel, triangles et hexagones.

Qu'en est-il des autres matériaux non cristallins - comme les liquides ou le verre? Depuis le début du XXe siècle, on s'intéresse à la possibilité de la présence d'au moins des symétries du cinquième ordre approximatives. Il ne sera pas possible de remplir l'espace avec les icosaèdres corrects, mais il peut être possible de créer des sections d'espace à vingt côtés avec de petits espaces entre eux.

Cette question n'a pas été résolue jusqu'aux années 1980, lorsque la cristallographie par diffraction d'électrons utilisant un alliage d'aluminium et de manganèse refroidi rapidement a démontré la présence d'une symétrie quintuple. Des théories pour atteindre cette symétrie existaient déjà, et après quelques années, des images faites au microscope électronique sont également apparues, sur lesquelles des particules ayant la forme d'un losange à trente faces étaient visibles:

Et tandis que les gens imaginaient comment ces trente-heptaèdres peuvent être combinés les uns avec les autres, un hexaèdre rhombique est apparu comme un «trou» dans un groupe de 12 trièdres rhombiques:

Au début, on l'appelait une étoile à 20 branches. Mais ensuite, il a été associé à des descriptions dans la littérature sur le polyèdre et identifié comme RS.

Pendant ce temps, l'idée de créer des objets à partir d'éléments rhombiques gagnait en popularité. Michael Longe Higgins, océanographe et spécialiste de la formation des vagues océaniques, a rejoint le hobby de masse et, en 1987, il a breveté un jouet basé sur des éléments rhomboédriques, à partir duquel il était possible d'assembler une «étoile Kepler» (RS) ou une «boule Kepler» (rhombique trente ):

Et - même si je ne l'ai découvert que maintenant - les blocs rhomboédriques, que nous avons envisagés en 2009 comme une option pour créer des «Shipastiks», ont en fait été produits par la société Dextro Mathematical Toys (Rhombo.com), qui travaillait à la base de Longge-Higgins à San Diego

La question de réussir à remplir l'espace avec des figures en trois dimensions - ou même un avion avec des figures en deux dimensions - est plutôt compliquée. On sait depuis les années 1960 que dans le cas général, le problème de savoir si un certain ensemble de formulaires peut remplir un avion est insoluble. (En principe, on peut vérifier si 1000 de ces formulaires peuvent être composés les uns avec les autres, mais plus nous considérons de formulaires, plus cela nécessitera de ressources informatiques).

Des gens comme Kepler ont probablement supposé que si un ensemble de formes pouvait remplir un plan, cela pourrait être fait comme un motif répétitif. Cependant, après qu'il est devenu clair que, dans le cas général, ce problème n'était pas résolu, Roger Penrose a proposé en 1974 deux formes qui peuvent remplir l'avion sans répéter les motifs. En 1976, Penrose (et Robert Ammann) avaient mis au point une version simplifiée de ces formulaires:

Et, oui, ces formes ressemblent à des losanges, mais pas à de l'or. Mais avec des angles de 36 °, 144 ° et 72 °, 108 °, ils ont une symétrie 5 fois et 10 fois.

Ces losanges ne peuvent pas disposer de motifs répétitifs. Mais il s'avère qu'ils peuvent tracer un motif construit de manière imbriquée systématique:

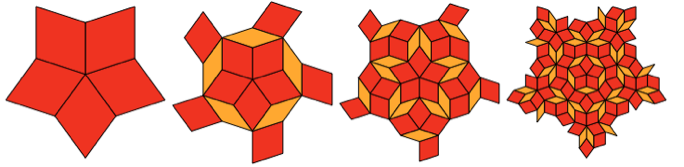
Et, oui, la partie médiane de la 3e étape est très similaire au Shipastik aplati. Mais cela ne coïncide pas complètement avec lui, les losanges externes ont un format légèrement différent.

Cependant, un lien étroit entre eux existe toujours. Imaginez que nous partions non pas d'un avion, mais d'une moitié d'un losange tridimensionnel de trente carrés, composé de losanges dorés:

D'en haut, il ressemble exactement au début de la conception de la mosaïque Penrose imbriquée. Si nous continuons ce processus, nous obtenons cette mosaïque:

Si vous le regardez «de côté», vous pouvez voir que ce sont toujours les mêmes losanges dorés:

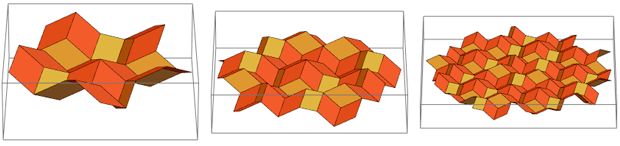
Après avoir compilé quatre de ces «toits Wieringa», vous pouvez obtenir juste RS:

Quelle est la relation entre ces structures intégrées et la véritable façon de former des quasi-cristaux physiques? Ce n'est pas encore clair. Mais il est assez intéressant de voir comment les notes de RS apparaissent dans la nature.

Historiquement, c'est grâce à la discussion sur les quasi-cristaux que Sandor Kabaei a commencé à étudier la RS en utilisant Mathematica, ce qui a conduit Eric Weinstein à les découvrir, ce qui a conduit à leur inclusion dans Mathematica et Wolfram Language, ce qui m'a amené à choisir l'un d'entre eux pour notre logo. En l'honneur de cela, nous imprimons une mosaïque Penrose à l'intérieur de notre Paper Shipastik:

Aplatissement de l'épine

Notre Shipastik pour Wolfram | Alpha a éclaté dans le monde en 2009 avec la sortie de Wolfram | Alpha. Mais nous avons également notre Shipastik pour Mathematica, qui se développe et évolue depuis longtemps. Par conséquent, lorsque nous avons construit notre nouveau siège européen en 2011, deux Shipastik se disputaient la présence.

Notre directeur artistique de longue date, Jeremy Davis, a proposé ce qui suit: prendre l'un des Shipastiks et «l'idéaliser» en utilisant uniquement son «squelette». La décision de commencer avec RS était simple. Mais ensuite nous l'avons aplati, et donc la première version du logo maintenant familier est apparue:

Surprise brésilienne

Quand j'ai commencé cet article, je pensais que toute l'histoire s'arrêterait là. Après tout, j'ai déjà décrit comment nous avons choisi RS pour nous-mêmes et comment les mathématiciens l'ont inventé. Mais avant de finir d'écrire, j'ai décidé: "Je vais parcourir toutes les lettres sur Shipastik pendant toutes les années, juste pour m'assurer que je n'ai rien raté."

Et puis j'ai remarqué un e-mail de juin 2009 de l'artiste brésilienne Yolanda Kipriano. Elle a écrit qu'elle avait vu un article sur Wolfram | Alpha dans un magazine d'information brésilien, attiré l'attention sur Shipastika et fourni un lien vers son site. Plus de 9 ans se sont écoulés depuis, mais j'ai toujours suivi ce lien et j'ai été étonné de voir ce qui suit:

J'ai continué à lire sa lettre: "Au Brésil, cet objet s'appelle Giramundos ou la" fleur de Mandakaru "et est fait de serviettes comme ornement artistique."

Quoi?! Au Brésil, il existe une tradition associée à Shipastik, et pendant toutes les années, nous n'en avons pas entendu parler? Bientôt j'ai découvert ses images sur le net. Une petite partie des modèles était en papier, la plupart en tissu - mais il y en avait beaucoup:

J'ai écrit à mon ami brésilien qui a travaillé sur les premières versions de Wolfram | Alpha. Il a rapidement répondu: «Ces objets semblent vraiment familiers. À ma honte, je n’avais pas assez envie de comparer deux et deux », et m’a envoyé des photos du catalogue local d’œuvres d'art et d'artisanat:

La chasse a commencé: quels étaient ces objets et d'où venaient-ils? Quelqu'un de notre entreprise a dit que son arrière-grand-mère du Chili a crocheté de telles choses et en a toujours fait une queue. Nous avons commencé à entrer en contact avec des gens qui ont publié des photos de «shipastiks folk» sur le net. Il s'est avéré assez souvent qu'ils achetaient leurs exemplaires dans les magasins. Mais parfois, les gens disaient qu'ils savaient comment les fabriquer. Et tout le monde avait presque la même histoire: ils ont appris cela de leurs grands-mères.

Une façon typique de collecter des pointes folkloriques - au moins à notre époque - est de couper 60 diamants en carton. Ensuite, tout le monde doit être enveloppé dans du tissu et les coudre ensemble:

Mais alors un problème mathématique se pose immédiatement. Ces personnes marquent-elles et sculptent-elles correctement les losanges dorés avec un angle de 63 °? Habituellement non. Ils font des losanges à 60 ° à partir de paires de triangles équilatéraux - c'est la forme rhomboïde standard utilisée dans la fabrication de courtepointes. Alors, comment les Thornies se produisent-ils? Eh bien, la différence entre 60 ° et 63 ° est petite, et si vous cousez les faces ensemble, il y aura suffisamment d'espace entre elles pour la manœuvre, il est donc assez simple de faire un polyèdre sans obtenir des angles absolument précis. (Il y a aussi des quasi-Shipastiks, dans lesquels, comme dans la construction d'Unkelbach, au lieu de faces il n'y a pas de losanges, mais des «triangles externes» tranchants).

Les pics sur Internet sont désignés différemment. Le plus souvent - Giramundos. Ils sont souvent appelés Estrelas da Felicidade ("étoiles du bonheur"). Le fait qu'elles soient parfois appelées «étoiles moraves» prête à confusion, mais en fait, les étoiles moraves sont des polyèdres beaucoup plus nets (le plus souvent en rhombocubooctaèdre), qui ont récemment gagné en popularité en tant que luminaires.

Malgré une longue enquête, je ne connais toujours pas toute l'histoire des pointes folkloriques. Voici ce que j'ai découvert. -, ( ). -, , XX , , , . , , , .

, , , ---. , , , - « 50».

( «») , , , , . – , – , ( - ), , 15 .

? . , , , 1900 . , 80- , , 200- , , , .

, , , . , . , – - , , .

: , . , . – , , .

? 1750 , . XX – , 13 – . , – , – .

, , . - XX – , , , – . 1950- .

. ( ) , « . » ( – ) - (.. «»), .

, . - — Flor Mandacarú ( ). – Carambola ( , « »). – Pindaíva ( ).