Civilisation printanière, 1/5

### Partie 1. Golden "Ku"

Vers six ans, je suis tombé entre les mains d'un guide de grand-père ^[50] sur des camions du milieu du XXe siècle. Solide, imprimé sur papier épais et lisse, livre rare. La seule chose qui reste dans la mémoire de mon grand-père après l'effondrement du pays, les guerres et les voyages.



Le livre de référence contenait de nombreuses caractéristiques de performance intéressantes, donc le mot «capacité de charge» m'est devenu familier dès la petite enfance. Et quand mon père en promenade a mentionné qu'un camion pèse autant qu'il le faut, je m'en souviens. Il s'en souvenait et, beaucoup plus tard, il s'est intéressé.

Père avait raison. Pour les camions des années 60, cette règle est mise en œuvre avec une précision assez surprenante:



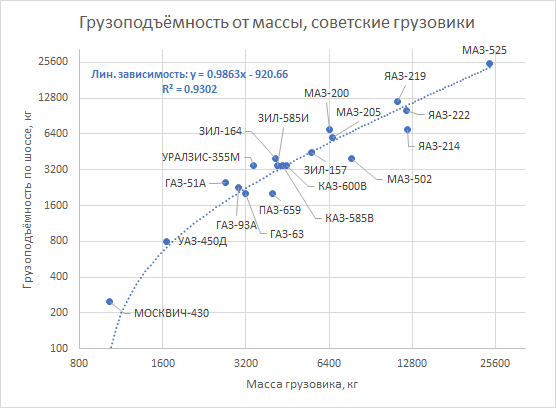
Il est beaucoup plus curieux que ce schéma soit également observé pour les véhicules totalement différents des camions.

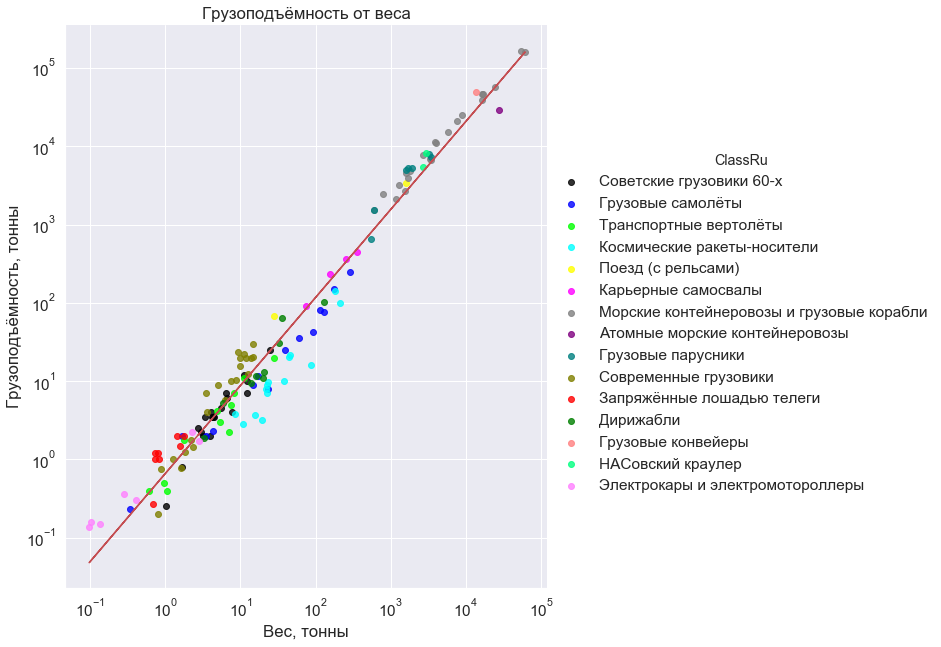
Au début, pour le plaisir, j'ai mis des avions cargo à l'horaire. Et a été surpris. J'ai commencé à ajouter d'autres véhicules. Equitation, flottant et volant, construit au cours des siècles des 19e, 20e et 21e, travaillant sur l'énergie du thermique, de l'atomique, du vent et même du cheval. Résultat? Faible puissance (indicateur 1.125), sinon simplement linéaire, la dépendance. Sur des masses de centaines de kilogrammes à soixante mille tonnes. Avec des écarts, bien sûr, où pourrait-on s'en passer, jusqu'à 10 fois parfois, mais sur six ordres de masse, c'est évidemment une bagatelle.

La voici, cette dépendance, serrant à la diagonale d'un vaste champ vide:


Sur le graphique noté: avion cargo; hélicoptères de transport; dirigeables, modernes et du début du siècle; lanceurs spatiaux (en orbite basse); Camions soviétiques des années 60; camions miniers modernes; des camions modernes de Russie, des États-Unis, de Chine et d'Inde; voitures et scooters électriques; trains (avec rails); porte-conteneurs nucléaires; porte-conteneurs et cargos (pas de pétroliers); voiliers de 17 à 20 siècles; bandes transporteuses pour le transfert de minerai; Tracteur Nassovsky pour l'exportation de missiles au départ; et enfin des charrettes tirées par des chevaux.

Si vous entrez la valeur de Q , définie comme la masse de la cargaison transportée par rapport à la masse sèche du véhicule, voici à quoi elle ressemble pour chacun des groupes:



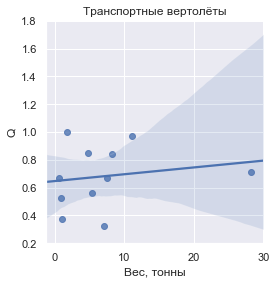
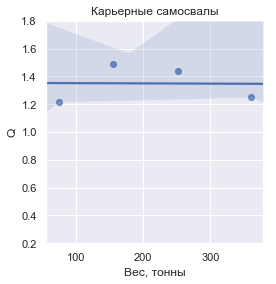
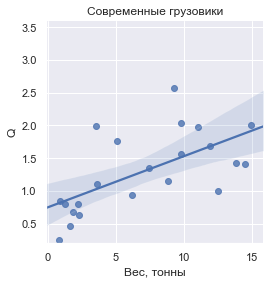
En chiffres, les valeurs Q sont:

Classe d'actifs	Q moyen	Écart type Q
Avion cargo	0,667091	± 0,206162
Hélicoptères de transport	0,681605	± 0,225062
Dirigeables, modernes et du début du siècle	0,842673	± 0,374622
Lanceurs spatiaux (orbite basse)	0,372446	± 0,1555810
Camions soviétiques des années 60	0,7777435	± 0,232425
Camions miniers modernes	1,349610	± 0,136840
Camions modernes de Russie, USA, Inde, Chine	1.293679	± 0,604313
Cartes et scooters électriques	1.098433	± 0,343791
Train (avec rails)	2.275989	± 0,205999
Navire porte-conteneurs nucléaire	1.035233	± NA
Navires porte-conteneurs et cargos (non pétroliers)	2.556004	± 0,378040
Navires à voile des 17-20 siècles	2.488461	± 0,671785
Courroies transporteuses de fret	3.703704	± NA
Tracteur Nasovsky pour le lancement de missiles	2,355919	± 0,525174
Chariots tirés par des chevaux	1,203061	± 0,389183

Comme on peut le voir, Q, bien que pas partout, soit strictement singulier, mais au sein de chaque groupe tend vers une valeur commune proche de l'unité.


Cela me semblait ... mystérieux. Pourquoi un voilier en bois, une voiture électrique en aluminium et un porte-conteneurs atomique qui contient cent mille voitures électriques augmentent-ils plus ou moins leur poids? Qu'est-ce qui nous fait créer des véhicules de qualité Q ≈ 1 sur des masses différentes de milliers de fois? S'agit-il d'une manifestation des propriétés de la physique mondiale, de l'économie terrestre, est-ce une limitation de l'intelligence humaine? Dans quelle mesure cette loi est-elle universelle, sera-t-elle appliquée aux civilisations d'autres étoiles? Problèmes mondiaux. Il est peu probable qu'ils soient résolus ici et maintenant. Mais ici, il est possible et nécessaire de considérer et de mordre combien cela se révélera. Voilà ce que nous allons faire.

Le record du monde ^{[ 180 ] de} levage d'un haltère par une personne de poids moyen dépasse 200 kg. Théoriquement, cela signifie que notre corps a une marge de sécurité pour les charges saccadées au moins jusqu'à Q = 2,5. Cependant, cela nécessite des forces et une formation si exorbitantes qu'elles ne sont jamais utilisées dans les activités quotidiennes. Il est plus conseillé d' emballer le sucre dans des sacs de 50 kilos, bien que cela nécessite quatre fois plus de chargeurs ou une marchette. A noter que cette situation est le résultat d'une évolution biologique, à laquelle l'intellect humain n'a pas (presque) participé, et a donc un «alibi» en lui.

La physique et l'ingénierie à elles seules n'interdisent pas les Q élevés. Il y a une turbopompe à hydrogène pour le moteur en vol Shuttle, cette petite chose à droite sur l'image qui développe 54 mégawatts de puissance ^{[ 60 ]} avec un poids total du véhicule de 350 kg:

[Crédit d'image: [ 10 ]]

Si, en simplifiant, évaluez Q par la puissance par kilogramme de masse, alors c'est 100 fois plus élevé que celui d'une voiture décente. Mais cette chose est presque comme une fusée! Il est moins cher de fabriquer 100 voitures avec Q = 1 et de transporter la cargaison avec elles, plutôt que d’essayer de «atteler» cette unité à un chariot à roues.

De telles considérations suggèrent que les raisons ici sont économiques. De plus, non pas dans le sens étroit d'économies et de pays spécifiques (parce que nos appareils sont générés par des peuples et des systèmes très différents), mais plutôt dans le sens de «l'opportunité des efforts». La pertinence est suffisamment universelle pour, apparemment, s'appliquer à des produits très différents et quelque part même aux animaux.

_{L'article a été écrit pour le site https://habr.com . Lors de la copie, veuillez vous référer à la source. L'auteur de l'article est Evgeny Bobukh .}

Essayons d'étudier quantitativement les limites de cette opportunité. Nous posons la question: comment le coût d'un appareil à masse fixe dépend-il de Q ? Ici, par exemple, il y a un camion à benne pesant 10 tonnes, il faut 10 tonnes de fret. On veut aussi faire un 10 tonnes, mais en emportant 20 tonnes ( Q = 2) voire 50 ( Q = 5). Au même niveau de développement technologique, le même volume de production. Il est clair que des charges plus élevées augmenteront les exigences pour les matériaux (acier -> titane?), Et pour les moteurs (autres températures, pressions) et pour l'ingénierie (moins de tolérances aux erreurs, conceptions plus délicates). De toute évidence, à mesure que Q grandit, tout sera plus cher. Mais combien de fois, par rapport aux dix tonnes?

Cette tâche, bien sûr, n'est pas anodine. Néanmoins, certaines estimations peuvent être obtenues à partir des considérations les plus générales. Ce que nous allons faire maintenant.

Nous introduisons la fonction C ( Q ). Il décrit le coût le plus bas possible d'un appareil avec une efficacité de Q , exprimé en coûts d'un appareil similaire de même masse à Q = 1. Que sait-on à ce sujet?

1. C (1) = 1, par définition.

2. C ( Q ) est une fonction continue, au moins jusqu'à ce que la différence de masse soit mesurée par des atomes en morceaux. Intuitivement, il semble assez fluide pour avoir les premiers dérivés. Je pense que nous pouvons admettre (comme pour la plupart des fonctions physiques) qu'il est généralement analytique.

3. C ( Q ) est une fonction strictement croissante. Plus la qualité de Q est élevée, plus il est difficile de réaliser la structure et plus elle est chère. C'est-à-dire dC ( Q ) / dQ > 0 au moins pour Q > 0.

4. Avec Q supérieur à environ 3, C ( Q ) commence à augmenter plus rapidement que linéairement. Pourquoi? Parce que nous voyons qu'il est moins cher pour les gens de fabriquer trois camions pour dix tonnes avec Q = 1 que un pour trente avec Q = 3. En résumé, nous écrivons: k * C (1) < C ( k ) pour k > ≈3 - autre en mots, C ( k ) croît plus vite que k , pour k > ≈3.

5. De même, étant donné que dix avions avec Q = 0,1 sont clairement non rentables qu'un avec Q = 1 (parce qu'ils construisent le deuxième, pas le premier), pour k > ≈3, nous avons: k * C (1 / k )> C (1), ou C (1 / k )> 1 / k .

6. Le coût de la pompe de la navette laisse entendre qu'au moins jusqu'à Q ~ 100, la valeur de C ( Q ) n'augmente pas en tant qu'exposant avec un indicateur significatif. Sinon, ce TNA ne coûterait pas des millions de dollars, mais une sorte de 10 ²⁰ $, et nous aurions à peine réussi. C'est-à-dire C (100) se situe autour de 10 ³ - 10 ⁸ , mais pas du tout 10 ¹⁵ .

7. À quoi C (0) est-il égal? C'est le coût de l'appareil, qui peut toujours se déplacer lui-même, mais ne peut emporter aucune cargaison. De toute évidence, un tel "camion" est moins cher qu'un camion complet. Mais combien de fois? L'histoire le montre parfois plutôt que des dizaines ou des centaines. Une quinzaine d'années se sont écoulées entre le premier avion capable de se déplacer seul ( Q = 0) et le transport de marchandises par avion. Des premières voitures à essence aux camions assez décents avec Q = 1,5 ([ 120 ] + [ 130 ]), un peu plus. Si ce développement avait été d'une complexité incroyable, il ne se serait guère achevé aussi rapidement. Par conséquent, la difficulté de fabrication et le coût d'un véhicule avec Q = 0 ne devraient pas être complètement radicalement différents de ceux de Q = 1. Par conséquent, nous nous attendons à ce que C ( 0 ) se situe quelque part entre 0,1 et 0,5.

8. Cette fonction a-t-elle un sens pour un Q négatif? Tout à fait! Un camion avec Q = -0,5 est un camion qui ne se déplacera que si vous retirez la moitié de son poids d'une grue à tour. Et Q = -1 - c'est un chariot développant une traction nulle. Capable de transporter du fret uniquement si vous le prenez en remorque. Autrement dit, généralement sans moteur. De toute évidence, son coût, sinon non nul, est très faible. Par conséquent, mettez C (-1) ≈ 0.

9. Et qu'est-ce que C (-2)? C'est le coût d'un appareil qui doit être tiré avec au moins deux fois son poids pour se déplacer! Oui, les zones Q <-1 sont les ancres, fondations, pieux, freins. Dispositifs qui empêchent le mouvement. Là, bien sûr, il y a une dynamique complètement différente et ses propres lois, mais au moins on voit que C ( Q ) ne se termine pas par une singularité pour Q <-1, et que dans la région Q = -1 il a un minimum, et donc, au moins au moins Un petit voisinage de ce point C ( Q ) devrait se comporter comme une parabole.

Ainsi, l'esquisse C ( Q ) ressemble à ceci:


Nous développons C ( Q ) dans une série de Taylor au point Q = -1:



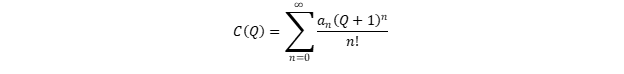
Il résulte de la propriété (8) que a ₀ = 0. Les propriétés (4), (5) et en partie (9) suggèrent que a _{1 est} proche de zéro, ou en tout cas, que sa contribution ne domine pas dans l'intervalle 0 .. .3.

Et puis il s'avère que le premier terme non nul dans l'expansion de C ( Q ) est parabolique, et qu'avec Q dans la région des unités C ( Q ) se comporte approximativement comme une fonction quadratique ou un peu plus rapide:

C ( Q ) ≈ a ₂ * ( Q +1) 2/2 + O (( Q + 1 ) ³ )

Et de [1] il s'ensuit qu'un ₂ ≈ 1/2.

Enfin, comme au moins jusqu'à Q ~ 100, la fonction C ( Q ) n'est toujours pas exponentielle (propriété (6)), nous pouvons la mettre égale à Q ^p avec l'exposant p quelque part dans la région de 2 ... 4. À peine plus.

Conclusion: Pour une masse fixe, le coût du dispositif C (Q) n'augmente pas plus faible que (Q + 1) 2/4, mais pas plus vite qu'environ O (Q ⁴ ) [1]

Est-il possible de regarder la véritable dépendance de C ( Q ) pour comprendre à quel point cette conclusion est correcte? C’est dur. La plupart des mécanismes créés par l'homme sont des masses différentes, mais fixent Q dans la région de l'unité. Nous avons besoin du contraire: approximativement la même masse, mais un Q. différent Au début, j'espérais des données sur les moteurs d'avion ... mais le travail ^{[ 70 ] [ 80 ]} sur leur tarification est très drôle. Les prix des moteurs y sont classés et seules les formules de prévision et les erreurs moyennes sont publiées.

Heureusement, l'aide est venue des voitures ^{[ 150 ]} . C'est avec eux, à peu près de même masse, que l'on trouve des moteurs de différentes capacités. Et bien que la puissance ne soit pas encore une cargaison transportable, avec un certain effort d'ingénierie, elle y est approximativement proportionnelle. Ce qui nous permet d'estimer si notre formule est proche de la réalité.

Il semble que oui:

[Source: [ 150 ]]

Les points bleus sont de vraies voitures. En première approximation, leur prix augmente en densité de puissance au degré de 2,3.

Points rouges - le prix calculé par la formule [1], sur la base de l'hypothèse que Q = 1 correspond aux voitures les moins chères par kilogramme de l'ordre de 20 à 30 000 $. On peut voir que la formule donne vraiment une bonne estimation de C ( Q ) par le bas (là où nous visions).

Quand on regarde la masse de ces points savoureux, il y a une forte tentation: dessiner C ( Q ) à travers eux et donc étudier directement la dépendance. Cela ne peut pas être fait. Principalement parce que le prix d'une voiture de tourisme n'est pas seulement déterminé par ses caractéristiques de traction. Il est difficile d'imaginer une voiture de cent kilobaxes dans laquelle il n'y a pas la meilleure climatisation, les sièges les plus confortables et le "cendrier en platine avec lunette rhodiée". Et tout cela coûte de l'argent qui n'a rien à voir avec notre C ( Q ). Cependant, ici la «branche» inférieure des voitures, passant presque exactement selon le C ( Q ) calculé, semble intéressante. J'ose admettre que ce ne sont que des voitures sans fioritures. Où "pas de dames, mais d'aller." Mais plus de 100 000 $ pour une voiture, ceux-ci ne sont plus là.

_{L'article a été écrit pour le site https://habr.com . Lors de la copie, veuillez vous référer à la source. L'auteur de l'article est Evgeny Bobukh .}

Ainsi, nous sommes en mesure d'estimer le coût des appareils à Q élevé, au moins par ordre de grandeur. Pourquoi était-ce nécessaire?

Mais pourquoi. Jetez un œil à la première étape du transporteur spatial. Eh bien, au moins Proton-M ^{[ 110 ]} , pour le concret. C'est un véhicule à part entière, avec des moteurs, un système de contrôle, une marge de sécurité décente et un poids à sec de 31 tonnes. En même temps, au début de la fusée, il traîne sur sa bosse non seulement la charge utile, mais aussi tout le carburant, tous les étages supérieurs et, bien sûr, lui-même. Au total - 683 tonnes. Plus surcharge de démarrage, total (effectif) 1068 tonnes de charge! Du point de vue de la première étape, cela fonctionne dans un mode terrible Q = (1068/31) = 34,4! C'est l'équivalent de 50 tonnes de marchandises empilées sur une voiture de tourisme.

Et nous savons que le coût d'un appareil avec un Q élevé est au moins (Q + 1) 2/4 fois plus élevé que quelque chose de similaire avec Q ≈ 1. Pour Proton, cela équivaut à ... 313 fois.

Autrement dit, le Proton devrait coûter 300 fois plus cher qu'un appareil similaire avec Q = 1. Et ce chiffre dépend peu du progrès et de la technologie. Car dès que les "scientifiques britanniques" inventent un superalliage qui rend une fusée moins chère, alors les moteurs au sol deviennent aussi moins chers. Par conséquent, une fusée chimique, même réutilisable, sera toujours très chère. Qu'on le veuille ou non.

Bon. Disons 300 fois. Mais par rapport à quoi ? Serait-il intéressant de comparer nos calculs avec certains appareils objectivement existants pour éliminer les erreurs grossières?

Malheureusement, il n'y a pas de missiles de trente tonnes avec Q = 1. Mais il existe des analogues approximatifs pouvant être comparés:

• Le tout premier est un camion minier. Oui, pas une fusée. Mais encore, c'est aussi un moteur thermique, une ingénierie pas tout à fait banale, et l'un des moyens les moins chers pour transporter des marchandises. Et si l'on parle déjà d'exploration spatiale, le camion ne devrait-il pas être le prototype du modèle économique de la cabine spatiale? Essayons donc, au moins pour une estimation générale. Voici un Belaz-7540 de 30 tonnes. Le prix du marché ^{[ 140 ]} est de 3,7 millions de roubles, soit 62 000 $. Pour Proton, cela est converti au coût de la première étape dans la région de 19 millions de dollars. Wikipedia représente ^{[ 100 ]} un coût de démarrage de 65 millions de dollars. Assez proche, étant donné que ce montant comprend beaucoup plus, à l'exception du prix de la toute première étape.
• Dans [ 160 ], une plate-forme expérimentale de fusée sur rails est décrite. Une masse de 10 tonnes, en cinq étapes, accélère à 4 km / s. Le prix est de 750 kilobax. À en juger par les images et les paramètres publiés, cet appareil fonctionne quelque part avec Q = 10. Pas une unité, mais toujours pas 34. Si vous partez de ces chiffres, la première étape du Proton devrait coûter quelque 23 millions de dollars.
• En général, quand j'essaie d'imaginer une fusée avec Q = 1, dans mon esprit, il y a une sorte de gros blanc avec une petite encoche remplie de poudre à canon. La poudre à canon brûle et pousse le blanc vers l'avant. Un peu, vous n'accélérerez pas autant. J'ai tergiversé cette photo pendant deux jours, jusqu'à ce que je réalise qu'elle me rappelle. C'est ... un marteau pneumatique! Où le gaz se dilate et pousse le blanc. L'ultime bastardisation de l'idée d'un turboréacteur, préservant toujours une sorte de parenté. Eh bien, nous cherchons. Oui, voici le ^{[ 170 ]} marteau pneumatique Stanko M212. Le poids du disque est de 2 tonnes, la structure entière est de 58,3 tonnes. Le système Q est donc un modeste 0,034. Vendu pour 40 mille euros. Si nous extrapolons le coût de cette blague à Q = 34,4 selon la formule [1], nous obtenons ... 47 millions d'euros. Soit 24 millions en proportion de plus de 30 tonnes.

Il semble que nous ne soyons pas vraiment séparés de la réalité.

Pour résumer. Étant donné que les fusées, même réutilisables, coûtent 2 à 3 ordres de grandeur plus chers que les camions, tout peuplement spatial fait de matériaux au sol coûtera également 100 à 1 000 fois plus cher que ses homologues au sol. Il s'agit d'un obstacle très important au développement.

Les missiles sont chers car ils sont très lourds et sont obligés de travailler lorsqu'ils sont malsains à un Q. élevé. Mais pourquoi les roquettes sont-elles lourdes? La réponse (qui est un peu plus profonde que la formule de Tsiolkovsky) sera examinée dans la deuxième partie.

À suivre .

Mise à jour: plusieurs personnes ont tenté de souligner les ambiguïtés concernant le carburant lors de l'examen des missiles. J'y ai pensé. Et j'ai réalisé qu'il y a vraiment une inexactitude dans l'article. Vu dans les commentaires ici .