Filtre de Kalman pour minimiser la valeur d'entropie d'une erreur aléatoire avec une distribution non gaussienne

Présentation

Chez Habr, une description mathématique du fonctionnement du filtre de Kalman et des caractéristiques de son application a été examinée dans les publications suivantes [1 ÷ 10]. Dans la publication [2], l'algorithme du filtre de Kalman (FC) dans le modèle «espace d'état» est considéré sous une forme simple et intelligible. Il convient de noter que l'étude des systèmes de contrôle et de gestion dans le domaine temporel à l'aide de variables d'état a été largement utilisée récemment en raison de la facilité d'analyse [11].

La publication [8] présente un intérêt significatif spécifiquement pour la formation. La technique méthodique de l'auteur est très efficace. Il a commencé son article en considérant la distribution de l'erreur gaussienne aléatoire, a considéré l'algorithme FC, et a fini avec une formule itérative simple pour sélectionner le gain FC. L'auteur s'est limité à un examen de la distribution gaussienne, citant le fait que pour suffisamment $$$n$ (mesures multiples) la loi de distribution de la somme des variables aléatoires tend vers la distribution gaussienne.

Théoriquement, une telle affirmation est certainement vraie, mais en pratique, le nombre de mesures à chaque point de la plage ne peut pas être très élevé. Kalman RE lui-même a obtenu des résultats sur la covariance minimale du filtre sur la base de projections orthogonales, sans supposer que les erreurs de mesure sont gaussiennes [12].

Le but de cette publication est d'étudier les capacités du filtre de Kalman à minimiser la valeur d'entropie d'une erreur aléatoire avec une distribution non gaussienne.
Pour évaluer l'efficacité du filtre de Kalman à identifier la loi de distribution ou une superposition de lois à partir de données expérimentales, nous utilisons la théorie de l'information des mesures basée sur la théorie de l'information de C.Shannon, selon laquelle l'information, comme une quantité physique, peut être mesurée et évaluée.

Le principal avantage de l'approche informationnelle pour la description des mesures est que la taille de l'intervalle d'entropie d'incertitude peut être trouvée strictement mathématiquement pour toute loi de distribution. Cela élimine l'arbitraire historiquement développé qui est inévitable avec l'attribution volontaire de diverses valeurs de probabilité de confiance. Ceci est particulièrement important dans le processus éducatif, lorsque l'élève peut observer une diminution de l'incertitude de mesure lors de l'application du filtrage de Kalman sur un échantillon numérique donné [13,14].

De plus, la combinaison des caractéristiques probabilistes et informationnelles de l'échantillon peut déterminer plus précisément la nature de la distribution des erreurs aléatoires. Cela s'explique par une vaste base de données de valeurs numériques de paramètres tels que le coefficient d'entropie et le contre-excès pour diverses lois de distribution et leur superposition.

Évaluation de la superposition des lois de distribution d'une variable aléatoire par le coefficient d'entropie et le contre-excès (obtenu à partir de données expérimentales)

Densité de distribution de probabilité pour chaque colonne de l'histogramme [14] large $$$d$ est égal à $$$p_ {i} (x_ {i}) = n_ {i} / (n \ cdot d)$ , d'où l'estimation des probabilités d'entropie est définie comme $$$H \ left (x \ right) = \ int _ {- \ infty} ^ {+ \ infty} p \ left (x \ right) \ ln p \ left (x \ right) dx$ lors de la recherche de l'entropie par l'histogramme de $$$m$ colonnes, nous obtenons le rapport:

$$$\ displaystyle H \ left (x \ right) = - \ sum_ {i = 1} ^ {m} \ int _ {\ tilde {x_ {i}} - \ frac {d} {2}} ^ {\ tilde { x_ {i}} + \ frac {d} {2}} \ frac {n_ {i}} {nd} \ ln \ frac {n_ {i}} {nd} = \ sum_ {i = 1} ^ {m } \ frac {n_ {i}} {n} \ ln \ frac {n} {n_ {i}} + \ ln d$

Nous présentons l'expression d'estimation de l'entropie sous la forme:

$$$H \ left (x \ right) = \ ln \ left [d \ prod_ {i = 1} ^ {m} \ left (\ frac {n} {n_ {i}} \ right) ^ {\ frac {n_ {i}} {n}} \ droite]$

Nous obtenons une expression pour estimer la valeur d'entropie d'une variable aléatoire:

$$$\ Delta _ {e} = \ frac {1} {2} e ^ {H \ left (x \ right)} = \ frac {dn} {2} 10 ^ {- \ frac {1} {n} \ sum_ {1} ^ {m} n_ {i} \ lg n_ {i}}$

La classification des lois de distribution est effectuée sur un plan dans les coordonnées du coefficient d'entropie $$$k = \ frac {\ Delta _ {e}} {\ sigma}$ et contre-excès $$$\ psi = \ frac {\ sigma ^ {2}} {\ sqrt {\ mu _ {4}}}$ où $$$\ mu _ {4} = \ frac {1} {n} \ sum_ {1} ^ {n} \ left (x_ {i} - \ bar {X} \ right) ^ {4}$ .

Pour toutes les lois de distribution possibles, \ psi varie de 0 à 1 et k de 0 à 2,066, de sorte que chaque loi peut être caractérisée par un certain point. Nous le montrons en utilisant le programme suivant:




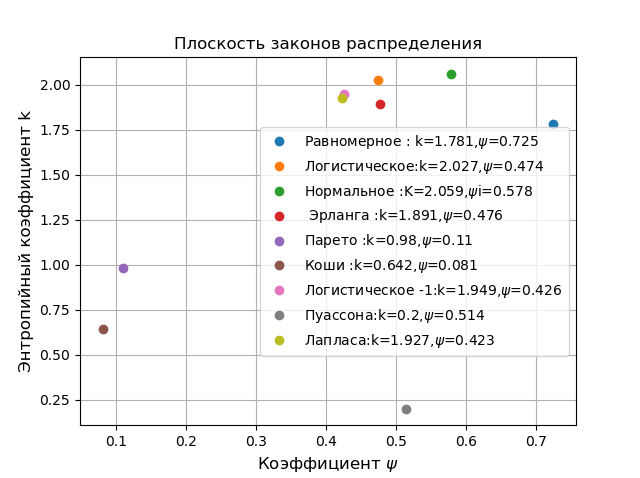
Dans un avion en coordonnées $$$k, \ psi$ retirées du reste des distributions, les distributions de Pareto, Cauchy, bien qu'elles appartiennent à différents domaines d'application, le premier en physique et le second en économie. Pour comparaison, choisissez la distribution gaussienne normale en haut de la classification. Toutes les comparaisons ci-dessous sont effectuées sur un échantillon limité et sont de nature à démontrer les capacités d'un cristal photonique à l'aide de l'exemple d'une détermination numérique de l'erreur d'entropie.

Choix d'un algorithme de filtre de Kalman

À chaque point sélectionné dans la plage de mesure, plusieurs mesures sont effectuées et leur résultat est comparé à une mesure que FC «ne sait pas». Par conséquent, vous devez choisir un FC, par exemple un filtre de Kalman pour estimer une constante [16]. Cependant, je préfère Python et j'ai opté pour l'option [16] avec une documentation complète. Je vais donner une description de l'algorithme:

Puisque la constante est toujours un modèle du système peut être représenté comme:

$$$x_ {k} = x_ {k-1} + w_ {k}$ , (1)

Pour le modèle, la matrice de transition dégénère en unité et la matrice de contrôle en zéro. Le modèle de mesure prend la forme:

$$$y_ {k} = y_ {k-1} + v_ {k}$ , (2)

Pour le modèle (2), la matrice de mesure est convertie en unité et la matrice de covariance $$$P, Q, R$ se transformer en dispersions. $$$k$ -ème étape, avant l'arrivée des résultats de mesure, le filtre scalaire de Kalman essaie d'évaluer le nouvel état du système en utilisant la formule (1):

$$$\ hat {x} _ {k / (k-1)} = \ hat {x} _ {(k-1) / (k-1)}$ , (3)

L'équation (3) montre que l'estimation a priori à l'étape suivante est égale à l'estimation postérieure faite à l'étape précédente. Estimation a priori de la variance de l'erreur:

$$$P_ {k / (k-1)} = P _ {(k-1) / (k-1)} + Q_ {k}$ , (4)

Selon une évaluation a priori de l'État $$$\ chapeau {x} _ {k / (k-1)}$ il est possible de calculer la prévision de mesure:

$$$\ hat {y} _ {k} = \ hat {x} _ {k / (k-1)}$ , (5)

Après la réception de la prochaine mesure $$$y_ {k}$ , le filtre calcule l'erreur de sa prévision $$$k$ e mesure:

$$$e_ {k} = y_ {k} - \ hat {y} _ {k} = y_ {k} - \ hat {x} _ {k / (k-1)}$ , (6)

Le filtre ajuste son évaluation de l'état du système, en choisissant un point situé quelque part entre l'évaluation initiale $$$\ chapeau {x} _ {k / (k-1)}$ et le point correspondant à la nouvelle dimension $$$y_ {k}$ :

$$$e_ {k} = y_ {k} - \ hat {y} _ {k} = y_ {k} - \ hat {x} _ {k / (k-1)}$ , (7)

où $$$G _ {k}$ - gain de filtre.

L'estimation de la variance d'erreur est également corrigée:

$$$P_ {k / (k)} = (1-G_ {k}) \ cdot P_ {k / (k-1)}$ , (8)

On peut prouver que la variance de l'erreur $$$e_ {k}$ est égal à:

$$$S_ {k} = P_ {k / (k-1)} + R_ {k}$ , (9)

Le gain du filtre, auquel l'erreur minimale dans l'évaluation de l'état du système est atteinte, est déterminé à partir de la relation:

$$$G_ {k} = P_ {k / (k-1)} / S_ {k}$ , (10)

Minimisation des erreurs d'entropie FC pour le bruit avec distribution de Cauchy, Pareto et gaussienne

1. En théorie des probabilités, la densité de distribution de Cauchy est déterminée à partir de la relation:

$$$f (x) = \ frac {b} {\ pi \ cdot (1-x ^ {2})}$

Pour cette distribution, il est impossible d'estimer l'erreur par les méthodes de la théorie des probabilités ( $$$\ sigma = \ infty$ ) mais la théorie de l'information vous permet de faire ceci:




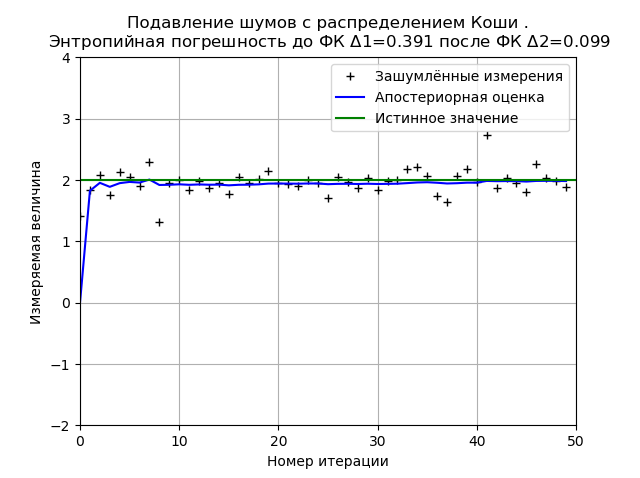
Le type du graphique peut changer à la fois au redémarrage du programme (nouvelle génération de l'échantillon de distribution) et en fonction du nombre de mesures et de paramètres de distribution, mais l'un reste inchangé. Le FC minimise la valeur de l'erreur d'entropie calculée sur la base de la théorie de l'information des mesures. Pour le graphique donné, FC réduit l'erreur d'entropie de 3,9 fois.

2. En théorie des probabilités, la densité de distribution de Pareto avec des paramètres $$$x_ {m}$ et $$$k$ déterminé à partir du rapport:

$$

$$f_ {X} (x) = \ left \ {\ begin {matrix} \ frac {kx_ {k} ^ {m}} {x ^ {k + 1}}, & x \ geq x_ {m} \\ 0, & x <x_ {m} \ end {matrice} \ droite.$$

Il convient de noter que la distribution de Pareto ne se trouve pas seulement dans l'économie. Vous pouvez donner l'exemple suivant de la distribution de la taille du fichier dans le trafic Internet via le protocole TCP.

3. En théorie des probabilités, la densité de la distribution normale (gaussienne) avec une attente mathématique $$$\ mu$ et écart type $$$\ sigma$ déterminé à partir du rapport:

$$$f (x) = \ frac {1} {\ sigma \ sqrt {2 \ pi}} \ cdot e ^ {- \ frac {(x- \ mu) ^ {2}} {2 \ sigma ^ {2} }}$

La détermination de la minimisation de l'erreur d'entropie FC du bruit avec une distribution gaussienne est donnée pour comparaison avec les distributions de Cauchy et Pareto non gaussiennes.




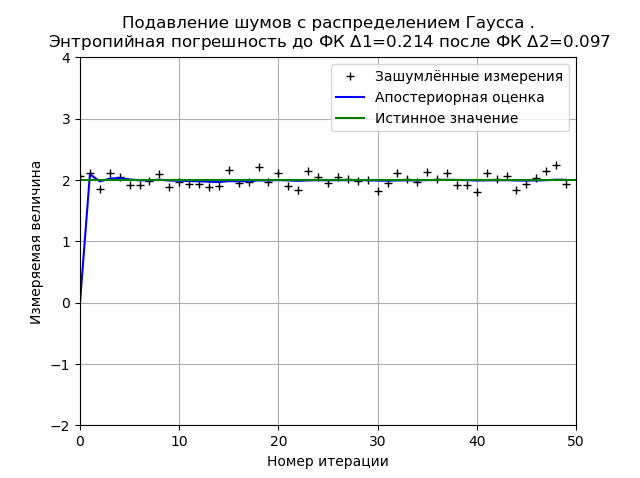
La distribution gaussienne fournit une stabilité plus élevée du résultat pour 50 mesures et pour le graphique montré, l'erreur d'entropie diminue de 2,2 fois.

Minimisation de l'erreur d'entropie FC à partir d'un échantillon de données expérimentales avec une loi de distribution de bruit inconnue




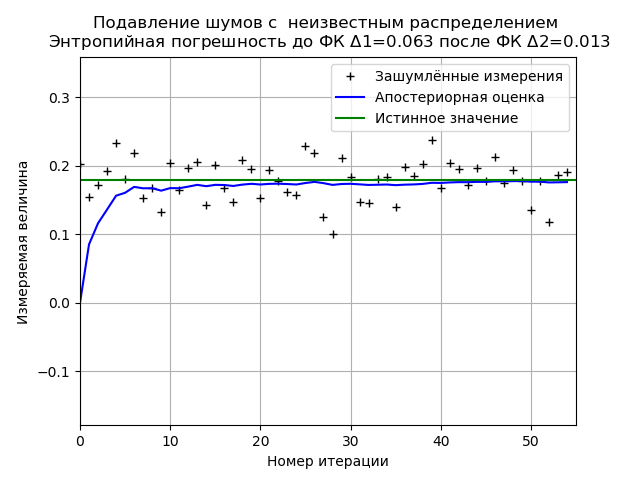
Lors de l'analyse d'un échantillon de données expérimentales, nous obtenons des résultats stables sur la minimisation de l'erreur d'entropie FC. Pour cet échantillon, le FC réduit l'erreur d'entropie de 4,85 fois.

Conclusion

Toutes les comparaisons de cet article ont été effectuées sur des échantillons de données limités, par conséquent, les conclusions fondamentales doivent être évitées, cependant, l'utilisation de l'erreur d'entropie nous permet de quantifier l'efficacité du filtre de Kalman dans la mise en œuvre donnée, par conséquent, la tâche de formation de cet article peut être considérée comme terminée.