Estimation de l'orientation spatiale, ou Comment ne pas avoir peur des filtres Mahoney et Majwik

De quoi parle-t-on

L'apparition sur Habre d'un article sur le filtre Majwik était dans son propre événement symbolique. Apparemment, l'enthousiasme général pour les drones a ravivé l'intérêt pour la tâche d'évaluer l'orientation du corps par des mesures inertielles. Dans le même temps, les méthodes traditionnelles basées sur le filtre de Kalman ont cessé de satisfaire le public - soit en raison des exigences élevées en ressources informatiques inacceptables pour les drones, soit en raison des paramètres complexes et peu intuitifs.

Le message était accompagné d'une mise en œuvre très compacte et efficace du filtre sur C. Cependant, à en juger par les commentaires, la signification physique de ce code, ainsi que l'article entier, est resté vague pour quelqu'un. Eh bien, nous admettons honnêtement: le filtre Majwik est le plus complexe du groupe de filtres basé en général sur des principes très simples et élégants. J'examinerai ces principes dans mon message. Le code ne sera pas là. Mon article n'est pas une histoire sur une implémentation spécifique de l'algorithme d'estimation d'orientation, mais plutôt une invitation à inventer vos propres variations sur un sujet donné, ce qui peut être beaucoup.

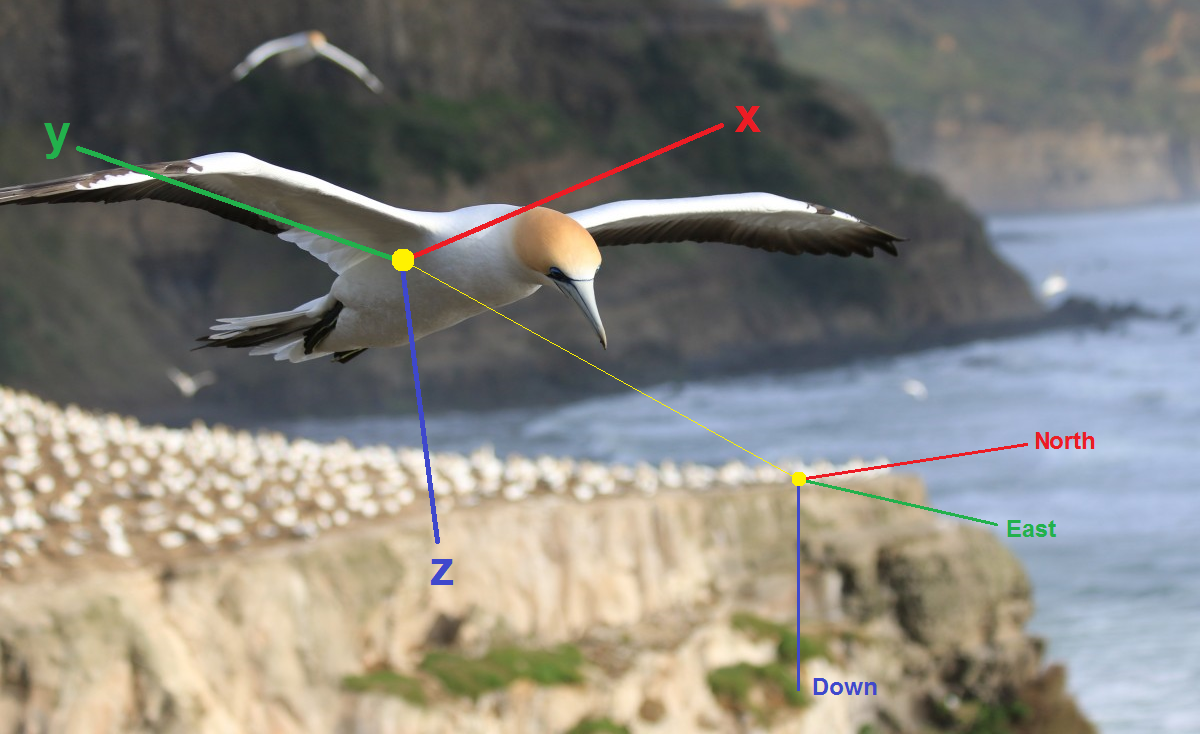
Vue d'orientation

Rappelez-vous les bases. Pour évaluer l'orientation du corps dans l'espace, vous devez d'abord sélectionner certains paramètres qui déterminent ensemble de manière unique cette orientation, à savoir essentiellement l'orientation du système de coordonnées associé $$$xyz$ système relativement conditionnellement fixe - par exemple, le système géographique NED (Nord, Est, Bas). Ensuite, vous devez faire des équations cinématiques, c'est-à-dire exprimer le taux de changement de ces paramètres à travers la vitesse angulaire des gyroscopes. Enfin, il faut introduire des mesures vectorielles à partir d'accéléromètres, de magnétomètres, etc. dans le calcul. Voici les façons les plus courantes de représenter l'orientation:

Angles d'Euler - roulis (roulis, $$$\ phi$ ), pitch (pitch, $$$\ theta$ ), cours (rubrique, $$$\ psi$ ) Il s'agit de l'ensemble de paramètres d'orientation le plus intuitif et le plus concis: le nombre de paramètres est exactement égal au nombre de degrés de liberté en rotation. Pour ces angles, nous pouvons écrire les équations cinématiques d'Euler . Ils sont très friands de mécanique théorique, mais dans les problèmes de navigation ils sont de peu d'utilité. Tout d'abord, la connaissance des angles ne permet pas de convertir directement les composantes d'un vecteur quelconque d'un connecté à un système de coordonnées géographiques ou vice versa. Deuxièmement, à un pas de ± 90 degrés, les équations cinématiques dégénèrent, le roulis et la course deviennent indéfinis.

Matrice de rotation - Matrice $$$\ mathbf {C}$ Taille 3 × 3, par laquelle vous devez multiplier n'importe quel vecteur dans le système de coordonnées associé pour obtenir le même vecteur dans le système géographique: $$$\ mathbf {r} _ {NED} = \ mathbf {C} \ mathbf {r} _ {xyz}$ . La matrice est toujours orthogonale, c'est-à-dire $$$\ mathbf {C} = \ mathbf {C} ^ {T}$ . L'équation cinématique pour elle a la forme $$$\ dot {\ mathbf {C}} = \ mathbf {C} \ mathbf {\ Omega}$ .
Ici $$$\ mathbf {\ Omega}$ - une matrice de composantes de vitesse angulaire mesurées par des gyroscopes dans un système de coordonnées connecté:

$$

$$\ mathbf {\ Omega} = \ begin {bmatrix} 0 & - \ omega_ {z} & \ omega_ {y} \\ \ omega_ {z} & 0 & - \ omega_ {x} \\ - \ omega_ {y } & \ omega_ {x} & 0 \\ \ end {bmatrix}$$

La matrice de rotation est légèrement moins évidente que les angles d'Euler, mais contrairement à eux, elle vous permet de convertir directement des vecteurs et ne perd pas de sens à n'importe quelle position angulaire. D'un point de vue informatique, son principal inconvénient est la redondance: pour trois degrés de liberté, neuf paramètres sont introduits en même temps, et tous doivent être mis à jour selon l'équation cinématique. Le problème peut être légèrement simplifié en utilisant l'orthogonalité de la matrice.

Le quaternion de rotation est un remède radical mais très peu intuitif contre la redondance et la dégénérescence. Il s'agit d'un objet à quatre composants. $$$\ mathbf {q} = q_ {0} + q_ {1} \ mathbf {i} + q_ {2} \ mathbf {j} + q_ {3} \ mathbf {k}$ - pas un nombre, pas un vecteur et pas une matrice. Le quaternion peut être vu sous deux angles. Tout d'abord, que diriez-vous de la quantité formelle du scalaire $$$q_ {0}$ et vecteur $$$q_ {1} \ mathbf {i} + q_ {2} \ mathbf {j} + q_ {3} \ mathbf {k}$ où $$$\ mathbf {i}, \ mathbf {j}, \ mathbf {k}$ - vecteurs d'axe unitaire (qui, bien sûr, semblent absurdes). Deuxièmement, comme une généralisation des nombres complexes, où maintenant nous utilisons non pas une, mais trois unités imaginaires différentes $$$\ mathbf {i}, \ mathbf {j}, \ mathbf {k}$ (ce qui ne semble pas moins absurde). Comment un quaternion est-il lié à un virage? Grâce au théorème d'Euler: un corps peut toujours être transféré d'une orientation donnée à une autre avec une rotation finie sous un certain angle $$$\ alpha$ autour d'un axe avec un vecteur de guidage $$$\ mathbf {u}$ . Ces angle et axe peuvent être combinés en un quaternion: $$$\ mathbf {q} = \ mathrm {cos} (\ alpha / 2) + \ mathbf {u} \ mathrm {sin} (\ alpha / 2)$ . Comme une matrice, un quaternion peut être utilisé pour convertir directement n'importe quel vecteur d'un système de coordonnées à un autre: $$$\ mathbf {r} _ {NED} = \ mathbf {q} \ mathbf {r} _ {xyz} {\ mathbf {q}} ^ {- 1}$ . Comme vous pouvez le voir, la représentation quaternionnelle de l'orientation souffre également de redondance, mais beaucoup moins que la matrice: un paramètre supplémentaire n'en est qu'un. La revue complète des quaternions était déjà sur Habré . Ils ont parlé de géométrie et de graphiques 3D. Nous nous intéressons également à la cinématique, car la vitesse de changement du quaternion doit être liée à la vitesse angulaire mesurée. L'équation cinématique correspondante a la forme $$$\ dot {\ mathbf {q}} = 1/2 \ mathbf {q} \ mathbf {\ omega}$ où est le vecteur $$$\ mathbf {\ omega}$ également considéré comme un quaternion avec une partie scalaire nulle.

Schémas de filtrage

L'approche la plus naïve du calcul de l'orientation consiste à s'armer d'une équation cinématique et à mettre à jour conformément à elle tout ensemble de paramètres que nous aimons. Par exemple, si nous avons choisi une matrice de rotation, nous pouvons écrire un cycle avec quelque chose dans l'esprit de C += * Omega * dt . Le résultat décevra. Les gyroscopes, en particulier les MEMS, ont des décalages d'origine importants et instables - en conséquence, même au repos complet, l'orientation calculée aura une erreur d'accumulation illimitée (dérive). Toutes les astuces inventées par Mahoney, Majwick et bien d'autres, sans m'exclure, visaient à compenser cette dérive en impliquant des mesures à partir d'accéléromètres, de magnétomètres, de récepteurs GNSS, de retards, etc. Ainsi toute une famille de filtres d'orientation est née, basée sur un principe de base simple.

Principe de base. Pour compenser la dérive d'orientation, il est nécessaire d'ajouter à la vitesse angulaire mesurée par les gyroscopes une vitesse angulaire de contrôle supplémentaire construite sur la base des mesures vectorielles d'autres capteurs. Le vecteur de vitesse angulaire de contrôle doit s'efforcer de combiner les directions des vecteurs mesurés avec leurs directions réelles connues.

Une approche complètement différente est adoptée ici que pour construire le terme de correction du filtre de Kalman. La principale différence est que la vitesse angulaire de contrôle n'est pas un terme, mais un facteur pour la valeur estimée (matrice ou quaternion). Des avantages importants en découlent:

• Un filtre d'évaluation peut être construit pour l'orientation elle-même, et non pour de petites déviations de l'orientation par rapport à celle fournie par les gyroscopes. De plus, les valeurs estimées satisferont automatiquement toutes les exigences que la tâche impose: la matrice sera orthogonale, le quaternion normalisé.
• La signification physique de la vitesse angulaire de contrôle est beaucoup plus claire que le terme de correction dans le filtre de Kalman. Toutes les manipulations sont effectuées avec des vecteurs et des matrices dans un espace physique tridimensionnel ordinaire, et non dans un espace d'état multidimensionnel abstrait. Cela simplifie considérablement le raffinement et le réglage du filtre, et en prime, il vous permet de vous débarrasser des matrices de grande dimension et des bibliothèques de matrices lourdes.

Voyons maintenant comment cette idée est implémentée dans des options de filtre spécifiques.

Filtre Mahoney. Toutes les mathématiques furieuses de l' article Mahoney original ont été écrites pour justifier des équations simples (32). Nous les réécrivons dans notre notation. Si nous ignorons l'estimation des déplacements nuls des gyroscopes, il reste alors deux équations clés - l'équation cinématique pour la matrice de rotation elle-même (avec la vitesse angulaire de contrôle sous la forme d'une matrice $$$\ mathbf {\ Omega} '$ ) et la loi de la formation de cette même vitesse sous la forme d'un vecteur $$$\ mathbf {\ omega} '$ . Pour simplifier, nous supposons qu'il n'y a pas d'accélérations ou de capteurs magnétiques, et grâce à cela, des mesures d'accélération en chute libre sont à notre disposition. $$$- \ hat {\ mathbf {g}} _ {xyz}$ des accéléromètres et du champ magnétique de la Terre $$$\ hat {\ mathbf {m}} _ {xyz}$ des magnétomètres. Les deux vecteurs sont mesurés par des capteurs dans un système de coordonnées connecté, et dans le système géographique, leur position est connue: $$$- \ mathbf {g} _ {NED}$ pointant vers le haut $$$\ mathbf {m} _ {NED}$ - au nord magnétique. Ensuite, les équations du filtre Mahoney ressembleront à ceci:

$$

$$\ dot {\ mathbf {C}} = \ mathbf {C} (\ mathbf {\ Omega} + \ mathbf {\ Omega} ') \\ \ mathbf {\ omega'} = k_ {g} \ hat {\ mathbf {g}} _ {xyz} \ times \ mathbf {C} ^ {T} \ mathbf {g} _ {NED} + k_ {m} \ hat {\ mathbf {m}} _ {xyz} \ times \ mathbf {C} ^ {T} \ mathbf {m} _ {NED}$$

Regardons attentivement la deuxième équation. Le premier terme à droite est un produit vectoriel. Le premier facteur est l'accélération mesurée de la gravité, le second est vrai. Étant donné que les facteurs doivent être dans un système de coordonnées, le deuxième facteur est converti en un système connecté en multipliant par $$$\ mathbf {C} ^ {T}$ . La vitesse angulaire, construite comme un produit vectoriel, est perpendiculaire au plan des vecteurs facteurs. Il vous permet de faire pivoter la position estimée du système de coordonnées associé jusqu'à ce que les vecteurs de facteur coïncident dans la direction - puis le produit vectoriel sera remis à zéro et la rotation s'arrêtera. Coefficient $$$k_ {g}$ définit la rigidité de cette rétroaction. Le deuxième terme effectue une opération similaire avec un vecteur magnétique. En fait, le filtre Mahoney incarne la thèse bien connue: la connaissance de deux vecteurs non colinéaires dans deux systèmes de coordonnées différents vous permet de restaurer uniquement l'orientation mutuelle de ces systèmes. S'il y a plus de deux vecteurs, cela fournira une redondance de mesure utile. S'il n'y a qu'un seul vecteur, alors un degré de liberté rotationnel (mouvement autour de ce vecteur) ne peut pas être fixé. Par exemple, si seul un vecteur est donné $$$- \ mathbf {g}$ , vous pouvez alors ajuster la dérive du roulis et du tangage, mais pas le cap.

Bien sûr, le filtre Mahoney n'a pas besoin d'utiliser une matrice de rotation. Il existe également des variantes de quaternion non canoniques.

Plate-forme gyroscopique virtuelle. Dans le filtre Mahoney, nous avons appliqué la vitesse angulaire de contrôle $$$\ mathbf {\ omega '}$ au système de coordonnées associé. Mais vous pouvez l'appliquer à la position estimée du système de coordonnées géographiques. L'équation cinématique prend alors la forme

$$

$$\ dot {\ mathbf {C}} = \ mathbf {C} \ mathbf {\ Omega} - \ mathbf {\ Omega} '\ mathbf {C}$$

Il s'avère que cette approche ouvre la voie à des analogies physiques très fructueuses. Il suffit de rappeler avec quoi la technique gyroscopique a commencé - les systèmes de navigation verticaux et inertiels basés sur la plate-forme gyrostabilisée dans un cardan.


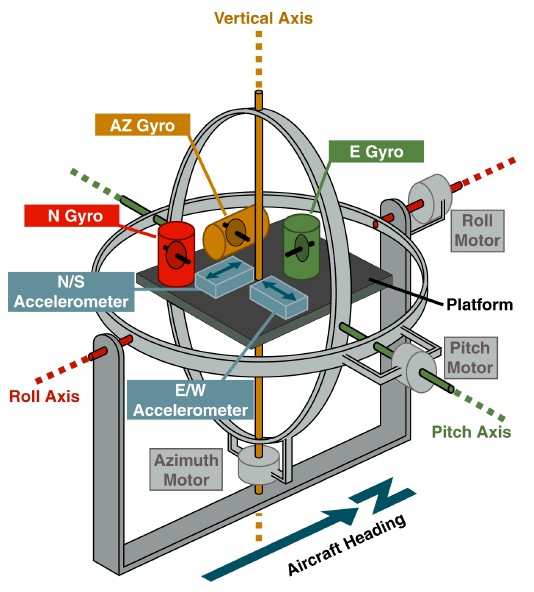www.theairlinepilots.com

L'objectif de la plateforme était la matérialisation du système de coordonnées géographiques. L'orientation du support a été mesurée par rapport à cette plate-forme par des capteurs d'angle sur les cadres de suspension. Si les gyroscopes avaient une dérive, la plate-forme a également dérivé après eux et des erreurs se sont accumulées dans les lectures des capteurs d'angle. Pour éliminer ces erreurs, une rétroaction a été introduite par les accéléromètres installés sur la plate-forme. Par exemple, la déviation de la plate-forme de l'horizon autour de l'axe nord a été perçue par l'accéléromètre de l'axe est. Ce signal a permis de régler la vitesse angulaire de contrôle $$$\ mathbf {\ omega '}$ renvoyant la plate-forme à l'horizon.

Nous pouvons utiliser les mêmes concepts visuels dans notre tâche. L'équation cinématique décrite doit alors être lue comme suit: le taux de changement d'orientation est la différence entre deux mouvements de rotation - le mouvement absolu du porteur (le premier terme) et le mouvement absolu de la plate-forme gyroscopique virtuelle (le deuxième terme). L'analogie peut être étendue à la loi de formation de la vitesse angulaire de contrôle. Vecteur $$$- \ hat {\ mathbf {g}} _ {NED} = - \ mathbf {C} \ hat {\ mathbf {g}} _ {xyz}$ Il représente le témoignage d'accéléromètres, soi-disant debout sur une plate-forme gyroscopique. Ensuite, pour des raisons physiques, vous pouvez écrire:

$$

$$\ omega '_ {N} = - gk_ {g} \ hat {g} _ {E}, \; \ omega '_ {E} = gk_ {g} \ hat {g} _ {N}$$

Il serait possible d'arriver exactement au même résultat de manière formelle, en effectuant une multiplication vectorielle dans l'esprit du filtre Mahoney, mais maintenant non pas dans un système connecté, mais dans un système de coordonnées géographiques. Est-ce seulement nécessaire?

Le premier indice d'une analogie utile entre la navigation par plate-forme et la navigation inertielle par sangle apparaît, apparemment, dans l' ancien brevet de Boeing . Ensuite, cette idée a été activement développée par Salychev , et récemment - par moi aussi . Les avantages évidents de cette approche:

• La vitesse angulaire de contrôle peut être formée sur la base de principes physiques compréhensibles.
• Naturellement, les canaux horizontaux et directionnels, qui sont très différents dans leurs propriétés et leurs méthodes de correction, sont séparés. Dans le filtre Mahoney, ils sont mélangés.
• Il est commode de compenser l'effet des accélérations dues à l'utilisation de données GNSS, qui sont émises précisément dans des axes géographiques plutôt que connexes.
• Il est facile de généraliser l'algorithme au cas de la navigation inertielle de haute précision, où il est nécessaire de prendre en compte la forme et la rotation de la Terre. Comment faire cela dans le système Mahoney, je ne peux pas imaginer.

Filtre Majwick. Majwik a choisi la voie difficile . Si Mahoney, apparemment, est venu intuitivement à sa décision, et l'a ensuite justifiée mathématiquement, alors Majwik s'est révélé dès le début être un formaliste. Il s'est engagé à résoudre le problème d'optimisation. Il a raisonné comme ça. Définissez l'orientation du quaternion de rotation. Dans le cas idéal, la direction calculée d'un vecteur mesuré (ayons ceci $$$- \ mathbf {g}$ ) coïncide avec le vrai. Alors sera $$${\ mathbf {q}} ^ {- 1} \ mathbf {g} _ {NED} \ mathbf {q} = \ hat {\ mathbf {g}} _ {xyz}$ . En réalité, ce n'est pas toujours réalisable (surtout s'il y a plus de deux vecteurs), mais vous pouvez essayer de minimiser l'écart $$$\ mathbf {F} = {\ mathbf {q} ^ {- 1} \ mathbf {g} _ {NED} \ mathbf {q}} - \ hat {\ mathbf {g}} _ {xyz}$ de l'égalité exacte. Pour ce faire, nous introduisons le critère de minimisation

$$

$$E = \ frac {1} {2} | \ mathbf {F} | ^ {2} \ rightarrow \ mathrm {min}$$

La minimisation nécessite une descente de gradient - se déplaçant par petits pas dans la direction opposée au gradient $$$\ nabla E$ , c'est-à-dire opposé à l'augmentation de fonction la plus rapide $$$E$ . Soit dit en passant, Majwik fait une erreur: dans toutes ses œuvres, il ne présente pas $$$E$ et écrit avec insistance $$$\ nabla \ mathbf {F}$ au lieu de $$$\ nabla E$ , bien qu'il calcule exactement $$$\ nabla E$ .

En conséquence, la descente de gradient conduit à la condition suivante: pour compenser la dérive d'orientation, un nouveau terme négatif proportionnel à l'équation cinématique doit être ajouté à partir de l'équation cinématique $$$\ nabla E$ :

$$

$$\ dot {\ mathbf {q}} = \ frac {1} {2} \ mathbf {q} \ mathbf {\ omega} - \ beta \ frac {\ nabla E} {| \ nabla E |}$$

Ici Majwik s'écarte un peu de notre «principe de base»: il n'ajoute pas le terme de correction à la vitesse angulaire, mais au taux de variation du quaternion, et ce n'est pas exactement la même chose. En conséquence, il peut s'avérer que le quaternion mis à jour cesse d'être unique et, par conséquent, perd la capacité de représenter l'orientation. Par conséquent, pour le filtre Majwik, la normalisation artificielle du quaternion est une opération vitale, tandis que pour d'autres filtres, elle est souhaitable, non facultative.

L'effet de l'accélération

Jusqu'à présent, on a supposé qu'il n'y avait pas de véritables accélérations et les accéléromètres ne mesuraient que l'accélération gravitationnelle $$$- \ mathbf {g}$ . Cela a permis d'obtenir une norme verticale et, avec son aide, de compenser la dérive de roulis et de tangage. Cependant, dans le cas général, les accéléromètres, quel que soit leur principe de fonctionnement, mesurent l' accélération apparente - la différence vectorielle de l'accélération réelle et de l'accélération gravitationnelle $$$\ mathbf {f} = \ mathbf {a} - \ mathbf {g}$ . La direction de l'accélération apparente ne coïncide pas avec la verticale et les erreurs provoquées par les accélérations apparaissent dans les estimations de roulis et de tangage.

Ceci est facile à illustrer en utilisant l'analogie d'une plate-forme gyroscopique virtuelle. Son système de correction est conçu pour que la plate-forme s'arrête dans cette position angulaire dans laquelle les signaux des accéléromètres, supposément installés dessus, sont remis à zéro, c'est-à-dire lorsque le vecteur mesuré $$$\ mathbf {f}$ devient perpendiculaire aux axes de la sensibilité des accéléromètres. S'il n'y a pas d'accélération, cette position coïncide avec l'horizon. Lorsque des accélérations horizontales se produisent, la plate-forme gyroscopique est déviée. Nous pouvons dire que la plate-forme gyroscopique est similaire à un pendule ou à un fil à plomb fortement amorti.



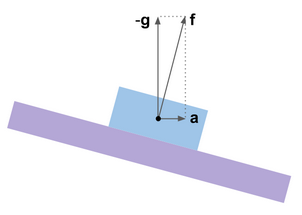
Dans les commentaires de l'article sur le filtre Majwik, une question s'est posée autour de savoir s'il était possible d'espérer que ce filtre est moins sensible aux accélérations que, par exemple, le filtre Mahoney. Hélas, tous les filtres décrits ici exploitent les mêmes principes physiques et souffrent donc des mêmes problèmes. Il est impossible de tromper la physique avec les mathématiques. Que faire alors?

Le moyen le plus simple et le plus difficile a été inventé au milieu du siècle dernier pour les gyrostaxies aéronautiques: réduire ou complètement mettre à zéro la vitesse angulaire de contrôle en présence d'accélérations ou la vitesse angulaire du parcours (qui indique l'entrée dans un virage). La même méthode peut être appliquée aux systèmes de plate-forme actuels. Dans ce cas, les accélérations doivent être jugées par les valeurs $$$\ hat {f} _ {N}, \ hat {f} _ {E}$ mais pas $$$\ hat {f} _ {x}, \ hat {f} _ {y}$ qui eux-mêmes sont nuls. Cependant en taille $$$\ hat {\ mathbf {f}} _ {NED}$ il n'est pas toujours possible de distinguer les vraies accélérations des projections d'accélération gravitationnelle, qui est due à l'inclinaison de la plate-forme gyroscopique, qui doit être éliminée. Par conséquent, la méthode ne fonctionne pas de manière fiable - mais elle ne nécessite aucun capteur supplémentaire.

Une méthode plus précise est basée sur l'utilisation de mesures de vitesse externes à partir du récepteur GNSS. Si la vitesse est connue $$$\ mathbf {v}$ , alors il peut être différencié numériquement et obtenir une véritable accélération $$$\ dot {\ mathbf {v}}$ . Alors la différence $$$\ hat {\ mathbf {f}} _ {NED} - \ dot {\ mathbf {v}}$ sera exactement égal $$$- \ hat {\ mathbf {g}} _ {NED}$ indépendamment du mouvement des médias. Il peut être utilisé comme standard de vertical. Par exemple, vous pouvez spécifier la vitesse angulaire de contrôle de la plate-forme gyroscopique sous la forme

$$

$$\ omega '_ {N} = gk_ {g} (\ hat {f} _ {E} - \ dot {v} _ {E}), \; \ omega '_ {E} = - gk_ {g} (\ hat {f} _ {N} - \ dot {v} _ {N})$$

Décalages d'origine du capteur

Une triste caractéristique des gyroscopes et des accéléromètres grand public est la grande instabilité du décalage zéro dans le temps et la température. Pour les éliminer, il ne suffit pas d'étalonner en usine ou en laboratoire - vous devez réévaluer pendant le fonctionnement.

Gyroscopes. Nous allons traiter zéro décalage des gyroscopes $$$\ delta {\ mathbf {\ omega}}$ . La position estimée du système de coordonnées associé s'éloigne de sa position réelle avec une vitesse angulaire déterminée par deux facteurs opposés - déplacements nulles des gyroscopes et contrôle de la vitesse angulaire: $$$\ delta {\ mathbf {\ omega}} - \ mathbf {\ omega '}$ . Si le système de correction (par exemple, dans le filtre Mahoney) a réussi à arrêter la sortie, alors à l'état stable, il sera $$$\ delta {\ mathbf {\ omega}} = \ mathbf {\ omega '}$ . En d'autres termes, dans la vitesse angulaire de contrôle $$$\ mathbf {\ omega '}$ informations sur une perturbation valide inconnue $$$\ delta {\ mathbf {\ omega}}$ . Par conséquent, une estimation compensatoire peut être appliquée: nous ne connaissons pas directement l'ampleur de la perturbation, cependant, nous savons quelle action corrective est nécessaire pour l'équilibrer. C'est la base pour estimer les déplacements nuls des gyroscopes. Par exemple, dans Mahoney, le score est mis à jour conformément à la loi

$$

$$\ dot {\ hat {\ delta \ mathbf {\ omega}}} = k_ {b} \ mathbf {\ omega '}$$

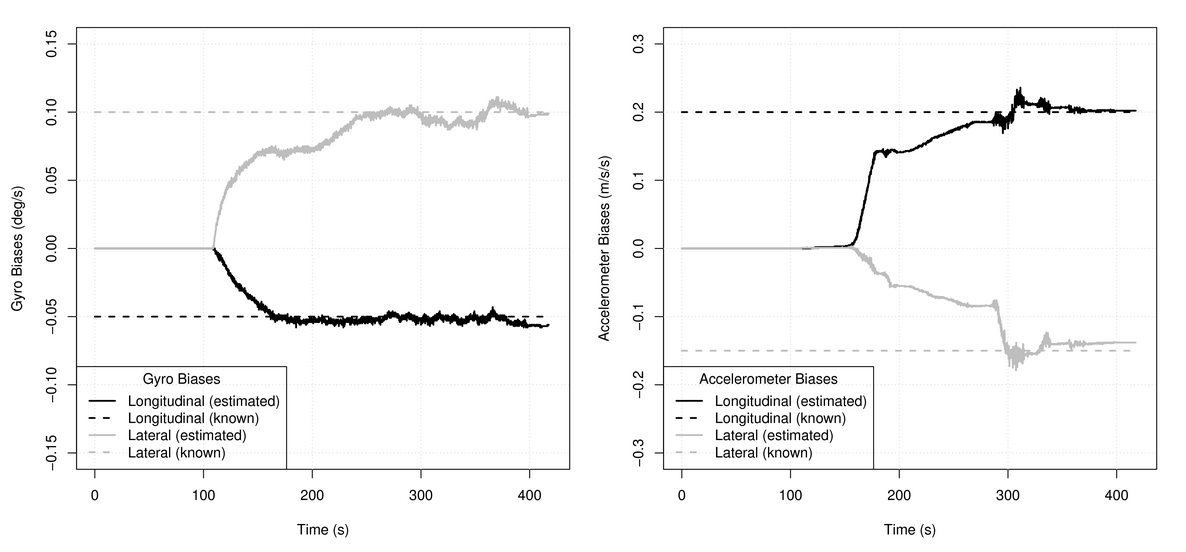
Cependant, le résultat est étrange: les estimations atteignent 0,04 rad / s. Une telle instabilité de zéro décalage ne se produit pas même dans les gyroscopes les plus méchants. Je soupçonne que le problème est que Mahoney n'utilise pas GNSS ou d'autres capteurs externes - et est entièrement affecté par l'influence des accélérations. Uniquement sur l'axe vertical, où l'accélération ne nuit pas, l'estimation semble plus ou moins robuste:


Mahony et al., 2008

Accéléromètres Accéléromètres à décalage zéro $$$\ delta {\ mathbf {f}}$ beaucoup plus difficile. Les informations les concernant doivent être extraites de la même vitesse angulaire de contrôle $$$\ mathbf {\ omega '}$ . Cependant, en mouvement rectiligne, l'effet des déplacements nuls des accéléromètres est indiscernable de l'inclinaison du support ou de l'inclinaison de l'installation du bloc capteur sur celui-ci. Aucun additif à $$$\ mathbf {\ omega '}$ les accéléromètres ne créent pas. L'additif n'apparaît que dans un virage, ce qui nous permet de séparer et d'évaluer indépendamment les erreurs des gyroscopes et des accéléromètres. Un exemple de la façon dont cela peut être fait est dans mon article . Voici les photos de là:

Au lieu d'une conclusion: qu'en est-il du filtre de Kalman?

Je ne doute pas que les filtres décrits ici auront presque toujours un avantage sur le filtre Kalman traditionnel en termes de vitesse, de compacité du code et de facilité de configuration - pour cela, ils ont été créés. Quant à l'exactitude de l'évaluation, ici tout n'est pas si clair. J'ai rencontré des filtres Kalman conçus sans succès, qui en termes de précision étaient nettement inférieurs à un filtre avec une plate-forme gyroscopique virtuelle. Majwik a également prouvé les avantages de son filtre par rapport à certaines estimations de Kalman. Cependant, pour la même tâche d'estimation de l'orientation, vous pouvez créer au moins une douzaine de circuits de filtre Kalman différents, et chacun aura d'innombrables paramètres. Je n'ai aucune raison de penser que le filtre Mahoney ou Majwik sera plus précis que le meilleur filtre Kalman possible . Et bien sûr, l'approche de Kalman aura toujours l'avantage de l'universalité: elle n'impose aucune restriction stricte aux propriétés dynamiques spécifiques du système évalué.