Partie 2. Carburant très lourd
Partie précédente 1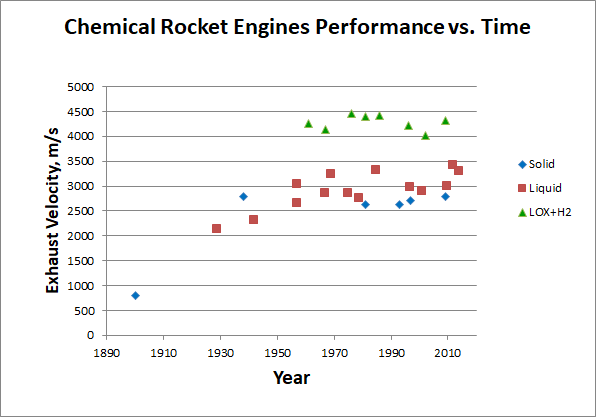
Devant vous se trouve la Station spatiale internationale. Avec une masse de 420 tonnes et une valeur de
[ 20 ] de 150 milliards de dollars:

Son énergie cinétique, le bon vieux
E =
mv 2/2 , est de 1,3 * 10
13 joules. En ajoutant de l'énergie potentielle à une altitude de 400 kilomètres, nous obtenons 1,4 * 10
13 J.
De combien de gaz avez-vous besoin pour brûler pour obtenir cette énergie? Il s'avère que ce n'est pas tellement. 350 tonnes au total. C'est approximativement le
[ 200 ] budget énergétique d'une journée d'Ulan-Ude.
Comment se fait-il que, loin de la ville la plus riche du monde en une seule journée, elle gère suffisamment d'énergie pour accélérer l'ISS à la vitesse orbitale, cependant, nous avons une station pour le monde entier, et cela coûte de l'argent indécemment fou?
La réponse
réside dans l' évidence de l'anatomie du lanceur.
Le transporteur doit au minimum inclure:
- Charge utile. Sinon, pourquoi est-il nécessaire?
- Au moins un moteur.
- Un boîtier qui relie tout cela.
- Et, bien sûr, le carburant. Comme fluide de travail et, dans la plupart des cas, comme source d'énergie.
Et dans le dernier paragraphe, le problème est enraciné. Pour soulever et traîner un certain minimum de carburant, il vous faut ... correctement, du carburant supplémentaire! A la montée de laquelle vous avez également besoin de carburant! Et cet emballage dure longtemps. Bien sûr, il converge, sinon nous ne volerions nulle part. Mais selon les résultats de la convergence, une fusée moderne, voire multi-étages, voire de haute qualité conçue et exécutée, en masse se compose principalement de ce même carburant.
Eh bien, voici un exemple de manuel, Saturne V n'est pas le plus récent, mais l'un des missiles les plus efficaces de l'histoire
[ 30 ] :

[Image originale de l'histoire de la NASA [
40 ]]
Poids de départ - 2970 tonnes. Quelque 2670 d'entre eux sont du carburant. Dont 2160 brûlent en moins de trois minutes de toute l'expédition lunaire. Malgré le fait que l'énergie cinétique de la charge utile en orbite «ne coûte» que 100 tonnes de carburant.
Il s'avère que la principale difficulté à entrer en orbite n'est pas un manque d'énergie. Ses terriens ont suffisamment d'énergie cinétique non seulement pour les stations, mais aussi pour les navires de croisière en orbite. Le problème est différent: notre carburant est trop lourd. Il en faut trop en kilogrammes pour collecter la quantité d'énergie nécessaire au vol. Pourquoi la majeure partie du carburant versé dans la fusée irait-elle au transport du carburant? En fait, la formule de Tsiolkovsky, reliant le
M de départ et la masse finale de la fusée
m avec la vitesse
V et la vitesse d'échappement du moteur
u , nous dit la même chose:
M /
m = e
V / u [2]
À première vue, ce n'est pas tout à fait évident qu'est-ce que le contenu énergétique par kilogramme a à voir avec cela? Mais tout est simple. Il "siège" en
u , au rythme de l'expiration. Pour le carburant chimique, il est limité par (et à une première approximation égale à)
u = √ (2
q ), où
q est la chaleur spécifique de combustion. Quel est le contenu énergétique par kilogramme. Et lorsque ce
q «tombe en deçà», le rapport de masse au départ et à l'arrivée se révèle être exponentiellement énorme:
M /
m = e
V / √ (2 q ) [3]
Ou
V = Ln (
M /
m ) * √ (
2q ) [3a]
Quelques notes, pour les nerds et pour la clarté1. Oui, il existe des expressions plus précises du débit que
u = √ (
2q ). Quand je leur ai accordé le crédit, Gorbatchev a "remis" l'URSS. Mais ces formules sont compliquées, effrayent les lecteurs et prennent en compte des effets qui ne sont pas importants ici.
u = √ (
2q ), bien qu'il surestime la réponse de 10 à 30%, décrit adéquatement la dépendance qui nous intéresse. Et oui, il existe une impulsion spécifique, mais dans cet article particulier, le débit est plus pratique à utiliser.
2. En principe, rien n'interdit même à une fusée chimique d'obtenir une vitesse de sortie
u supérieure à √ (2
q ). Comment? Eh bien, disons, pour brûler du carburant non pas dans une buse, mais dans un générateur, générant de l'énergie électrique. Ensuite, avec cette énergie, accélérez la fraction
x de l' échappement (0 <
x ≤ 1) à des vitesses très élevées. Par exemple, un turboréacteur à plasma électrique
[ 230 ] . Et les résidus d'échappement sont stupidement déversés à vitesse nulle. Pour simplifier, nous supposons que toutes les transformations se produisent sans perte d'énergie, avec une efficacité de 100%. Une telle fusée accélérera-t-elle à une vitesse plus élevée
V avec un rapport de masse fixe
M /
m (c'est-à-dire, sera-t-elle plus efficace)?
La réponse est non. Il est facile de résoudre les équations décrivant le mouvement d'une telle fusée et d'obtenir:
V = Ln (
M /
m ) * √ (
2qx )
C'est-à-dire sa vitesse finale ne sera que de √
x par rapport à la fusée «ordinaire» typée à combustion directe (cf. [3a]). Et cette vitesse est toujours rigidement liée à
q .
3. Que faire si la fusée ne fonctionne pas avec du carburant, mais avec une batterie? Eh bien, qu'il y ait un support de travail séparé de masse
m f à bord et séparément une batterie avec une réserve d'énergie
E et une masse
m b .
La première chose que vous devez comprendre ici est que la batterie doit être constituée de nombreux petits «modules» qui sont réinitialisés au fur et à mesure qu’ils fonctionnent. Sinon, nous emporterons avec nous la charge «morte» de batteries vides. Mais si c'est le cas, alors conceptuellement, cela n'est pas différent du carburant ordinaire à bord avec une réserve d'énergie totale
E et une masse
m f +
m b . Et si
q =
E / (
m f +
m b ) d'un tel système est inférieur à celui d'une fusée chimique conventionnelle, il ne s'envolera pas mieux.
5. Mais qu'en est-il des moteurs-fusées électriques
[ 225 ] ? Après tout, ils donnent des débits de dizaines et de centaines de kilomètres par seconde, et ils ont effectué des manœuvres interplanétaires réussies avec des rapports
M /
m très modestes. Comment ça? Le fait est que les ERD sont des systèmes ouverts. Ils transportent le fluide de travail (mercure, xénon, etc.) avec eux. Mais l'énergie ne l'est pas. L'énergie provient de panneaux solaires. Si au contraire ils transportaient des batteries ordinaires avec un contenu énergétique de masse
q , alors leur efficacité ne serait pas plus élevée, selon la formule [3a].
L'article a été écrit pour le site https://habr.com . Lors de la copie, veuillez vous référer à la source. L'auteur de l'article est Evgeny Bobukh .Ainsi, les missiles sont chers parce que leur conception "sèche" extrêmement légère est obligée de résister à une charge extrêmement lourde, principalement du carburant (et même de la "pomper" rapidement à travers le TNA). Et la charge est grande car notre carburant est trop lourd. On y place très peu de joules par kilogramme.
Comprenons maintenant les raisons de cette limitation.
Pourquoi regarder de plus près la réaction de la combustion de l'hydrogène dans le fluor, l'une des plus simples. Dans ce document, les paires hydrogène-hydrogène et fluor-fluor échangent des partenaires, créant deux paires hydrogène-fluor:
H 2 +
F 2 = 2
HFD'où vient l'énergie libérée?
Une molécule d'hydrogène a deux atomes. Les atomes ont des électrons. Ils sont "étalés" autour de l'atome sous la forme d'une sorte de nuage, et sont connectés au noyau principalement par attraction électrostatique. Les électrons sont externes, valence et (sauf l'hydrogène) internes, ne participant pas aux réactions chimiques. Après la réaction, l'hydrogène et le fluor changent de place. Les nuages électriques d'électrons de valence sont redistribués et changent légèrement de forme. Quelque chose comme ça:
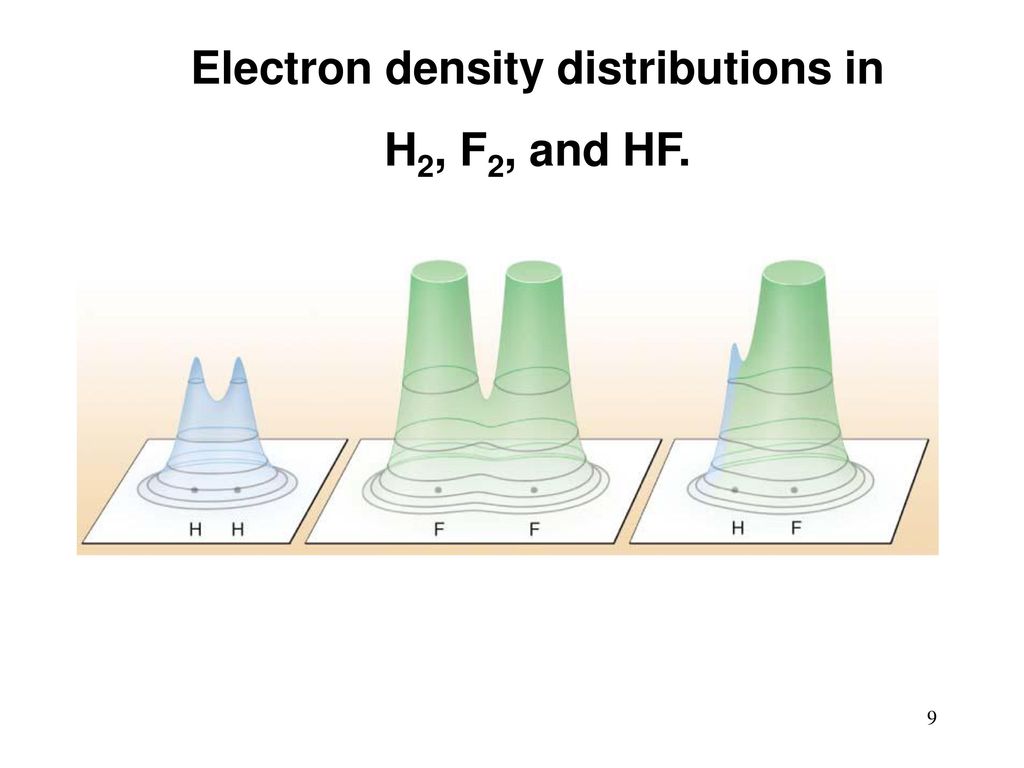
[Crédit d'image [
295 ]]
L'énergie potentielle de liaison des électrons avec les atomes dans les nouveaux nuages est différente. Dans ce cas (cette énergie est négative), elle est désormais inférieure à celle de
H 2 et
F 2 séparément. Où est passée la différence? L'énergie cinétique d'une molécule, les vibrations de ses atomes, le rayonnement électromagnétique. Tout cela s'est finalement transformé en chaleur. Ce qui a élargi le gaz et a donné une traction.
Et voici le moment critique. Seuls les électrons de valence externes sont impliqués dans les réactions chimiques. La distribution de densité des autres électrons (ainsi que le champ électrique «dans la profondeur» de l'atome) restent pratiquement inchangés. Dans les réactions chimiques, les atomes interagissent les uns avec les autres comme par des «intermédiaires», qui sont des électrons de valence:
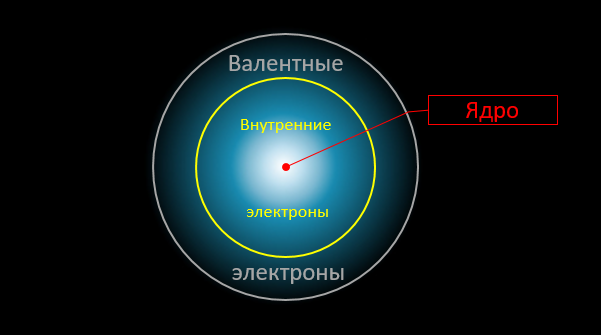
Maintenant, attention, la question est: quelle est l'énergie maximale possible qui peut être libérée pendant une telle «permutation»? Évidemment, il ne peut pas dépasser la somme des énergies de liaison des électrons externes avec les atomes (dans le produit final et initial). Mais ces énergies de liaison nous sont bien connues
[ 285 ] . Par atome, ils s'élèvent à 1,5 - 25
électron-volts (
eV ) et sont exprimés en fractions de la constante de Rydberg - une valeur fondamentale construite à partir des constantes de base de notre Univers:
Ry (dans le système gaussien) =
m e e 4/2 ħ 2 =
1 3 .6 eV [
300 ]
De plus, les 25 et 13,6 eV sont inaccessibles. Car dans des réactions typiques loin de toute l'énergie de liaison est libérée, mais seule sa différence entre les deux configurations, et donc le plafond pratique de la libération d'énergie de la chimie est de 3-4 eV par atome. En termes de kilogramme typique de carburant + comburant, cela équivaut à 20-30 MJ d'énergie libérée. C'est cette quantité qui définit la vitesse maximale théorique du gaz d'un moteur à réaction chimique à combustion directe
u = √ (2
q ) = √ (2 * 2,5 * 10
7 ) ≈ 7000 m / s. Inatteignable, bien sûr, car il ne prend pas en compte les pertes sur les degrés de liberté internes des molécules, la dissociation, le rayonnement, le mouvement thermique non directionnel, etc.
Il peut sembler que les chaleurs de combustion tabulaires
[ 240 ] (disons, 120 MJ / kg pour l'hydrogène) contredisent la figure écrite ci-dessus. Mais le fait est que ces chaleurs sont généralement indiquées par kilogramme de
carburant , sans tenir compte de l'oxydant nécessaire à sa combustion. La fusée transporte les deux composants avec elle, et si vous recalculez l'énergie libérée par kilogramme du
mélange (avec une combustion équilibrée), une image complètement différente émerge
[ 240 ] [ 250 ] [ 260 ] :
| Carburant + comburant | Réaction | Pouvoir calorifique par kg. carburant, MJ / kg | 1 kg de carburant a besoin d'un comburant, kg. | Pouvoir calorifique, MJ / kg | La sortie par atome du mélange, eV |
| Hydrogène + oxygène | 2H 2 + O 2 = 2H 2 O | 120 | 8 | 13,3 | 0,83 |
| Kérosène + oxygène | 2C 12 H 26 + 37O 2 = 24CO 2 + 26H 2 O | 43 | 3,5 | 9,6 | 1.02 |
| Charbon + oxygène | C + O 2 = CO 2 | 33 | 2.7 | 9.0 | 1,38 |
| Lithium + oxygène | 4Li + O 2 = 2Li 2 O | 43,5 | 1.2 | 20,2 | 2.10 |
| Bore + oxygène | 2B + 1,5O 2 = B 2 O 3 | 57,2 | 2.2 | 17,8 | 2,58 |
| Magnésium + oxygène | 2Mg + O 2 = 2MgO | 25,1 | 0,7 | 15,1 | 3.18 |
| Béryllium + oxygène | 2Be + O 2 = 2BeO | 66,6 | 1,8 | 24,0 | 3.12 |
| Lithium + fluor | 2Li + F 2 = 2LiF | 88,8 | 2.7 | 23,7 | 3.21 |
| Béryllium + fluorure | Be + F 2 = BeF 2 | 114 | 4.2 | 21,9 | 3,57 |
| Dicyanoacétylène + ozone | C 4 N 2 + (4/3) O 3 = 4 CO + N 2 | 16,2 | 0,8 | 8.8 | 1,28 |
Comme vous pouvez le voir, même les plus énergivores, bien que non adaptés à une utilisation pratique, les carburants ne fournissent que 24 MJ / kg de chaleur pendant la combustion. Et nous avons rencontré cette limite presque depuis le début de l'astronautique, qui montre un graphique du taux de sortie des moteurs chimiques en fonction de l'année de leur création:

[Premiers moteurs selon [
310 ], [
320 ], [
330 ], plus tard - Wikipedia individuellement. Collecte de données
ici ]
Il semble que le potentiel du carburant chimique soit développé depuis longtemps. Est-il possible de commencer à stocker de l'énergie sous une forme différente?
À suivre.Références et littérature