Compression de données Huffman

Entrée

Dans cet article, je parlerai de l'algorithme bien connu de Huffman, ainsi que de son application à la compression de données.

En conséquence, nous écrirons un simple archiveur. Il y avait déjà un article à ce sujet sur Habré , mais sans mise en œuvre pratique. Le matériel théorique du poste actuel est tiré des cours d'informatique scolaire et du livre de Robert Lafore «Structures de données et algorithmes en Java». Donc, tout est sous la coupe!

Une petite pensée

Dans un fichier texte brut, un caractère est codé sur 8 bits (codage ASCII) ou 16 (codage Unicode). De plus, nous considérerons le codage ASCII. Par exemple, prenez la ligne s1 = "SUSIE DIT QUE C'EST FACILE \ n". Au total, il y a bien sûr 22 caractères dans la ligne, y compris les espaces et le caractère de nouvelle ligne - '\ n'. Un fichier contenant cette ligne pèsera 22 * ​​8 = 176 bits. La question se pose immédiatement: est-il rationnel d'utiliser les 8 bits pour coder 1 caractère? Nous n'utilisons pas tous les caractères ASCII. Même s'il était utilisé, il serait plus rationnel que la lettre la plus fréquente - S - donne le code le plus court possible, et que la lettre la plus rare - T (ou U, ou '\ n') - donne un code plus authentique. Voici l'algorithme de Huffman: vous devez trouver la meilleure option d'encodage, dans laquelle le fichier aura un poids minimal. Il est tout à fait normal que les longueurs de code diffèrent pour différents caractères - c'est la base de l'algorithme.

Codage

Pourquoi ne pas donner au caractère 'S' un code, par exemple, 1 bit de long: 0 ou 1. Soit 1. Puis nous donnerons le deuxième caractère le plus rencontré - '' (espace) - 0. Imaginez, vous avez commencé à décoder votre message - chaîne codée s1 - et vous voyez que le code commence par 1. Alors que faire: est-ce un caractère S, ou est-ce un autre caractère, par exemple A? Par conséquent, une règle importante se pose:

Aucun code ne doit être le préfixe d'un autre

Cette règle est la clé de l'algorithme. Par conséquent, la création du code commence par le tableau des fréquences, qui indique la fréquence (nombre d'occurrences) de chaque caractère:

Les caractères avec le plus d'occurrences doivent être codés avec le plus petit nombre possible de bits. Je vais donner un exemple d'une des tables de code possibles:

Ainsi, le message codé ressemblera à ceci:

10 01111 10 110 1111 00 10 010 1110 10 00 110 0110 00 110 10 00 1111 010 10 1110 01110 

J'ai séparé le code de chaque caractère par un espace. Cela n'arrivera pas vraiment dans un fichier compressé!
La question se pose: comment cette salaga a-t-elle créé un code ? Comment créer une table de codes? Ceci sera discuté ci-dessous.

Construire un arbre huffman

Ici, les arbres de recherche binaires viennent à la rescousse. Ne vous inquiétez pas, ici les méthodes de recherche, d'insertion et de suppression ne sont pas nécessaires. Voici la structure arborescente en java:

 public class Node { private int frequence; private char letter; private Node leftChild; private Node rightChild; ... } 

 class BinaryTree { private Node root; public BinaryTree() { root = new Node(); } public BinaryTree(Node root) { this.root = root; } ... } 

Ce n'est pas un code complet, le code complet sera ci-dessous.

Voici l'algorithme de construction d'arbre lui-même:

1. Créez un objet Node pour chaque caractère du message (ligne s1). Dans notre cas, il y aura 9 nœuds (objets Node). Chaque nœud se compose de deux champs de données: symbole et fréquence
2. Créez un objet Tree (BinaryTree) pour chacun des nœuds Node. Le nœud devient la racine de l'arbre.
3. Collez ces arbres dans la file d'attente prioritaire. Plus la fréquence est basse, plus la priorité est élevée. Ainsi, lors de l'extraction, le dervo est toujours sélectionné avec la fréquence la plus basse.

Ensuite, vous devez effectuer les opérations suivantes de manière cyclique:

1. Extrayez deux arbres de la file d'attente prioritaire et faites-en les descendants du nouveau nœud (le nœud nouvellement créé sans lettre). La fréquence du nouveau nœud est égale à la somme des fréquences de deux arbres descendants.
2. Pour ce nœud, créez un arbre avec une racine dans ce nœud. Collez à nouveau cet arbre dans la file d'attente prioritaire. (Étant donné que l'arbre a une nouvelle fréquence, il est très probable qu'il atteindra un nouvel emplacement dans la file d'attente)
3. Continuez les étapes 1 et 2 jusqu'à ce qu'il ne reste qu'un seul arbre dans la file d'attente - l'arbre Huffman

Considérez cet algorithme sur la ligne s1:



Ici, le symbole «lf» (saut de ligne) indique la transition vers une nouvelle ligne, «sp» (espace) est un espace.

Et ensuite?

Nous avons obtenu un arbre Huffman. Et bien. Et qu'en faire? Ils ne le prendront pas gratuitement. Ensuite, vous devez suivre tous les chemins possibles de la racine aux feuilles de l'arbre. Convenons de désigner l'arête 0 si elle mène au descendant gauche et 1 si à la droite. A strictement parler, dans ces notations, le code symbole est le chemin de la racine de l'arbre à la feuille contenant ce même symbole.



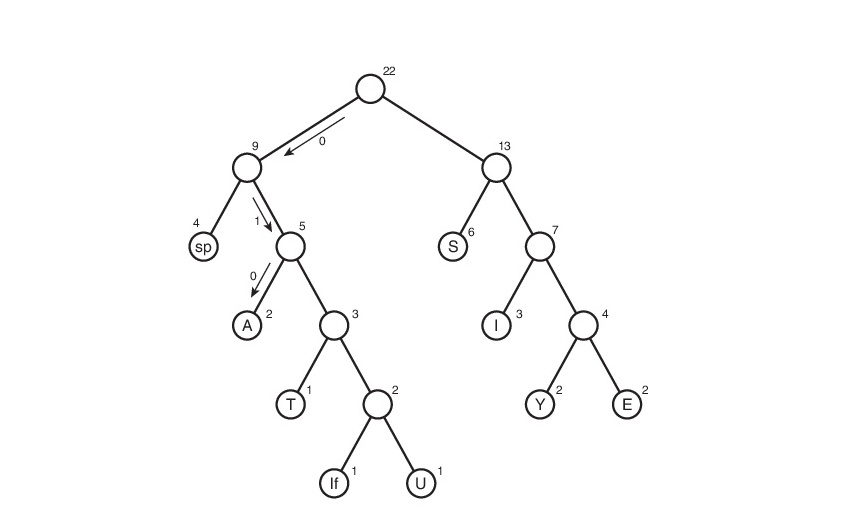
Ainsi, le tableau des codes s'est avéré. Notez que si nous considérons ce tableau, nous pouvons conclure sur le "poids" de chaque caractère - c'est la longueur de son code. Le fichier compressé pèsera alors: 2 * 3 + 2 * 4 + 3 * 3 + 6 * 2 + 1 * 4 + 1 * 5 + 2 * 4 + 4 * 2 + 1 * 5 = 65 bits. Initialement, il pesait 176 bits. Par conséquent, nous l'avons réduit jusqu'à 176/65 = 2,7 fois! Mais c'est de l'utopie. Il est peu probable qu'un tel coefficient soit obtenu. Pourquoi? Cela sera discuté un peu plus tard.

Décodage

Eh bien, peut-être la chose la plus simple qui reste est le décodage. Je pense que beaucoup d’entre vous ont deviné qu’il est impossible de créer simplement un fichier compressé sans aucune indication sur la façon dont il a été encodé - nous ne pourrons pas le décoder! Oui, c'était difficile pour moi de réaliser cela, mais j'ai dû créer un fichier texte table.txt avec une table de compression:

 01110 00 A010 E1111 I110 S10 T0110 U01111 Y1110 

Enregistrez le tableau sous la forme de "caractère" "code de caractère". Pourquoi 01110 est-il sans personnage? En fait, c'est avec un symbole, juste les outils java que j'utilise lors de la sortie dans un fichier, le caractère de retour à la ligne - '\ n' - est converti en un retour à la ligne (aussi stupide que cela puisse paraître). Par conséquent, la ligne vide ci-dessus est le caractère pour le code 01110. Pour le code 00, le caractère est un espace au début de la ligne. Je dois dire tout de suite que notre méthode de stockage de cette table peut prétendre la plus irrationnelle. Mais c'est simple à comprendre et à mettre en œuvre. Je serai heureux d'entendre vos recommandations dans les commentaires concernant l'optimisation.

Il est très facile de décoder cette table. Rappelez-vous quelle règle nous a guidés lors de la création de l'encodage:

Aucun code ne doit préfixer un autre

C'est là qu'il joue un rôle de facilitateur. Nous lisons séquentiellement bit par bit et, dès que la chaîne reçue d, constituée de bits lus, correspond au codage correspondant au caractère caractère, nous savons immédiatement que le caractère caractère a été codé (et seulement lui!). Ensuite, nous écrivons des caractères dans la ligne de décodage (la ligne contenant le message décodé), mettons à zéro la ligne d, puis lisons le fichier codé.

Implémentation

Il est temps d' humilier mon code en écrivant un archiveur. Appelons cela Compressor.

Commençons par le début. Tout d'abord, nous écrivons la classe Node:

 public class Node { private int frequence;// private char letter;// private Node leftChild;//  private Node rightChild;//  public Node(char letter, int frequence) { //,  this.letter = letter; this.frequence = frequence; } public Node() {}//    (.       ) public void addChild(Node newNode) {//  if (leftChild == null)//  =>  =>    leftChild = newNode; else { if (leftChild.getFrequence() <= newNode.getFrequence()) // ,   rightChild = newNode;// ,     else { rightChild = leftChild; leftChild = newNode; } } frequence += newNode.getFrequence();//  } public Node getLeftChild() { return leftChild; } public Node getRightChild() { return rightChild; } public int getFrequence() { return frequence; } public char getLetter() { return letter; } public boolean isLeaf() {//   return leftChild == null && rightChild == null; } } 

Maintenant, l'arbre:

 class BinaryTree { private Node root; public BinaryTree() { root = new Node(); } public BinaryTree(Node root) { this.root = root; } public int getFrequence() { return root.getFrequence(); } public Node getRoot() { return root; } } 

File d'attente prioritaire:

 import java.util.ArrayList;//-,      class PriorityQueue { private ArrayList<BinaryTree> data;//  private int nElems;//-    public PriorityQueue() { data = new ArrayList<BinaryTree>(); nElems = 0; } public void insert(BinaryTree newTree) {// if (nElems == 0) data.add(newTree); else { for (int i = 0; i < nElems; i++) { if (data.get(i).getFrequence() > newTree.getFrequence()) {//     data.add(i, newTree);// . ,  c       1  break;//       } if (i == nElems - 1) data.add(newTree); } } nElems++;// -   1 } public BinaryTree remove() {//   BinaryTree tmp = data.get(0);//   data.remove(0);//,  nElems--;// -   1 return tmp;//  (   ) } } 

La classe qui crée l'arbre Huffman:

 public class HuffmanTree { private final byte ENCODING_TABLE_SIZE = 127;//   private String myString;// private BinaryTree huffmanTree;//  private int[] freqArray;//  private String[] encodingArray;//  //----------------constructor---------------------- public HuffmanTree(String newString) { myString = newString; freqArray = new int[ENCODING_TABLE_SIZE]; fillFrequenceArray(); huffmanTree = getHuffmanTree(); encodingArray = new String[ENCODING_TABLE_SIZE]; fillEncodingArray(huffmanTree.getRoot(), "", ""); } //--------------------frequence array------------------------ private void fillFrequenceArray() { for (int i = 0; i < myString.length(); i++) { freqArray[(int)myString.charAt(i)]++; } } public int[] getFrequenceArray() { return freqArray; } //------------------------huffman tree creation------------------ private BinaryTree getHuffmanTree() { PriorityQueue pq = new PriorityQueue(); //   for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { if (freqArray[i] != 0) {//     Node newNode = new Node((char) i, freqArray[i]);//    Node BinaryTree newTree = new BinaryTree(newNode);//  Node  BinaryTree pq.insert(newTree);//   } } while (true) { BinaryTree tree1 = pq.remove();//    . try { BinaryTree tree2 = pq.remove();//     Node newNode = new Node();//  Node newNode.addChild(tree1.getRoot());//      newNode.addChild(tree2.getRoot()); pq.insert(new BinaryTree(newNode); } catch (IndexOutOfBoundsException e) {//     return tree1; } } } public BinaryTree getTree() { return huffmanTree; } //-------------------encoding array------------------ void fillEncodingArray(Node node, String codeBefore, String direction) {//   if (node.isLeaf()) { encodingArray[(int)node.getLetter()] = codeBefore + direction; } else { fillEncodingArray(node.getLeftChild(), codeBefore + direction, "0"); fillEncodingArray(node.getRightChild(), codeBefore + direction, "1"); } } String[] getEncodingArray() { return encodingArray; } public void displayEncodingArray() {//  fillEncodingArray(huffmanTree.getRoot(), "", ""); System.out.println("======================Encoding table===================="); for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { if (freqArray[i] != 0) { System.out.print((char)i + " "); System.out.println(encodingArray[i]); } } System.out.println("========================================================"); } //----------------------------------------------------- String getOriginalString() { return myString; } } 

Classe contenant qui encode / décode:

 public class HuffmanOperator { private final byte ENCODING_TABLE_SIZE = 127;//  private HuffmanTree mainHuffmanTree;//  (   ) private String myString;//  private int[] freqArray;//  private String[] encodingArray;//  private double ratio;//  public HuffmanOperator(HuffmanTree MainHuffmanTree) {//for compress this.mainHuffmanTree = MainHuffmanTree; myString = mainHuffmanTree.getOriginalString(); encodingArray = mainHuffmanTree.getEncodingArray(); freqArray = mainHuffmanTree.getFrequenceArray(); } public HuffmanOperator() {}//for extract; //---------------------------------------compression----------------------------------------------------------- private String getCompressedString() { String compressed = ""; String intermidiate = "";// (  ) //System.out.println("=============================Compression======================="); //displayEncodingArray(); for (int i = 0; i < myString.length(); i++) { intermidiate += encodingArray[myString.charAt(i)]; } //      .       8=> //    ( 1,  ) byte counter = 0;//     (   : 0<=counter<8<127) for (int length = intermidiate.length(), delta = 8 - length % 8; counter < delta ; counter++) {//delta -    intermidiate += "0"; } // -         compressed = String.format("%8s", Integer.toBinaryString(counter & 0xff)).replace(" ", "0") + intermidiate; //  setCompressionRatio(); //System.out.println("==============================================================="); return compressed; } private void setCompressionRatio() {//   double sumA = 0, sumB = 0;//A-the original sum for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { if (freqArray[i] != 0) { sumA += 8 * freqArray[i]; sumB += encodingArray[i].length() * freqArray[i]; } } ratio = sumA / sumB; } public byte[] getBytedMsg() {//final compression StringBuilder compressedString = new StringBuilder(getCompressedString()); byte[] compressedBytes = new byte[compressedString.length() / 8]; for (int i = 0; i < compressedBytes.length; i++) { compressedBytes[i] = (byte) Integer.parseInt(compressedString.substring(i * 8, (i + 1) * 8), 2); } return compressedBytes; } //---------------------------------------end of compression---------------------------------------------------------------- //------------------------------------------------------------extract----------------------------------------------------- public String extract(String compressed, String[] newEncodingArray) { String decompressed = ""; String current = ""; String delta = ""; encodingArray = newEncodingArray; //displayEncodingArray(); // -   for (int i = 0; i < 8; i++) delta += compressed.charAt(i); int ADDED_ZEROES = Integer.parseInt(delta, 2); for (int i = 8, l = compressed.length() - ADDED_ZEROES; i < l; i++) { //i = 8, ..      -   current += compressed.charAt(i); for (int j = 0; j < ENCODING_TABLE_SIZE; j++) { if (current.equals(encodingArray[j])) {//  decompressed += (char)j;//   current = "";//    } } } return decompressed; } public String getEncodingTable() { String enc = ""; for (int i = 0; i < encodingArray.length; i++) { if (freqArray[i] != 0) enc += (char)i + encodingArray[i] + '\n'; } return enc; } public double getCompressionRatio() { return ratio; } public void displayEncodingArray() {//  System.out.println("======================Encoding table===================="); for (int i = 0; i < ENCODING_TABLE_SIZE; i++) { //if (freqArray[i] != 0) { System.out.print((char)i + " "); System.out.println(encodingArray[i]); //} } System.out.println("========================================================"); } } 

Classe qui facilite l'écriture dans un fichier:

 import java.io.File; import java.io.PrintWriter; import java.io.FileNotFoundException; import java.io.FileOutputStream; import java.io.IOException; import java.io.Closeable; public class FileOutputHelper implements Closeable { private File outputFile; private FileOutputStream fileOutputStream; public FileOutputHelper(File file) throws FileNotFoundException { outputFile = file; fileOutputStream = new FileOutputStream(outputFile); } public void writeByte(byte msg) throws IOException { fileOutputStream.write(msg); } public void writeBytes(byte[] msg) throws IOException { fileOutputStream.write(msg); } public void writeString(String msg) { try (PrintWriter pw = new PrintWriter(outputFile)) { pw.write(msg); } catch (FileNotFoundException e) { System.out.println(" ,     !"); } } @Override public void close() throws IOException { fileOutputStream.close(); } public void finalize() throws IOException { close(); } } 

Classe qui facilite la lecture d'un fichier:

 import java.io.FileInputStream; import java.io.EOFException; import java.io.BufferedReader; import java.io.InputStreamReader; import java.io.Closeable; import java.io.File; import java.io.IOException; public class FileInputHelper implements Closeable { private FileInputStream fileInputStream; private BufferedReader fileBufferedReader; public FileInputHelper(File file) throws IOException { fileInputStream = new FileInputStream(file); fileBufferedReader = new BufferedReader(new InputStreamReader(fileInputStream)); } public byte readByte() throws IOException { int cur = fileInputStream.read(); if (cur == -1)//   throw new EOFException(); return (byte)cur; } public String readLine() throws IOException { return fileBufferedReader.readLine(); } @Override public void close() throws IOException{ fileInputStream.close(); } } 

Eh bien, et la classe principale:

 import java.io.File; import java.nio.charset.MalformedInputException; import java.io.FileNotFoundException; import java.io.IOException; import java.nio.file.Files; import java.nio.file.NoSuchFileException; import java.nio.file.Paths; import java.util.List; import java.io.EOFException; public class Main { private static final byte ENCODING_TABLE_SIZE = 127; public static void main(String[] args) throws IOException { try {//       if (args[0].equals("--compress") || args[0].equals("-c")) compress(args[1]); else if ((args[0].equals("--extract") || args[0].equals("-x")) && (args[2].equals("--table") || args[2].equals("-t"))) { extract(args[1], args[3]); } else throw new IllegalArgumentException(); } catch (ArrayIndexOutOfBoundsException | IllegalArgumentException e) { System.out.println("    "); System.out.println(" Readme.txt"); e.printStackTrace(); } } public static void compress(String stringPath) throws IOException { List<String> stringList; File inputFile = new File(stringPath); String s = ""; File compressedFile, table; try { stringList = Files.readAllLines(Paths.get(inputFile.getAbsolutePath())); } catch (NoSuchFileException e) { System.out.println(" ,     !"); return; } catch (MalformedInputException e) { System.out.println("    "); return; } for (String item : stringList) { s += item; s += '\n'; } HuffmanOperator operator = new HuffmanOperator(new HuffmanTree(s)); compressedFile = new File(inputFile.getAbsolutePath() + ".cpr"); compressedFile.createNewFile(); try (FileOutputHelper fo = new FileOutputHelper(compressedFile)) { fo.writeBytes(operator.getBytedMsg()); } //create file with encoding table: table = new File(inputFile.getAbsolutePath() + ".table.txt"); table.createNewFile(); try (FileOutputHelper fo = new FileOutputHelper(table)) { fo.writeString(operator.getEncodingTable()); } System.out.println("   : " + compressedFile.getAbsolutePath()); System.out.println("    " + table.getAbsolutePath()); System.out.println("     !"); double idealRatio = Math.round(operator.getCompressionRatio() * 100) / (double) 100;//  double realRatio = Math.round((double) inputFile.length() / ((double) compressedFile.length() + (double) table.length()) * 100) / (double)100;//  System.out.println("    " + idealRatio); System.out.println("      " + realRatio); } public static void extract(String filePath, String tablePath) throws FileNotFoundException, IOException { HuffmanOperator operator = new HuffmanOperator(); File compressedFile = new File(filePath), tableFile = new File(tablePath), extractedFile = new File(filePath + ".xtr"); String compressed = ""; String[] encodingArray = new String[ENCODING_TABLE_SIZE]; //read compressed file //!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!check here: try (FileInputHelper fi = new FileInputHelper(compressedFile)) { byte b; while (true) { b = fi.readByte();//method returns EOFException compressed += String.format("%8s", Integer.toBinaryString(b & 0xff)).replace(" ", "0"); } } catch (EOFException e) { } //-------------------- //read encoding table: try (FileInputHelper fi = new FileInputHelper(tableFile)) { fi.readLine();//skip first empty string encodingArray[(byte)'\n'] = fi.readLine();//read code for '\n' while (true) { String s = fi.readLine(); if (s == null) throw new EOFException(); encodingArray[(byte)s.charAt(0)] = s.substring(1, s.length()); } } catch (EOFException ignore) {} extractedFile.createNewFile(); //extract: try (FileOutputHelper fo = new FileOutputHelper(extractedFile)) { fo.writeString(operator.extract(compressed, encodingArray)); } System.out.println("    " + extractedFile.getAbsolutePath()); } } 

Le fichier d'instructions readme.txt est à vous de vous écrire :-)

Conclusion

C'est probablement tout ce que je voulais dire. Si vous avez quelque chose à dire sur mon incapacité à améliorer le code, l'algorithme et toute optimisation en général, n'hésitez pas à écrire. Si j'ai mal compris quelque chose, écrivez aussi. Je serai heureux de vous entendre dans les commentaires!

PS

Oui, oui, je suis toujours là, car je n'ai pas oublié le coefficient. Pour la chaîne s1, la table de codage pèse 48 octets - beaucoup plus que le fichier d'origine, et ils n'ont pas oublié les zéros supplémentaires (le nombre de zéros ajoutés est 7) ​​=> le taux de compression sera inférieur à un: 176 / (65 + 48 * 8 + 7) = 0,38. Si vous avez également remarqué cela, alors tout simplement pas en face, vous êtes bien fait. Oui, cette implémentation sera extrêmement inefficace pour les petits fichiers. Mais qu'advient-il des gros fichiers? La taille des fichiers dépasse de loin la taille de la table de codage. Ici, l'algorithme fonctionne comme il se doit! Par exemple, pour le monologue Faust, l' archiveur donne un coefficient réel (non idéalisé) égal à 1,46 - presque une fois et demie! Et oui, le dossier était censé être en anglais.