
Bonjour.
Dans la pratique, vous rencontrez souvent des tâches qui sont loin d'être des algorithmes ML complexes, mais en même temps non moins importantes et urgentes pour l'entreprise.
Parlons de l'un d'eux.
La tâche se résume à distribuer (sciage, rasplitovat - le jargon de l'entreprise est inépuisable) les données d'une table cible avec des agrégats (valeurs agrégées) sur une table de granularité plus détaillée.
Par exemple, le service commercial doit décomposer le plan annuel convenu au niveau de la marque - en détail pour les produits, pour que les spécialistes du marketing décomposent le budget marketing annuel par pays, le service de planification et économique pour décomposer les dépenses commerciales générales par centres de responsabilité financière, etc. etc.
Si vous sentez que des tâches comme celle-ci se profilent déjà devant vous à l'horizon ou traitent déjà ceux qui ont souffert de telles tâches, alors je demande un chat.
Prenons un exemple réel:
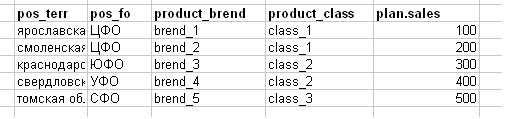
Ils abaissent le plan de vente comme une tâche comme dans l'image ci-dessous (j'ai intentionnellement simplifié l'exemple, en réalité - une bannière Excel de 100-200 Mo).
Explication de la rubrique:
- pos_terr-territoire (région) du débouché
- pos_fo - le district fédéral du point de vente (par exemple, le district fédéral central et le district fédéral central)
- product_brend - marque de produit
- product_class - classe de produit
- plan.sales est un plan de vente pour tout.
Et ils demandent, par exemple, de casser leur méga-table (dans le cadre de l'exemple de nos enfants, c'est bien sûr plus modeste) - au canal de vente. A la question - selon quelle logique se décomposer, j'obtiens la réponse: «mais prenez les statistiques des ventes réelles pour le 4ème trimestre de telle ou telle année, obtenez les parts réelles des canaux en% pour chaque ligne du plan et décomposez ces parties de la ligne du plan».
En fait, c'est la réponse la plus fréquente dans de telles tâches ...
Jusqu'à présent, tout semble assez simple.
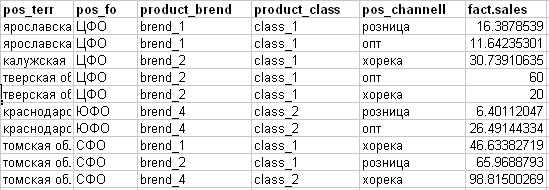
Je comprends ce fait (voir l'image ci-dessous):
- pos_channell - canal de vente (attribut cible pour le plan)
- fact.sales - ventes réelles de quelque chose.
Sur la base de l'approche obtenue du "sciage" sur l'exemple de la première ligne du plan, nous le décomposerons sur la base du fait quelque chose comme ceci:

Cependant, si nous comparons le fait avec le plan pour la plaque entière afin de comprendre si toutes les lignes du plan peuvent être correctement «coupées» en parts, nous obtenons l'image suivante: (vert - tous les attributs de la ligne du plan coïncident avec le fait, les cellules jaunes ne correspondent pas).
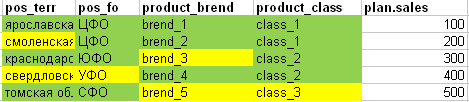
- Dans la 1ère ligne du plan, tous les champs se trouvent complètement dans le fait.
- Dans la 2ème ligne du plan, le territoire correspondant n'a pas été trouvé dans le fait
- La 3ème ligne du plan ne suffit pas dans le fait de la marque
- La 4ème ligne du plan ne suffit pas dans le fait du territoire et du district fédéral
- La 5ème ligne du plan manque en fait de marque et de classe.
Comme l'a dit Panikovsky: "J'ai vu la Shura, vu - ils sont en or ..."

Je vais chez le client professionnel et clarifie sur l'exemple de la 2ème ligne, quel type d'approche voit-il pour de telles situations?
J'obtiens la réponse: «pour les cas où il n'est pas possible de calculer la part des canaux pour la marque n ° 2 dans la région de Smolensk (en tenant compte du fait que nous avons la région de Smolensk dans le district fédéral central-district fédéral central) - alors rompez cette ligne en fonction de la structure des canaux dans l'ensemble du district fédéral central!»
Autrement dit, pour {Smolensk region + brand_2}, nous agrégons le fait au niveau du district fédéral central et divisons la région de Smolensk quelque chose comme ceci:

En remontant et en digérant ce que j'ai entendu, j'essaie de généraliser à une heuristique plus universelle:
S'il n'y a pas de données au niveau de détail actuel de la table de faits, puis avant de calculer les parts pour le champ cible (canal de vente), nous agrégons la table de faits jusqu'à l'attribut de hiérarchie ci-dessus.
Autrement dit, si ce n'est pour le territoire, nous agrégons le fait à un niveau de hiérarchie plus élevé - parts pour le même district fédéral central que dans le plan. Si ce n'est pas pour la marque, alors dans la hiérarchie ci-dessus, il y a une classe de produits - en conséquence, nous recomptons les actions pour la même classe et ainsi de suite.
C'est-à-dire on combine le plan et le fait sur les champs de couplage dont on considère les parts dans le fait et à chaque itération selon le plan non distribué restant, on réduit successivement la composition des champs de couplage.
Un certain modèle de distribution de données se profile déjà ici:
- Nous distribuons en fait le plan basé sur la coïncidence complète des champs correspondants
- Nous obtenons un plan cassé (nous l'accumulons dans le résultat intermédiaire) et un plan ininterrompu (toutes les lignes ne correspondent pas)
- Nous prenons un plan ininterrompu et le divisons en fait à un niveau de hiérarchie supérieur (c'est-à-dire que nous abandonnons un certain champ de couplage de ces 2 tables et agrégons le fait sans ce champ pour calculer les parts)
- Nous obtenons un plan cassé (nous l'ajoutons au résultat intermédiaire) et un plan ininterrompu (toutes les lignes ne correspondent pas)
- Et nous répétons les mêmes étapes jusqu'à ce qu'il n'y ait pas de plan «non résolu».
En général, personne ne nous oblige à supprimer systématiquement les champs d'attelage uniquement dans la hiérarchie. Par exemple, nous avons déjà supprimé la marque et le territoire des champs d'attelage et distribué le plan restant par: product_class (hiérarchie au-dessus de la marque) + Fed.krug (hiérarchie au-dessus du territoire). Et encore obtenu un certain solde non alloué du plan.
En outre, nous pouvons supprimer des champs de couplage soit la classe de produits, soit le district fédéral, comme ils ne sont plus intégrés dans la hiérarchie de l'autre.
Étant donné qu'il y a des dizaines et des rangées de champs dans de telles tables - jusqu'à un million faisant de telles manipulations avec vos mains - la tâche n'est pas la plus agréable.
Et étant donné que des tâches de ce genre me viennent régulièrement à la fin de chaque année (approuver les budgets de l'année suivante au conseil d'administration), vous avez dû traduire ce processus en une sorte de modèle universel flexible.
Et comme la plupart du temps, je travaille avec des données via R - l'implémentation est donc la même.
Tout d'abord, nous devons écrire une fonction magique universelle qui prendra une table de base (basetab) avec des données pour une ventilation (dans notre exemple, un plan) et une table de calcul des parts (sharetab) sur la base desquelles nous "verrons" les données (dans notre exemple, fait). Mais la fonction doit également comprendre ce qui doit être fait avec ces objets, donc la fonction acceptera également le vecteur des noms des champs de couplage (merge.vrs) - c'est-à-dire ces champs qui sont nommés de manière identique dans les deux tables et nous permettront de connecter une table avec les autres champs où elle fonctionne (c'est-à-dire la jointure droite). En outre, la fonction doit comprendre quelle colonne de la table de base doit être prise dans la distribution (basetab.value) et en fonction du champ pour compter les partages (sharetab.value). Eh bien, et le plus important - ce qu'il faut prendre pour le champ résultant (sharetab.targetvars), dans notre cas, nous voulons détailler le plan via le canal de vente.
Par ailleurs, cette variable sharetab.targetvars n'est pas aléatoire au pluriel - il peut ne pas s'agir d'un champ mais d'un vecteur de noms de champ, dans les cas où vous devez ajouter non pas un champ à la table de base de la table de partage mais plusieurs à la fois (par exemple, en fonction du fait, vous ne pouvez pas diviser le plan uniquement par le canal de vente mais aussi par le nom des produits inclus dans la marque).
Oui, et encore une condition :) ma fonction doit être aussi localiste et lisible que possible, sans bâtiment à plusieurs étages sur 2 écrans (je n'aime vraiment pas les grandes fonctions).
Dans la dernière condition, le package dplyr populaire s'intègre aussi confortablement que possible et compte tenu du fait que ses opérateurs de pipeline doivent comprendre les noms textuels des champs qui ont été abaissés dans la fonction, il ne peut pas se passer de l'
évaluation Standart .
Voici ce bébé (sans compter les commentaires internes):
fn_distr <- function(sharetab, sharetab.value, sharetab.targetvars, basetab, basetab.value, merge.vrs,level.txt=NA) { # sharetab - = # sharetab.value - - # sharetab.targetvars - - # basetab - = # basetab.value - # merge.vrs - 2- # level.txt - . ( merge.vrs) require(dplyr) sharetab.value <- as.name(sharetab.value) basetab.value <- as.name(basetab.value) if(is.na(level.txt )){level.txt <- paste0(merge.vrs,collapse = ",")} result <- sharetab %>% group_by(.dots = c(merge.vrs, sharetab.targetvars)) %>% summarise(sharetab.sum = sum(!!sharetab.value)) %>% ungroup %>% group_by(.dots = merge.vrs) %>% mutate(sharetab.share = sharetab.sum / sum(sharetab.sum)) %>% ungroup %>% right_join(y = basetab, by = merge.vrs) %>% mutate(distributed.result = !!basetab.value * sharetab.share, level = level.txt) %>% select(-sharetab.sum,-sharetab.share) return(result) }
En sortie, la fonction doit renvoyer data.frame de l'union de deux tables avec les lignes du plan + fait où il était possible de diviser le plan sur la version actuelle des champs de couplage, et avec les lignes d'origine du plan (et le fait vide) dans les lignes où le plan n'a pas pu être divisé dans l'itération en cours.
Autrement dit, le résultat renvoyé par la fonction après la première itération (briser la première ligne du plan pour la région de Yaroslavl) ressemblera à ceci:
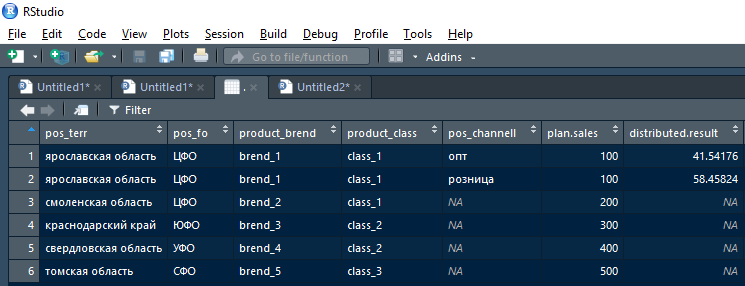
De plus, ce résultat peut être pris par un résultat distribué non vide dans le résultat cumulatif et par un résultat distribué (NA) vide - envoyé à l'itération typique suivante, mais ventilé par part à un niveau hiérarchique supérieur.
Tout le charme et toute la commodité est que le travail est effectué dans le même type de blocs et une fonction universelle, tout ce qui est nécessaire à chaque étape (itération) est de corriger le vecteur merge.vrs et d'observer comment la magie fait tout ce travail fastidieux pour vous:

Oui, j'ai presque oublié une petite nuance: si quelque chose se passe mal et à la fin, nous obtenons un plan cassé qui au total ne sera pas égal au plan avant la panne, il sera difficile de suivre à quelle itération tout s'est mal passé.
Par conséquent, nous fournissons à chaque itération une somme de contrôle:
(_)-(___ )-(___.)=0
Essayons maintenant d'exécuter notre exemple dans le modèle de distribution et de voir ce que nous obtenons à la sortie.
Tout d'abord, récupérez les données source:
library(dplyr) plan <- data_frame(pos_terr = c(" ", " ", " ", " ", " "), pos_fo = c("", "", "", "", ""), product_brend = c("brend_1", "brend_2", "brend_3", "brend_4", "brend_5"), product_class = c("class_1", "class_1", "class_2", "class_2", "class_3"), plan.sales = c(100, 200, 300, 400, 500)) fact <- data_frame(pos_terr = c(" ", " ", " ", " ", " "," ", " ", " ", " ", " "), pos_fo = c("", "","","", "", "", "", "", "", ""), product_brend = c("brend_1", "brend_1", "brend_2", "brend_2","brend_2", "brend_4", "brend_4", "brend_1", "brend_2", "brend_4"), product_class = c("class_1", "class_1", "class_1","class_1","class_1", "class_2", "class_2", "class_1", "class_1", "class_2"), pos_channell = c("", "", "","", "", "", "", "", "", ""), fact.sales = c(16.38, 11.64, 30.73,60, 20, 6.40, 26.49, 46.63, 65.96, 98.81)) </soure> ( ) . <source> plan.remain <- plan result.total <- data_frame()
1. Nous distribuons par Terr, FD (district fédéral), marque, classe merge.fields <- c("pos_terr","pos_fo","product_brend", "product_class") result.current <- fn_distr(sharetab = fact,sharetab.value = "fact.sales",sharetab.targetvars = "pos_channell", basetab = plan.remain,basetab.value = "plan.sales",merge.vrs = merge.fields) result.total <- result.current %>% filter(!is.na(distributed.result)) %>% select(-plan.sales) %>% bind_rows(result.total) # - plan.remain <- result.current %>% filter(is.na(distributed.result)) %>% select(colnames(plan)) # = cat(" :",sum(plan.remain$plan.sales)+sum(result.total$distributed.result)-sum(plan$plan.sales),"\n", " :",nrow(plan.remain)," ")
 2. Nous distribuons par pho, marque, classe (c'est-à-dire que nous abandonnons le territoire en fait)
2. Nous distribuons par pho, marque, classe (c'est-à-dire que nous abandonnons le territoire en fait)La seule différence avec le premier bloc est qu'ils ont légèrement raccourci merge.fields en supprimant pos_terr dedans
merge.fields <- c("pos_fo","product_brend", "product_class") result.current <- fn_distr(sharetab = fact,sharetab.value = "fact.sales",sharetab.targetvars = "pos_channell", basetab = plan.remain,basetab.value = "plan.sales",merge.vrs = merge.fields) result.total <- result.current %>% filter(!is.na(distributed.result)) %>% select(-plan.sales) %>% bind_rows(result.total) plan.remain <- result.current %>% filter(is.na(distributed.result)) %>% select(colnames(plan)) cat(" :",sum(plan.remain$plan.sales)+sum(result.total$distributed.result)-sum(plan$plan.sales),"\n", " :",nrow(plan.remain)," ")
3. Distribuer par pho, classe merge.fields <- c("pos_fo", "product_class") result.current <- fn_distr(sharetab = fact,sharetab.value = "fact.sales",sharetab.targetvars = "pos_channell", basetab = plan.remain,basetab.value = "plan.sales",merge.vrs = merge.fields) result.total <- result.current %>% filter(!is.na(distributed.result)) %>% select(-plan.sales) %>% bind_rows(result.total) plan.remain <- result.current %>% filter(is.na(distributed.result)) %>% select(colnames(plan)) cat(" :",sum(plan.remain$plan.sales)+sum(result.total$distributed.result)-sum(plan$plan.sales),"\n", " :",nrow(plan.remain)," ")
4. Distribuer par classe merge.fields <- c( "product_class") result.current <- fn_distr(sharetab = fact,sharetab.value = "fact.sales",sharetab.targetvars = "pos_channell", basetab = plan.remain,basetab.value = "plan.sales",merge.vrs = merge.fields) result.total <- result.current %>% filter(!is.na(distributed.result)) %>% select(-plan.sales) %>% bind_rows(result.total) plan.remain <- result.current %>% filter(is.na(distributed.result)) %>% select(colnames(plan)) cat(" :",sum(plan.remain$plan.sales)+sum(result.total$distributed.result)-sum(plan$plan.sales),"\n", " :",nrow(plan.remain)," ")
 5. Distribuer par FD
5. Distribuer par FD merge.fields <- c( "pos_fo") result.current <- fn_distr(sharetab = fact,sharetab.value = "fact.sales",sharetab.targetvars = "pos_channell", basetab = plan.remain,basetab.value = "plan.sales",merge.vrs = merge.fields) result.total <- result.current %>% filter(!is.na(distributed.result)) %>% select(-plan.sales) %>% bind_rows(result.total) plan.remain <- result.current %>% filter(is.na(distributed.result)) %>% select(colnames(plan)) cat(" :",sum(plan.remain$plan.sales)+sum(result.total$distributed.result)-sum(plan$plan.sales),"\n", " :",nrow(plan.remain)," ")
Comme vous pouvez le voir, il n'y a plus de plan «non scié» et l'arithmétique du plan distribué est égale à celle d'origine.

Et voici le résultat avec les canaux de vente (dans la colonne de droite, la fonction affiche les champs pour lesquels le couplage / agrégation était destiné, afin que nous puissions plus tard comprendre d'où venait cette distribution):

C'est tout. L'article n'était pas très petit, mais il y a plus de texte explicatif que le code lui-même.
J'espère que cette approche flexible me fera gagner du temps et des nerfs non seulement :-)
Merci de votre attention.