Écrire XGBoost à partir de zéro - partie 1: arbres de décision

Bonjour, Habr!

Après de nombreuses recherches de guides de haute qualité sur les arbres de décision et les algorithmes d'ensemble (boosting, décision forestière, etc.) avec leur implémentation directe dans les langages de programmation, et sans rien trouver (celui qui trouve - écrivez dans les commentaires, j'apprendrai peut-être quelque chose de nouveau), J'ai décidé de faire ma propre direction, comme j'aimerais le voir. La tâche en mots est simple, mais, comme vous le savez, le diable est dans les petites choses, dont il existe de nombreux algorithmes avec des arbres.

Étant donné que le sujet est assez vaste, il sera très difficile de tout mettre en un seul article, il y aura donc deux publications: la première est consacrée aux arbres et la deuxième partie sera consacrée à la mise en œuvre de l'algorithme de renforcement du gradient. Tout le matériel présenté ici est compilé et conçu sur la base de sources ouvertes, mon code, le code de mes collègues et amis. Je vous préviens tout de suite, il y aura beaucoup de code.



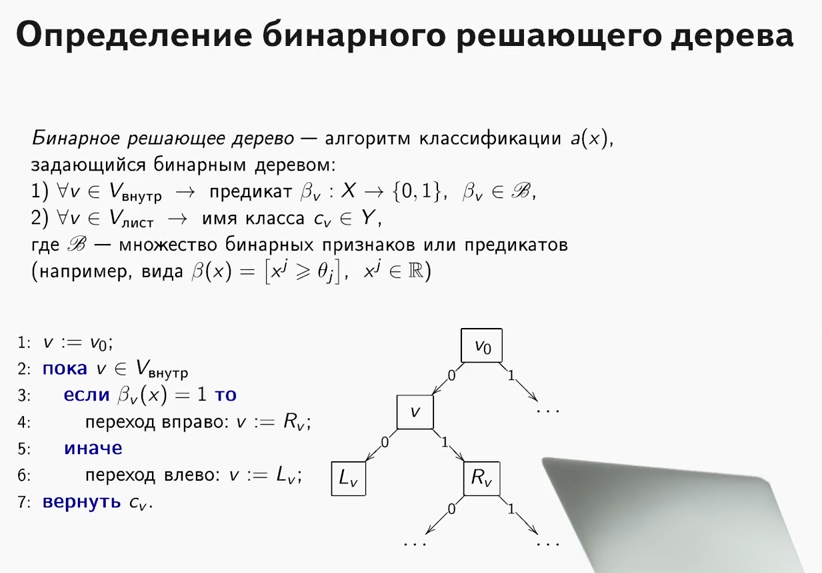
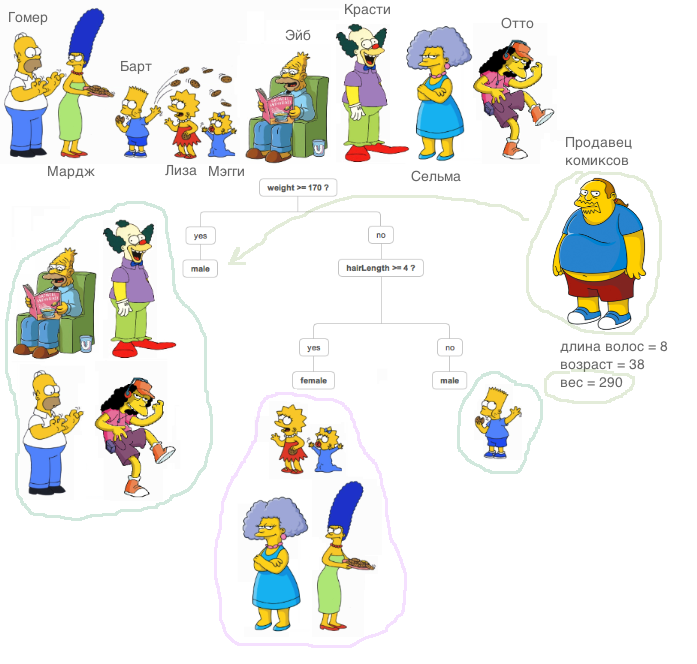
Alors, que devez-vous savoir et être en mesure d'apprendre à écrire vos propres algorithmes d'ensemble avec des arbres de décision à partir de zéro? Puisqu'un ensemble d'algorithmes n'est rien d'autre qu'une composition d '«algorithmes faibles», l'écriture d'un bon ensemble nécessite de bons «algorithmes faibles», nous les analyserons en détail dans cet article. Comme son nom l'indique, ce sont des arbres cruciaux, et en passant du simple au complexe, nous apprendrons à les écrire. Dans ce cas, l'accent sera mis directement sur la mise en œuvre, toute la théorie sera présentée au minimum, je donnerai essentiellement des liens vers des matériaux pour une étude indépendante.

Pour apprendre le matériel, vous devez comprendre à quel point notre algorithme est bon ou mauvais. Nous comprendrons très simplement - nous fixerons certains ensembles de données spécifiques et nous comparerons nos algorithmes avec les algorithmes d'arbres de Sklearn (enfin, ce qui se passerait sans cette bibliothèque). Nous comparerons beaucoup: la complexité de l'algorithme, les métriques sur les données, la disponibilité, etc.

Qu'est-ce qu'un arbre décisif? Un très bon matériel, qui explique le principe de l'arbre de décision, est contenu dans le cours ODS (au fait, un cours sympa, je le recommande à ceux qui commencent leur connaissance du ML).

Une explication très importante: dans tous les cas décrits ci-dessous, tous les signes seront réels, nous ne ferons pas de transformations spéciales avec des données en dehors des algorithmes (nous comparons des algorithmes, pas des jeux de données).

Maintenant, apprenons à résoudre le problème de la régression à l'aide d'arbres de décision. Nous utiliserons la métrique MSE comme entropie.

Nous implémentons une classe RegressionTree très simple, basée sur une approche récursive. Intentionnellement, nous commençons par une implémentation très inefficace mais facile à comprendre d'une telle classe afin de pouvoir l'améliorer à l'avenir.

1. Classe RegressionTree ()

 class RegressionTree(): '''  RegressionTree   .    ,      . ''' def __init__(self, max_depth=3, n_epoch=10, min_size=8): '''   . ''' self.max_depth = max_depth #   self.min_size = min_size #    self.value = 0 #    (   ) self.feature_idx = -1 #    self.feature_threshold = 0 #    self.left = None #   self.right = None #   def fit(self, X, y): '''   .     . ''' #    self.value = y.mean() base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #       prev_error_left = base_error prev_error_right = 0 #     0 -  if self.max_depth <= 1: return dim_shape = X.shape[1] #       left_value = 0 right_value = 0 #     for feat in range(dim_shape): #   idxs = np.argsort(X[:, feat]) #        N = X.shape[0] N1, N2 = N, 0 thres = 1 #      while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #    if thres < N - 1 and x == X[idxs[thres + 1], feat]: thres += 1 continue # ,         target_right = y[idxs][:thres] target_left = y[idxs][thres:] mean_right = y[idxs][:thres].mean(), mean_left = y[idxs][thres:].mean() #        - #   (  ) left_shape = target_left.shape[0] right_shape = target_right.shape[0] mean_left_array = [mean_left for _ in range(left_shape)] mean_right_array = [mean_right for _ in range(right_shape)] #      prev_error_left = N1/N * mse(target_left, mean_left_array) prev_error_right = N2/N * mse(target_right, mean_right_array) #    ,   if (prev_error_left + prev_error_right < error): if (min(N1,N2) > self.min_size): self.feature_idx = feat self.feature_threshold = x left_value = mean_left right_value = mean_right flag = 1 error = prev_error_left + prev_error_right thres += 1 #     ,  if self.feature_idx == -1: return #   -   ,    #   -     self.left = RegressionTree(self.max_depth - 1) self.left.value = left_value self.right = RegressionTree(self.max_depth - 1) self.right.value = right_value #   idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #  self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): '''     -  ,         self.value -    . ''' if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): '''    -      __predict(). ''' y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

Je vais expliquer brièvement ce que fait chaque méthode ici.

La méthode d' fit , comme son nom l'indique, enseigne le modèle. Un échantillon d'apprentissage est appliqué à l'entrée et une procédure d'apprentissage d'arbre a lieu. En triant les signes, nous recherchons la meilleure partition de l'arbre en termes de réduction de l'entropie, en l'occurrence mse . Pour déterminer qu'il était possible de trouver une bonne répartition est très simple, il suffit de remplir deux conditions. Nous ne voulons pas que peu d'objets tombent dans la partition (protection contre le recyclage), et l'erreur moyenne pour mse devrait être inférieure à l'erreur qui est maintenant dans l'arborescence - nous recherchons le même gain en gain d' informations . Après avoir parcouru tous les signes et toutes les valeurs uniques de cette manière, nous allons parcourir toutes les options et choisir la meilleure partition. Et puis nous faisons un appel récursif sur les partitions reçues jusqu'à ce que les conditions de sortie de la récursivité soient remplies.

La méthode __predict , comme son nom l'indique, crée un prédicat. Après avoir reçu un objet en entrée, il passe par les nœuds de l'arborescence résultante - dans chaque nœud, le numéro et la valeur de l'attribut y sont fixés, et selon la valeur que la méthode entrante de l'objet utilise pour cet attribut, nous allons soit vers la droite, soit vers la gauche, jusqu'à ce que nous arrivions à la feuille, dans laquelle il y aura une réponse pour cet objet.

La méthode de predict fait la même chose que la méthode précédente, uniquement pour un groupe d'objets.

Nous importons l'ensemble de données sur la maison bien connu de la Californie. Il s'agit d'un ensemble de données régulier avec des données et une cible pour résoudre le problème de régression.

 data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) 

Eh bien, commençons la comparaison! Voyons d'abord à quelle vitesse l'algorithme apprend. Nous définissons dans Sklearn et nous-mêmes le seul paramètre max_depth , qu'il soit égal à 2.

 %%time A = RegressionTree(2) #    A.fit(X,y) 

 from sklearn.tree import DecisionTreeRegressor %%time model = DecisionTreeRegressor(max_depth=2) #  Sklearn model.fit(X,y) 

Les éléments suivants s'affichent:

• Pour notre algorithme - Temps CPU: utilisateur 4min 47s, sys: 8,25 ms, total: 4min 47s
  Temps de mur: 4min 47s
• Pour Sklearn - Temps CPU: utilisateur 53,5 ms, sys: 0 ns, total: 53,5 ms
  Temps de mur: 53,4 ms

Comme vous pouvez le voir, l'algorithme apprend des milliers de fois plus lentement. Quelle en est la raison? Faisons les choses correctement.

Rappelez-vous comment la procédure de recherche de la meilleure partition est organisée. Comme vous le savez, dans le cas général, avec la taille des objets $$$N$ et avec le nombre de signes $$$d$ , la difficulté de trouver la meilleure répartition est $$$O (N * logN * d)$ .

D'où vient cette complexité?

Tout d'abord, pour recalculer efficacement l'erreur, il est nécessaire de trier toutes les colonnes afin de passer de la plus petite à la plus grande avant de passer par l'attribut. Comme nous le faisons pour chaque trait, cela crée une complexité correspondante. Comme vous pouvez le voir, nous trions les signes, mais le problème réside dans le recalcul de l'erreur - chaque fois que nous introduisons les données dans la méthode mse , qui fonctionne pour la ligne. Cela rend le recomptage des erreurs si inefficace! Après tout, la difficulté de trouver un fractionnement augmente $$$O (N ^ 2 * d)$ pour grand $$$N$ ralentit considérablement l'algorithme. Par conséquent, nous procédons sans problème au point suivant.

2. Classe RegressionTree () avec recomptage rapide des erreurs

Que faut-il faire pour retracer rapidement l'erreur? Prenez un stylo et du papier et peignez comment changer les formules.

Supposons qu'à une certaine étape, il y ait déjà une erreur calculée pour $$$N$ objets. Il a la formule suivante: $$$\ sum_ {i = 1} ^ n (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2$ . Ici, il faut diviser par $$$N$ mais pour l'instant, omettons-le. Nous voulons obtenir rapidement cette erreur - $$$\ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2$ , c'est-à-dire, jette l'erreur que l'élément introduit $$$y_i$ à une autre partie.

Puisque nous lançons l'objet, l'erreur doit être racontée à deux endroits - du côté droit (à l'exclusion de cet objet) et du côté gauche (en tenant compte de cet objet). Mais sans perte de généralité, nous ne déduirons qu'une seule formule, car elles seront similaires.

Comme nous travaillons avec mse , nous n'avons pas eu de chance: il est assez difficile de dériver un recomptage rapide d'une erreur, mais lorsque vous travaillez avec d'autres métriques (par exemple, le critère de Gini, si nous résolvons le problème de classification), le recomptage rapide est beaucoup plus facile.

Eh bien, commençons à dériver des formules!

$$

$$\ sum_ {i = 1} ^ N (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 + (y_N - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2$$

Nous écrirons le premier membre:

$$

$$\ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1 } (y_i - \ frac {\ sum_ {i = 1} ^ {N-1} y_i + y_N} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac { Ny_i - \ sum_ {i = 1} ^ {N-1} y_i} {N} - \ frac {y_N} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N} - \ frac {y_N - y_i} {N}) ^ 2 = \\ \ sum_ {i = 1 } ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) ^ 2 - 2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} + (\ frac {y_N - y_i} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) ^ 2 - \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} - (\ frac {y_N - y_i} {N}) ^ 2) = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2 * (\ frac {N-1} {N}) ^ 2 - \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} - \\ - (\ frac {y_N - y_i} { N}) ^ 2)$$

Ugh, juste un peu à gauche. Il ne reste plus qu'à exprimer le montant requis.

$$

$$\ sum_ {i = 1} ^ {N} (y_i - \ frac {\ sum_ {i = 1} ^ {N} y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1 } (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2 * (\ frac {N-1} {N}) ^ 2 - \\ \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) (\ frac {y_N - y_i} {N}) - (\ frac {y_N - y_i} {N}) ^ 2) + (y_N - \ sum_ {i = 1} ^ {N} \ frac {y_i} {N}) ^ 2$$

Et puis, il est clair comment exprimer le montant souhaité. Pour recalculer l'erreur, nous devons stocker uniquement la somme des éléments à droite et à gauche, ainsi que le nouvel élément lui-même, qui est arrivé à l'entrée. Maintenant l'erreur est racontée pour $$$O (1)$ .

Eh bien, implémentons cela dans le code.

 class RegressionTreeFastMse(): '''  RegressionTree    .        O(1). ''' #    def __init__(self, max_depth=3, min_size=10): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None #   -     def fit(self, X, y): #   -   y self.value = y.mean() #   - mse     (  # ,     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2 ,    -   #   - -    if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 #   ,  if self.feature_idx == -1: return self.left = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.left.value = left_value self.right = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.right.value = right_value idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

Mesurons le temps consacré à la formation et comparons avec l'analogue de Sklearn.

 %%time A = RegressionTreeFastMse(4, min_size=5) A.fit(X,y) test_mytree = A.predict(X) test_mytree 

 %%time model = DecisionTreeRegressor(max_depth=4) model.fit(X,y) test_sklearn = model.predict(X) 

• Pour notre algorithme, nous obtenons - Temps CPU: utilisateur 3,11 s, sys: 2,7 ms, total: 3,11 s
  Temps de mur: 3,11 s.
• Pour l'algorithme de Sklearn - Temps CPU: utilisateur 45,9 ms, sys: 1,09 ms, total: 47 ms
  Temps de mur: 45,7 ms.

Les résultats sont déjà plus agréables. Eh bien, améliorons encore l'algorithme.

3. Classe RegressionTree () avec des combinaisons linéaires d'entités

Maintenant, dans notre algorithme, les relations entre les attributs ne sont en aucun cas utilisées. Nous corrigeons une caractéristique et examinons uniquement les partitions orthogonales de l'espace. Comment apprendre à utiliser les relations linéaires entre les attributs? Autrement dit, rechercher les meilleures partitions n'est pas comme $$$a_ {feat} <x$ et $$$\ sum_ {i = 1} ^ K b_i * a_i <x$ où $$$K$ - est un nombre inférieur à la dimension de notre espace?

Il existe de nombreuses options, je vais en souligner deux des plus intéressantes de mon point de vue. Ces deux approches sont décrites dans le livre de Friedman (il a inventé ces arbres).

Je vais donner une image pour que ce soit clair:



Tout d'abord, vous pouvez essayer de trouver ces partitions linéaires de manière algorithmique. Il est clair qu'il est impossible de trier toutes les combinaisons linéaires, car il existe un nombre infini de combinaisons, un tel algorithme doit donc être gourmand, c'est-à-dire qu'à chaque itération, améliorer le résultat de l'itération précédente. L'idée principale de cet algorithme peut être lue dans le livre, je vais également laisser un lien ici vers le référentiel de mon ami et collègue avec la mise en œuvre de cet algorithme.

Deuxièmement, si nous n'allons pas loin de l'idée de trouver la meilleure partition orthogonale, alors comment modifier le jeu de données afin que les informations sur la relation des entités soient utilisées et que la recherche soit basée sur des partitions orthogonales? C'est vrai, pour faire une sorte de transformation des fonctionnalités originales en de nouvelles. Par exemple, vous pouvez prendre la somme d'une combinaison de fonctionnalités et rechercher déjà des partitions par elles. Une telle méthode s'intègre plus mal dans le concept algorithmique, mais elle remplit sa tâche - elle recherche des partitions orthogonales déjà dans une sorte d'interconnexion d'attributs.

Eh bien, implémentons-le - nous ajouterons de nouvelles fonctionnalités, par exemple, toutes sortes de combinaisons de sommes de fonctionnalités $$$i, j$ où $$$I <j$ . Je note que la complexité de l'algorithme dans ce cas augmentera, il est clair combien de fois. Eh bien, pour être considéré plus rapidement, nous utiliserons le cython.

 %load_ext Cython %%cython -a import itertools import numpy as np cimport numpy as np from itertools import * cdef class RegressionTreeCython: cdef public int max_depth cdef public int feature_idx cdef public int min_size cdef public int averages cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef RegressionTreeCython left cpdef RegressionTreeCython right def __init__(self, max_depth=3, min_size=4, averages=1): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.averages = averages self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None def data_transform(self, np.ndarray[np.float64_t, ndim=2] X, list index_tuples): #   -       for i in index_tuples: #  ,       X = np.hstack((X, X[:, i[0]:(i[1]+1)].sum(axis=1).reshape(X.shape[0],1))) return X def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef np.float64_t mean1 = 0.0 cpdef np.float64_t mean2 = 0.0 cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef np.float64_t delta1 = 0.0 cpdef np.float64_t delta2 = 0.0 cpdef np.float64_t sm1 = 0.0 cpdef np.float64_t sm2 = 0.0 cpdef list index_tuples cpdef list stuff cpdef long idx = 0 cpdef np.float64_t prev_error1 = 0.0 cpdef np.float64_t prev_error2 = 0.0 cpdef long thres = 0 cpdef np.float64_t error = 0.0 cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 #        #  ,     if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(combinations(stuff,2)) #    X = self.data_transform(X, index_tuples) #   -   y self.value = y.mean() #   - mse     (  , #     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2    -   #   -      if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 # self.feature_idx -     . #   -  ,    -   #  ,   ,     #   ,  if self.feature_idx == -1: return #    self.left = RegressionTreeCython(self.max_depth - 1, averages=0) self.left.value = left_value self.right = RegressionTreeCython(self.max_depth - 1, averages=0) self.right.value = right_value #      idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #   self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): #   ,        if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(itertools.combinations(stuff,2)) X = self.data_transform(X, index_tuples) y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

4. Comparaison des résultats

Eh bien, comparons les résultats. Nous comparerons trois algorithmes avec les mêmes paramètres - un arbre de Sklearn, notre arbre ordinaire et notre arbre avec de nouvelles fonctionnalités. Nous diviserons notre ensemble de données en ensembles de formation et de test à plusieurs reprises et calculerons l'erreur.

 from sklearn.model_selection import KFold def get_metrics(X,y,n_folds=2, model=None): kf = KFold(n_splits=n_folds, shuffle=True) kf.get_n_splits(X) er_list = [] for train_index, test_index in kf.split(X): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model.fit(X_train,y_train) predict = model.predict(X_test) er_list.append(mse(y_test, predict)) return er_list 

Maintenant, exécutons tous les algorithmes.

 import matplotlib.pyplot as plt data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_sklearn_tree = get_metrics(X,y,30,DecisionTreeRegressor(max_depth=4, min_samples_leaf=10)) er_fast_mse_tree = get_metrics(X,y,30,RegressionTreeFastMse(4, min_size=10)) er_averages_tree = get_metrics(X,y,30,RegressionTreeCython(4, min_size=10)) %matplotlib inline data = [er_sklearn_tree, er_fast_mse_tree, er_averages_tree] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Tree', 'Fast Mse Tree', 'Averages Tree']) plt.grid() plt.show() 

Résultats:



Notre arbre normal perdu pour Sklearn (ce qui est compréhensible: Sklearn est bien optimisé, et par défaut, il utilise beaucoup de paramètres dans l'arbre que nous ne prenons pas en compte), mais lors de l'ajout de montants, le résultat devient plus agréable.

Pour résumer: nous avons appris à écrire des arbres décisifs à partir de zéro, appris à améliorer leurs performances et testé leur efficacité sur des ensembles de données réels en les comparant avec l'algorithme de Sklearn. Cependant, les méthodes présentées ici ne limitent pas l'amélioration des algorithmes, alors gardez à l'esprit que le code proposé peut être encore amélioré. Dans le prochain article, nous écrirons le boosting basé sur ces algorithmes.

Tout succès!