Écrire XGBoost à partir de zéro - partie 2: renforcement du gradient

Bonjour à tous!

Dans le dernier article, nous avons compris comment les arbres de décision sont organisés, et à partir de zéro, nous avons implémenté
algorithme de construction, optimisant et améliorant simultanément. Dans cet article, nous allons implémenter l'algorithme de renforcement du gradient et à la fin, nous créerons notre propre XGBoost. La narration suivra le même schéma: nous écrivons un algorithme, le décrivons, le résumons en comparant les résultats du travail avec des analogues de Sklearn.

Dans cet article, l'accent sera également mis sur l'implémentation dans le code, il est donc préférable de lire la théorie ensemble dans un autre (par exemple, dans le cours ODS ), et déjà avec une connaissance de la théorie, vous pouvez passer à cet article, car le sujet est assez compliqué.



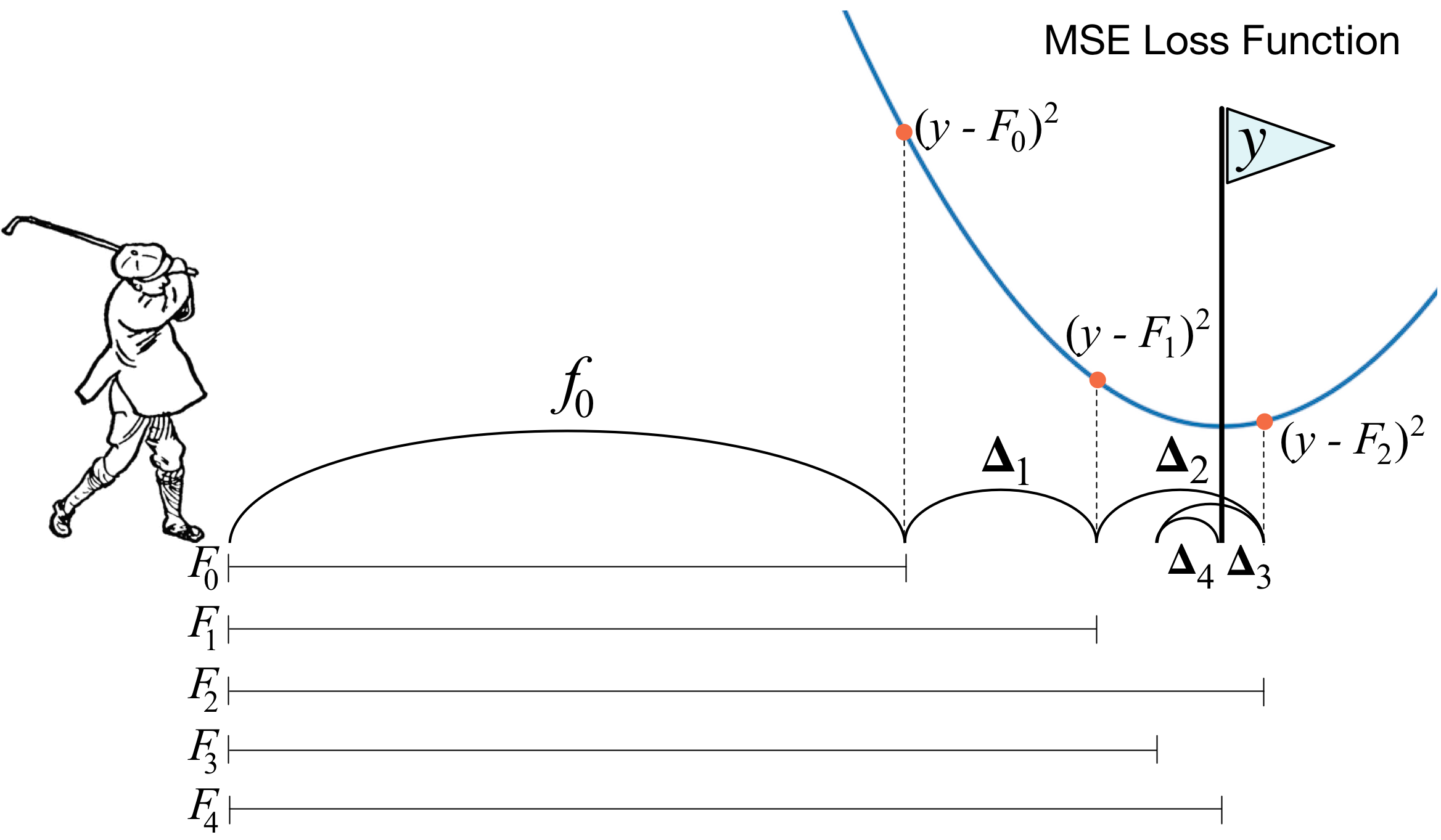
Qu'est-ce que le boost de dégradé? Une photo d'un golfeur décrit parfaitement l'idée principale. Afin de conduire la balle dans le trou, le golfeur effectue chaque coup suivant en tenant compte de l'expérience des coups précédents - pour lui, c'est une condition nécessaire pour mettre la balle dans le trou. Si c'est très grossier (je ne suis pas un maître du golf :)), à chaque nouveau coup, la première chose qu'un golfeur regarde est la distance entre la balle et le trou après le coup précédent. Et la tâche principale est de réduire cette distance au coup suivant.

Le boosting est construit de manière très similaire. Premièrement, nous devons introduire la définition de «trou», c'est-à-dire l'objectif que nous viserons. Deuxièmement, nous devons apprendre à comprendre de quel côté nous devons battre avec un club afin de nous rapprocher de la cible. Troisièmement, en tenant compte de toutes ces règles, vous devez trouver la bonne séquence de coups pour que chaque coup suivant réduise la distance entre la balle et le trou.

Nous donnons maintenant une définition légèrement plus rigoureuse. Nous introduisons le modèle de vote pondéré:

$$

$$h (x) = \ sum_ {i = 1} ^ nb_ia_i, x \ in X, b_i \ in R$$

Ici $$$X$Est-ce l'espace d'où nous prenons des objets, $$$b_i, a_i$- c'est le coefficient devant le modèle et le modèle lui-même, c'est-à-dire l'arbre de décision. Supposons que déjà à un certain stade, en utilisant les règles décrites, il était possible d'ajouter à la composition $$$T-1$algorithme faible. Apprendre à comprendre quel type d'algorithme doit être en cours $$$T$, nous introduisons la fonction d'erreur:

$$$err (h) = \ sum_ {j = 1} ^ N L (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j)) \ rightarrow min_ {a_T, b_T}$

Il s'avère que le meilleur algorithme sera celui qui peut minimiser l'erreur reçue lors des itérations précédentes. Et comme le boosting est en gradient, cette fonction d'erreur doit nécessairement avoir un vecteur antigradient le long duquel vous pouvez vous déplacer à la recherche d'un minimum. C’est tout!

Immédiatement avant la mise en œuvre, j'ajouterai quelques mots sur la façon dont tout sera organisé avec nous. Comme dans l'article précédent, nous considérons MSE comme une perte. Calculons son gradient:

$$

$$mse (y, prédire) = (y - prédire) ^ 2 \\ \ nabla_ {prédire} mse (y, prédire) = prédire - y$$

Ainsi, le vecteur antigradient sera égal à $$$y - prévoir$. Sur la marche $$$i$nous considérons les erreurs de l'algorithme obtenues lors des itérations précédentes. Ensuite, nous formons notre nouvel algorithme sur ces erreurs, puis l'ajoutons à notre ensemble avec un signe moins et un certain coefficient.

Commençons maintenant.

1. Implémentation de la classe de boosting de gradient habituelle

import pandas as pd import matplotlib.pyplot as plt import numpy as np from tqdm import tqdm_notebook from sklearn import datasets from sklearn.metrics import mean_squared_error as mse from sklearn.tree import DecisionTreeRegressor import itertools %matplotlib inline %load_ext Cython %%cython -a import itertools import numpy as np cimport numpy as np from itertools import * cdef class RegressionTreeFastMse: cdef public int max_depth cdef public int feature_idx cdef public int min_size cdef public int averages cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef RegressionTreeFastMse left cpdef RegressionTreeFastMse right def __init__(self, max_depth=3, min_size=4, averages=1): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef np.float64_t mean1 = 0.0 cpdef np.float64_t mean2 = 0.0 cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef np.float64_t delta1 = 0.0 cpdef np.float64_t delta2 = 0.0 cpdef np.float64_t sm1 = 0.0 cpdef np.float64_t sm2 = 0.0 cpdef list index_tuples cpdef list stuff cpdef long idx = 0 cpdef np.float64_t prev_error1 = 0.0 cpdef np.float64_t prev_error2 = 0.0 cpdef long thres = 0 cpdef np.float64_t error = 0.0 cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 #   -   y self.value = y.mean() #   - mse     base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -  ,  ,    delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 #   ,  if self.feature_idx == -1: return #    self.left = RegressionTreeFastMse(self.max_depth - 1) self.left.value = left_value self.right = RegressionTreeFastMse(self.max_depth - 1) self.right.value = right_value #      idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #   self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

 class GradientBoosting(): def __init__(self, n_estimators=100, learning_rate=0.1, max_depth=3, random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'): self.n_estimators = n_estimators self.max_depth = max_depth self.learning_rate = learning_rate self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]]) self.min_size = min_size self.loss_by_iter = [] self.trees_ = [] self.loss_by_iter_test = [] self.n_samples = n_samples self.base_tree = base_tree def fit(self, X, y): self.X = X self.y = y b = self.initialization(y) prediction = b.copy() for t in tqdm_notebook(range(self.n_estimators)): if t == 0: resid = y else: #    resid = (y - prediction) #    if self.base_tree == 'Bagging': tree = Bagging(max_depth=self.max_depth, min_size = self.min_size) if self.base_tree == 'Tree': tree = RegressionTreeFastMse(max_depth=self.max_depth, min_size = self.min_size) #     tree.fit(X, resid) #        b = tree.predict(X).reshape([X.shape[0]]) self.trees_.append(tree) prediction += self.learning_rate * b #       if t > 0: self.loss_by_iter.append(mse(y,prediction)) return self def predict(self, X): #   –          pred = np.ones([X.shape[0]]) * np.mean(self.y) #    for t in range(self.n_estimators): pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]]) return pred 

Nous allons maintenant construire la courbe de perte sur l'ensemble d'apprentissage pour nous assurer qu'à chaque itération, nous avons vraiment une diminution.

 GDB = GradientBoosting(n_estimators=50) GDB.fit(X,y) x = GDB.predict(X) plt.grid() plt.title('Loss by iterations') plt.plot(GDB.loss_by_iter) 

2. Ensachage sur des arbres décisifs

Eh bien, avant de comparer les résultats, parlons de la procédure d' ensachage sur les arbres.

Tout est simple ici: nous voulons nous protéger de la reconversion, et donc, à l'aide de l'échantillonnage avec retour, nous allons faire la moyenne de nos prévisions afin de ne pas tomber accidentellement sur les émissions (pourquoi cela fonctionne - mieux lire le lien).

 class Bagging(): '''  Bagging -      . ''' def __init__(self, max_depth = 3, min_size=10, n_samples = 10): #super(CART, self).__init__() self.max_depth = max_depth self.min_size = min_size self.n_samples = n_samples self.subsample_size = None self.list_of_Carts = [RegressionTreeFastMse(max_depth=self.max_depth, min_size=self.min_size) for _ in range(self.n_samples)] def get_bootstrap_samples(self, data_train, y_train): #      indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size)) samples_train = data_train[indices] samples_y = y_train[indices] return samples_train, samples_y def fit(self, data_train, y_train): #    self.subsample_size = int(data_train.shape[0]) samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train) for i in range(self.n_samples): self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1)) return self def predict(self, test_data): #        num_samples = test_data.shape[0] pred = [] for i in range(self.n_samples): pred.append(self.list_of_Carts[i].predict(test_data)) pred = np.array(pred).T return np.array([np.mean(pred[i]) for i in range(num_samples)]) 

Eh bien, maintenant, en tant qu'algorithme de base, nous pouvons utiliser non pas un arbre, mais l'ensachage d'arbres - encore une fois, nous nous protégerons contre le recyclage.

3. Résultats

Comparez les résultats de nos algorithmes.

 from sklearn.model_selection import KFold import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn import copy def get_metrics(X,y,n_folds=2, model=None): kf = KFold(n_splits=n_folds, shuffle=True) kf.get_n_splits(X) er_list = [] for train_index, test_index in tqdm_notebook(kf.split(X)): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model.fit(X_train,y_train) predict = model.predict(X_test) er_list.append(mse(y_test, predict)) return er_list data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_boosting = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Tree' )) er_boobagg = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Bagging' )) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=40, learning_rate=0.1)) %matplotlib inline data = [er_sklearn_boosting, er_boosting, er_boobagg] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Boosting', 'Boosting', 'BooBag']) plt.grid() plt.show() 

Reçu:



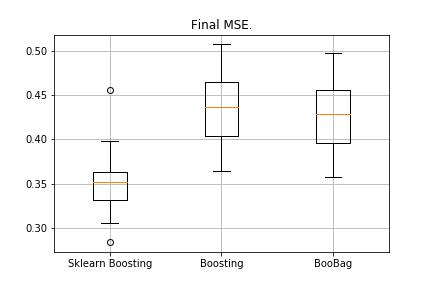
Nous ne pouvons pas encore vaincre l'analogue de Sklearn, car encore une fois, nous ne prenons pas en compte un grand nombre de paramètres qui sont utilisés dans cette méthode . Cependant, nous voyons que l'ensachage aide un peu.

Ne désespérons pas et passons à l'écriture de XGBoost.

4. XGBoost

Avant de continuer à lire, je vous conseille fortement de vous familiariser d'abord avec la vidéo suivante, qui explique très bien la théorie.

Rappelez-vous quelle erreur nous minimisons en boost normal:

$$

$$err (h) = \ sum_ {j = 1} ^ N L (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j))$$

XGBoost ajoute explicitement la régularisation à cette fonctionnalité d'erreur:

$$

$$err (h) = \ sum_ {j = 1} ^ NL (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j)) + \ sum_ {i = 1} ^ T \ oméga (a_i)$$

Comment considérer cette fonctionnalité? Tout d'abord, nous l'approximons à l'aide d'une série de Taylor de second ordre, où le nouvel algorithme est considéré comme un incrément le long duquel nous nous déplacerons, puis nous peignons déjà, en fonction du type de perte que nous avons:

$$$f (x + \ delta x) \ thickapprox f (x) + f (x) '\ delta x + 0.5 * f (x)' '(\ delta x) ^ 2$

Il est nécessaire de déterminer quel arbre nous considérerons comme mauvais et lequel est bon.

Rappelez-vous sur quel principe la régression est construite $$$L_2$-régularisation - plus les valeurs des coefficients avant la régression sont normales, pire elles doivent donc être aussi petites que possible.

Dans XGBoost, l'idée est très similaire: l'arbre est condamné à une amende si la somme de la norme des valeurs dans les feuilles est très grande. Par conséquent, la complexité de l'arbre est introduite comme suit:

$$

$$\ oméga (a) = \ gamma Z + 0,5 * \ sum_ {i = 1} ^ {Z} w_i ^ 2$$

$$$w$- valeurs dans les feuilles, $$$Z$- nombre de feuilles.

Il existe des formules de transition dans la vidéo, nous ne les afficherons pas ici. Tout se résume au fait que nous choisirons une nouvelle partition, maximisant le gain:

$$

$$Gain = \ frac {G_l ^ 2} {S_l ^ 2 + \ lambda} + \ frac {G_r ^ 2} {S_r ^ 2 + \ lambda} - \ frac {(G_l + G_r) ^ 2} {S_l ^ 2 + S_r ^ 2 + \ lambda} - \ gamma$$

Ici $$$\ gamma, \ lambda$Les paramètres numériques de régularisation, et $$$G_i, S_i$- les sommes correspondantes des première et deuxième dérivées pour cette partition.

Voilà, la théorie est très brièvement énoncée, les liens sont donnés, parlons maintenant de ce que seront les dérivés si nous travaillons avec MSE. C'est simple:

$$$mse (y, prédire) = (y - prédire) ^ 2 \\ \ nabla_ {prédire} mse (y, prédire) = prédire - y \\ \ nabla_ {prédire} ^ 2 mse (y, prédire) = 1$

Quand calculerons-nous le montant $$$G_i, S_i$, il suffit d'ajouter au premier $$$prédire - y$et le second est juste la quantité.

 %%cython -a import numpy as np cimport numpy as np cdef class RegressionTreeGain: cdef public int max_depth cdef public np.float64_t gain cdef public np.float64_t lmd cdef public np.float64_t gmm cdef public int feature_idx cdef public int min_size cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef public RegressionTreeGain left cpdef public RegressionTreeGain right def __init__(self, int max_depth=3, np.float64_t lmd=1.0, np.float64_t gmm=0.1, min_size=5): self.max_depth = max_depth self.gmm = gmm self.lmd = lmd self.left = None self.right = None self.feature_idx = -1 self.feature_threshold = 0 self.value = -1e9 self.min_size = min_size return def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef long idx = 0 cpdef long thres = 0 cpdef np.float64_t gl, gr, gn cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 cpdef np.float64_t best_gain = -self.gmm if self.value == -1e9: self.value = y.mean() base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 if self.max_depth <= 1: return dim_shape = X.shape[1] left_value = 0 right_value = 0 #    # -  -   mse, L = (y - pred)**2 # dL/dpred = pred - y,          - # dL^2/d^2pred = 1 - ,       for feat in range(dim_shape): idxs = np.argsort(X[:, feat]) gl,gr = y.sum(),0.0 N1, N2, thres = N, 0, 0 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] gl -= y[idx] gr += y[idx] #   gn = (gl**2) / (N1 + self.lmd) + (gr**2) / (N2 + self.lmd) gn -= ((gl + gr)**2) / (N1 + N2 + self.lmd) + self.gmm if thres < N - 1 and x == X[idxs[thres + 1], feat]: thres += 1 continue #     if (gn > best_gain) and (min(N1,N2) > self.min_size): flag = 1 best_gain = gn left_value = -gl / (N1 + self.lmd) right_value = -gr / (N2 + self.lmd) self.feature_idx = feat self.feature_threshold = x thres += 1 self.gain = best_gain if self.feature_idx == -1: return self.left = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd) self.left.value = left_value self.right = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd) self.right.value = right_value idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) #    if (self.left.left == None or self.right.left == None): if self.gain < 0.0: self.left = None self.right = None self.feature_idx = -1 def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

Une petite précision: pour rendre les formules dans les arbres à gain plus belles, en boost on entraîne la cible avec un signe moins.

Nous modifions légèrement notre boosting, rendons certains paramètres adaptatifs. Par exemple, si nous remarquons que la perte a commencé à atteindre un plateau, nous diminuons le taux d'apprentissage et augmentons max_depth pour les estimateurs suivants. Nous allons également ajouter un nouvel ensachage - nous allons maintenant augmenter le gainage des arbres avec le gain:

 class Bagging(): def __init__(self, max_depth = 3, min_size=5, n_samples = 10): self.max_depth = max_depth self.min_size = min_size self.n_samples = n_samples self.subsample_size = None self.list_of_Carts = [RegressionTreeGain(max_depth=self.max_depth, min_size=self.min_size) for _ in range(self.n_samples)] def get_bootstrap_samples(self, data_train, y_train): indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size)) samples_train = data_train[indices] samples_y = y_train[indices] return samples_train, samples_y def fit(self, data_train, y_train): self.subsample_size = int(data_train.shape[0]) samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train) for i in range(self.n_samples): self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1)) return self def predict(self, test_data): num_samples = test_data.shape[0] pred = [] for i in range(self.n_samples): pred.append(self.list_of_Carts[i].predict(test_data)) pred = np.array(pred).T return np.array([np.mean(pred[i]) for i in range(num_samples)]) 

 class GradientBoosting(): def __init__(self, n_estimators=100, learning_rate=0.2, max_depth=3, random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'): self.n_estimators = n_estimators self.max_depth = max_depth self.learning_rate = learning_rate self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]]) self.min_size = min_size self.loss_by_iter = [] self.trees_ = [] self.loss_by_iter_test = [] self.n_samples = n_samples self.base_tree = base_tree #  -       #   ,   lr   max_depth self.add_to_max_depth = 1 self.init_mse_board = 1.5 def fit(self, X, y): print (self.base_tree) self.X = X self.y = y b = self.initialization(y) prediction = b.copy() for t in tqdm_notebook(range(self.n_estimators)): if t == 0: resid = y else: resid = (y - prediction) if (mse(temp_resid,resid) < self.init_mse_board): self.init_mse_board /= 1.5 self.add_to_max_depth += 1 self.learning_rate /= 1.1 # print ('Alert!', t, self.add_to_max_depth) if self.base_tree == 'Bagging': tree = Bagging(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) resid = -resid if self.base_tree == 'Tree': tree = RegressionTreeFastMse(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) if self.base_tree == 'XGBoost': tree = RegressionTreeGain(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) resid = -resid tree.fit(X, resid) b = tree.predict(X).reshape([X.shape[0]]) # print (b.shape) self.trees_.append(tree) prediction += self.learning_rate * b temp_resid = resid return self def predict(self, X): #   –          pred = np.ones([X.shape[0]]) * np.mean(self.y) #    for t in range(self.n_estimators): pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]]) return pred 

5. Résultats

Par tradition, nous comparons les résultats:

 data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn er_boosting_bagging = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='Bagging')) er_boosting_xgb = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='XGBoost')) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=150,learning_rate=0.2)) %matplotlib inline data = [er_sklearn_boosting, er_boosting_xgb, er_boosting_bagging] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['GdbSklearn', 'Xgboost', 'XGBooBag']) plt.grid() plt.show() 

L'image sera la suivante:



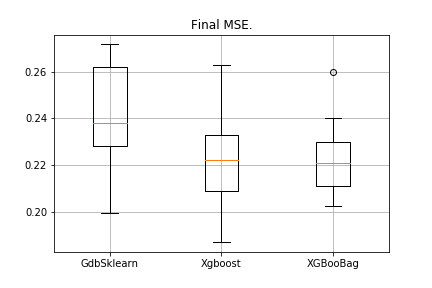
XGBoost a l'erreur la plus faible, mais XGBooBag a une erreur plus encombrée, ce qui est certainement mieux: l'algorithme est plus stable.

C’est tout. J'espère vraiment que le matériel présenté dans deux articles a été utile et que vous pourrez apprendre quelque chose de nouveau par vous-même. J'exprime une gratitude particulière à Dmitry pour ses commentaires complets et son code source, à Anton pour ses conseils et à Vladimir pour ses tâches difficiles à étudier.

Tout succès!