Fonctionnement du PageRank: implémentation en R via l'algèbre linéaire et la méthode d'alimentation

Bonjour, citoyens Habrovsk!

Je m'appelle Alex. Cette fois, j'ai diffusé depuis le lieu de travail dans ITAR-TASS.

Dans ce court texte, je vais vous présenter la méthode de calcul du PageRank © (ci-après je l'appellerai PR) en utilisant des exemples simples et compréhensibles, en langage R. L'algorithme est une propriété intellectuelle de Google, mais, en raison de son utilité pour les tâches d'analyse de données, de nombreuses tâches sont utilisées , qui peut être réduit à la recherche de grands nœuds dans le graphique et à leur classement par importance.

Mentionner une grande entreprise dans un message n'est pas une publicité.

Comme je ne suis pas un mathématicien professionnel, j'utilise - et vous recommande - cet article et ce tutoriel comme guide.

Compréhension intuitive des relations publiques

Comprendre comment cela fonctionne n'est pas difficile. Il existe un ensemble d'éléments interconnectés. Voici comment exactement ils sont connectés - c'est une question large: peut-être à travers des liens (comme Google), peut-être à travers des références les uns aux autres (presque les mêmes liens), les probabilités de transitions entre les éléments (matrice du processus de Markov) peuvent être a priori spécifiées sans préciser le physique sens de la communication. Je voudrais attribuer à ces éléments un certain critère d'importance, qui porterait des informations sur la probabilité que cet élément soit visité par une particule abstraite voyageant à travers le graphique dans le processus de diffusion.

Ça ne semble pas très clair. Il est plus facile d'imaginer un gars utilisant un ordinateur portable avec un coquelicot , surfant sur les pages de résultats de recherche, fumant un narguilé, suivant des liens d'une page à une autre et apparaissant de plus en plus souvent sur la même page (ou les mêmes pages).

Cela est dû au fait que certaines pages qu'il visite contiennent des informations si intéressantes dans la source d'origine que d'autres pages sont obligées de les réimprimer avec une indication du lien.

Un tel gars dans Google a été nommé surfeur aléatoire. Il est une particule en cours de diffusion: un changement de position discret sur le graphe au fil du temps. Et la probabilité avec laquelle il visite la page avec un temps de diffusion tendant vers l'infini est PR.

Implémentation simple du calcul PR

Soyons d'accord - nous travaillons avec 10 éléments, dans un si petit et confortable petit graphique.

# clear environment rm(list = ls()); gc() ## load libs library(data.table) library(magrittr) library(markovchain) ## dummy data number_nodes <- 10 node_names <- letters[seq_len(number_nodes)] set.seed(1) nodes <- sapply( seq_len(number_nodes), function(x) { paste( c( node_names[-x] , sample(node_names[-x], sample(1:5, 1), replace = T) ) , collapse = ' ' ) } ) names(nodes) <- node_names print( paste(nodes, collapse = '; ') ) ## make long dt dt <- data.table( citing_node = node_names , cited_node = nodes ) %>% .[, .(cited_node = unlist(strsplit(cited_node, ' '))), by = citing_node] %>% dcast( . , cited_node ~ citing_node , fun.aggregate = length ) dt apply(dt[,-1,with=F], 2, sum) ## affinity matrix A <- as.matrix(dt[, 2:dim(dt)[2]]) A <- sweep(A, 2, colSums(A), `/`) A[is.nan(A)] <- 0 rowSums(A) colSums(A) mark <- new("markovchain", transitionMatrix = t(A), states = node_names, name = "mark") plot(mark) 

Chacun des 10 éléments (nœuds) contient de 10 à 14 références à d'autres nœuds dans un ordre aléatoire, à l'exclusion de lui-même. Pour le moment, nous décidons simplement que les données mentionnées sont un lien web.

Il est clair qu'il peut arriver que certains éléments soient mentionnés plus souvent que d'autres. Regardez ça.

Soit dit en passant, je recommande d'utiliser le package data.table pour les expériences. En conjonction avec les principes de tidyverse, tout se passe efficacement et rapidement.

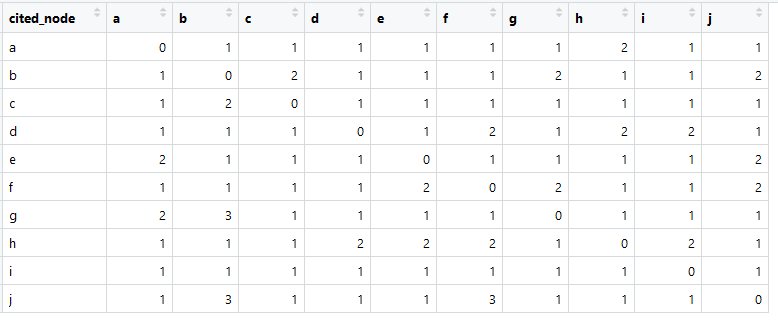
Voici à quoi ressemble notre matrice de liens (appelée en anglais le plus souvent la matrice d'adjacence).

La somme dans chaque colonne est supérieure à zéro, ce qui signifie qu'il existe une connexion entre chaque élément et un autre élément (cela est important pour une analyse plus approfondie).

> appliquer (dt [, - 1, avec = F], 2, somme)
abcdefghij
11 14 10 10 11 13 11 11 11 12

Sur la base de ce tableau, nous pouvons créer la matrice dite d'affinité, ou, à notre avis, la matrice de proximité (et elle est aussi appelée matrice de transition), que les mathématiciens appellent la matrice stochastique (matrice colonne-stochastique): source principale

Affectez-le à une variable nommée A.



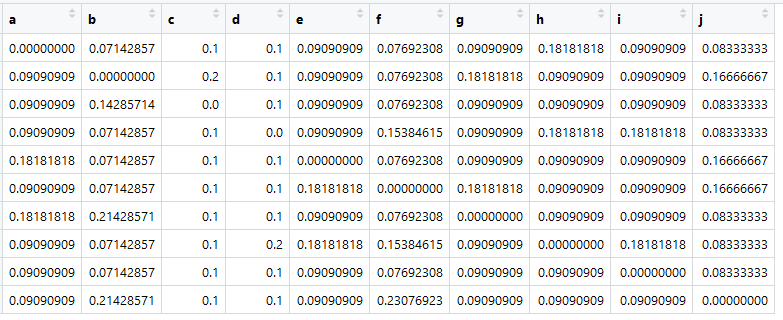
La chose la plus importante maintenant est que la somme dans toutes les colonnes est égale à un.

> colSums (A)
abcdefghij
1 1 1 1 1 1 1 1 1 1

Le voici - une matrice de transitions, c'est Markov, ce sont des similitudes. Les chiffres sont les probabilités de transitions d'un élément dans une colonne à un élément dans une ligne.

Ce ne sont bien sûr pas de véritables «similitudes». Le présent serait, par exemple, si l'on calcule le cosinus de l'angle entre la présentation des documents. Mais il est important que la matrice de transition soit réduite à des (pseudo-) probabilités afin que la somme sur chaque colonne soit égale à un.

Regardons le graphe de transition de Markov (notre A):



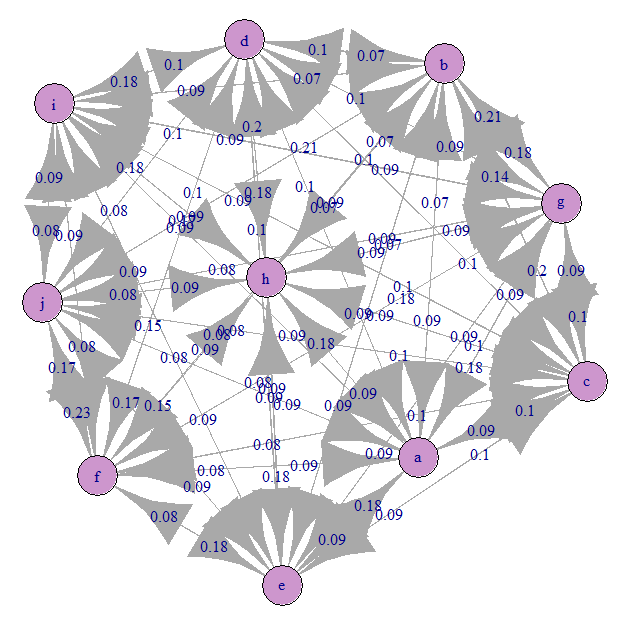
Tout est à peu près également confondu). En effet, nous avons spécifié des transitions équiprobables.

Et c'est maintenant le temps de la magie!

 ## calculate pagerank ei <- eigen(A) as.numeric(ei$values[1]) pr <- as.numeric(ei$vectors[,1] / sum(ei$vectors[,1])) sum(pr) names(pr) <- node_names print(round(pr, 2)) 

Pour une matrice stochastique A, la première valeur propre doit être égale à l'unité et le vecteur propre correspondant est le vecteur PageRank.

> impression (ronde (pr, 2))
abcdefghij
0,09 0,11 0,09 0,10 0,10 0,11 0,10 0,11 0,08 0,11

C'est le vecteur des valeurs PR - c'est le vecteur propre normalisé de la matrice de transition A correspondant à la valeur propre de cette matrice égale à l'unité - le vecteur propre dominant.

Vous pouvez maintenant classer les éléments. Mais en raison des spécificités de l'expérience, ils ont un poids très similaire.

Problèmes et leurs solutions en utilisant la méthode d'alimentation

La matrice de transition A peut ne pas satisfaire aux conditions de stochasticité.

Premièrement, il peut y avoir des éléments qui ne se réfèrent nulle part, c'est-à-dire en l'absence de rétroaction (ils peuvent s'y référer eux-mêmes). Pour les grands graphiques réels, c'est un problème probable. Cela signifie que l'une des colonnes de la matrice n'aura que des zéros. Dans ce cas, la solution via des vecteurs propres ne fonctionnera pas.

Google a résolu ce problème en remplissant une colonne avec une distribution de probabilité uniforme p = 1 / N. Où N est le nombre de tous les éléments.

 dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) 

Deuxièmement, le graphique peut contenir des éléments avec rétroaction, mais pas les autres éléments du graphique. C'est également un problème insurmontable pour l'algèbre linéaire en raison de la violation des hypothèses.

Il est résolu en introduisant une constante appelée facteur d'amortissement, qui indique la probabilité a priori d'une transition d'un élément à un autre, même s'il n'y a pas de liens physiques. En d'autres termes, la diffusion est possible dans n'importe quel état.

 d = 0.15 #damping factor (to ensure algorithm convergence) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix 

Si nous appliquons ces transformations à notre matrice, elles peuvent à nouveau être résolues par des vecteurs propres!

Troisièmement, la matrice ringarde peut ne pas être carrée, mais c'est critique! Je ne m'attarderai pas sur ce moment, car je crois que vous trouverez vous-même comment y remédier.

Mais il existe une méthode plus rapide et plus précise, qui est également plus économique en mémoire (ce qui peut être pertinent pour les grands graphiques): la méthode Power.

 ## pagerank function (tested on example from tutorial) rm(pagerank_func) pagerank_func <- function( A #transition matrix , eps = 0.00001 #sufficiently small error , d = 0.15 #damping factor (to ensure algorithm convergence) ) { dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix rank = as.numeric(rep(1 / dim.1, dim.1)) ## iterate until convergence while( sum( (rank - M %*% rank) ^ 2 ) > eps ) { rank <- M %*% rank } return(rank) } pr2 <- pagerank_func(A) pr2=as.vector(pr2) names(pr2)=node_names 

Voila!

> impression (ronde (pr, 2))
abcdefghij
0,09 0,11 0,09 0,10 0,10 0,11 0,10 0,11 0,08 0,11
> impression (ronde (pr2, 2))
abcdefghij
0,09 0,11 0,09 0,10 0,10 0,11 0,10 0,11 0,08 0,11

Sur cela, je terminerai le tutoriel. J'espère que vous le trouverez utile.

J'ai oublié de dire que pour construire une matrice de transitions (probabilités), vous pouvez utiliser la similitude des textes, le nombre de références, le fait d'un lien, et d'autres métriques qui conduisent à des pseudo-probabilités ou sont des probabilités. Un exemple assez intéressant est le classement des phrases dans le texte sur la matrice de similitude des sacs de mots tf-idf pour mettre en évidence la phrase résumant l'ensemble du texte. Il peut y avoir d'autres utilisations créatives des relations publiques.

Je recommande d'essayer par vous-même de jouer avec la matrice de transition et de vous assurer d'obtenir des valeurs PR sympas, qui sont également assez faciles à interpréter.

Si vous voyez des inexactitudes ou des erreurs avec moi - indiquez dans les commentaires ou le message, et je corrigerai tout.

Tout le code est compilé ici:


PS: toute cette idée est aussi facilement implémentée dans d'autres langages, du moins en Python, j'ai tout fait sans difficulté.