Comment le code-barres est-il organisé?

Bonjour, Habr!

Une personne moderne rencontre chaque jour des codes-barres, sans même y penser. Lorsque nous achetons des produits au supermarché, leurs codes sont lus précisément à l'aide d'un code-barres. Aussi des colis, des marchandises dans des entrepôts, etc. Cependant, peu de gens savent comment cela fonctionne vraiment.

Comment le code-barres est-il organisé et qu'est-ce qui est encodé dans cette image?



Essayons de le comprendre, en même temps, nous allons écrire un décodeur de ces codes.

Présentation

L'utilisation de codes-barres a une longue histoire. Les premières tentatives d'automatisation ont commencé dans les années 1950; un brevet pour un lecteur de code a été obtenu en 1952. L'ingénieur impliqué dans le tri des wagons sur la voie ferrée a souhaité simplifier le processus. L'idée était évidente: coder le nombre à l'aide de bandes et les lire à l'aide de photocellules. En 1962, les codes ont commencé à être officiellement utilisés pour identifier les voitures sur le chemin de fer américain (système KarTrak ), en 1968, le projecteur a été remplacé par un faisceau laser, ce qui a augmenté la précision et réduit la taille du lecteur. En 1973, le format «Universal Product Code» est apparu et, en 1974, le premier produit a été vendu à l'aide d'un scanner de code (le chewing-gum de Wrigley est aux États-Unis;) dans un supermarché. En 1984, un tiers des magasins utilisaient des banderoles, mais en Russie, ils ont commencé à être utilisés vers les années 90.

Beaucoup de codes différents sont utilisés pour différentes tâches, par exemple, la séquence "12345678" peut être représentée de cette manière (et ce n'est pas tout):



Commençons l'analyse syntaxique au niveau du bit. De plus, tout ce qui est décrit ci-dessous fera référence au formulaire «Code-128» - simplement parce que son format est assez simple et direct. Ceux qui souhaitent expérimenter avec d'autres espèces peuvent ouvrir un générateur en ligne et voir par eux-mêmes.

À première vue, le code à barres semble être juste une séquence aléatoire de lignes, en fait, sa structure est clairement fixée:



1 - Espace vide nécessaire pour identifier clairement le début du code
2 - Symbole de départ. Pour le Code-128, 3 options sont possibles (appelées A, B et C): 11010000100, 11010010000 ou 11010011100, elles correspondent à différentes tables de codes (pour plus de détails, voir Wikipedia ).
3 - En fait, le code contenant les données dont nous avons besoin
4 - Somme de contrôle
5 - Symbole d'arrêt. Pour Code-128, il s'agit de 1100011101011.
6 (1) - Espace vide.

Maintenant, comment les bits sont encodés. Tout est très simple ici - si vous prenez la largeur de la ligne la plus mince comme «1», alors la ligne à double largeur donnera le code «11», un triple «111», et ainsi de suite. L'espace vide sera "0" ou "00" ou "000" selon le même principe. Ceux qui le souhaitent peuvent comparer le code de départ dans l'image pour s'assurer que la règle est respectée.

Vous pouvez maintenant commencer la programmation.

Obtenez la séquence de bits

En principe, c'est la partie la plus difficile, et bien sûr, algorithmiquement, elle peut être mise en œuvre de différentes manières. Je ne suis pas sûr que l'algorithme ci-dessous soit optimal, mais il suffit amplement pour une étude de cas.

Tout d'abord, chargez l'image, étirez-la en largeur, prenez une ligne horizontale à partir du milieu de l'image, convertissez-la en n / b et chargez-la en tant que tableau.

from PIL import Image import numpy as np import matplotlib.pyplot as plt image_path = "barcode.jpg" img = Image.open(image_path) width, height = img.size basewidth = 4*width img = img.resize((basewidth, height), Image.ANTIALIAS) hor_line_bw = img.crop((0, int(height/2), basewidth, int(height/2) + 1)).convert('L') hor_data = np.asarray(hor_line_bw, dtype="int32")[0] 

Sur le code-barres, "1" correspond au noir, et en RVB, au contraire, 0, donc le tableau doit être inversé. Dans le même temps, nous calculons la valeur moyenne.

 hor_data = 255 - hor_data avg = np.average(hor_data) plt.plot(hor_data) plt.show() 

Nous démarrons le programme pour nous assurer que le code-barres est correctement chargé:



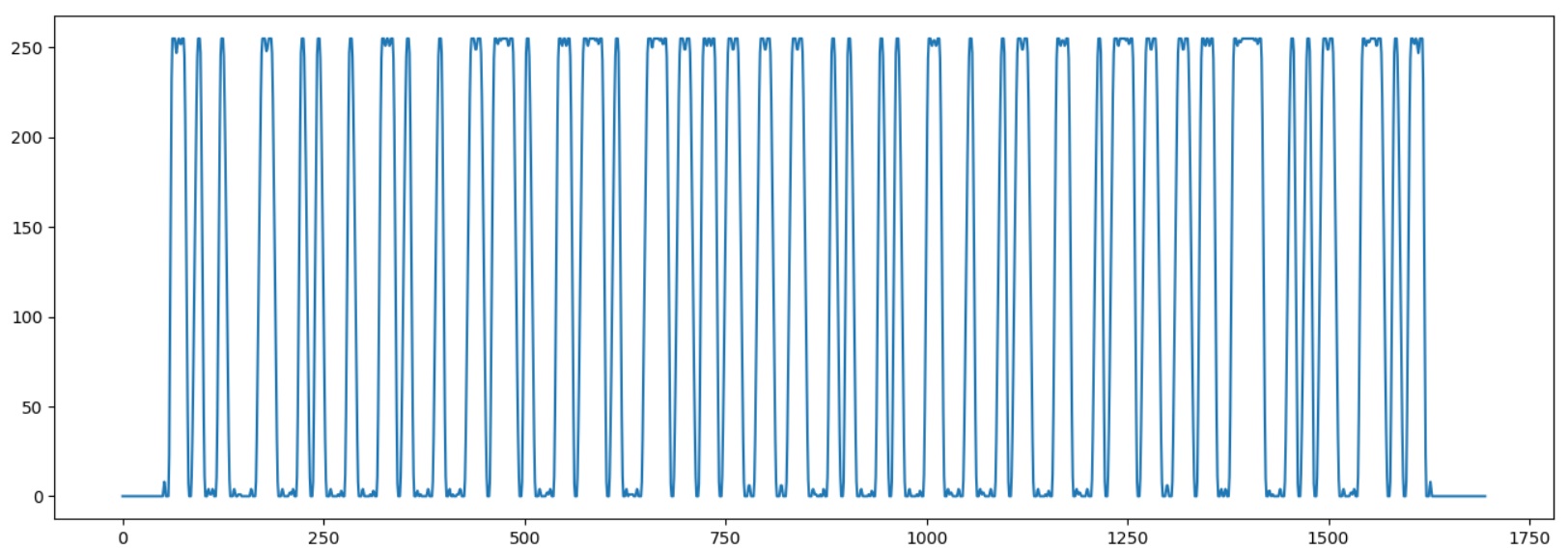
Vous devez maintenant déterminer la largeur d'un "bit". Pour ce faire, nous mettons en évidence le début de la séquence de départ "1101", en enregistrant les moments de transition du graphe à travers la ligne médiane.

 pos1, pos2 = -1, -1 bits = "" for p in range(basewidth - 2): if hor_data[p] < avg and hor_data[p + 1] > avg: bits += "1" if pos1 == -1: pos1 = p if bits == "101": pos2 = p break if hor_data[p] > avg and hor_data[p + 1] < avg: bits += "0" bit_width = int((pos2 - pos1)/3) 

Nous enregistrons uniquement les transitions par le milieu, de sorte que le code "1101" sera écrit "101", mais cela nous suffit pour connaître sa largeur en pixels.

Maintenant, le décodage réel. Nous trouvons la transition suivante par le milieu et déterminons le nombre de bits qui tombent dans l'intervalle. Comme la correspondance n'est pas absolue (le code peut être légèrement incurvé ou étiré), nous utilisons l'arrondi.

 bits = "" for p in range(basewidth - 2): if hor_data[p] > avg and hor_data[p + 1] < avg: interval = p - pos1 cnt = interval/bit_width bits += "1"*int(round(cnt)) pos1 = p if hor_data[p] < avg and hor_data[p + 1] > avg: interval = p - pos1 cnt = interval/bit_width bits += "0"*int(round(cnt)) pos1 = p 

Je ne sais pas si c'est la meilleure option, peut-être y a-t-il une meilleure façon, ceux qui le souhaitent peuvent écrire dans les commentaires.

Si tout a été fait correctement, nous obtenons alors la séquence de sortie suivante:

11010010000110001010001000110100010001101110100011011101000111011011
01100110011000101000101000110001000101100011000101110110011011001111
00010101100011101011

Décodage

Ici, en principe, il n'y a pas de difficultés. Les caractères du code 128 sont codés avec un code à 11 bits, qui a 3 variétés (A, B et C) et peuvent stocker soit des codages de caractères différents soit des nombres de 00 à 99.

Dans notre cas, le début de la séquence est 11010010000, ce qui correspond au «Code B». Il était terriblement cassé de piloter manuellement tous les codes de Wikipedia, donc le tableau a été simplement copié à partir du navigateur et son analyse a également été effectuée en Python (indice: ce n'est pas nécessaire pour la production).

  CODE128_CHART = """ 0 _ _ 00 32 S 11011001100 212222 1 ! ! 01 33 ! 11001101100 222122 2 " " 02 34 " 11001100110 222221 3 # # 03 35 # 10010011000 121223 ... 93 GS } 93 125 } 10100011110 111341 94 RS ~ 94 126 ~ 10001011110 131141 103 Start Start A 208 SCA 11010000100 211412 104 Start Start B 209 SCB 11010010000 211214 105 Start Start C 210 SCC 11010011100 211232 106 Stop Stop - - - 11000111010 233111""".split() SYMBOLS = [value for value in CODE128_CHART[6::8]] VALUESB = [value for value in CODE128_CHART[2::8]] CODE128B = dict(zip(SYMBOLS, VALUESB)) 

Maintenant, la chose la plus simple reste. Nous divisons notre séquence de bits en blocs de 11 caractères:

 sym_len = 11 symbols = [bits[i:i+sym_len] for i in range(0, len(bits), sym_len)] 

Enfin, nous formons la ligne et l'affiche à l'écran:

 str_out = "" for sym in symbols: if CODE128A[sym] == 'Start': continue if CODE128A[sym] == 'Stop': break str_out += CODE128A[sym] print(" ", sym, CODE128A[sym]) print("Str:", str_out) 

Je ne donnerai pas la réponse à ce qui est encodé dans le tableau, que ce soit un devoir pour les lecteurs (l'utilisation de programmes prêts à l'emploi pour smartphones sera considérée comme de la triche :).

Le code n'implémente pas non plus la vérification CRC, ceux qui le souhaitent peuvent le faire eux-mêmes.

Bien sûr, l'algorithme est imparfait et a été écrit en une demi-heure. À des fins plus professionnelles, il existe des bibliothèques prêtes à l'emploi, par exemple pyzbar . Le code utilisant une telle bibliothèque ne prendra que 4 lignes:

 from pyzbar.pyzbar import decode img = Image.open(image_path) decode = decode(img) print(decode) 

(vous devez d'abord installer la bibliothèque en entrant la commande pip install pyzbar)

Addition : vinograd19 a écrit dans les commentaires sur le comptage CRC:

L'histoire du chiffre de contrôle est intéressante. Il est né évolutivement.
Le chiffre de contrôle est nécessaire afin d'éviter un décodage incorrect. Si le code à barres était 1234 et qu'il a été reconnu comme 7234, vous avez besoin d'une validation qui empêchera le remplacement de 1 par 7. La validation peut être inexacte de sorte qu'au moins 90% des numéros invalides soient déterminés à l'avance.

1ère approche: Prenons simplement le montant. Pour que le reste de la division par 10 soit 0. Eh bien, c'est-à-dire que les 12 premiers caractères portent une charge d'informations, et le dernier chiffre est sélectionné de sorte que la somme des chiffres soit divisée par 10. Décodez la séquence, si la somme n'est pas divisible par dix, cela signifie décodé avec un bogue et vous devez le faire cette fois encore. Par exemple, le code 1234 est valide. 1 + 2 + 3 + 4 = 10. Le code 1216 est également valide, mais 1218 ne l'est pas.

Cela évite les problèmes d'automatisation. Cependant, au moment de la création des codes-barres, il y a eu un repli sous la forme de la saisie d'un nombre sur les touches. Et il y a un mauvais cas: si vous changez l'ordre des deux chiffres, la somme de contrôle ne change pas, et c'est mauvais. Autrement dit, si le code à barres 1234 a été martelé comme 2134, la somme de contrôle convergera, mais nous avons entré le mauvais numéro. Il s'avère que le mauvais ordre des numéros est un cas courant si vous frappez rapidement les clés.

2ème approche. Eh bien, rendons le montant un peu plus compliqué. Pour que les chiffres sur les places paires soient pris en compte deux fois. Ensuite, lors du changement de commande, le montant ne convergera certainement pas vers celui souhaité. Par exemple, le code 2364 est valide (2 + 3 + 3 + 6 + 4 + 4 = 20) et le code 3264 n'est pas valide (3+ 2 + 2 + 6 + 4 + 4 = 19). Mais voici un autre mauvais exemple de conduite. Certains claviers sont tels que dix chiffres sont disposés sur deux rangées. la première ligne est 12345 et en dessous la deuxième deuxième ligne est 67890. Si, au lieu de la touche "1", appuyez sur la touche "2" vers la droite, la somme de contrôle empêchera la saisie incorrecte. Mais si au lieu de la touche «1», appuyez sur la touche «6» ci-dessous, il ne peut pas avertir. Après tout, 6 = 1 + 5, et dans le cas où ce chiffre est à un même endroit lors du calcul de la somme de contrôle, nous avons 2 * 6 = 2 * 1 + 2 * 5. C'est-à-dire que la somme de contrôle a augmenté exactement de 10, donc son dernier chiffre n'a pas changé. Par exemple, les sommes de contrôle des codes 2134 et 2634 sont identiques. La même erreur se produira si nous appuyons sur 7 au lieu de 2, au lieu de 3 sur 8, etc.

3ème approche. Ok, reprenons la somme, seuls les nombres aux endroits pairs seront pris en compte ... trois fois. Autrement dit, le code 1234565 est valide, car 1 + 2 * 3 + 3 + 4 * 3 + 5 + 6 * 3 +5 = 50.

La méthode décrite est devenue la norme pour calculer la somme de contrôle EAN13 avec quelques corrections: le nombre de chiffres est devenu fixe et égal à 13, où le 13e est la même somme de contrôle. Les nombres sur les endroits impairs sont comptés trois fois, sur ceux pairs - une fois.

Conclusion

Comme vous pouvez le voir, même une chose aussi simple qu'un code à barres contient beaucoup de choses intéressantes. Au fait, un autre hack de vie pour ceux qui ont lu jusqu'ici - le texte sous le code-barres (le cas échéant) duplique complètement son contenu. Ceci est fait de sorte qu'en cas de code illisible, l'opérateur puisse le saisir manuellement. Donc, pour découvrir le contenu d'un code-barres est généralement simple - il suffit de regarder le texte en dessous.

Comme suggéré dans les commentaires, le plus populaire dans le commerce est le code EAN-13, le codage binaire est le même là-bas, et ceux qui le souhaitent peuvent voir la structure des caractères eux-mêmes .

Si les lecteurs n'ont pas perdu tout intérêt, vous pouvez considérer séparément les codes QR.

Merci de votre attention.