🏇🏽 👨‍🎤 😭 Renforcement de l'apprentissage en profondeur: ping pong pixel brut ⚒️ 💹 👩🏼‍🚒

Il s'agit d'un article attendu depuis longtemps sur l'apprentissage par renforcement (RL). RL est un sujet cool!

Vous savez peut-être que les ordinateurs peuvent désormais apprendre automatiquement à jouer aux jeux ATARI (en obtenant des pixels de jeu bruts à l'entrée!). Ils ont battu les champions du monde dans le jeu de Go , les quadrupèdes virtuels apprennent à courir et à sauter , et les robots apprennent à effectuer des tâches de manipulation complexes qui défient la programmation explicite. Il s'avère que toutes ces réalisations ne sont pas complètes sans RL. J'ai également été intéressé par RL au cours de la dernière année: j'ai travaillé avec le livre de Richard Sutton (référence approximative: remplacé) , lu le cours de David Silver , assisté aux conférences de John Schulman , écrit la bibliothèque RL sur Javascript et effectué un stage chez DeepMind en été, travaillant dans un groupe DeepRL, et plus récemment, dans le développement d' OpenAI Gym , est la nouvelle boîte à outils RL. Donc, bien sûr, je fais partie de cette vague depuis au moins un an, mais je n'ai pas encore pris la peine d'écrire une note sur pourquoi RL est d'une grande importance, de quoi il s'agit, comment tout cela se développe.

Exemples d'utilisation de Deep Q-Learning. De gauche à droite: le réseau neuronal joue ATARI, le réseau neuronal joue AlphaGo, le robot plie Lego, le quadrupède virtuel court autour des obstacles virtuels.

Il est intéressant de réfléchir à la nature des progrès récents en matière de RL. Je voudrais noter quatre facteurs distincts affectant le développement de l'IA:

Vitesse de calcul (GPU, dispositifs spéciaux ASIC, loi de Moore)
Données suffisantes sous une forme utilisable (par exemple ImageNet)
Algorithmes (recherche et idées, par exemple backprop, CNN, LSTM)
Infrastructure (Linux, TCP / IP, Git, ROS, PR2, AWS, AMT, TensorFlow, etc.).

Tout comme en vision par ordinateur, les progrès en RL évoluent ... mais pas autant que cela puisse paraître. Par exemple, en vision par ordinateur, le réseau neuronal AlexNet 2012 est une version augmentée en profondeur et en largeur du réseau neuronal ConvNets des années 1990. De même, ATARI Deep Q-Learning 2013 est une implémentation de l'algorithme Q-Learning standard que vous pouvez trouver dans le livre classique de Richard Sutton de 1998. De plus, AlphaGo utilise la technique du gradient politique et la recherche d'arbre Monte Carlo (SCTM) sont également de vieilles idées ou leurs combinaisons. Bien sûr, il faut beaucoup de compétences et de patience pour les faire fonctionner, et de nombreux paramètres délicats ont été développés en plus des anciens algorithmes. Mais en première approximation, le principal moteur des progrès récents n'est pas les nouveaux algorithmes et idées, mais l'intensification des calculs, des données suffisantes et une infrastructure mature.

Revenons maintenant à RL. Beaucoup de gens ne peuvent pas croire que nous pouvons enseigner à un ordinateur comment jouer à des jeux ATARI à un niveau humain en utilisant des pixels bruts à partir de zéro et en utilisant le même algorithme d'auto-apprentissage. En même temps, chaque fois que je ressens un écart - à quel point cela semble magique et à quel point c'est vraiment simple à l'intérieur.

L'approche de base que nous utilisons est en fait assez stupide. Quoi qu'il en soit, je voudrais vous présenter la technique Policy Gradient (PG), notre choix par défaut préféré pour résoudre les problèmes avec RL en ce moment. Vous pouvez être curieux de savoir pourquoi, à la place, je ne peux pas imaginer DQN, qui est un algorithme RL alternatif et mieux connu qui est également utilisé dans la formation ATARI . Il s'avère que bien que le Q-Learning soit connu, il n'est pas si parfait. La plupart des gens choisissent d'utiliser Policy Gradient, y compris les auteurs de l' article DQN original, qui ont montré qu'avec un bon réglage, Policy Gradient fonctionne encore mieux que Q-Learning. PG est préférable car il est explicite: il existe une politique claire et une approche cohérente qui optimise directement les récompenses attendues. À titre d'exemple, nous allons apprendre à jouer à ATARI Pong: à partir de zéro, à partir de pixels bruts à travers un gradient de politique avec un réseau de neurones. Et nous allons mettre tout cela dans 130 lignes de Python. ( Lien essentiel ) Voyons comment cela se fait.

Ci-dessus: Ping Pong. Ci-dessous: Présentation du ping-pong comme cas particulier du processus décisionnel de Markov (MDP) : chaque sommet du graphique correspond à un certain état du jeu, et les bords déterminent les probabilités de transition vers d'autres états. Chaque côte détermine également la récompense. Le but est de trouver le meilleur chemin à partir de n'importe quel état pour maximiser la récompense

Jouer au ping-pong est un excellent exemple d'un défi RL. Dans la version ATARI 2600, nous jouerons nous-mêmes une raquette. Une autre raquette est contrôlée par un algorithme intégré. Nous devons frapper la balle pour que l'autre joueur n'ait pas le temps de la frapper. J'espère qu'il n'est pas nécessaire d'expliquer ce qu'est le Ping Pong. À un niveau bas, le jeu fonctionne comme suit: nous obtenons un cadre d'image - un tableau d'octets 210x160x3, et décidons si nous voulons déplacer la raquette UP ou DOWN. Autrement dit, nous n'avons que deux choix pour gérer le jeu. Après chaque choix, le simulateur de jeu effectue son action et nous donne une récompense: soit +1 récompense si le ballon a dépassé la raquette de l'adversaire, soit -1 si nous avons raté le ballon. Sinon 0. Et, bien sûr, notre objectif est de déplacer la raquette afin que nous obtenions autant de récompenses que possible.

Lorsque vous envisagez une solution, n'oubliez pas que nous allons essayer de faire si peu d'hypothèses sur le pong, car ce n'est pas particulièrement important dans la pratique. Nous prenons beaucoup plus de choses en compte dans les tâches à grande échelle, telles que la manipulation de robots, l'assemblage et la navigation. Pong est juste un cas de test amusant avec lequel nous jouons pendant que nous découvrons comment écrire des systèmes d'IA très généraux qui peuvent un jour effectuer des tâches utiles arbitraires.

Réseau de neurones comme politique RL . Premièrement, nous allons déterminer la soi-disant politique que notre joueur (ou «agent») met en œuvre. ((*) «Agent», «environnement» et «politique d'agent» sont des termes standard de la théorie RL). La fonction politique dans notre cas est un réseau de neurones. Elle acceptera l'état du jeu à l'entrée et à la sortie elle décidera quoi faire - monter ou descendre. Comme bloc de calcul simple préféré, nous utiliserons un réseau neuronal à deux couches qui prend des pixels d'image bruts (total de 100800 nombres (210 * 160 * 3)) et produit un nombre unique indiquant la probabilité de déplacer la raquette vers le haut. Veuillez noter que l'utilisation de la politique stochastique est standard, ce qui signifie que nous ne produisons que la probabilité d'un mouvement à la hausse. Pour obtenir le mouvement réel, nous utiliserons cette probabilité. La raison de cela deviendra plus claire lorsque nous parlerons de formation.

Notre fonction politique consistant en un réseau neuronal à 2 couches entièrement connecté

Plus précisément, supposons qu'à l'entrée, nous obtenons un vecteur X, qui contient un ensemble de pixels prétraités. Ensuite, nous devons calculer en utilisant python \ numpy:

h = np.dot(W1, x) # compute hidden layer neuron activations h[h<0] = 0 # ReLU nonlinearity: threshold at zero logp = np.dot(W2, h) # compute log probability of going up p = 1.0 / (1.0 + np.exp(-logp)) # sigmoid function (gives probability of going up)

Dans ce fragment, W1 et W2 sont deux matrices que nous initialisons au hasard. Nous n'utilisons pas de parti pris, car nous le voulions. Notez qu'au final, nous utilisons la non-linéarité du sigmoïde, ce qui réduit la probabilité de sortie à la plage [0,1]. Intuitivement, les neurones dans une couche cachée (dont les poids sont situés dans W1) peuvent détecter divers scénarios de jeu (par exemple, la balle est au-dessus et notre raquette est au milieu), et les poids dans W2 peuvent alors décider si nous devons augmenter dans chaque cas ou vers le bas. Les W1 et W2 aléatoires initiaux, bien sûr, provoqueront d'abord des spasmes et des convulsions chez notre neuro-joueur, ce qui l'égalera comme un imbécile autiste aux commandes d'un avion. La seule tâche maintenant est donc de trouver W1 et W2, ce qui conduit à un bon jeu!

Il y a une remarque à propos du prétraitement des pixels - idéalement, vous devez transférer au moins 2 images sur le réseau neuronal afin qu'il puisse détecter les mouvements. Mais pour simplifier la situation, nous appliquerons la différence de deux images. Autrement dit, nous soustraireons les trames actuelles et précédentes et n'appliquerons alors la différence qu'à l'entrée du réseau neuronal.

Cela ressemble à quelque chose d'impossible. À ce stade, j'aimerais que vous compreniez la complexité du problème RL. Nous obtenons 100 800 nombres (210x160x 3) et les envoyons à notre réseau de neurones qui met en œuvre la politique du joueur (qui, incidemment, comprend facilement environ un million de paramètres dans les matrices W1 et W2). Supposons qu'à un moment donné, nous décidions de monter. Le simulateur de jeu peut répondre que cette fois nous obtiendrons 0 récompenses et nous donnerons encore 100 800 numéros pour la prochaine image. Nous pouvons répéter ce processus des centaines de fois avant d'obtenir une récompense non nulle! Par exemple, supposons que nous ayons finalement obtenu une récompense +1. C'est merveilleux, mais comment alors dire - qu'est-ce qui a mené à cela? Était-ce l'action que nous avons faite tout à l'heure? Ou peut-être 76 images en arrière? Ou peut-être que cela a d'abord été associé à l'image 10, puis nous avons fait quelque chose de bien dans l'image 90? Et comment savoir - lequel des millions de "stylos" tourner afin d’obtenir un succès encore plus grand à l’avenir? Nous appelons cela la tâche de déterminer le coefficient de confiance dans certaines actions. Dans le cas spécifique du pong, nous savons que nous obtenons +1 si le ballon dépasse l'adversaire. La vraie raison est que nous avons accidentellement botté le ballon le long d'un bon chemin à quelques images en arrière, et chaque action ultérieure que nous avons effectuée ne l'a pas affectée du tout. En d'autres termes, nous sommes confrontés à un problème de calcul très complexe, et tout semble plutôt sombre.

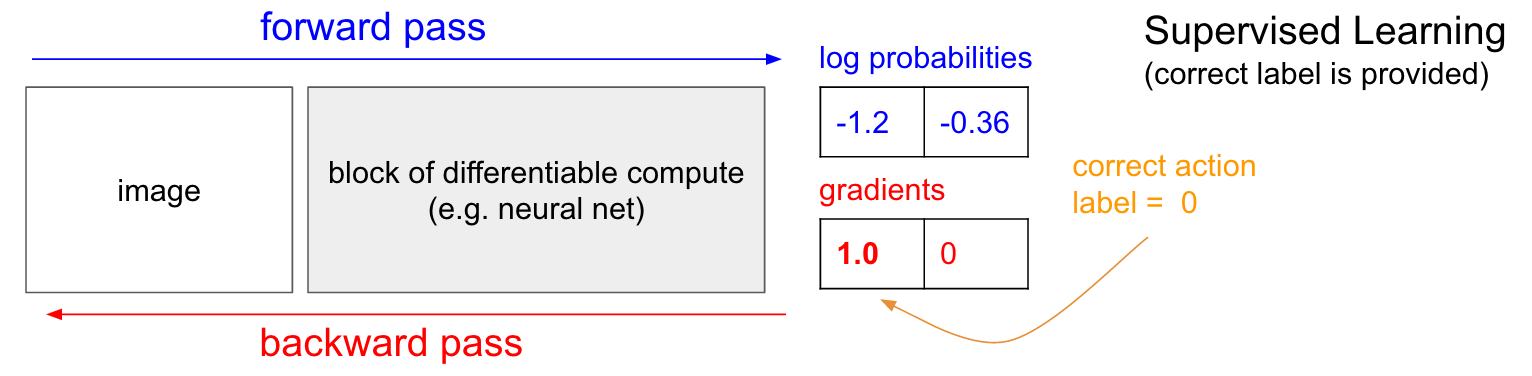
Formation avec un professeur. Avant de nous plonger dans le gradient de la politique (PG), je voudrais rappeler brièvement l'enseignement avec un enseignant, car, comme nous le verrons, RL est très similaire. Reportez-vous au tableau ci-dessous. Dans l'enseignement ordinaire avec un professeur, nous transférerons l'image sur le réseau et recevrons en sortie des probabilités numériques pour les classes. Par exemple, dans notre cas, nous avons deux classes: UP et DOWN. J'utilise les probabilités logarithmiques (-1,2, -0,36) au lieu des probabilités au format 30% et 70%, car nous optimisons la probabilité logarithmique de la bonne classe (ou étiquette). Cela rend les calculs mathématiques plus élégants et équivaut à optimiser la probabilité juste, car le logarithme est monotone.

En formation avec un professeur, nous aurons un accès instantané à la bonne classe (label). Au stade de la formation, ils nous diront exactement quelle bonne étape est nécessaire en ce moment (disons que c'est UP, étiquette 0), bien que le réseau neuronal puisse penser différemment. Par conséquent, nous calculons le gradient

$\ nabla_ {W} \ log p (y = UP \ mid x)$ pour modifier les paramètres réseau. Ce gradient nous indique simplement comment nous devons modifier chacun de nos millions de paramètres afin que le réseau soit légèrement plus susceptible de prévoir UP dans la même situation. Par exemple, l'un des millions de paramètres du réseau peut avoir un gradient de -2,1, ce qui signifie que si nous augmentions ce paramètre d'une petite valeur positive (par exemple, 0,001), la probabilité logarithmique de UP diminuerait de 2,1 * 0,001. (diminution due au signe négatif). Si nous appliquons le gradient puis mettons à jour le paramètre à l'aide de l'algorithme de rétropropagation, alors, oui, notre réseau donnera une forte probabilité de UP lorsqu'il verra la même image ou une image très similaire à l'avenir.

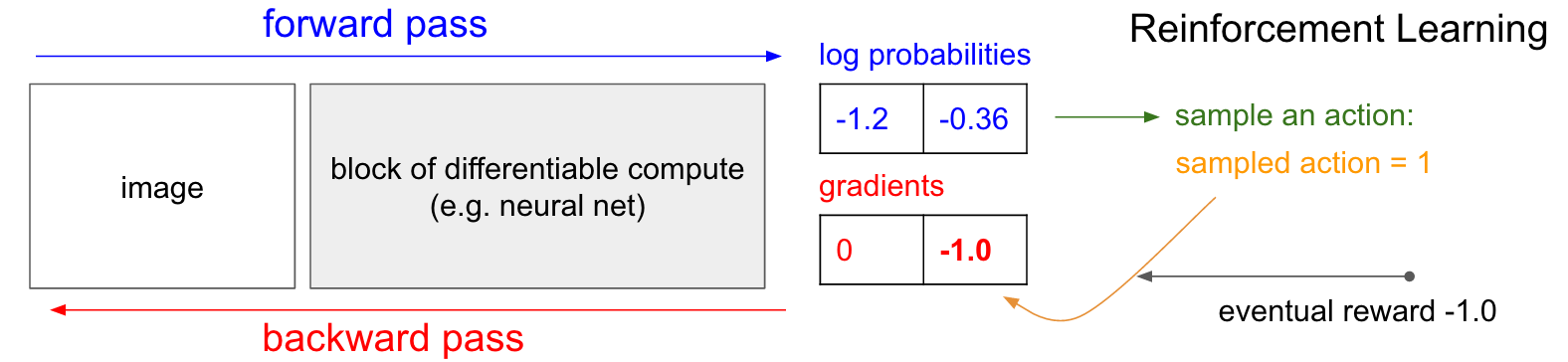
Gradients de politique (PG) . OK, mais que faisons-nous si nous n'avons pas le bon label de formation de renforcement? Voici une solution pour PG (reportez-vous à nouveau au schéma ci-dessous). Notre réseau de neurones a calculé la probabilité d'une augmentation de 30% (logprob -1,2) et d'une baisse de 70% (logprob -0,36). Maintenant, nous faisons une sélection à partir de cette distribution et spécifions quelle action nous allons faire. Par exemple, ils ont choisi DOWN et envoyé cette action au simulateur de jeu. À ce stade, faites attention à un fait intéressant: nous pourrions immédiatement calculer et appliquer le gradient pour l'action DOWN, comme nous l'avons fait dans l'enseignement avec un enseignant, et ainsi rendre le réseau plus susceptible d'exécuter l'action DOWN à l'avenir. Ainsi, nous pouvons immédiatement apprécier et mémoriser ce gradient. Mais le problème est que pour le moment nous ne le savons pas encore - est-ce bon de descendre? Mais la chose la plus intéressante est que nous pouvons simplement attendre un peu et appliquer le gradient plus tard! À Pong, nous pouvons attendre la fin de la partie, puis prendre la récompense que nous avons reçue (soit +1 si nous avons gagné, soit -1 si nous avons perdu), et la saisir comme facteur de gradient. Donc, si nous introduisons -1 pour la probabilité DOWN et faisons la propagation arrière, nous reconstruirons les paramètres du réseau afin qu'il soit moins susceptible d'exécuter l'action DOWN à l'avenir lorsqu'elle rencontrera la même image, car l'adoption de cette action nous a fait perdre le jeu. Autrement dit, nous devrons en quelque sorte nous souvenir de toutes les actions (entrées et sorties du réseau neuronal) dans un épisode du jeu et, sur la base de ce tableau, tordre le réseau neuronal presque de la même manière que dans l'enseignement avec un enseignant.

Et c'est tout ce qui est nécessaire: nous avons une politique stochastique qui choisit les actions, puis à l'avenir, les actions qui conduisent finalement à de bons résultats sont encouragées, et les actions qui conduisent à de mauvais résultats ne sont pas encouragées. De plus, la récompense ne devrait même pas être +1 ou -1 si nous gagnons finalement la partie. Il peut s'agir d'une valeur arbitraire de même signification. Par exemple, si tout fonctionne très bien, la récompense pourrait être 10,0, que nous utilisons ensuite comme gradient pour démarrer la rétropropagation backprop. C'est la beauté des réseaux de neurones. Leur utilisation peut sembler un canular: vous êtes autorisé à avoir 1 million de paramètres intégrés dans 1 téraflop de calculs, et vous pouvez faire apprendre au programme à faire des choses arbitraires avec la descente de gradient stochastique (SGD). Ça ne devrait pas marcher, mais c'est drôle que nous vivions dans un univers où ça marche.

Si nous jouions à des jeux de société simples, comme des dames, la commande serait à peu près la même. Il existe une différence notable par rapport aux algorithmes d'écrêtage minimax ou alpha-bêta. Dans ces algorithmes, le programme regarde en avant, connaissant les règles du jeu, et analyse des millions de positions. Dans l'approche RL, seuls les mouvements réellement effectués sont analysés. Dans le même temps, le réseau neuronal ne regarde pas vers l'avant, car il ne sait rien des règles du jeu.

Ordre d'entraînement en détail. Nous créons et initialisons un réseau de neurones avec certains W1, W2 et jouons 100 parties de pong (nous l'appelons le «rodage» de la politique, les déploiements de politiques). Supposons que chaque jeu se compose de 200 images, donc au total, nous avons pris 100 * 200 = 20 000 décisions de monter ou de descendre. Et pour chacune des solutions, nous connaissons un gradient qui nous indique comment les paramètres devraient changer si nous voulons encourager ou interdire cette solution dans cet état à l'avenir. Il ne reste plus qu'à étiqueter chaque décision que nous prenons comme bonne ou mauvaise. Par exemple, supposons que nous ayons gagné 12 matchs et perdu 88. Nous prendrons toutes les 200 * 12 = 2400 décisions que nous avons prises dans les jeux gagnants et effectuerons une mise à jour positive (en remplissant un gradient +1,0 pour chaque action, en faisant un backprop et en mettant à jour les paramètres encourageant les actions que nous avons choisies dans toutes ces conditions). Et nous prendrons les 200 * 88 = 17 600 autres décisions que nous avons prises en perdant des jeux et effectuerons une mise à jour négative (n'approuvant pas ce que nous avons fait). Et c'est tout ce qu'il faut. Le réseau sera désormais plus susceptible de répéter des actions qui ont fonctionné et légèrement moins susceptibles de répéter des actions qui n'ont pas fonctionné. Maintenant, nous jouons 100 autres jeux avec notre nouvelle politique légèrement améliorée, puis répétons l'application des dégradés.

Schéma de dessin animé de 4 jeux. Chaque cercle noir est une sorte d'état de jeu (trois exemples d'états sont présentés ci-dessous), et chaque flèche est une transition marquée par l'action qui a été sélectionnée. Dans ce cas, nous avons gagné 2 matchs et perdu 2 matchs. Nous avons pris les deux matchs gagnés et avons légèrement encouragé chaque action que nous avons faite dans cet épisode. Inversement, nous prendrons également les deux matchs perdus et découragerons légèrement chaque action individuelle que nous avons effectuée dans cet épisode.

Si vous réfléchissez à cela, vous commencerez à trouver des propriétés amusantes. Par exemple, que se passe-t-il si nous effectuons une bonne action dans l'image 50, en bottant correctement le ballon, mais que nous ratons ensuite le ballon dans l'image 150? Depuis que nous avons perdu le jeu, chaque action individuelle est maintenant marquée comme mauvaise, et cela n'empêche-t-il pas le coup correct à l'image 50? Vous avez raison - il en sera ainsi pour cette fête. Cependant, lorsque vous considérez le processus dans des milliers / millions de jeux, la bonne exécution du rebond augmente vos chances de gagner à l'avenir. En moyenne, vous verrez des mises à jour plus positives que négatives pour une frappe de raquette appropriée. Et la politique de mise en œuvre du réseau de neurones produira finalement les bonnes réactions.

Mise à jour: le 9 décembre 2016 est une vue alternative. Dans mon explication ci-dessus, j'utilise des termes tels que «définir un gradient et une propagation arrière de backprop», qui est une technique habile définie. Si vous avez l'habitude d'écrire votre propre code back-backprop ou d'utiliser Torch, vous pouvez contrôler entièrement les dégradés. Cependant, si vous êtes habitué à Theano ou TensorFlow, vous serez un peu perplexe car le code backprop est entièrement automatisé et difficile à personnaliser. Dans ce cas, la vue alternative suivante peut être plus productive. En enseignant avec un enseignant, l'objectif habituel est de maximiser

$\ sum_i \ log p (y_i \ mid x_i)$ où

$x_i, y_i$ - des exemples de formation (tels que des images et leurs étiquettes). L'application du gradient à la fonction politique coïncide exactement avec la formation avec l'enseignant, mais avec deux petites différences: 1) nous n'avons pas les bonnes étiquettes

$y_i$ , par conséquent, en tant que «faux label», nous utilisons l'action que nous avons reçue pour sélectionner dans la politique lorsqu'elle a vu

$x_i$ , et 2) Nous introduisons un autre coefficient d'opportunité (avantage) pour chaque action. Ainsi, à la fin, notre perte ressemble maintenant à

$\ sum_i A_i \ log p (y_i \ mid x_i)$ où

$y_i$ - c'est l'action que nous avons réalisée avec l'échantillon, et

$A_i$ Est le nombre que nous appelons le coefficient d'opportunité. Par exemple, dans le cas du pong, la valeur

$A_i$ il pourrait être de 1,0 si nous finissons par gagner l'épisode, et de -1,0 si nous perdons. Cela garantit que nous maximisons la probabilité d'enregistrer des actions qui ont conduit à un bon résultat et minimisons la probabilité d'enregistrer des actions qui ne l'ont pas fait. Et des actions neutres à la suite de nombreux appels n'affecteront pas particulièrement la fonction de la politique. Ainsi, l'apprentissage par renforcement est exactement le même que l'apprentissage avec un enseignant, mais sur un ensemble de données en constante évolution (épisodes), avec un facteur supplémentaire.

Fonctions de faisabilité plus avancées. J'ai également promis un peu plus d'informations. Jusqu'à présent, nous avons évalué l'exactitude de chaque action individuelle selon que nous gagnions ou non. Dans une configuration RL plus générale, nous recevrons une «récompense conditionnelle»

$r_t$ pour chaque étape, en fonction du numéro ou de l'heure. L'une des options courantes consiste à utiliser un coefficient actualisé, de sorte que la «récompense possible» dans le diagramme ci-dessus sera

$R_t = \ sum_ {k = 0} ^ {\ infty} \ gamma ^ k r_ {t + k}$ où

$\ gamma$ Est un nombre de 0 à 1, appelé coefficient d'actualisation (par exemple, 0,99). L'expression dit que la force avec laquelle nous encourageons l'action est la somme pondérée de toutes les récompenses, mais les récompenses suivantes sont exponentiellement moins importantes. Autrement dit, les courtes chaînes d'actions sont mieux encouragées et la queue des longues chaînes d'actions devient moins importante. En pratique, vous devez également les normaliser. Par exemple, supposons que nous calculons

$R_t$ pour l'ensemble des 20 000 actions d'une série de 100 épisodes du jeu. Une très bonne idée est de normaliser ces valeurs (soustraire la moyenne, diviser par l'écart-type) avant de les connecter à l'algorithme backprop. Ainsi, nous encourageons et décourageons toujours environ la moitié des actions effectuées. Cela réduit les fluctuations et rend la politique plus convergente. Une étude plus approfondie est disponible sur [ lien ].

Dérivé d'une fonction de politique. Je voulais également décrire brièvement comment les dégradés sont pris mathématiquement. Les gradients de la fonction de la politique sont un cas particulier d'une théorie plus générale. Le cas général est que lorsque nous avons une expression de la forme

$E_ {x \ sim p (x \ mid \ theta)} [f (x)]$ , c'est-à-dire l'attente d'une fonction scalaire

$f (x)$ avec une certaine distribution de son paramètre

$p (x; \ theta)$ paramétré par un vecteur

$\ theta$ . Alors

$f (x)$ deviendra notre fonction de récompense (ou la fonction d'opportunité dans un sens plus général), et la distribution discrète

$p (x)$ sera notre politique, qui a en fait la forme

$p (a \ mid I)$ donnant les probabilités d'une action a pour l'image

$I$ . Ensuite, nous voulons savoir comment déplacer la distribution de p à travers ses paramètres

$\ theta$ agrandir

$f$ (c'est-à-dire comment modifions-nous les paramètres réseau pour que les actions obtiennent une récompense plus élevée). Nous avons ceci:

$\ begin {align} \ nabla _ {\ theta} E_x [f (x)] & = \ nabla _ {\ theta} \ sum_x p (x) f (x) & \ text {définition de l'attente} \\ & = \ sum_x \ nabla _ {\ theta} p (x) f (x) & \ text {permuter la somme et le gradient} \\ & = \ sum_x p (x) \ frac {\ nabla _ {\ theta} p (x)} {p (x)} f (x) & \ text {multiplier et diviser par} p (x) \\ & = \ sum_x p (x) \ nabla _ {\ theta} \ log p (x) f (x) & \ text {utiliser le fait que} \ nabla _ {\ theta} \ log (z) = \ frac {1} {z} \ nabla _ {\ theta} z \\ & = E_x [f (x) \ nabla _ {\ theta} \ log p (x)] & \ text {définition de l'attente} \ end {align}$

Je vais essayer de l'expliquer. Nous avons une certaine distribution

$p (x; \ theta)$ (J'ai utilisé l'abréviation

$p (x)$ à partir de laquelle nous pouvons sélectionner des valeurs spécifiques. Par exemple, il peut s'agir d'une distribution gaussienne à partir de laquelle un générateur de nombres aléatoires échantillonne. Pour chaque exemple, nous pouvons également calculer la fonction d'estimation

$f$ , qui selon l'exemple actuel nous donne une estimation scalaire. L'équation résultante nous indique comment déplacer la distribution à travers ses paramètres

$\ theta$ si nous voulons d'autres exemples d'actions basées sur elle pour obtenir des taux plus élevés

$f$ . Nous prenons quelques exemples d'actions

$x$ et leur évaluation

$f (x)$ , et aussi pour chaque x, nous évaluons également le deuxième terme

$\ nabla _ {\ theta} \ log p (x; \ theta)$ . Quel est ce multiplicateur? C'est précisément le vecteur - le gradient, qui nous donne une direction dans l'espace des paramètres, ce qui entraînera une augmentation de la probabilité d'une action spécifique

$x$ . En d'autres termes, si nous avons poussé θ dans la direction

$\ nabla _ {\ theta} \ log p (x; \ theta)$ , nous verrions que la nouvelle probabilité de cette action augmentera légèrement. Si vous regardez en arrière la formule, elle nous dit que nous devons prendre cette direction et multiplier la valeur scalaire par elle

$f (x)$ . Cela garantira que les exemples d'actions avec une note plus élevée (dans notre cas, une récompense) «tireront» plus fortement que les exemples avec un indicateur plus bas, donc, si nous devions mettre à jour sur la base de plusieurs échantillons

$p$ , la densité de probabilité se déplacerait vers la direction des points de jeu résultants plus élevés, ce qui augmente la probabilité d'obtenir des exemples d'actions avec des récompenses élevées. Il est important que le gradient ne soit pas pris de la fonction

$f$ , car il peut généralement être indifférencié et imprévisible. Un

$p$ différenciable par

$\ theta$ . C’est

$p$ est une distribution discrète réglable en continu, où vous pouvez ajuster les probabilités d'actions individuelles. Nous supposons également que

$p$ normalisé.

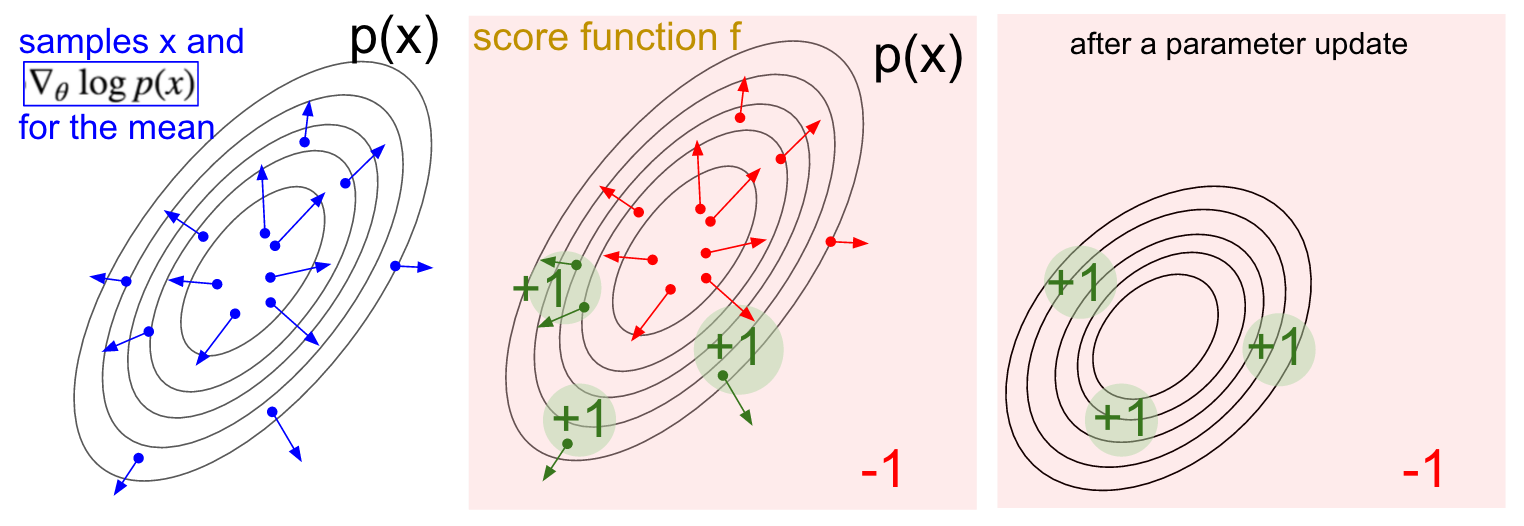Visualisation du dégradé. Gauche: distribution gaussienne et plusieurs exemples de celle-ci (points bleus). À chaque point bleu, nous traçons également le gradient de la probabilité logarithmique par rapport au paramètre moyen. La flèche indique la direction dans laquelle la valeur de distribution moyenne doit être décalée pour augmenter la probabilité de cet exemple d'action. Au milieu: Ajout d'une fonction d'évaluation qui donne -1 partout sauf +1 dans certaines petites régions (notez que cela peut être une fonction scalaire arbitraire et pas nécessairement différentiable). Les flèches sont maintenant codées par couleur, car en raison de la multiplication, nous allons faire la moyenne de toutes les flèches vertes avec une note positive et des flèches rouges négatives. Droite: après la mise à jour des paramètres, les flèches vertes et les flèches rouges inversées nous poussent vers la gauche et vers le bas. Si vous le souhaitez, les échantillons de cette distribution auront désormais une note attendue plus élevée.

J'espère que le lien avec RL est clair.Notre politique nous donne des exemples d'actions, et certaines d'entre elles fonctionnent mieux que d'autres (à en juger par la fonction d'opportunité). La façon de modifier les paramètres de stratégie consiste à exécuter, à prendre le gradient des actions sélectionnées, à le multiplier par la note et à ajouter tout ce que nous avons fait ci-dessus. Pour une conclusion plus approfondie, je recommande une conférence de John Shulman.

La formation. Eh bien, nous avons développé les principes des gradients de la fonction de la politique. J'ai implémenté toute l'approche dans un script Python de 130 lignes qui utilise l'émulateur ATAI 2600 Pong prêt à l'emploi d' OpenAI Gym. J'ai formé un réseau neuronal à deux couches avec 200 neurones à couche cachée en utilisant l'algorithme RMSProp pour une série de 10 épisodes (chaque épisode selon les règles se compose de plusieurs tirages au sort et l'épisode continue de marquer 21). Je n'ai pas trop configuré les paramètres hyper et j'ai expérimenté sur mon Macbook lent, mais après une séance d'entraînement de trois jours, j'ai eu une politique qui joue un peu mieux que le lecteur intégré. Le nombre total d'épisodes était d'environ 8 000, donc l'algorithme a joué environ 200 000 jeux de pong, ce qui est beaucoup, et a produit un total d'environ 800 mises à jour des poids. Si je me suis entraîné sur le GPU avec ConvNets, alors en quelques jours, je pourrais obtenir d'excellents résultats, et si j'optimisais les hyperparamètres, je pourrais toujours gagner. Cependant, je n'ai pas passé trop de temps à calculer ou à configurer,nous avons donc obtenu Pong AI, qui illustre les principales idées et fonctionne assez bien:

.

.Nous pouvons également regarder les poids obtenus du réseau neuronal. Grâce au prétraitement, chacune de nos entrées est une image de différence de 80x80 (image actuelle moins image précédente). Chaque neurone de la couche W1 est connecté à une couche cachée W2 composée de 200 neurones. Le nombre de liaisons est de 80 * 80 * 200. Essayons d'analyser ces connexions. Nous allons trier tous les neurones de la couche W2 et visualiser quels poids y conduisent. À partir des échelles qui mènent à un neurone W2 à partir des neurones W1, nous ferons des images 80x80. Voici 40 images de W2 (un total de 200). Les pixels blancs sont des poids positifs et le noir est négatif. Notez que plusieurs neurones W2 sont réglés sur une boule volante encodée en lignes pointillées. Dans un jeu, la balle ne peut être qu’un seul endroit,par conséquent, ces neurones sont polyvalents et «tireront» si la balle se trouve quelque part à l'intérieur de ces lignes. L'alternance du noir et du blanc est intéressante, car lorsque la balle se déplace le long de la piste, l'activité du neurone fluctue comme une onde sinusoïdale. Et à cause de ReLU, il ne «tirera» que sur certaines positions. Il y a beaucoup de bruit dans les images, ce qui serait moins si j'utilisais la régularisation L2.

Ce qui ne se passe pas. Nous avons donc appris à jouer au pong sur des images en utilisant le gradient de la fonction de stratégie, et cela fonctionne plutôt bien. Cette approche est une forme bizarre de «suggestion et vérification», où «deviner» fait référence à l'exécution de notre politique sur plusieurs épisodes du jeu, et la «vérification» encourage les actions qui mènent à de bons résultats. En général, cela représente le niveau actuel de la façon dont nous abordons actuellement les problèmes de l'apprentissage renforcé. Si vous comprenez l'algorithme intuitivement et savez comment il fonctionne, vous devriez être au moins un peu déçu. En particulier, quand ça ne marche pas?

Comparez cela à la façon dont une personne peut apprendre à jouer au pong. Vous leur montrez vous-même le jeu et dites quelque chose comme: "Vous contrôlez la raquette, vous pouvez la déplacer de haut en bas, et votre tâche est de lancer la balle devant un autre joueur contrôlé par le programme intégré", et vous êtes prêt à partir. Veuillez noter quelques différences:

- , , , . RL , . , ( ), , . . , , , , , , , , .
, ( , , , ..), ( «» « , , , - - . .). «» / . , , ( ) ( , ).
— (brute force), , . . , , , . , «» , . , , .
, , . , , . .

: : RL. , , . , . , 99% . , «» . : «», , - , - , - , , . « , ».

Je voudrais également souligner le fait qu'au contraire, dans de nombreux jeux, les gradients de la politique vaincraient facilement une personne. En particulier, cela s'applique aux jeux avec des récompenses fréquentes, qui nécessitent une réaction précise et rapide et sans planification à long terme. Les corrélations à court terme entre les récompenses et les actions sont facilement visibles par l'approche PG. Vous pouvez voir similaire dans notre agent Pong. Il développe une stratégie lorsqu'il attend simplement le ballon, puis se déplace rapidement pour l'attraper uniquement au bord même, c'est pourquoi le ballon rebondit à une vitesse verticale élevée. L'agent gagne plusieurs victoires d'affilée, répétant cette stratégie simple. Il existe de nombreux jeux (Pinball, Breakout) dans lesquels Deep Q-Learning attire et piétine une personne dans la boue avec ses actions simples et précises.

Une fois que vous avez compris le «truc» avec lequel ces algorithmes fonctionnent, vous pouvez comprendre leurs forces et leurs faiblesses. En particulier, ces algorithmes sont loin derrière les gens dans la construction d'idées abstraites sur les jeux que les gens peuvent utiliser pour un apprentissage rapide. Une fois que l'ordinateur a regardé le tableau de pixels et a remarqué la clé, la porte se dit qu'il serait probablement bien de prendre la clé et de se rendre à la porte. Il n'y a actuellement rien de semblable à cela, et essayer d'y arriver est un domaine de recherche actif.

Calculs non différenciables dans les réseaux de neurones.Je voudrais mentionner une autre application intéressante des gradients de politique non liés au jeu: cela nous permet de concevoir et d'entraîner des réseaux de neurones en utilisant des composants qui fonctionnent (ou interagissent) avec des calculs non différenciables. Cette idée a été introduite pour la première fois en 1992 par Williams . et a récemment été popularisé dans les modèles récurrents d'attention visuelle.appelé «attention particulière» dans le contexte d'un modèle qui traite une image avec une séquence d'apparences fovéales étroites à basse résolution, semblable à la façon dont notre œil examine les objets avec une vision centrale en cours d'exécution. À chaque itération, le RNN recevra un petit fragment de l'image et sélectionnera l'emplacement à rechercher plus loin. Par exemple, le RNN peut regarder la position (5.30), obtenir un petit fragment de l'image, puis décider de regarder (24, 50), etc. Il y a une section du réseau neuronal qui sélectionne où regarder plus loin, puis l'inspecte. Malheureusement, cette opération n'est pas différenciable, car nous ne savons pas ce qui se passerait si nous prélevions un échantillon ailleurs. Dans un cas plus général, considérons un réseau neuronal qui a plusieurs entrées et sorties:

Notez que la plupart des flèches bleues sont différenciables comme d'habitude, mais certaines transformations de vue peuvent également inclure une opération de sélection indifférenciée, qui sont surlignées en rouge. Nous pouvons simplement parcourir les flèches bleues dans la direction opposée, mais la flèche rouge est une dépendance à travers laquelle nous ne pouvons pas inverser la propagation du backprop.

Une politique de dégradé à la rescousse! Réfléchissons à la partie du réseau qui effectue l'échantillonnage et peut être représentée en fonction de la politique stochastique intégrée dans un grand réseau de neurones. Par conséquent, pendant la formation, nous produirons plusieurs exemples (indiqués par les branches ci-dessous), puis nous encouragerons les échantillons qui conduisent finalement à de bons résultats (dans ce cas, par exemple, mesurés par la perte à la fin). En d'autres termes, nous formerons les paramètres inclus dans les flèches bleues en utilisant le backprop, comme d'habitude, mais les paramètres inclus dans la flèche rouge seront désormais mis à jour indépendamment du passage inverse en utilisant des gradients de politique, encourageant les échantillons qui entraînent de faibles pertes. Cette idée a également été récemment bien cadrée.Estimation du gradient à l'aide de graphiques de calcul stochastiques.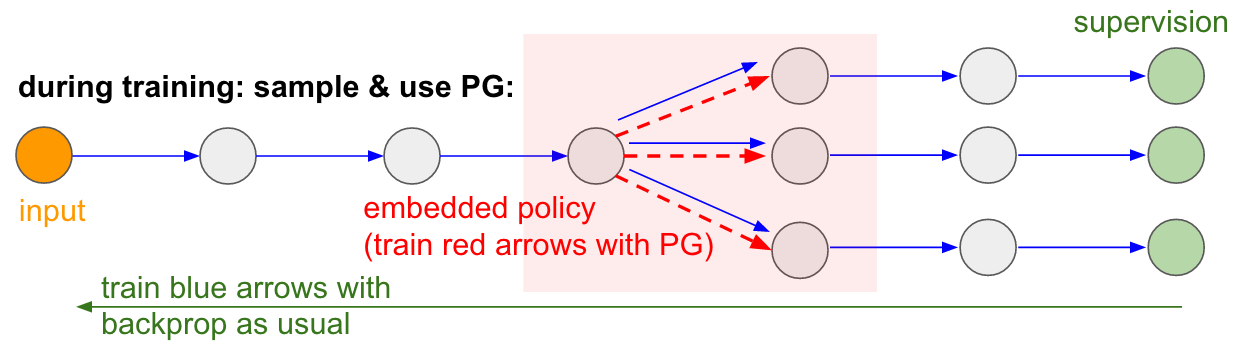

Entrée / sortie formée dans la mémoire à accès aléatoire. Vous retrouverez également cette idée dans de nombreux autres articles. Par exemple, la Neural Turing Machine a une bande mémoire avec laquelle ils lisent et écrivent. Pour effectuer une opération d'écriture, vous devez faire quelque chose comme m [i] = x, où i et x sont prédits par le réseau neuronal RNN. Cependant, aucun signal ne nous dit ce qui arriverait à la fonction de perte si nous écrivions j! = I. Par conséquent, NTM peut effectuer des opérations de lecture et d'écriture en douceur. Il prédit la fonction de distribution d'attention a, puis effectue pour tout i: m [i] = a [i] * x. Il est désormais différenciable, mais nous devons payer un prix de calcul élevé, en triant toutes les cellules.

Cependant, nous pouvons utiliser des gradients de politique pour contourner théoriquement ce problème, comme cela est fait dans RL-NTM. Nous prédisons toujours la distribution de l'attention a, mais au lieu d'une recherche exhaustive, nous sélectionnons au hasard des lieux d'écriture: i = échantillon (a); m [i] = x. Pendant la formation, nous pourrions le faire pour un petit ensemble de i et, à la fin, trouverions un ensemble qui fonctionnerait mieux que les autres. Un grand avantage de calcul est que pendant les tests, vous pouvez lire / écrire à partir d'une cellule. Cependant, comme indiqué dans le document, cette stratégie est très difficile à mettre en œuvre, car vous devez passer par de nombreuses options et passer presque accidentellement à des algorithmes de travail. Actuellement, les chercheurs conviennent que PG ne fonctionne bien que lorsqu'il existe plusieurs options discrètes, lorsque vous n'avez pas besoin de passer au peigne fin les grands espaces de recherche.

Cependant, à l'aide de gradients politiques et dans les cas où une grande quantité de données et de puissance de calcul est disponible, nous pouvons en principe rêver beaucoup. Par exemple, nous pouvons concevoir des réseaux de neurones qui apprennent à interagir avec de grands objets non différenciables, tels que des compilateurs en latex. Par exemple, pour que char-rnn génère du code Latex prêt à l'emploi, ou un système SLAM, ou des solveurs LQR, ou autre chose. Ou, par exemple, la superintelligence peut vouloir apprendre à interagir avec Internet via TCP / IP (qui n'est pas non plus différenciable) pour accéder aux informations nécessaires pour capturer le monde. Ceci est un excellent exemple.

Conclusions

Nous avons vu que les gradients de politique sont un puissant algorithme général, et à titre d'exemple, nous avons formé l'agent ATARI Pong à partir de pixels bruts à partir de zéro dans 130 lignes Python . En général, le même algorithme peut être utilisé pour former des agents à des jeux arbitraires et, espérons-le, un jour nous pourrons l'utiliser pour résoudre des problèmes de contrôle dans le monde réel. En conclusion, je voudrais ajouter quelques commentaires:

sur le développement de l'IA. Nous avons vu que l'algorithme fonctionne au moyen de la recherche par force brute, dans laquelle vous hésitez d'abord au hasard et devez tomber sur des situations utiles au moins une fois, et idéalement souvent, avant que la fonction de politique modifie ses paramètres. Nous avons également vu qu'une personne aborde ces solutions à ces problèmes d'une manière complètement différente, ce qui ressemble à la construction rapide d'un modèle abstrait. Étant donné que ces modèles abstraits sont très difficiles (voire impossibles) à imaginer explicitement, c'est aussi la raison pour laquelle il y a récemment eu un tel intérêt pour les modèles génératifs et l'induction de logiciels.

À propos de l'utilisation en robotique.L'algorithme ne s'applique pas lorsqu'il est difficile d'obtenir une énorme quantité de recherches. Par exemple, vous pouvez avoir un (ou plusieurs) robots interagissant avec le monde en temps réel. Cela ne suffit pas pour une application naïve de l'algorithme. Un domaine de travail conçu pour atténuer ce problème est celui des gradients politiques déterministes . Au lieu de faire de véritables tentatives, cette approche obtient des informations de gradient à partir d'un deuxième réseau neuronal (appelé critique) qui modélise la fonction d'évaluation. Cette approche peut, en principe, être efficace avec des actions de grande dimension, où l'échantillonnage aléatoire offre une faible couverture. Une autre approche connexe consiste à intensifier la robotique que nous commençons à voir sur Google Robot Farmou peut-être même sur une Tesla S + avec pilote automatique.

Il existe également une ligne de travail qui essaie de rendre le processus de recherche moins désespéré en ajoutant un contrôle supplémentaire. Par exemple, dans de nombreux cas pratiques, vous pouvez obtenir la direction initiale du développement directement de la personne. Par exemple, AlphaGo utilise d'abord la formation avec un enseignant pour prédire uniquement les actions humaines (par exemple, le contrôle à distance du robot , l' apprentissage , l' optimisation de la trajectoire , la recherche de politique complète ). Et la politique résultante est ensuite configurée à l'aide de PG pour atteindre le véritable objectif - gagner le match.

Dans certains cas, il peut y avoir moins de préréglages (par exemple, pour contrôler à distance des robots ), et des méthodes existent pour utiliser ces données de pré-stage . Enfin, si les gens ne fournissent pas de données ou de paramètres spécifiques, ils peuvent également être obtenus dans certains cas par calcul en utilisant des méthodes d'optimisation assez coûteuses, par exemple, en optimisant la trajectoire dans un modèle dynamique connu (comme F = ma dans un simulateur physique) ou dans des cas lorsqu'un modèle local approximatif est créé (comme le montre une structure très prometteuse pour la recherche de politique gérée).

À propos de l'utilisation de PG dans la pratique.Je voudrais parler davantage de RNN. Je pense qu'il peut sembler que les RNN sont magiques et résolvent automatiquement les problèmes liés aux séquences arbitraires. La vérité est que faire fonctionner ces modèles peut être délicat. Des soins et de l'expérience sont nécessaires, ainsi que de savoir quand des méthodes plus simples peuvent vous aider à 90%. Il en va de même pour les gradients politiques. Ils ne fonctionnent pas automatiquement comme ça: vous avez besoin de nombreux exemples, ils peuvent s'entraîner indéfiniment, ils sont difficiles à déboguer quand ils ne fonctionnent pas. Vous devez toujours essayer de tirer avec un petit pistolet avant d'atteindre Bazooka. Par exemple, dans le cas d'un entraînement par renforcement, la méthode de l'entropie croisée (CEM) doit toujours être vérifiée en premier., une approche stochastique simple «deviner et vérifier» inspirée de l'évolution. Et si vous insistez pour essayer des gradients de stratégie pour votre tâche, assurez-vous de connaître les astuces spécifiques. Commencez simplement et utilisez une option PG appelée TRPO , qui fonctionne presque toujours mieux et de manière plus cohérente que la PG classique . L'idée de base est d'éviter de mettre à jour les paramètres qui modifient trop votre politique, en raison de l'utilisation de la distance Kulbak-Leibler entre l'ancienne et la nouvelle politique.

C’est tout!J'espère que je vous ai donné une idée de l'endroit où nous en sommes avec l'apprentissage par renforcement, quels sont les problèmes, et si vous voulez aider à promouvoir RL, je vous invite à le faire dans notre OpenAI Gym :) A la prochaine fois!

Andrej Karpathy,
chercheur, développeur, directeur du département d'IA et pilote automatique Tesla

Informations supplémentaires:

Deep Learning on Fingers Course 2018
https://habr.com/en/post/414165/ Deep Learning on Fingers

Open Course 2019
https: // habr.com/ru/company/ods/blog/438940/

Faculté de physique de NSU
http://www.phys.nsu.ru/

Renforcement de l'apprentissage en profondeur: ping pong pixel brut

Conclusions

More articles: